高考中常見的含輕彈簧的題型剖析
陳維波
(山東省沂南第一中學)
彈簧作為物理學習中常見的研究對象,在高中階段是一個非常重要的考查類型——輕彈簧模型.含有輕彈簧的題目在高考中時常出現,有必要對其進行總結分析,以提高學生的解題能力.
在高中階段,很多研究內容都被“理想化”了,比如質點、輕桿、滑輪、理想氣體等,輕彈簧也是一個理想化模型.它是一個不計自身重力、各處受力相等、彈力嚴格滿足胡克定律、不受運動狀態影響的理想化物理模型.
如圖1所示,同一根輕彈簧處在四種不同情況下:甲圖中輕彈簧左端固定;乙圖中輕彈簧左右兩端均自由;丙圖中輕彈簧左端與一質量為m的物塊連接且物塊放在光滑水平面上;丁圖中輕彈簧左端與一質量為m的物塊連接且物塊放在粗糙水平面上.除此之外,輕彈簧的自由端都受到一個水平恒力F的作用.根據輕彈簧的性質,我們知道四幅圖中輕彈簧伸長量的關系為Δl甲=Δl乙=Δl丙=Δl丁.
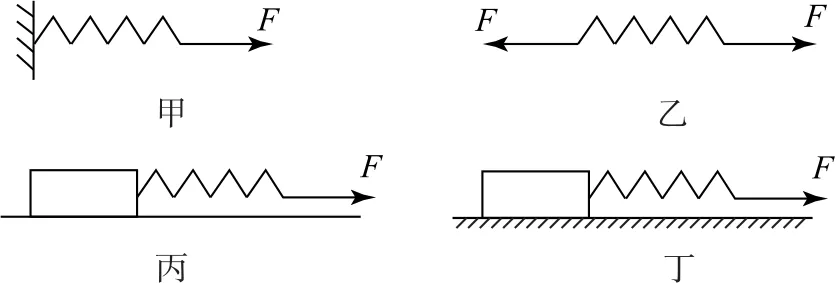
圖1
以上簡單回顧了輕彈簧的性質,接下來再看一下在高中物理學習過程中涉及輕彈簧的兩種常見題型.
1 靜力學問題常見題型
靜力學問題是最基礎、最簡單也是最常見的題型,主要考查力的平衡問題,解題的關鍵是正確進行受力分析,確定輕彈簧對研究對象的彈力,然后利用平衡條件列方程求解.
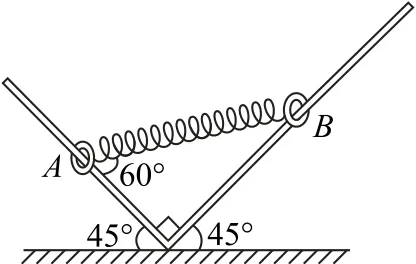
圖2
(1)輕彈簧的原長;
(2)金屬環B與細桿間的動摩擦因數.
(1)如圖3所示,對金屬環A受力分析,由幾何知識可得,解得.
設彈簧的壓縮量為Δx,則有FT=kΔx,解得.所以輕彈簧的原長為
(2)對金屬環B受力分析如圖3所示,因為其處于平衡狀態,則由平衡條件,對沿右側細桿方向可得
沿垂直細桿方向可得
【小結】在靜力學問題中,彈簧的存在主要是提供彈力,解題的關鍵是正確判斷彈力的方向,需具備的知識儲備包括受力分析、力的合成與分解、胡克定律和幾何知識.解題思路可歸納為:
第一步:確定研究對象,判斷彈簧的狀態,進而確定彈力的大小和方向.第二步:對研究對象進行受力分析,由于輕彈簧是理想模型,所以彈力的方向必然在彈簧所在的直線上.第三步:根據力的平衡條件列方程求解.
2 動力學問題常見題型
在動力學問題中涉及輕彈簧時,最常遇到的有三種情況:一是瞬時問題,即由于彈簧形變恢復需要時間,在輕彈簧受力發生變化內瞬間其形變未改變,可認為輕彈簧的彈力不變;二是在圓周運動中,彈簧不能視為輕繩,而是類似輕桿,但由于輕彈簧會被壓縮,所以將其視為長度可變化的輕桿更合適;三是臨界條件問題,輕彈簧不與研究對象連接時,臨界條件就是輕彈簧恢復原長時對研究對象無彈力作用.
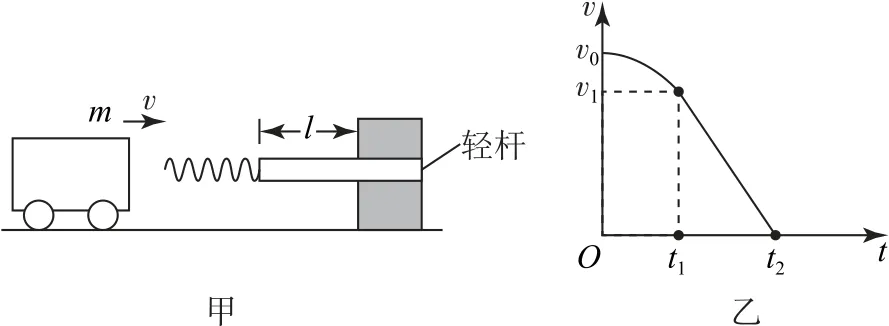
圖4
A.小車在0~t1時間內的位移為
B.小車在時刻t1的速度為
C.輕桿在0~t2時間內由摩擦產生的熱量為fl
D.在t1+t2時刻小車恰好與輕彈簧分離
想要輕桿向右移動,則需要彈簧的彈力達到輕桿與固定槽之間的摩擦力,則有f=kx,在彈簧從初始狀態到被壓縮x長度后,到小車速度與輕桿速度相等,此時彈簧的壓縮量達到最大值;隨后輕桿、輕彈簧和小車組成的系統開始不斷減速,直到靜止;之后是小車在彈簧彈力作用下向左做加速運動.0~t1時間代表從彈簧剛開始被壓縮到輕桿恰好開始運動的時間段,因此,該時間段內小車的位移即輕彈簧的壓縮量,即,則可知選項A 錯誤.在0~t1時間內,輕彈簧彈力做功可以用平均力求解,由上面分析可知t1時刻彈簧彈力為f,對小車應用動能定理可得,解得,所以選項B錯誤.
輕桿在0~t2時間內相對固定槽的位移為l,故該過程中因為摩擦產生的熱量為Q=fl,所以選項C正確.
在0~t1時間內,小車做加速度增大的減速運動.在t1~t2時間內,小車、彈簧與輕桿一起做勻減速運動.最后小車被反彈做加速度減小的加速運動,此過程輕桿靜止不動.結合平均速度分析可知小車從開始被反彈向左運動到與彈簧分離所用時間要大于t1,因此,在t1+t2時刻小車與彈簧還未分離,所以選項D錯誤.
【小結】在動力學問題中,分析彈簧與研究對象的關系及特殊時刻彈簧所處狀態是關鍵.解題時,分析彈力和加速度的關系常用牛頓第二定律、胡克定律;分析速度、位移與加速度的關系常用運動學公式.其實,輕彈簧的加入,只是為動力學問題增加了一個力的變量,解題的整體思路并沒有改變.
輕彈簧作為物理研究中的常見對象,以它為組成部分的題目并不限于以上類型,連接體問題、簡諧運動問題、圓周運動問題、電磁感應問題等題目,也常有它的身影,我們不妨多總結歸納,必會對學習有所幫助.
(完)

