對兩道繩、桿連接體問題的深入研究
黃尚鵬
(湖北省監利市實驗高級中學)
本文先對一道繩連接體問題運用兩種方法尋找系統總動能最大時的位置,闡釋“保守力學體系在系統的平衡位置勢能取極值”這一結論;再對2015年高考全國Ⅱ卷一道桿連接體問題進行定量研究,求出滑塊的最大速度和最大加速度以及桿對滑塊的作用力隨桿與豎直方向的夾角的變化規律,并為本題的定性解答提供理論依據,以體現高考命題的科學性.
1 繩連接體問題的深入研究
1.1 對原題的分析與解答
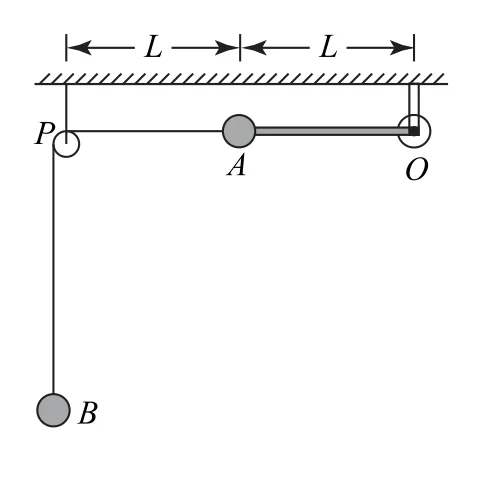
圖1
方法1 矢量三角形法
如圖2所示,假設小球A在A'位置時,A、B組成的系統靜止,此時輕桿與水平方向成θ角,A'P段的輕繩與水平方向成α角.對小球A、B進行受力分析,小球B受力平衡,輕繩的拉力FT=mg,小球A受重力2mg、輕桿的彈力FN和輕繩的拉力FT的作用,且這三個力平衡,構成一個封閉的矢量三角形.在矢量三角形中,由正弦定理得
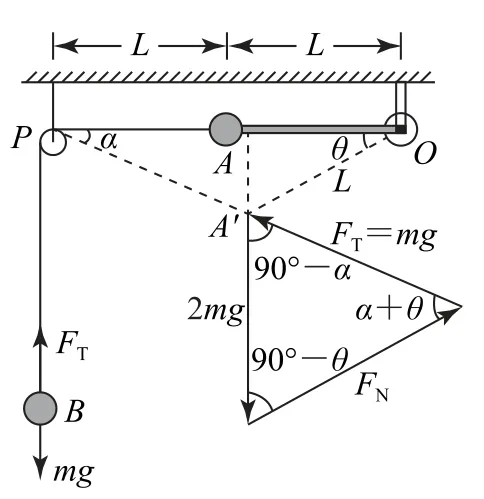
圖2
聯立式①②,得sinα=cosθ,故α+θ=90°,此時輕繩與輕桿夾角為90°.
將α+θ=90°代入式①,得,故此時輕桿與水平方向的夾角θ=60°.
方法2 正交分解法
如圖3所示,對小球A受力分析,由平衡條件得水平方向:豎直方向:
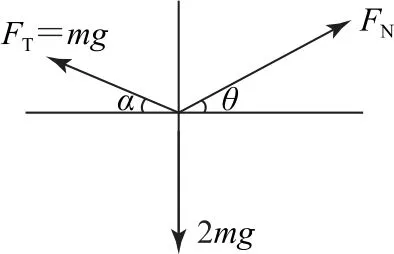
圖3
2)尋找系統總動能最大時的位置.
如圖4所示,假設小球A運動到A'位置時,輕桿與水平方向成θ角,A'P段的輕繩與水平方向成α角.由機械能守恒定律可知,當系統的總動能最大時,系統的總勢能最小,系統勢能減少最多,下面我們用兩種方法尋找系統總動能最大時的位置.
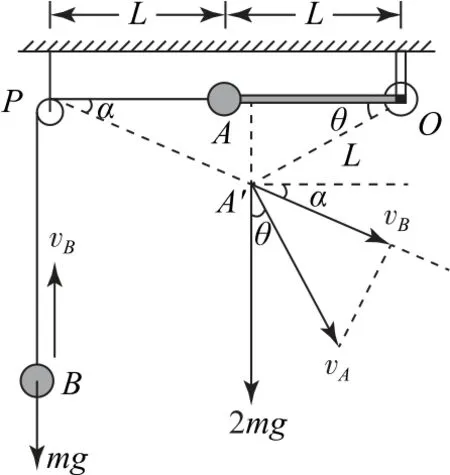
圖4
方法1 數學方法
在△POA'中,由余弦定理得
故當輕桿與水平方向的夾角θ=60°時,即在系統靜止時的平衡位置,A、B組成的系統總動能最大.
方法2 物理方法
根據重力做功與重力勢能變化的關系WG=-ΔEp可知,當系統的重力做正功時,系統的重力勢能減少,當系統的重力做負功時,系統的重力勢能增加,故當系統的重力總功率為零時,系統勢能取極值.或者對系統應用動能定理W合=ΔEk,當系統的合外力做功最多時,系統的總動能增加最多,故當系統的重力總功率為零時,系統的總動能最大.設此時小球A的速度為vA(vA與輕桿垂直),小球B的速度為vB,則
聯立式①②③,得sinα=cosθ,故α+θ=90°,此時輕繩與輕桿夾角為90°,即在系統靜止時的平衡位置,A、B組成的系統總動能最大.
1.2 總結
1)本題要尋找系統總動能最大時的位置,常規思路是根據機械能守恒定律得出系統總動能的表達式,然后利用數學工具求極值,考查利用數學知識解決物理問題的能力.方法1以θ為自變量,利用導數工具,根據復合函數的導數公式求解,由一階導數為零求出極值出現的位置.方法2是物理解法,根據“系統的重力總功率為零時系統的總動能最大”這一條件巧解,屬于特殊快捷解法,要求考生具有敏銳的洞察力,一般考生難以想到.
2)本題得出系統在靜止時的平衡位置總動能最大,這是一種巧合還是必然呢? 其實理論力學中根據分析力學原理可得出這樣一個基本結論:保守力學體系在系統的平衡位置勢能取極值,本題就是根據這一結論改編而成的.為進一步理解這一思想,筆者再舉一個典型例子.如圖5所示,半徑為r的光滑半球形碗O固定在水平面上,一長度為l、質量為m的均質棒斜靠在碗緣,一端A在碗內,另一端B在碗外,棒靜止時與水平方向的夾角為α,試證明:
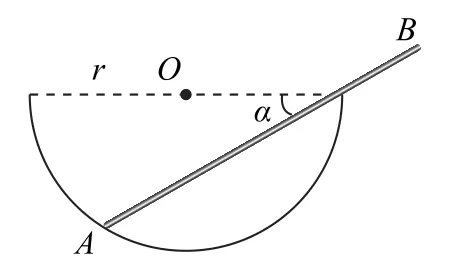
圖5
我們知道如果一個力所做的功與具體路徑無關,這種力叫作保守力.在保守力場中,保守力所做的功等于勢能的減少.保守力學體系處于平衡狀態時勢能取極值,根據系統勢函數一階導數為零,可得出系統在保守力以及約束力等作用下的平衡位置,因此此平衡問題也可用能量的觀點求解.如圖6所示,選碗口所在的水平面為重力勢能參考面,則棒的勢函數
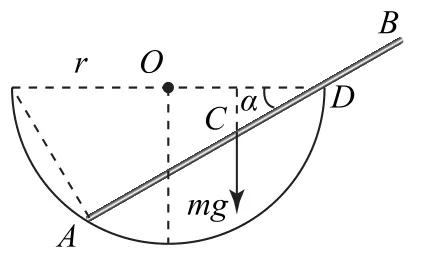
圖6
以α為自變量,對勢函數求一階導數,并令導數為零,尋找平衡位置,即
為驗證上述解法是否正確,嘗試用其他觀點求解本題.如圖7所示,對棒進行受力分析,由三力匯交原理知,彈力FN1、彈力FN2和重力mg的作用線相交于一點E.由幾何關系得lOA=lOD=lOE=r,∠DOE=2α,∠AEC=90°-2α,∠ACE=90°+α.在△ACE中,由正弦定理得所以有
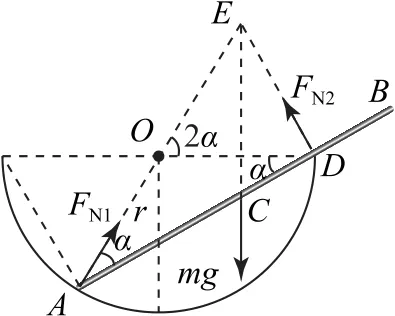
圖7
2 桿連接體問題的深入研究
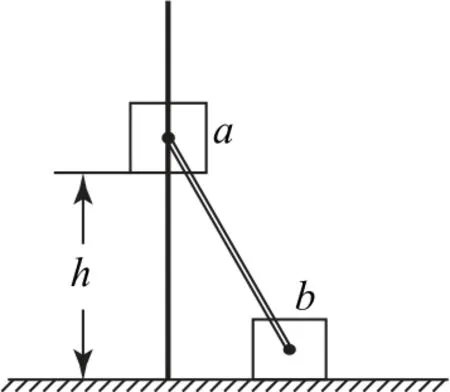
圖8
A.a落地前,輕桿對b一直做正功
B.a落地時速度大小為
C.a下落過程中,其加速度大小始終不大于g
D.a落地前,當a的機械能最小時,b對地面的壓力大小為mg
2.1 滑塊a 落地前,滑塊b 的最大速度
為方便起見,我們假設初始時刻輕桿沿豎直方向,桿長為L,由于受到輕微擾動,整個系統由靜止開始運動.
如圖9所示,設某時刻滑塊a、b的速度分別為va、vb,此時刻桿與豎直方向的夾角為θ,根據兩滑塊沿桿方向的分速度相等得
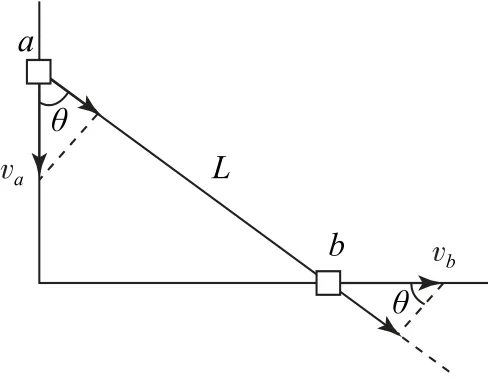
圖9
由系統機械能守恒,得
2.2 滑塊a 落地前,滑塊a 的最大加速度
如圖10所示,由速度矢量三角形得滑塊b相對滑塊a的速度與兩滑塊的速度大小關系為
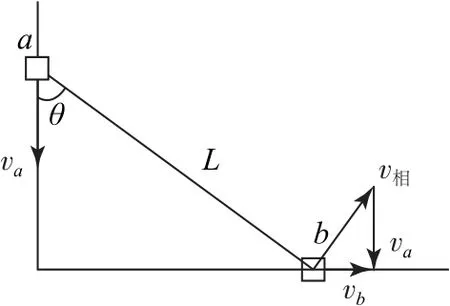
圖10
滑塊a的a0-cosθ圖像是拋物線的一部分,如圖11所示,其中當cosθ=2 3時,滑塊a的加速度a0=g,這是不難理解的,因為由前面的分析可知,此時b的速度最大,b的加速度為零,桿對兩滑塊的作用力F=0.
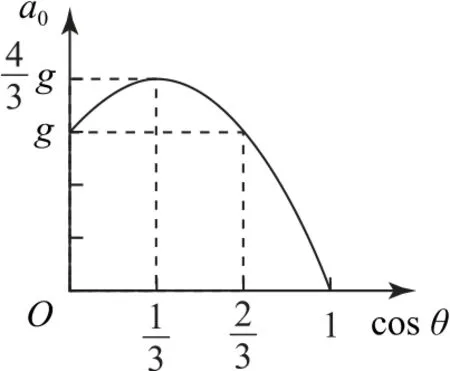
圖11
2.3 滑塊a 落地前,桿對滑塊的作用力F 隨桿與豎直方向的夾角θ 的變化規律
如圖12所示,設桿對兩滑塊的作用力為F(下面我們約定用正值表示推力,負值表示拉力),對兩滑塊受力分析,設地面對滑塊b的支持力為FN,在地面參考系中,滑塊b在豎直方向處于靜止,由平衡條件得
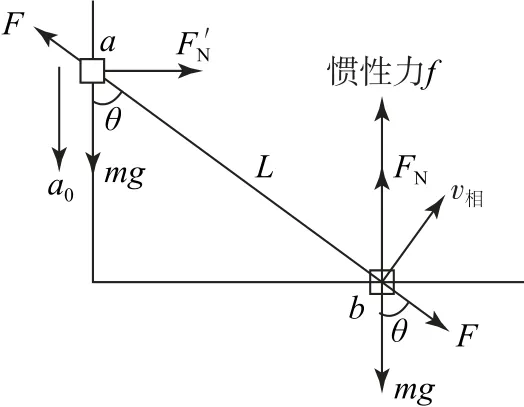
圖12
選滑塊a為參照系(非慣性系),研究滑塊b相對滑塊a的運動,為使牛頓運動定律成立,必須引入慣性力,慣性力的大小
滑塊b相對滑塊a做圓周運動,向心力為指向圓心的合力
3)滑塊a的加速度大小,化簡得a0=(-3cos2θ+2cosθ+1)g,這與前面得出的結論完全一致.
(完)

