基于隨機森林算法的電氣設備異常振動識別方法

周弘毅，夏 磊

（國電南瑞科技股份有限公司，江蘇 南京）

引言

隨著電力系統的發展，電氣設備的容量也不斷增加。電氣設備的安全關系到電力系統的平穩性。為了避免電氣設備的故障問題，研究人員從設備異常振動方面著手，設計了相關的設備異常振動識別方法。其中，基于EMD-LS-MFDFA 法的異常振動識別方法利用經驗模態分解的方式，將設備異常振動信號提取出來，再結合最小二乘法對振動信號特征進行優化擬合，最后使用多重分形去趨勢波動分析法分析設備異常振動信號[1]。基于此，結合EMD、LS、MFDFA 等方法，將異常振動信號以特征參數的形式呈現，從而減少振動識別誤差。基于遷移學習的設備異常振動識別方法利用遷移學習，對復雜環境下的設備異常振動情況進行精準識別，從而優化差異性正則化損失函數，獲得更加有效的識別模型[2]。

然而，以上兩種方法易受到異常諧波的影響，導致識別結果存在一定的隨機誤差。因此，本文利用隨機森林算法，設計了新的電氣設備異常振動識別方法。

1 電氣設備異常振動隨機森林識別方法設計

1.1 提取電氣設備異常振動諧波特征

諧波是電氣設備異常振動中非周期性波形，諧波電流是正常振動電流的整數倍。對于電氣設備而言，異常振動諧波包括分數諧波、間諧波、次諧波，只有將所有異常振動諧波特征均提取出來，才能對電氣設備的非線性諧波分量進行分析，確定電氣設備異常振動的類型[3]。在電氣設備的固定設備中，諧波是非線性產生的，利用波形控制找出異常振動諧波發生源。本文將異常振動諧波設定為i(θ ) ，交流失真波為 ω。假設ω =θ，則異常振動諧波表示為：

式（1）中，i(ω ) 為交流失真波的特征分量；2 π為交流失真波的諧波周期。在電氣設備異常振動的狀態下，流過電氣線路的 ω 為 -i(θ )的對稱波，并且出現i(- θ ) =-i( θ)的奇次諧波[4]。奇次諧波電流波形特征如圖1 所示。

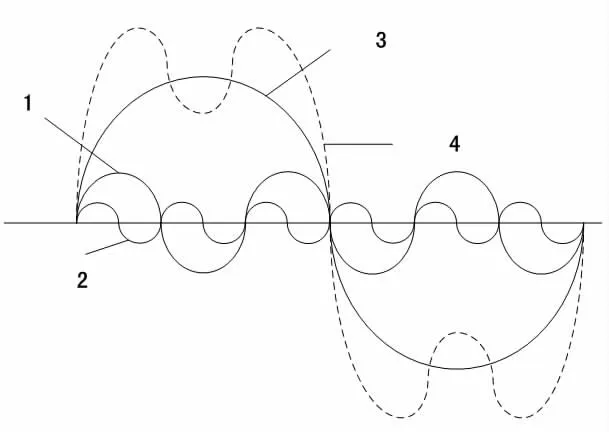
圖1 奇次諧波電流波形特征

圖1 中，1、2、3、4 分別為3 次諧波、5 次諧波、基礎波、合成波。在電氣線路中所發生的奇次諧波中，異常諧波就會產生沖擊脈沖，根據沖擊脈沖的大小，判定電氣設備的應力老化類型。再結合異常振動諧波特征，確定電氣設備熱異常、電壓應力異常、機械應力異常、環境應力異常、復合應力異常等異常振動類別，從而其進行針對性的振動識別。

1.2 基于隨機森林算法構建電氣設備異常振動識別模型

電氣設備異常振動信號間斷性，是產生異常振動混疊噪聲的主要原因。在異常振動諧波特征提取之后，存在正常諧波混雜的問題，影響電氣設備異常振動識別效果[5]。本文利用隨機森林算法，構建出電氣設備異常振動識別模型。通過隨機生成的白噪聲序列，消除電氣設備異常振動區域的混疊噪聲，并將異常振動數據進行相關性變量識別，避免過擬合的問題。隨機生成的白噪聲序列為ni(t)，得到：

式（2）中，wi,k(t)為第i 個白噪聲的第k 階IMF分量；r′(t)為第i 個白噪聲的殘余分量。在電氣設備異常振動識別的過程中，本文以決策樹作為識別模型，從樹的根節點出發，每一個節點在最優的異常特征處分裂，進而逐個節點構建一個樹，直到滿足諧波/基波為全部異常狀態的條件，完成決策樹的異常識別。隨機森林決策樹識別模型如圖2 所示。

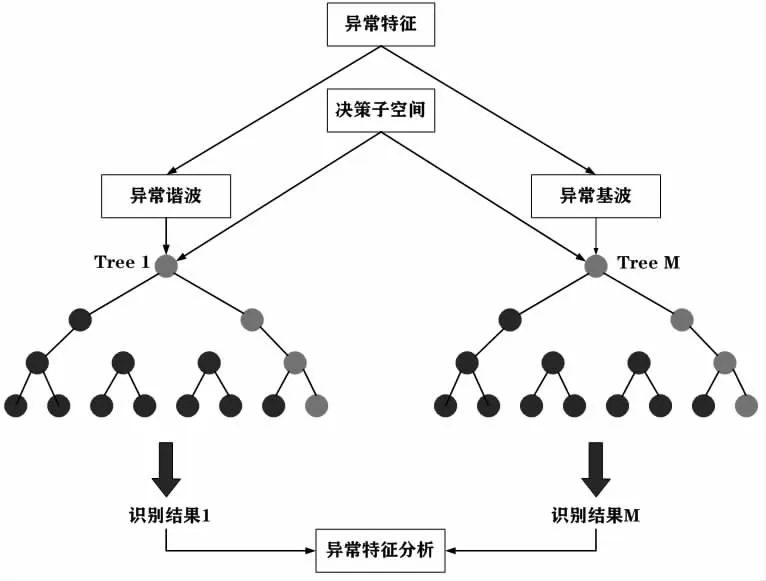
圖2 隨機森林識別模型

圖2 中，在Tree 1 中，灰色圓點為正常諧波；黑色圓點為異常諧波；在Tree M 中，灰色圓點為正常基波，黑色圓點為異常基波。本文將異常諧波與異常基波在隨機森林決策樹上進行識別，在Tree 1 中識別異常諧波中的正常諧波；在Tree M 中識別異常基波中的正常基波。將異常諧波與異常基波中的正常諧波、基波排除之后，得到的識別結果1 與識別結果M 就是最為準確的電氣設備異常振動數據。在異常特征分析的過程中，本文利用識別信度指標，衡量識別結果的可靠性。信度公式為：

1.3 識別電氣設備劣化異常狀態

在識別模型得到電氣設備異常振動識別結果之后，本文根據識別結果，判斷電氣設備的劣化等級，為電氣設備提供針對性的運維決策。電氣設備劣化等級劃分情況如表1 所示。

表1 劣化等級劃分

表1 中，經過異常振動識別之后，將存在異常的B1、B2、B3、C 設備進行實時關注，在劣化等級為C 的設備上關注度增加，秉持著“早發現，早治療”的觀念，保持電氣設備的長久運行。

2 實驗與分析

為了驗證本文方法的有效性，設計如下實驗，并將文獻[1]方法、文獻[2]方法作為對比。

2.1 實驗過程

本次實驗將風機齒輪箱的電氣設備作為異常振動識別目標，通過現場采集的數據，識別該設備的異常振動情況。風機齒輪箱2.0 MW，風機齒輪箱為一級行星太陽輪&一級行星輪，二級太陽輪&平行級中間軸結構，齒輪傳動比為131.58，齒輪箱型號為FD2250MD。

在齒輪箱上布置一個振動傳感器，傳感器在主軸承徑向、軸向；齒輪箱徑向；發電機徑向等位置布置監測點，找出發電設備的異常振動問題。根據振動傳感器傳回的數據得知，主軸承上存在8 個異常振動點位，分別為主軸承徑向與軸向的12 點、3 點、6 點、9 點鐘方向的異常振動；齒輪箱徑向1 點、5 點、7 點、11 點鐘方向的異常振動；發電機徑向12 點、3 點、6 點、9 點鐘方向的異常振動。本文將振動傳感器采集的異常振動數據進行分析，并計算出發電設備各個零部件異常振動的均方根誤差，過程如下：

2.2 實驗結果

在上述實驗條件下，本文隨機選取出主軸承、齒輪箱、發電機等電氣設備，對其異常振動位置進行識別。識別信度是對異常振動識別數據的可靠性驗證結果，識別信度越高，振動數據識別的隨機誤差越小。RMSE 值是異常振動識別的均方根誤差值，RMSE 值越小，振動數據識別的準確性越高。實驗結果如表2所示。

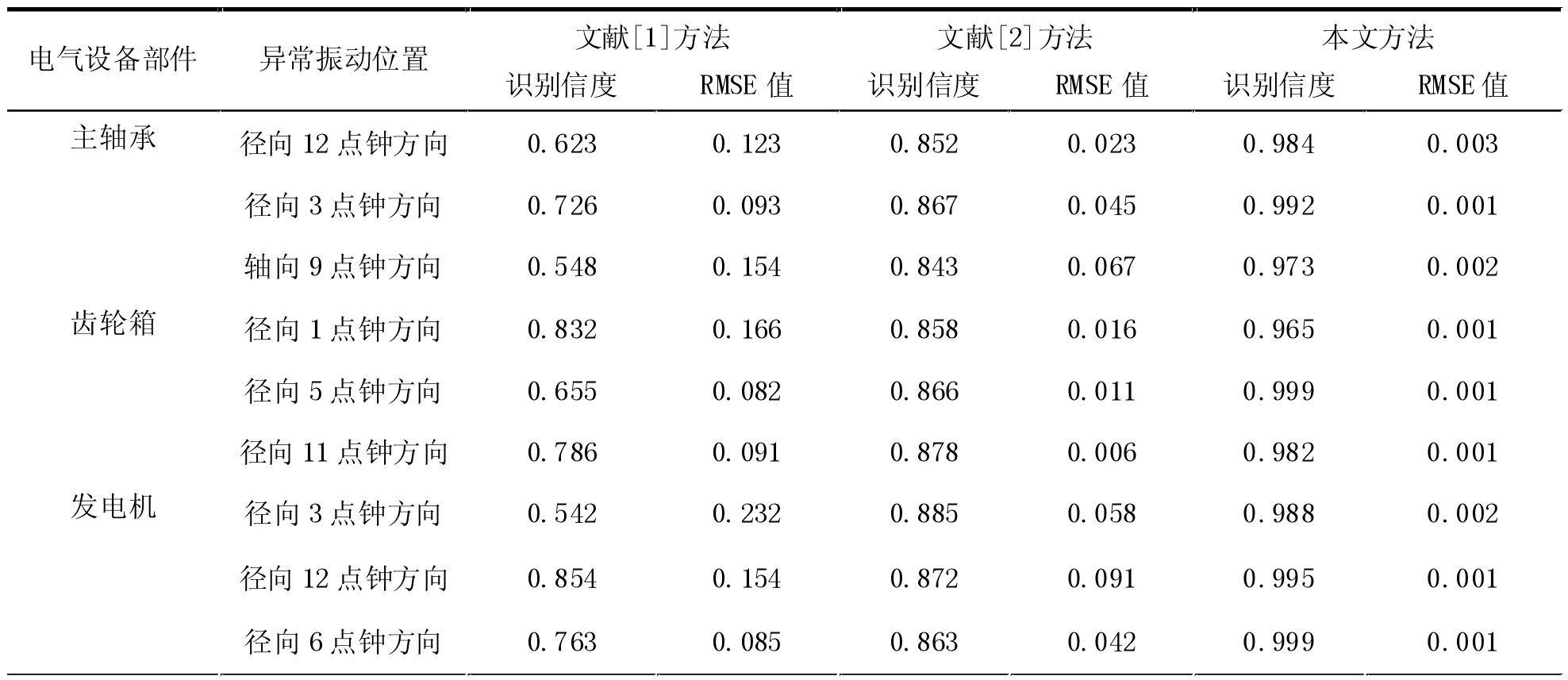
表2 實驗結果

表2 中，在其他條件均一致的情況下，使用文獻[1] 方法之后，識別信度在0.54～0.86 的范圍內變化；RMSE 值在0.08～0.25 的范圍內變化。由此可見，使用該方法之后，異常振動識別的隨機誤差較大，振動數據識別的準確性相對較低，亟需對其進行優化。使用文獻[2]方法之后，識別信度在0.84～0.89 的范圍內變化；RMSE 值在0.01～0.10 的范圍內變化。由此可見，使用該方法之后，識別信度較為穩定，整體數據能夠滿足基本識別需求。但是，該方法的識別誤差仍然存在，影響異常振動識別效果。而使用本文方法之后，識別信度在0.96～1.00 的范圍內變化；RMSE 值在0.001～0.005 的范圍內變化。由此可見，本文方法的異常振動識別有效性較高，隨機誤差較低。

結束語

電氣設備在運行過程中如果發生故障或失效，將會給企業帶來巨大的經濟損失。為此，針對電氣設備的異常振動問題，本文利用隨機森林算法設計了電氣設備異常振動識別方法。從異常諧波特征、識別模型、劣化狀態識別等方面，降低了電氣設備異常振動狀態識別的隨機誤差，為電氣設備的運行與維護提供了保障。