特高壓輸電線路拉線塔拉線- 金具系統的風載荷計算及疲勞特性分析
黃青松,王曉兵,王東陽,孫俊龍
(1.平高集團有限公司,河南 平頂山;2.河南省建設科技和人才發展中心,河南 鄭州)
拉線塔具有柱身斷面小、施工周期短、穩定性好等一系列優勢,在高壓和特高壓輸電線路中被廣泛應用。隨著拉線塔使用年限的增加,由于材料自身老化以及多次重復荷載作用的影響,材料的屈服極限降低,容易出現疲勞破壞,嚴重時還有可能導致拉線塔的倒塌。其中,拉線塔上的拉線- 金具系統由于受力特殊,是疲勞分析的重點對象。分析拉線- 金具系統的疲勞特性,能夠為今后特高壓輸電線路拉線塔的結構優化與日常維護提供參考,對保障特高壓輸電線路安全有一定幫助。
1 拉線- 金具系統的風載荷計算
位于野外空曠地帶的拉線塔,在風力作用下會產生風振疲勞損傷,并且風速的大小與疲勞損傷的程度密切相關。在三維空間中,各個方向上風的出現頻率和強度均表現出明顯差異;在低風速時,風速方向的分布較為離散。為了更加準確地描述風載荷對拉線-金具系統的影響,本文運用概率密度函數描述風的特征,該函數可表示為:
式中,P、Q 為描述任意方向上不同大小風速出現概率的可變參數,v 表示平均風速。各個方向上的P 值、Q值以及出現風的百分比如表1 所示。
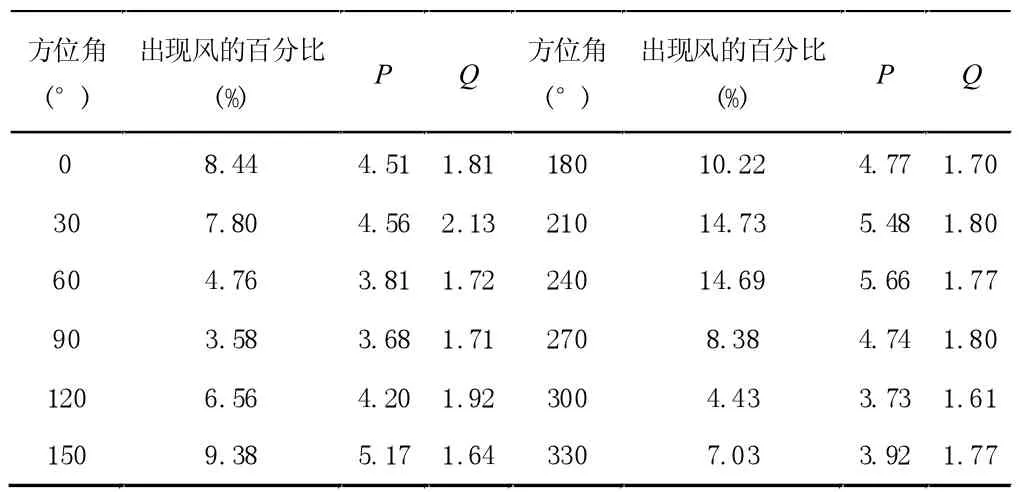
表1 風在各個方向上的出現頻率
將表1 中的P 值、Q 值代入到式(1)中,可以求得任意方向上風速的分布概率。這里以240°方向為例,各個風速的分布概率如圖1 所示。
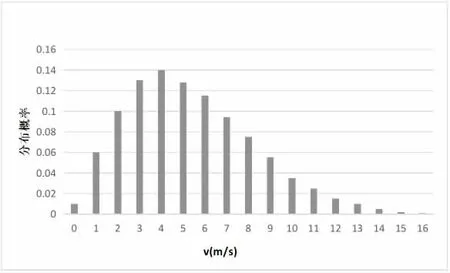
圖1 某地240°方向上各平均風的概率分布
結合圖1 可知,該地區240°方向上,分布概率最高的風速為4 m/s;其中,10 m/s 以上的高風速分布概率僅為0.093,占比不足10%,說明該地區大風出現概率較低。
2 疲勞破壞區應力幅統計
2.1 單柱拉線塔的模型構建
結合以往的拉線塔維修經驗以及查閱相關資料,可以得出“拉線- 金具系統疲勞斷裂主要分布在應力集中區”的結論。在特高壓輸電線路的拉線- 金具系統中,金具通過液壓壓接的方式將拉線與拉線塔連接起來。為了保證兩者連接牢固,需要在壓接管口位置施加一個較大的作用力,由此產生了應力集中現象。在拉線- 金具系統的疲勞特性分析中,將金具與拉線接觸的壓接管口位置作為疲勞破壞區進行重點分析[1]。
本文參照某地800KV 直流輸電線路中的單柱拉線塔,使用ANSYS 軟件構建了拉線塔仿真模型,導線型號為JL/G3A-1000/45,截面積1 036 mm2;地線型號為LBGJ-150-20AC,截面積為150 m2,參數設置如表2 所示。

表2 單柱拉線塔工程條件
仿真模型搭建完成后,在拉線塔上施加一個初始預應力,隨后改變風載荷條件,模擬拉線塔在不同風向、不同風速下的風振響應,并繪制10 min 內拉線軸向應力時程曲線。從該曲線中,提取出疲勞破壞區的應力時程曲線,利用“雨流計數法”求出拉線- 金具系統疲勞區的應力幅。
2.2 拉線- 金具疲勞區應力幅的統計方法
目前計算拉線- 金具系統的累計疲勞損失,常用的做法是將應力幅的幅值進行細分,分別計算出每個部分應力幅值的出現次數,最后求和。在幅值統計過程中,需要運用到循環計數法、雨流計數法等方法。本文選用“雨流計數法”,其原理是將“應力- 時間歷程”數據記錄旋轉90°,使時間坐標軸垂直線下,讓應力值像雨水一樣自上而下流動。具體實現過程為:
步驟1:將“應力- 時間歷程”曲線以順時針方向轉動90°,規定垂直向下的軸線為時間軸,水平向右的軸線為應力軸。
步驟2:任意選定一個峰值或谷值開始計數。假設從峰值開始計數,如果一個從峰值開始的流動到達臨近谷值時,判斷下一個峰值與開始峰值的大小。如果下一個峰值較大,則流動停止;反之,如果下一個峰值較小,則繼續流動。
步驟3:流動結束后,流動軌跡在應力軸上的投影長度,即為該半循環的幅值[2]。
使用雨流計數法,統計10 min 內沿120°方向平均風速為10 m/s 時,各應力水平結構實際循環次數百分比,結果表明:應力幅為1 MPa 的循環次數百分比最高,達到了44.7%;隨著應力幅的增加,循環次數百分比逐步下降,在應力幅超過10 MPa 后,循環次數百分比降低至1%以下。
2.3 拉線- 金具疲勞區應力幅的計算結果
現有的研究表明,在應力循環方式不同的情況下,只要保證應力幅一致,那么應力對構件及其連接件的疲勞效應是相同的。由此可見,要想延長拉線-金具系統的疲勞壽命,必須要將應力幅作為重點研究對象。參考《鋼結構設計規范》(GB50017-2017)中的有關規定,對于焊接結構,若應力幅為常量時,可采取下式進行疲勞計算:
式中,Δρ 表示應力幅。對于焊接結構,取應力循環中最大拉應力與最小拉應力之差;[Δρ] 表示常幅疲勞的容許應力幅,可通過下式求得:
式(3)中,n 表示應力循環次數;k 和λ 為系數,由拉線- 金具系統中構件和連接類別決定,具體取值見表3。
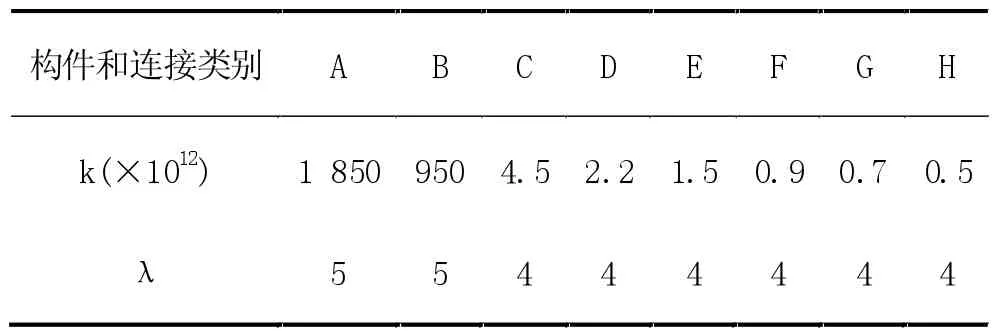
表3 系數k 和λ 的取值表
參考《鋼結構設計規范》(GB50017-2017)中的有關規定構件和連接類別總計8 種,以字母A~H 表示[3]。經過對比,本文研究的拉線- 金具系統與第7 種構件和連接類別(即表3 中G 欄)最為接近,因此在計算中k 值為0.7×1012,λ 值為4。將數據帶入式(3)后可以求得常應力幅下的“應力幅- 循環次數(S-N)”曲線,如圖2 所示。
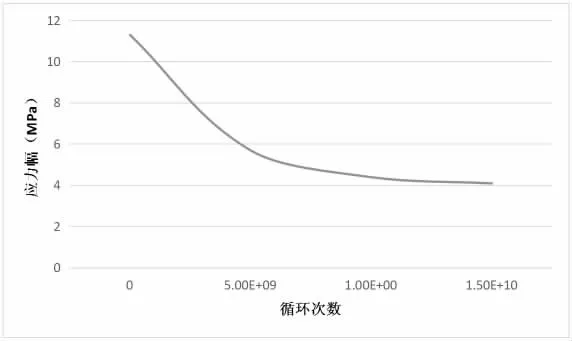
圖2 材料S-N 曲線
上文討論了應力幅為常量情況下拉線- 金具系統的疲勞計算方法。而實際中,由于材料自身特性、外界風力變化等多種因素的影響,應力幅通常為變量(變幅疲勞)。對于變幅疲勞情況,可采用線性累積損傷公式求解拉線- 金具系統的疲勞,計算公式為:
式(4)中,Δi表示應力幅為Δρi破壞時對應的循環次數為ni時的累積損傷;Ni表示應力幅為Δρi,并且出現疲勞破壞時對應的循環次數,即疲勞壽命。將式(3)代入到式(4)中,可以得到:
當Δ 為1 時,結構發生疲勞破壞。
3 拉線- 金具結構的疲勞壽命預測
由于風載荷的隨機性,拉線塔結構的響應也表現出隨機特點。為了準確估算出變幅應力下拉線塔拉線- 金具結構的疲勞壽命,可使用Miner 線性累積疲勞損傷理論進行計算[4]。公式為:
式(6)中,任意選擇3 組點(假設為n1N1、n2N2、n3N3),以N 為橫坐標,以n 為縱坐標,在平面坐標系上標記出3個點的位置,然后用直線將3 個點連接起來,即可得到“S-N”曲線,如圖3 所示。
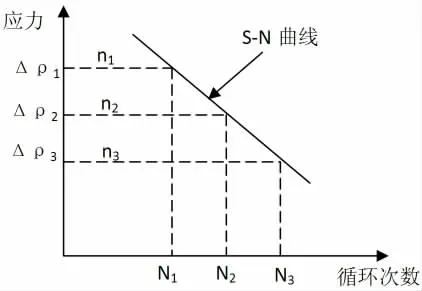
圖3 Miner 理論示意圖
由圖3 可知,在該坐標系中,任意一個應力水平Δρi,對應的破壞循環次數為Ni,則Ni的表達式為:
式中,ΔρF表示變幅疲勞極限應力幅,NF表示對應ΔρF的循環次數,λ 表示傾斜度。為了便于分析,本文通過一個等效的應力水平與破壞循環次數,代替原來多種應力水平下的實際循環次數[5]。則等效破壞循環次數(Ne)可表示為:

計算后式(9)左側為9.03×1010,Sum 為0.14。令Ne取107,將各項數據帶入式(9)后,求得Δρe的值為40.12 N/mm2。在此基礎上,利用上文給出的式(3),計算構件疲勞破壞循環次數。將式(3)兩邊進行對數處理,計算公式變為:
求得lgn=7,相應的n=107,即構件疲勞循環次數(疲勞壽命)為107次。
在估算出拉線塔拉線- 金具系統的使用壽命后,能夠為后續的檢修維護工作提供參考。工作人員可以在拉線- 金具系統即將達到疲勞壽命時,對其進行更換,從而保證了拉線塔拉線- 金具系統的可靠運行,對保證特高壓輸電線路的運行安全起到了積極幫助。
4 結論
在特高壓輸電線路中,相比于常見的自立塔,拉線塔表現出結構簡單、安裝方便、受力性能好等優勢,尤其是在地形復雜的山區有著廣泛使用。拉線塔的拉線- 金具系統在長期受到風載荷的影響后,容易出現不同程度的疲勞損壞,如果不能及時處理可能會出現拉線斷裂等問題,不僅影響特高壓輸電線路的正常供電,而且還會帶來嚴重的安全隱患。采用雨流計數法求得疲勞破壞區應力幅循環次數,在此基礎上基于Miner 線性累積疲勞損傷理論,估算出拉線- 金具系統的疲勞壽命,讓拉線塔拉線- 金具系統的疲勞損傷情況得以量化表示,為檢修維護工作的開展提供了依據,切實保證了拉線塔的結構安全。

