海上風電經VSC-HVDC系統受端電網不對稱故障抑制策略*

陳 立, 王正齊, 葉冰藝, 陸 鵬

(南京工程學院 電力工程學院,江蘇 南京 211100)

0 引 言

近幾年,隨著“新能源電力系統”和“雙碳目標”的提出,海上風電送出技術取得了迅速發展[1-2]。由于柔性直流輸電技術(即基于電壓源換流器的高壓直流輸電系統,VSC-HVDC)可以阻斷風電場與交流系統之間的故障傳播,實現海上風電機組的靈活控制,海上風電機組通常采用VSC-HVDC輸電方式接入受端交流電網。然而這種方式使得受端電網的運行情況變得復雜,尤其是受端電網不對稱故障產生的負序分量易在換流站的交直流側互相傳播[3-4],從而影響整個系統的正常運行。因此,研究海上風電經VSC-HVDC送出系統中受端電網不對稱故障具有重要意義。

海上風電經VSC-HVDC送出系統中受端電網故障與柔性直流輸電系統中受端電網故障具有相通之處,因此可以借鑒。目前,關于柔性直流輸電系統中受端電網不對稱故障的負序分量抑制策略主要分為以下三大類:(1)以雙環控制器為基礎的正負序分離控制策略[5];(2)以抑制二倍頻功率為基礎的功率補償控制策略[6];(3)負序電壓補償控制策略[7]。上述的第一類方法通常以雙環PI控制器為基礎建立正序控制器和負序控制器,簡便實用,但抑制諧波能力較弱。尤其是逆變側交流系統發生不對稱故障時產生的負序分量會使得直流電壓和電流含有二倍頻諧波[8-9],反過來直流側的諧波也會對交流側產生影響。若諧波抑制能力較弱,系統的正常運行將會受到影響。第二類方法可以實時控制換流站交直流側的功率平衡,實現功率傳輸,但這種方法需要采用陷波器對輸出功率進行實時濾波,增加了控制系統的階數。第三類方法可以有效抑制負序電流,實現限流控制,但需要計算電壓的矢量相位,導致控制比較繁瑣。

本文借鑒第一類方法的優點,重點對正負序分離控制器進行深入研究,應用Lyapunov函數控制取代傳統PI控制。Lyapunov函數方法是分析閉環系統關于其平衡點行為的一種非常實用的技術[10-12],因此可以用來確定VSC換流站在其平衡點附近的全局穩定性。如果VSC的總能量連續耗散,狀態變量則收斂到平衡點。其主要目的是通過使Lyapunov函數始終為負來找到一個確保系統全局穩定性的控制規律。綜上所述,可利用Lyapunov函數方法實現故障條件下對目標變量較好地控制。因此,本文首先建立海上風電機組經VSC-HVDC送出系統的拓撲結構,并利用受端VSC換流站拓撲及其數學模型進行不對稱故障分析,指出了由負序分量引起的諧波在受端交直流側的傳播機理;其次,設計了基于Lyapunov函數方法的正負序控制器,并求解相應的控制器系數;最后,基于MATLAB/Simulink仿真軟件將所提方法與傳統PI控制進行對比,突出其諧波抑制的優勢。

1 系統拓撲和受端交流系統不對稱故障分析

1.1 系統拓撲

圖1為海上風電經VSC-HVDC送出的系統拓撲結構圖。由圖1可知,海上永磁直驅風電機組通過機側換流器和網側換流器送出50 Hz的三相交流電,經風電匯集線路和4.16 kV/220 kV升壓變壓器送至并網點。文獻[13-14]對直驅風電機組、機側換流器以及網側換流器展開了詳細介紹,因此本文將不再贅述。并網點處的電能通過220 kV/150 kV降壓變壓器、VSC-HVDC輸電系統以及150 kV/220 kV升壓變壓器輸送至受端電網。其中,送端VSC1換流站采用VF控制策略實

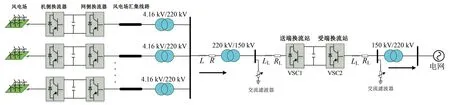
圖1 海上風電經VSC-HVDC送出的系統拓撲結構

現風電并網的電壓和頻率控制,受端VSC2換流站采用定直流電壓控制。

送端交流系統的支撐僅來自于海上風電機組,與其不同的是,受端電網的組成比較復雜,故障特征難以捕捉。海上風電機組又因為遠離受端電網,無法針對受端電網故障對控制系統進行實時調控,則導致整個系統的故障控制效果較差。因此,有必要對受端電網故障進行詳細分析,并提出相應的策略抑制其影響。

1.2 受端交流系統不對稱故障分析

為了深度分析受端VSC側換流站交流系統的不對稱故障特征和傳播機理,圖2給出了VSC側換流站的詳細模型。系統穩態時,圖2所示拓撲的數學模型為[15]

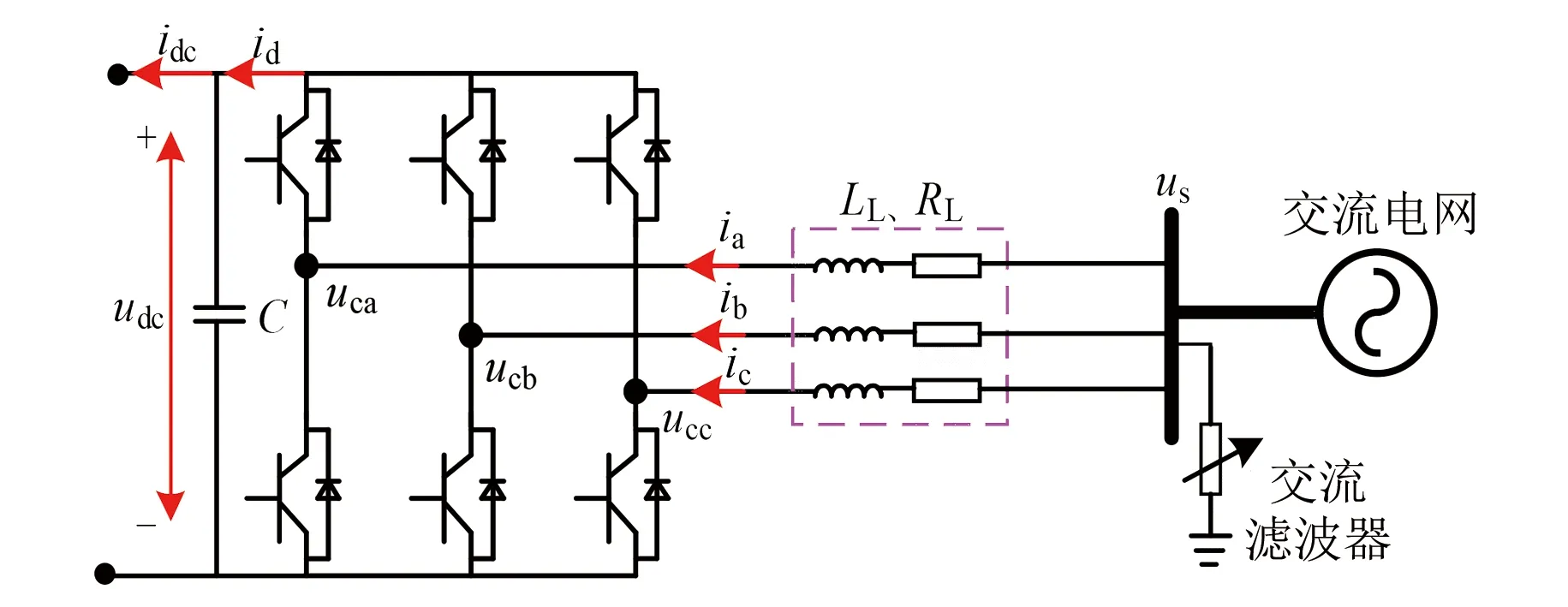
圖2 受端VSC換流站的詳細模型

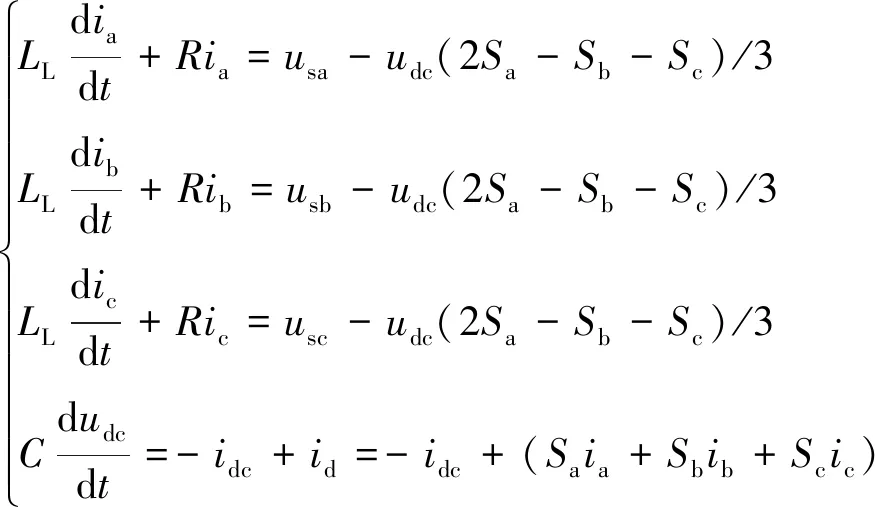
(1)

式中:idc和udc分別為受端換流站的直流電流和直流電壓;id為三相橋臂電流饋入至直流側的成分;ia、ib、ic為交流電網饋入至換流站的三相電流;RL和LL分別為換流站出口線路的電阻和電感;us為換流母線處電壓;uca、ucb、ucc分別為VSC換流站輸出的三相電壓;Sa、Sb、Sc分別為換流站三相橋臂的開關函數。

通常情況下,VSC側換流站與交流系統連接的換流變壓器的接線為YNd型,所以零序電流不會通過VSC換流站,只需要考慮故障電流的正序和負序分量即可[16]。此時,三相短路電流可表示為

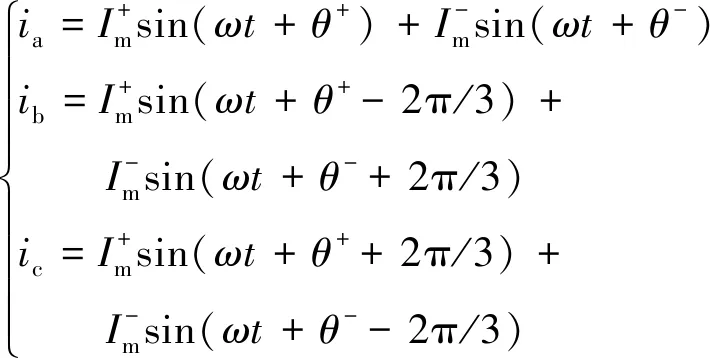
(2)

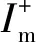
假設VSC換流站交流系統發生短路的瞬間,換流站內三相橋臂的開關函數仍然保持對稱,則存在以下關系:

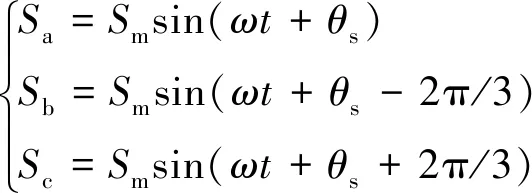
(3)

式中:Sm為三相開關函數的幅值,θs為開關函數的相角。

此時,饋入至直流側電流的分量id為

id=Saia+Sbib+Scic=

Smsin(ωt+θs+2π/3)·

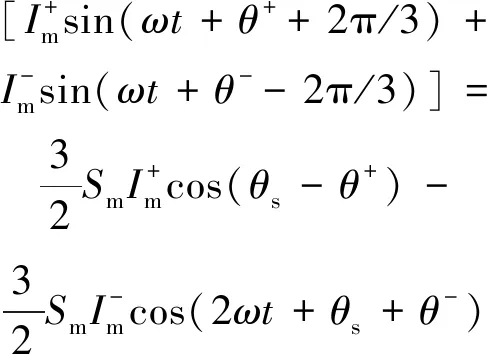
(4)

由式(4)可知,交流系統發生不對稱故障時將會在三相橋臂的直流電流中產生一個二倍頻負序分量,進而引起直流側電壓也含有二倍頻諧波。此時,可定義故障后直流側電壓為

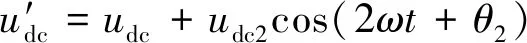
(5)

式中:udc2為二倍頻電壓幅值;θ2為二倍頻電壓的相角。

VSC換流站輸出電壓與直流側電壓存在以下關系,ucx=Sxudc(x=A、B、C)。以A相為例,故障后VSC換流站輸出的A相電壓為

Smsin(ωt+θs)·[udc+udc2cos(2ωt+θ2)]=

Smudcsin(ωt+θs)+

sin(-ωt+θs-θ2)]

(6)

由式(6)可知,直流電壓的二倍頻諧波將在換流站的交流系統中產生一個三倍頻交流電壓諧波。反之,交流系統的三倍頻諧波又會在直流側電壓中產生一個四倍頻的諧波。因此,提出相應的控制策略抑制負序分量顯得尤為重要。

2 基于Lyapunov函數方法的負序分量抑制策略

上一章節主要敘述了系統拓撲和受端交流系統發生不對稱短路故障的特征,尤其是故障后產生的負序分量將會擴大故障的傳播范圍,影響直流系統的安全運行。因此,本章節將提出一種基于Lyapunov函數方法的負序分量控制策略。由式(1)可得到dq軸坐標系下正序分量、負序分量的數學模型,可表示為

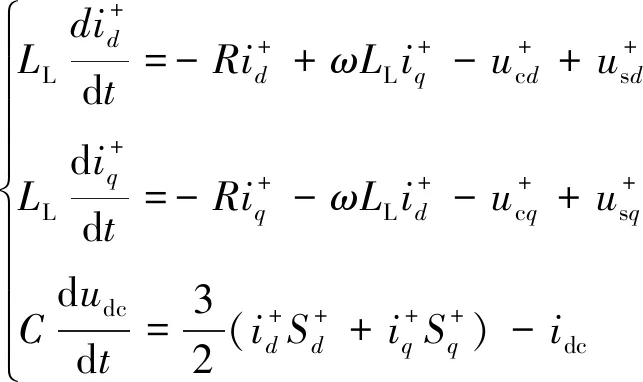
(7)

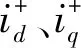
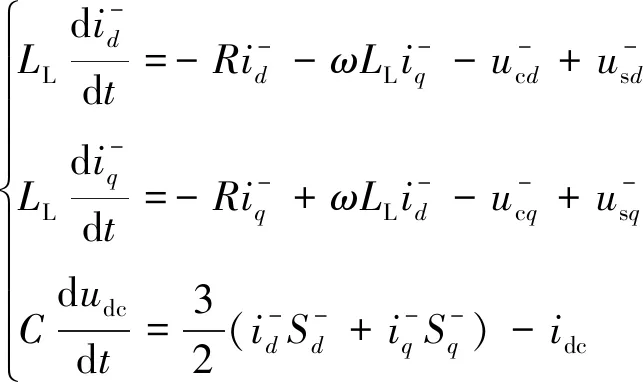
(8)

式中:id-、iq-分別為三相電流ia、ib、ic在dq軸上的負序分量。

以下將以負序分量的數學模型為例介紹Lyapunov函數控制器的設計。定義狀態變量函數為

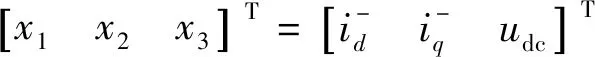
(9)

則狀態變量的參考值為

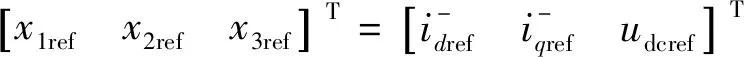
(10)

將式(9)與式(10)作差,可得到狀態變量的誤差函數為

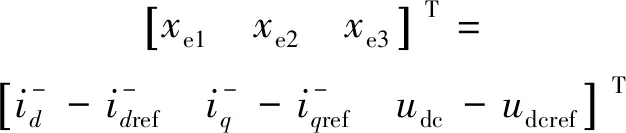
(11)

故參考式(8)可得到負序分量的誤差狀態方程為

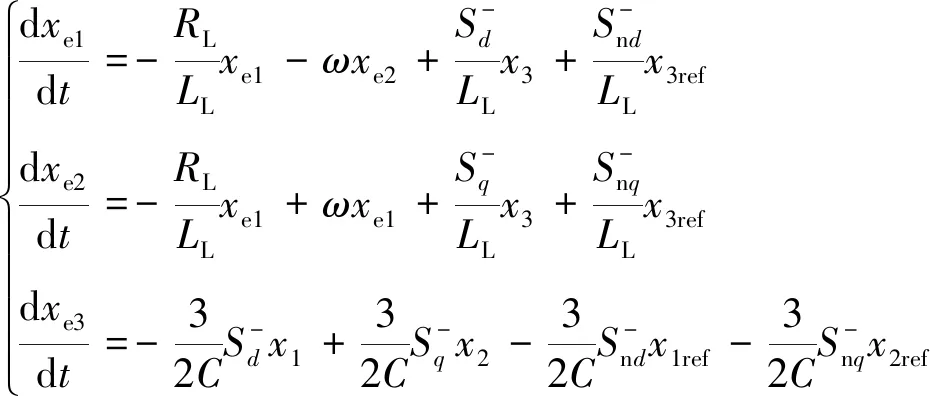
(12)

假設狀態變量在穩態時能夠跟蹤到其參考值,則穩態時負序分量在dq軸上的狀態變量為

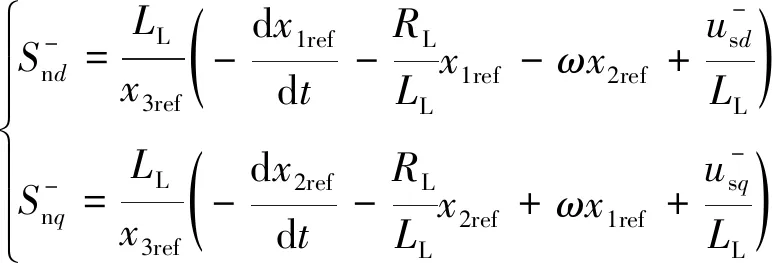
(13)

Lyapunov函數法是分析閉環系統中平衡點運行軌跡的重要方法,其可以用來確定約束條件下系統在平衡點附近的全局穩定性。如果系統的總能量持續耗散,則狀態變量將收斂到平衡點。其主要方式是通過使Lyapunov函數始終為負,找到一個確保系統全局穩定的控制律函數。根據以上分析,如果用V(x)表示的Lyapunov函數,則具有以下特征[18-20]:

(1)V(0)=0;

(2) 對于x≠0時存在V(x)>0;

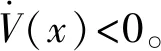
此時,定義誤差控制率函數

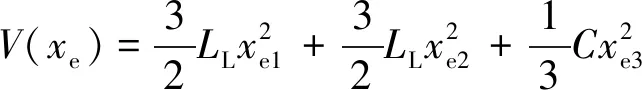
(14)

對式(14)兩邊求導可得如下表達式:

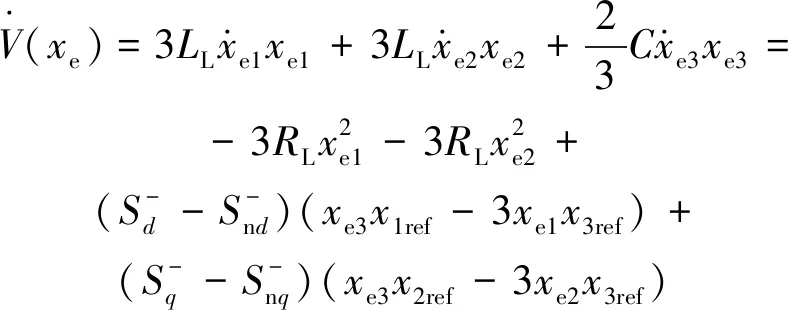
(15)

令

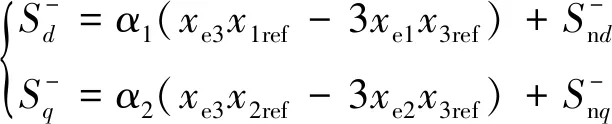
(16)

式中:α1、α2為系數,且假設存在以下關系α1=α2<0,則Lyapunov控制率函數的第三條特征能夠滿足。

結合式(13)和式(16)可得到PWM調制的開關函數,并設計相應的負序控制器為

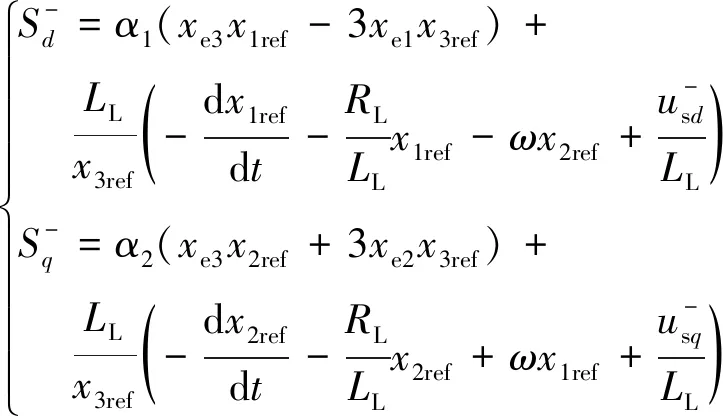
(17)

觀察式(17)可知,如果能夠給出系數α1、α2的取值,則負序控制器將被較好的設計。假設狀態變量在t時刻的參考值為X1ref、X2ref、X3ref,令

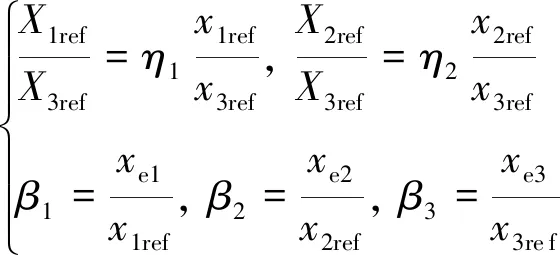
(18)

式中:η1、η2為參數變量因子,且滿足η1>0、η2>0。

將式(18)代入式(15)中,并結合式(16)可得:

(β3-3β1)+3RLβ12]-

(β3-3β2)+3RLβ22]

(19)

定義以下兩個函數為

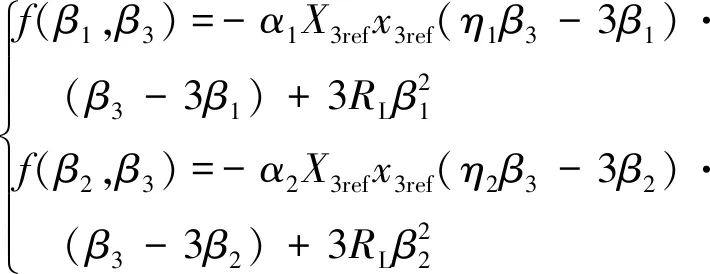
(20)

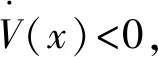
以下以f(β1,β3)函數為例來分析α1的取值,令

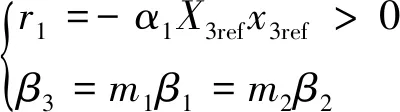
(21)

式中:m1和m2為相關系數。

將式(21)代入式(20)可得:

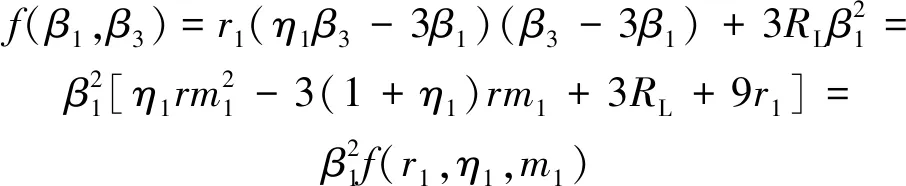
(22)

式(22)中函數f(r,η1,m1)是以變量m1為未知數的一元二次方程,且其開口方向向上,故該方程存在最小值:

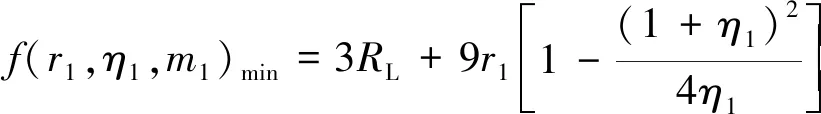
(23)

如果f(r1,η1,m1)min>0,則f(β1,β3)>0。當f(r1,η1,m1)min>0時,存在以下關系:

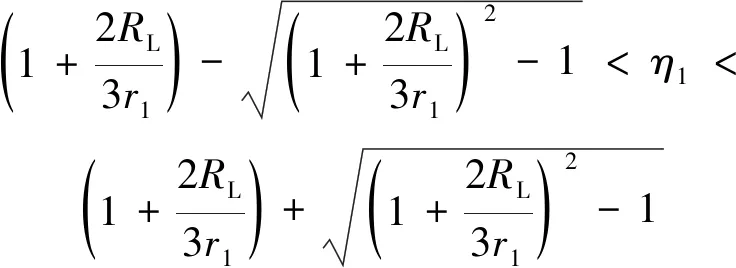
(24)

若存在小于1的正數系數ε1,滿足以下關系η1∈ (1-ε1,1+ε1),則有

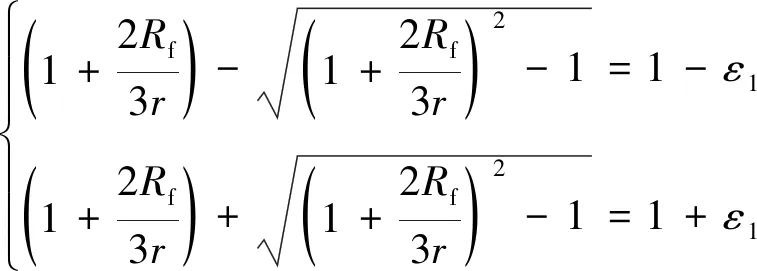
(25)

利用式(23)和式(24)可求得α1的取值范圍為

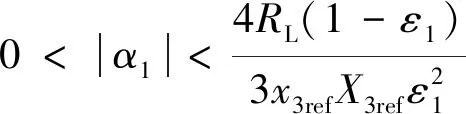
(26)

綜上,將求解出的α1代入式(17)即可進行負序控制器的設計。同理,可參照上述過程設計相應的正序控制器。根據上述控制器的設計過程可以得到圖3所示的基于Lyapunov函數策略的正、負序控制器的結構框圖。

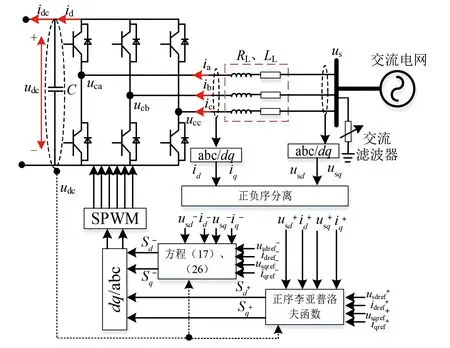
圖3 受端VSC換流站控制系統結構框圖

3 仿真分析

為了驗證所提控制策略的正確性和優越性,仿真在MATLAB/Simulink軟件中搭建了圖1所示的風電機組經VSC-HVDC送出系統的拓撲結構。其中,永磁同步發電機(PMSG)風機采用定功率模式,單臺風機的參考有功功率設定為5 MW,共有60臺風機,輸送300 MW功率。以下以單臺風機的參數為例介紹仿真參數:空氣密度設定為1.225 kg/m3,最大風能利用系數為0.48,風機直徑為119.85 m,最佳葉尖速比為8.1,風速設定為11.46 m/s;機側換流器采用定有功功率控制,功率外環PI控制器的參數為kp=0.000 1、ki=0.02,內環電流環的PI控制器參數為kp=20、ki=200;網側換流器采用定直流電壓和定無功功率控制,直流電壓設定為8 kV,參考無功功率設定為0 var,外環定直流電壓控制的PI控制器參數設定為kp=5、ki=100,外環定無功功率控制的PI控制器參數設定為kp=0.000 02、ki=0.002,內環均采用PI控制,參數設定為kp=50、ki=100;柔直送端環流站VSC1外環采用VF控制,控制器參數設定為kp=0.5、ki=50,內環PI控制器參數為kp=0.5、ki=50;柔直受端換流站VSC2采用定直流電壓控制,直流電壓設定為300 kV,外環PI控制器參數為kp=5、ki=100,內環電流環采用本文所提的Lyapunov函數方法,系數α1、α2設定為-0.001;柔直直流側電容C設定為0.002 F,受端交流系統阻抗參數為RL=75×10-3Ω、LL=25×10-3Ω。以下將從穩態運行驗證所提策略的正確性,從不對稱故障對比驗證所提策略的優越性。

3.1 穩態運行

為了驗證所提策略的正確性,圖4給出了系統穩態運行時的仿真波形。其中,圖4(a)和(b)為VSC-HVDC系統直流電壓和直流電流波形,圖4(c)和(d)為風電機組輸出功率和VSC-HVDC系統輸出功率波形圖。由圖4可知,直流電壓數值約為300 kV,與理論需求一致。風電機組輸出有功功率約為300 MW,與VSC-HVDC輸送直流功率的數值基本一致。此外,由功率計算式可知,直流電流理論數值為1 kA,與仿真數值基本一致。以上仿真結果驗證了所提策略的正確性。

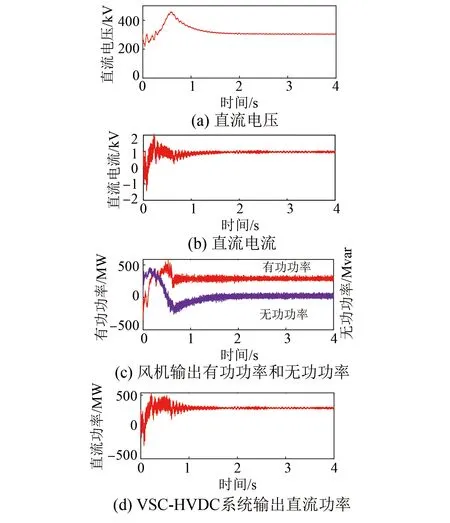
圖4 穩態仿真波形

圖5是2 s時風機風速發生變化時的仿真波形。其中,圖5(a)、(b)、(c)分別是是風機風速、直流電壓以及直流電流波形圖,圖5(d)、(e)分別是風電機組輸出功率和VSC-HVDC系統輸送直流功率波形圖。由圖5可知,仿真中設定2 s時風機風速驟然降低,VSC-HVDC系統的直流電壓出現短時波動后恢復至300 kV,直流電流由于風電機組輸出功率下降從而呈現遞減趨勢。另外,觀察圖5(b)可知,風電機組輸出功率發生變化時VSC-HVDC系統能夠及時參與調整,驗證了仿真模型的正確性。

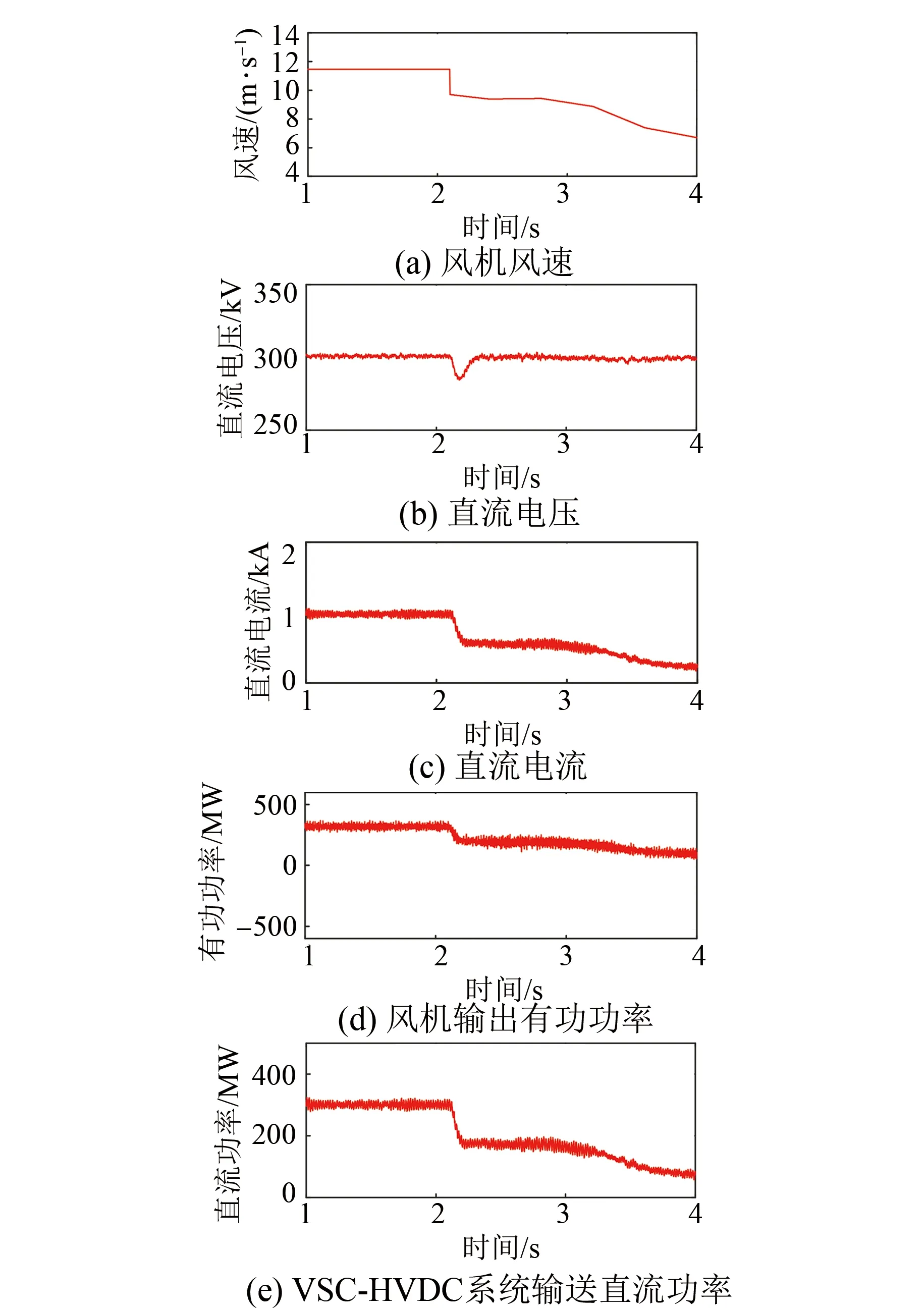
圖5 2 s時風機風速變化時仿真波形

3.2 不對稱故障運行

為了驗證所提策略在諧波抑制方面的優勢,仿真將Lyapunov函數方法與傳統PI控制策略進行對比。圖6和圖7分別給出了兩種策略在單相接地故障情況下受端A相電流、直流電流以及直流電壓諧波。仿真中設定2～3 s時受端交流系統發生單相接地故障,以2 s為初始條件,20個周期進行FFT分析。圖6為Lyapunov函數策略仿真結果,由圖6可知,單相接地故障條件下受端交流系統A相電流諧波為128.18%,直流電流諧波為23.64%,直流電壓諧波為66.85%。然而,PI控制策略下受端交流系統A相電流諧波為267.59%,直流電流諧波為38.63%,直流電壓諧波為115.73%。比較上述兩種策略的仿真結果可知,所提Lyapunov函數策略可以有效抑制單相接地故障情況下電氣量的諧波。

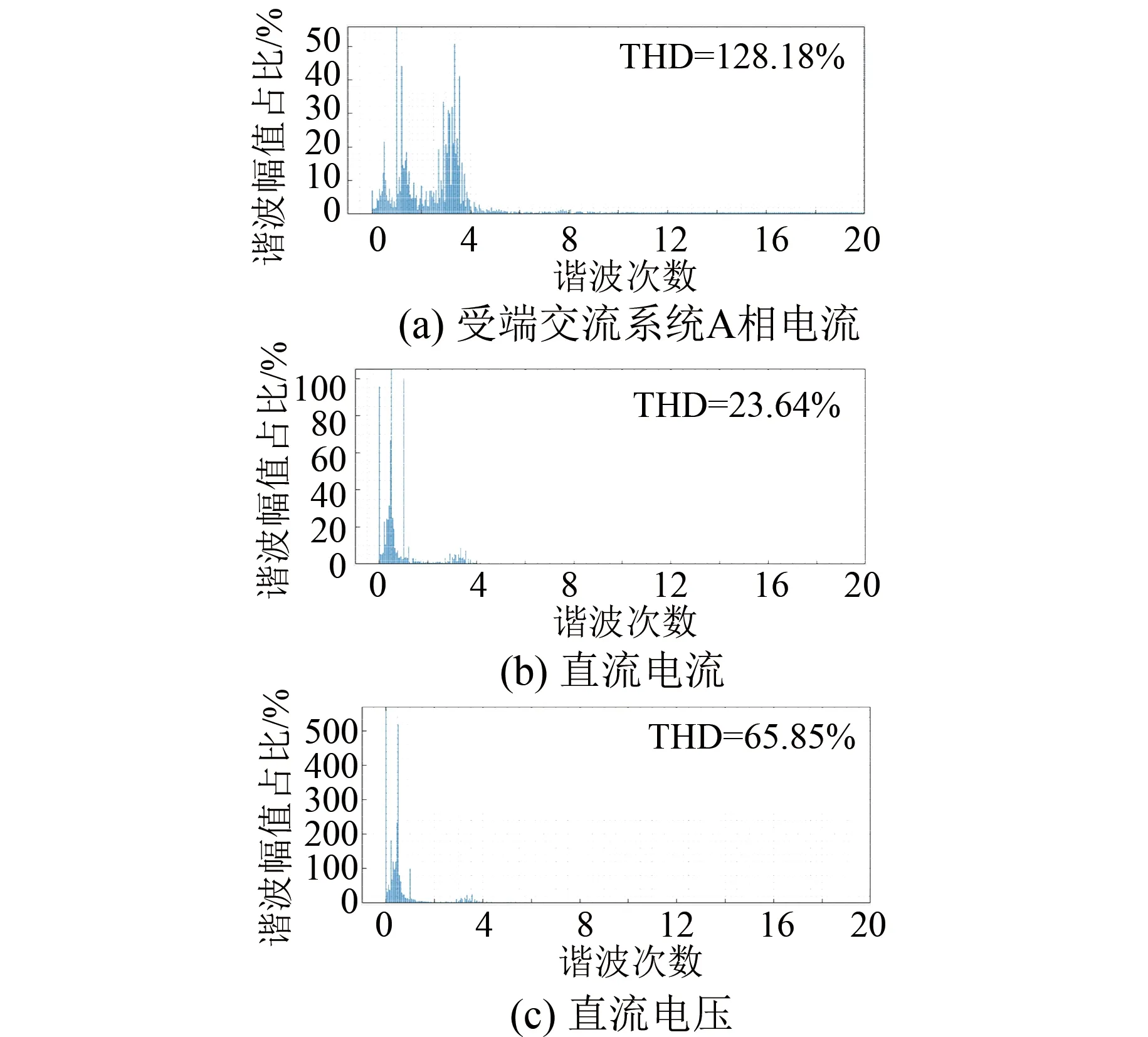
圖6 單相接地故障情況下Lyapunov函數策略輸出波形諧波

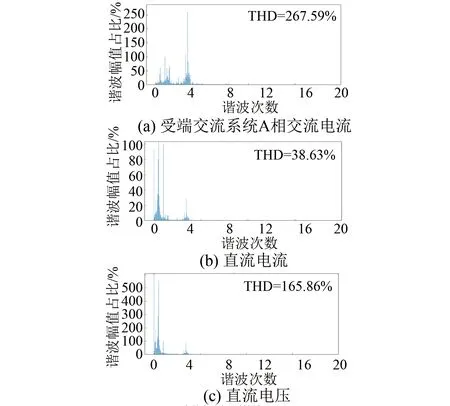
圖7 單相接地故障情況下PI控制策略輸出諧波

圖8和圖9分別給出了兩種策略在兩相接地故障條件下的仿真波形。其中,圖8為Lyapunov函數策略的仿真波形,圖9為傳統PI控制策略的仿真波形。由圖8可知,兩相接地故障條件下受端交流系統A相電流諧波為20.47%,直流電流諧波為33.12%,直流電壓諧波為153.85%。然而,圖9中受端交流系統A相電流諧波為23.94%,直流電流諧波為46.30%,直流電壓諧波為165.86%。以上仿真結果Lyapunov函數策略可以有效抑制兩相接地故障條件下電氣量的諧波。

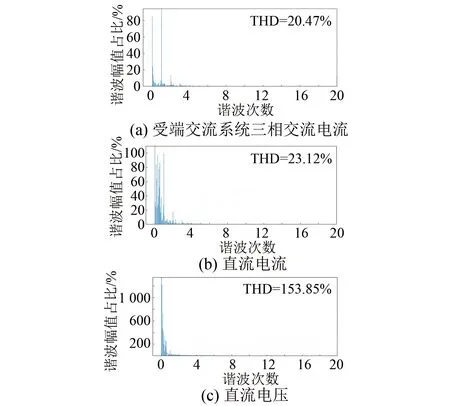
圖8 兩相接地故障情況下Lyapunov函數策略輸出諧波

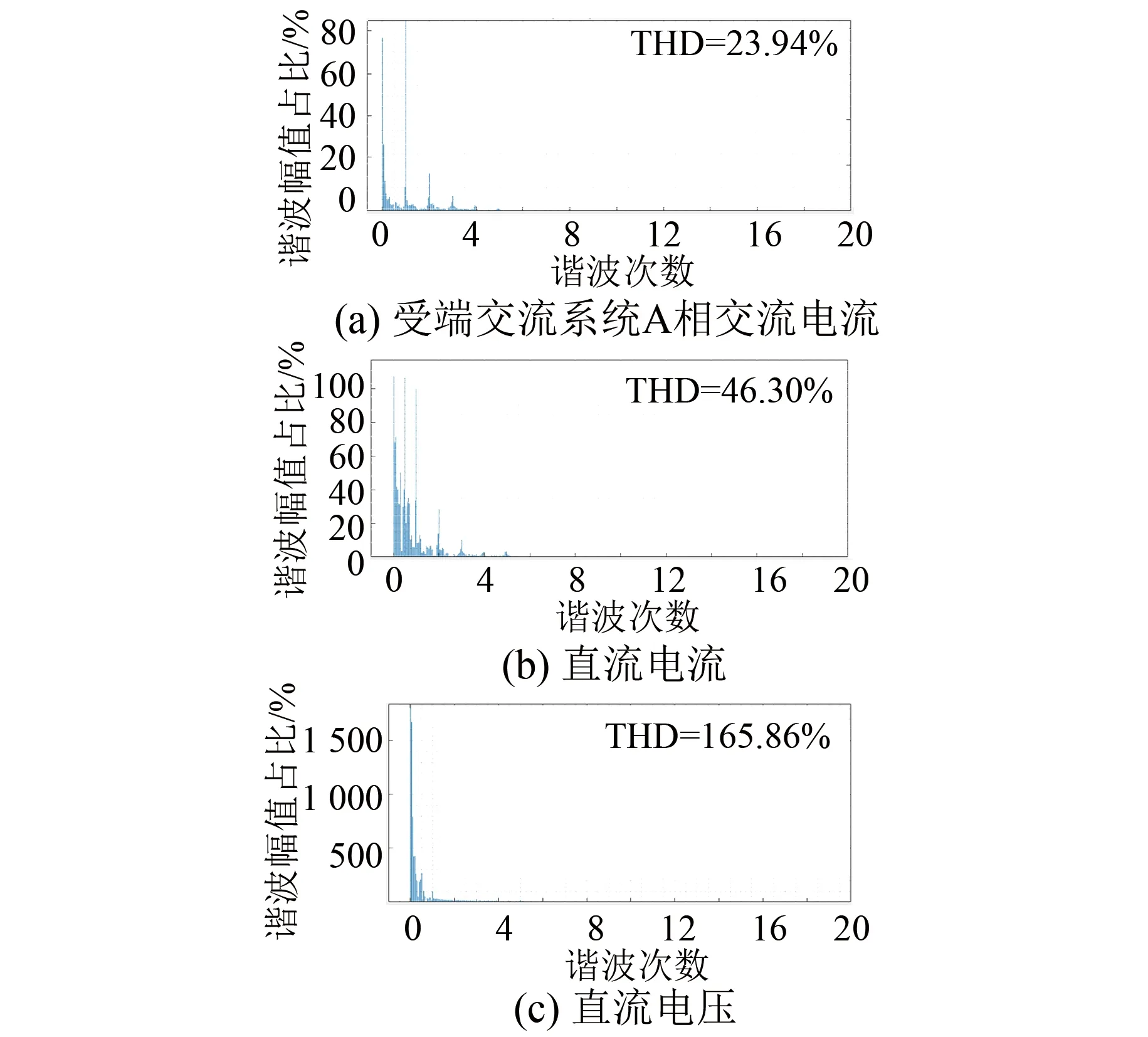
圖9 兩相接地故障情況下PI控制策略輸出諧波

為了更加直觀地突出Lyapunov函數策略在諧波抑制方面的優勢,表1給出了上述兩種案例的仿真結果對比。由表1可知,所提策略抑制不對稱故障條件下電氣量的諧波效果較傳統PI策略好。

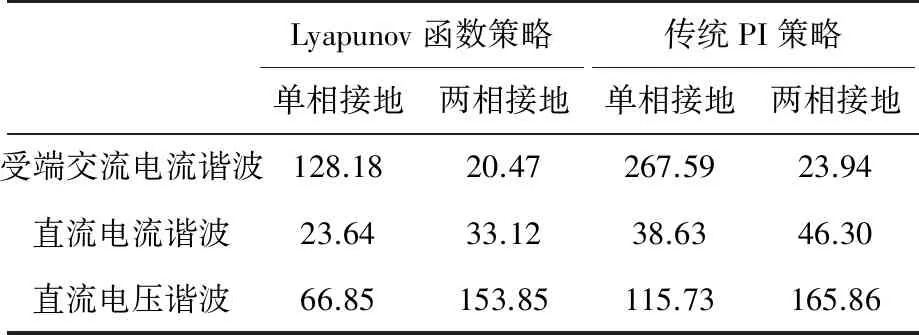
表1 兩種策略的仿真對比 %

4 結 語

本文著重探究了海上風電經VSC-HVDC送出系統中受端電網的不對稱故障分析,并提出了一種基于Lyapunov函數策略的負序分量抑制策略,仿真驗證了所提策略在諧波抑制方面的優勢,可得出以下主要結論:

(1) 受端交流系統發生不對稱故障會在交流側產生奇數次諧波,在直流側產生偶數次諧波;

(2) 所提Lyapunov函數策略較傳統PI策略抑制電壓和電流的諧波效果好,尤其是單相接地故障條件下Lyapunov策略輸出電壓和電流的諧波約為傳統PI策略的1/2。