與二次函數有關的“恒成立”問題的求解策略

■張亮昌

解決不等式恒成立問題常見的方法有:判別式法,分離參數法,主參換位法等。下面舉例分析這類問題的求解策略。

方法一：判別式法

例1已知不等式(m2+4m-5)x2+4(1-m)x+3＞0 對任意實數x恒成立,則實數m的取值范圍是____。

①當m2+4m-5=0時,可得m=-5或m=1。

若m=-5,則不等式化為24x+3＞0,這時對任意實數x不可能恒大于0。若m=1,則3＞0恒成立。

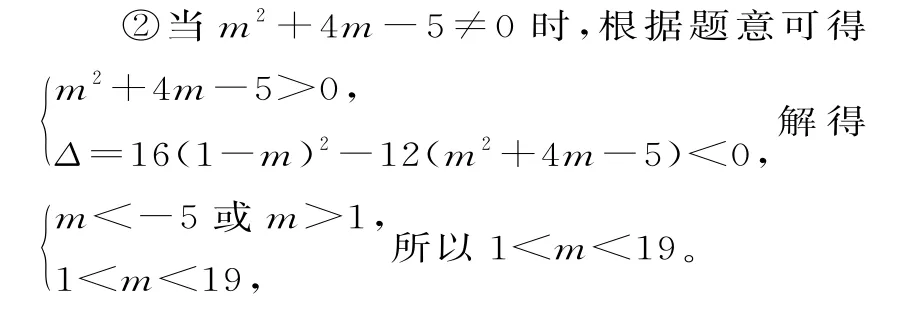
綜上可知,所求實數m的取值范圍是{m|1≤m＜19}。

評注：對于一元二次不等式ax2+bx+c＞0(a＞0)在R 上恒成立,則Δ=b2-4ac＜0;一元二次不等式ax2+bx+c＜0(a＜0)在R 上恒成立,則Δ=b2-4ac＜0。

方法二：分離參數法

例2不等式xy≤ax2+2y2對于1≤x≤2,2≤y≤3恒成立,則實數a的取值范圍是_____。

不等式xy≤ax2+2y2對于1≤x≤2,2≤y≤3恒成立,等價于對于1≤x≤2,2≤y≤3恒成立。

令t=y

x,則1≤t≤3,所以a≥t-2t2在1≤t≤3上恒成立。

故實數a的取值范圍是{a|a≥-1}。

評 注：若a≥f(x)恒 成 立,則a≥f(x)max;若a≤f(x)恒成立,則a≤f(x)min。

方法三：主參換位法

例3已知函數y=ax2-2ax+8+3a,若對于1≤a≤3,y＜0 恒成立,則實數x的取值范圍為____。

已知函數可化為關于a的函數y=ax2-2ax+8+3a=(x2-2x+3)a+8。

由題意知,y＜0對于1≤a≤3恒成立。

評注：在一個函數式中,有兩個自變量,其中給出一個自變量的范圍,這時可把問題轉化為關于已知范圍的那個自變量的函數(本題是一次函數)。

在R 上定義運算?:A?B=A(1-B),若不等式(x-a)?(x+a)＜4對x∈R 恒成立,則實數a的取值范圍為_____。

提示:(x-a)?(x+a)=(x-a)[1-(x+a)]=-x2+x+a2-a＜4對x∈R 恒成立,即x2-x-a2+a+4＞0對x∈R 恒成立,所以Δ=4-4(-a2+a+1)=4a2-4a＜0,所以0＜a＜1,即實數a∈(0,1)。