一元二次函數、方程和不等式常見典型考題賞析

■歐陽亮

一元二次函數、方程和不等式是高中數學的重要內容,也是高考的重要考點。下面就一元二次函數、方程和不等式問題的常見典型考題舉例分析,供大家學習。

題型一：利用不等式的性質判斷不等式的真假

此類問題一般結合不等式的性質,利用作差法或作商法求解,也可以利用特殊值法求解。

例1若a＞b＞0,m＜0,則下列不等式成立的是( )。

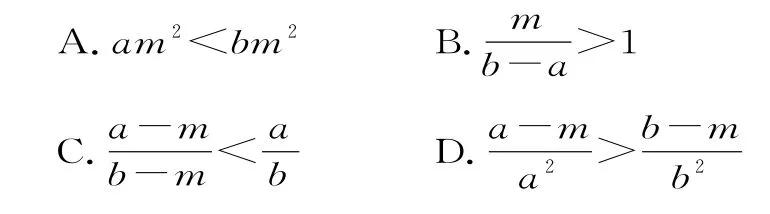
跟蹤訓練1：下列命題正確的是( )。A.若a＞b,c＞d,則ac＞bd

B.若ac＞bc,則a＜b

C.若a＞b,c＞d,則a-c＞b-dD.若,則a＜b

提示：A 中,若a＞b＞0,c＞d＞0,則ac＞bd成立,否則,如2＞1,-1＞-2,可得-2＞-2,顯然錯誤,A 不正確。B 中,若ac＞bc,c＜0,則a＜b,否則,如a=-2,b=-3,c=2,則(-2)×2＞(-3)×2,可得-2＞-3,即a＞b,B 不正確。C 中,如3＞2,2＞1,可得3-2＞2-1,即1＞1,顯然錯誤,C不正確。D 中,由,可知c≠0,則c2＞0,由不等式的性質知不等式兩邊同乘一個正數c2,不等式不變號,即a＜b,D 正確。應選D。

題型二：利用不等式的性質證明不等式

利用不等式的性質證明不等式,其實質就是利用性質對不等式進行變形,變形要等價,要善于尋找欲證不等式的等價條件,利用不等式的性質時要注意性質適用的前提條件。

例2(1)已知a＜b＜0,求證

(2)已知a＞b,, 求證:ab＞0。

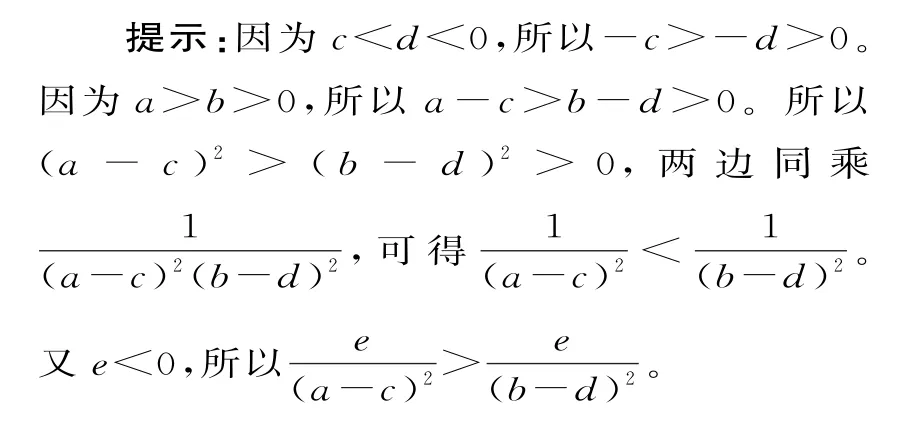
題型三：利用不等式的性質求代數式的取值范圍

根據不等式的性質求代數式的取值范圍,首先要明確同向不等式具有可加性及正的同向不等式具有可乘性,但要注意不等式不能相減,如求a-b的范圍,只能先求-b的范圍,再與a的范圍相加。同理,不等式也不能相除,如求的范圍,只能先求的范圍,再與a的范圍相乘。當不等式兩邊同乘一個數時,要明確所乘數的正負。

例3設2＜a＜3,-4＜b＜-3,求a+b,a-b,,ab的取值范圍。

跟蹤訓練3：已知30＜x＜42,16＜y＜24,求x+y,x-3y的取值范圍。

提示：因為30＜x＜42,16＜y＜24,所以30+16＜x+y＜42+24,即46＜x+y＜66。

因為16＜y＜24,所以48＜3y＜72,所以-72＜-3y＜-48,所以-42＜x-3y＜-6。

題型四：基本不等式的直接運用

在理解基本不等式時,要從形式到內涵中理解,特別要關注條件。運用基本不等式比較大小時應注意成立的條件,如a+b≥成立的條件是a＞0,b＞0,等號成立的條件是a=b;a2+b2≥2ab成立的條件是a,b∈R,等號成立的條件是a=b。

例4(1)若0＜a＜,則a(1-2a)的最大值是( )。

(2)已知x＞-1,則函數的最小值是( )。

A.4 B.3

C.2 D.1

跟蹤訓練4：若a＞1,則的最小值是( )。

A.1 B.2

C.3 D.4

提示：由a＞1,可得a-1＞0,所以a+,當且僅當a=2時取“=”。應選C。

題型五：條件不等式的證明

條件不等式的證明,要將待證不等式與已知條件結合起來綜合考慮,這是不等式證明的一種常見題型。

例5已知a,b,c是互不相等的正數,且a+b+c=1,求證:

證明：由a,b,c∈R+,且a+b+c=1,可

題型六：利用不等式求函數的最值

求函數的最值的常用方法是不等式法,解題時,要注意不等式取等號時的情況。

例6已知函數(x＞0),則f(x)的最小值是_____。

題型七：不等式恒成立中的含參數問題

a≤f(x)恒成立?a≤f(x)的最小值,a≥f(x)恒成立?a≥f(x)的最大值。

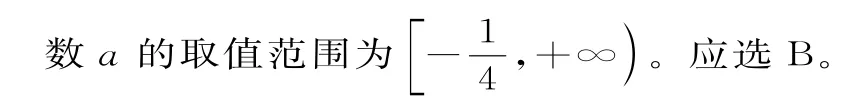
題型八：解含參數的一元二次不等式

解含參數的一元二次不等式的常用方法是因式分解法,解題時,要注意對二次項系數(參數)進行討論。

例8解關于x的不等式:ax2-(a2+2)x+2a＞0(a∈R)。

由ax2-(a2+2)x+2a＞0,可得(ax-2)(x-a)＞0。

已知a∈R,結合a的取值情況,進行分類討論求解集。

當a=0時,則-2x＞0,所以x＜0,可得不等式的解集為{x|x＜0};

當a=-時,可得不等式的解集為?。

跟蹤訓練8：求關于x的一元二次不等式x2-x-a(a+1)＞0的解集。

提示：因為x2-x-a(a+1)＞0,所以(x+a)[x-(a+1)]＞0。令(x+a)[xa+1]=0,所以兩根為x1=-a,x2=a+1。

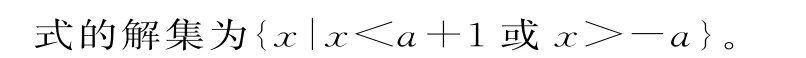
題型九：三個“二次”的關聯問題

一元二次不等式ax2+bx+c＞0(a≠0)的解集的端點值是一元二次方程ax2+bx+c=0的根,也是函數y=ax2+bx+c與x軸交點的橫坐標。二次函數y=ax2+bx+c的圖像在x軸上方的部分,是由不等式ax2+bx+c＞0 的x值構成的;圖像在x軸下方的部分,是由不等式ax2+bx+c＜0 的x值構成的,三者之間相互依存、相互轉化。

例9已 知 方 程x2+（m-2）x+5-m=0的兩根都大于2,則實數m的取值范圍是( )。

A.（- 5,-4]∪[4 ,+∞）

B.（-5,-4]

C.（-5,+∞）

D.[- 4,-2）∪[4 ,+∞）

因為方程x2+(m-2)x+5-m=0的兩根都大于2,所以二次函數y=x2+(m-2)x+5-m的圖像與x軸的兩個交點都在x=2的右側(圖略)。根據圖像可知,方程的判別式Δ≥0;當x=2時,函數值y＞0;對稱軸為

跟蹤訓練9：已知關于x的不等式x2-ax-b＜0 的解集是(2,3),則a+b的值為( )。

A.-11 B.11

C.-1 D.1

提示：因為關于x的不等式x2-axb＜0的解集是(2,3),所以2,3 是方程x2-ax-b=0的根,所以a=5,b=-6。故a+b=-1。應選C。

題型十：一元二次不等式的恒成立問題

設f(x)=ax2+bx+c(a≠0),則f(x)＞0恒成立?a＞0 且Δ＜0;f(x)≥0恒成立?a＞0且Δ≤0;f(x)＜0恒成立?a＜0 且Δ＜0;f(x)≤0 恒成立?a＜0 且Δ≤0。若f(x)在定義域內存在最大值m,則f(x)＜a恒成立?a＞m;若f(x)在定義域內存在最大值m,則f(x)≤a恒成立?a≥m;若f(x)在定義域內存在最小值m,則f(x)＞a恒成立?a＜m;若f(x)在定義域內存在最小值m,則f(x)≥a恒成立?a≤m。在定義域D上,不等式f(x)＜m恒成立,則m＞f(x)max;不等式f(x)＜m能成立,則m＞f(x)min;不等式f(x)＞m恒成立,則m＜f(x)min;不等式f(x)＞m能成立,則m＜f(x)max。

例10(1)已知關于x的不等式ax2-2x+3a＜0在(0,2]上有解,則實數a的取值范圍是( )。

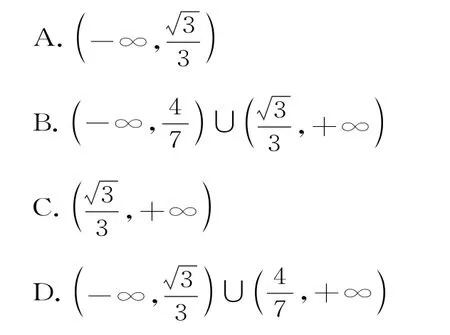
(2)若關于x的不等式2x2-8x-4+a≤0在1≤x≤3內有解,則實數a的取值范圍是( )。

A.a≤12 B.a≥12

C.a≤10 D.a≥10

(2)不等式2x2-8x-4+a≤0 在1≤x≤3內有解等價于a≤-2x2+8x+4 在1≤x≤3 內有解。設函數f(x)=-2x2+8x+4,x∈[1,3],則 原 問 題 等 價 于a≤f(x)max。又當x=2 時,f(x)max=12,所以a≤12。應選A。

跟蹤訓練10：若命題“存在x∈R,x2+(a-3)x+4＜0”為假命題,則實數a的取值范圍是_____。

提示：由題意可知,“對任意的x∈R,x2+(a-3)x+4≥0”為真命題,所以Δ=(a-3)2-16=a2-6a-7≤0,解得-1≤a≤7。故實數a的取值范圍是[-1,7]。

1.將一根鐵絲切割成三段,做一個面積為2m2,形狀為直角三角形的框架,在下列四種長度的鐵絲中,選用最合理(夠用且浪費最少)的是( )。

A.6.5m B.6.8m

C.7m D.7.2m

2.某公司一年需要購買某種原材料400t,計劃每次購買xt,已知運費為4萬元/次,一年總的庫存費用為4x萬元,為了使總的費用最低,每次購買的數量x為____。

提示:由題意得總的費用y=×4+,當且僅當x=20時取“=”。答案為20t。

說明：河南省教育科學規劃2023年度立項課題編號:2023YB0633 ;課題名稱:數學生成性教學對學生批判性思維能力的影響研究。