省間-省內(nèi)兩級(jí)市場(chǎng)協(xié)調(diào)下兩階段分布魯棒經(jīng)濟(jì)調(diào)度模型
陳 熠, 王 晗, 徐瀟源, 胡友琳, 嚴(yán) 正, 曾 丹, 馮 凱
(1. 上海交通大學(xué) 電力傳輸與功率變換控制教育部重點(diǎn)實(shí)驗(yàn)室,上海200240;2. 國網(wǎng)上海市電力公司 電力調(diào)度控制中心,上海200122;3. 中國電力科學(xué)研究院(南京分院),南京 210003)
我國70%以上的煤炭和水力資源集中在西部地區(qū),而電力負(fù)荷中心在中東部地區(qū),電力供應(yīng)資源與電力負(fù)荷需求逆向分布的特點(diǎn)決定了我國需要在全國范圍內(nèi)開展跨省電力輸送與電力交易,打破資源配置壁壘,實(shí)現(xiàn)更大范圍內(nèi)資源的優(yōu)化配置[1-2].為此,我國不斷深化電力市場(chǎng)改革,并逐步形成“統(tǒng)一市場(chǎng),兩級(jí)運(yùn)作”的電力市場(chǎng)框架.其中,“統(tǒng)一市場(chǎng)”強(qiáng)調(diào)實(shí)現(xiàn)電力資源在全國范圍內(nèi)優(yōu)化配置,“兩級(jí)運(yùn)作”強(qiáng)調(diào)省間電力市場(chǎng)與省內(nèi)電力市場(chǎng)協(xié)調(diào)運(yùn)行、聯(lián)合出清.與此同時(shí),為實(shí)現(xiàn)“碳達(dá)峰、碳中和”的目標(biāo),未來可再生能源接入電網(wǎng)的比例將不斷升高[3],可再生能源發(fā)電的間歇性將給電力系統(tǒng)的安全經(jīng)濟(jì)運(yùn)行帶來嚴(yán)峻挑戰(zhàn).在上述背景下,計(jì)及不確定性因素的影響,實(shí)現(xiàn)省間-省內(nèi)兩級(jí)市場(chǎng)運(yùn)作下電力系統(tǒng)的安全經(jīng)濟(jì)調(diào)度具有重要意義.
目前,不少學(xué)者已開展考慮“跨區(qū)跨省”電力傳輸與交易的電力系統(tǒng)經(jīng)濟(jì)調(diào)度模型研究.文獻(xiàn)[4]中提出考慮省間交易商的省間-省內(nèi)兩級(jí)電力市場(chǎng)最優(yōu)購電模型,有效降低市場(chǎng)運(yùn)行成本.文獻(xiàn)[5]中建立跨省區(qū)大電網(wǎng)安全約束經(jīng)濟(jì)調(diào)度模型,并采用優(yōu)化目標(biāo)和約束條件的靈活配置實(shí)現(xiàn)求解效率的提高.文獻(xiàn)[6]中提出跨省互聯(lián)電網(wǎng)雙級(jí)調(diào)度策略——日前調(diào)度制定機(jī)組啟停和跨省聯(lián)絡(luò)線輸電計(jì)劃;日內(nèi)調(diào)度根據(jù)實(shí)際光伏和負(fù)荷來調(diào)整機(jī)組出力和聯(lián)絡(luò)線輸電,提升系統(tǒng)運(yùn)行的經(jīng)濟(jì)性.文獻(xiàn)[7]中建立直流聯(lián)絡(luò)線功率階梯化運(yùn)行的模型,協(xié)調(diào)互補(bǔ)多個(gè)送端電網(wǎng)和受端電網(wǎng),促進(jìn)新能源的消納.文獻(xiàn)[8]中考慮送端儲(chǔ)能及功率跨區(qū)流動(dòng)狀態(tài),平抑送、受端交換功率的波動(dòng),充分發(fā)揮不同區(qū)域間的互濟(jì)效益.文獻(xiàn)[9]中提出轉(zhuǎn)供電力交易補(bǔ)償模型,能夠有效控制跨省電力交易的高運(yùn)行風(fēng)險(xiǎn)的線路.上述模型的構(gòu)建與求解為研究省間-省內(nèi)協(xié)調(diào)的電力系統(tǒng)經(jīng)濟(jì)調(diào)度問題奠定了基礎(chǔ).
上述文獻(xiàn)側(cè)重于跨區(qū)跨省電力系統(tǒng)經(jīng)濟(jì)調(diào)度模型構(gòu)建、跨區(qū)域輸電計(jì)劃制定的研究.隨著全國統(tǒng)一電力市場(chǎng)逐步建設(shè),省間市場(chǎng)和省內(nèi)市場(chǎng)協(xié)調(diào)運(yùn)作需求凸顯,省間-省內(nèi)兩級(jí)市場(chǎng)的協(xié)調(diào)運(yùn)作機(jī)制與模型受到廣泛關(guān)注,而如何在省間-省內(nèi)兩級(jí)市場(chǎng)協(xié)調(diào)運(yùn)作下實(shí)現(xiàn)日前-日內(nèi)兩階段的經(jīng)濟(jì)調(diào)度,目前研究尚不深入,需要進(jìn)一步探索可行的調(diào)度框架與建模方法.與此同時(shí),由于可再生能源發(fā)電比例不斷提高、電動(dòng)汽車等新興負(fù)荷大量接入,源-荷不確定性因素也將對(duì)省間-省內(nèi)兩級(jí)運(yùn)作的經(jīng)濟(jì)調(diào)度決策過程產(chǎn)生影響.2020年7月1日實(shí)施的《電力系統(tǒng)技術(shù)導(dǎo)則》明確指出電力系統(tǒng)應(yīng)充分考慮跨省跨區(qū)支援能力及新能源利用,以應(yīng)對(duì)新能源發(fā)電隨機(jī)性、間歇性的特征.針對(duì)源-荷不確定性因素,傳統(tǒng)電力系統(tǒng)優(yōu)化方法包括隨機(jī)優(yōu)化(Stochastic Optimization,SO)[10-11]和魯棒優(yōu)化(Robust Optimization,RO)[12-14],然而隨機(jī)優(yōu)化需要準(zhǔn)確獲取隨機(jī)變量的概率分布,且計(jì)算結(jié)果的樣本外表現(xiàn)不佳;魯棒優(yōu)化結(jié)果過于保守,影響系統(tǒng)運(yùn)行的經(jīng)濟(jì)性.近年來,不少學(xué)者提出分布魯棒優(yōu)化(Distributionally Robust Optimization, DRO)方法以彌補(bǔ)SO和RO的不足[15-17],為兩級(jí)市場(chǎng)協(xié)調(diào)運(yùn)作下研究含源-荷不確定性因素的日前-日內(nèi)兩階段經(jīng)濟(jì)調(diào)度問題提供了可行手段.
在省間-省內(nèi)兩級(jí)電力市場(chǎng)運(yùn)作框架下,計(jì)及源-荷不確定性因素的影響,提出一種不確定性環(huán)境下考慮省間-省內(nèi)兩級(jí)市場(chǎng)運(yùn)作的經(jīng)濟(jì)調(diào)度模型,包括日前調(diào)度和日內(nèi)調(diào)度兩個(gè)階段.在日前調(diào)度階段,以最小化省內(nèi)日前調(diào)度成本和省間購電成本為目標(biāo),構(gòu)建省間-省內(nèi)雙層日前經(jīng)濟(jì)調(diào)度模型;在日內(nèi)調(diào)度階段,以最小化省內(nèi)再調(diào)度成本為目標(biāo),建立考慮源-荷預(yù)測(cè)偏差的日內(nèi)備用調(diào)度模型.同時(shí),構(gòu)建范數(shù)距離模糊集用以刻畫源-荷預(yù)測(cè)偏差的不確定性,并提出雙層兩階段分布魯棒優(yōu)化方法,以實(shí)現(xiàn)上述模型的求解.最后,利用IEEE 39節(jié)點(diǎn)和118節(jié)點(diǎn)系統(tǒng)構(gòu)建多送端-多受端多省互聯(lián)的測(cè)試系統(tǒng),并利用算例仿真驗(yàn)證了所提模型及方法的有效性.
1 省間-省內(nèi)兩級(jí)電力市場(chǎng)下經(jīng)濟(jì)調(diào)度框架
我國各地的資源分布特點(diǎn)和電力供需差異造成不同區(qū)域間的電能輸送,也促進(jìn)了跨省電力交易的實(shí)施.然而,各區(qū)域輸電體系不同、各省市電價(jià)相差較大、各地域資源稟賦不同,因此在保障省內(nèi)電力供需平衡下如何實(shí)現(xiàn)電力資源在更大范圍內(nèi)的優(yōu)化配置是全國統(tǒng)一電力市場(chǎng)建設(shè)中需要解決的問題.為此,在全國統(tǒng)一電力市場(chǎng)體系頂層設(shè)計(jì)中提出符合我國實(shí)際情況的“統(tǒng)一市場(chǎng),兩級(jí)運(yùn)作”市場(chǎng)運(yùn)行方式.其中,兩級(jí)市場(chǎng)包括省間市場(chǎng)和省內(nèi)市場(chǎng),省間市場(chǎng)用于促進(jìn)跨省跨區(qū)間清潔能源的消納和大規(guī)模電力資源的配置;省內(nèi)市場(chǎng)用于保障省內(nèi)電力用戶需求,實(shí)現(xiàn)電力供需平衡[18].在此背景下,提出省間-省內(nèi)兩級(jí)電力市場(chǎng)運(yùn)作下日前-日內(nèi)兩階段經(jīng)濟(jì)調(diào)度框架(見圖1),旨在實(shí)現(xiàn)省間-省內(nèi)市場(chǎng)協(xié)調(diào)下的安全經(jīng)濟(jì)調(diào)度,保障區(qū)域資源的合理利用與省內(nèi)電力的供需平衡.
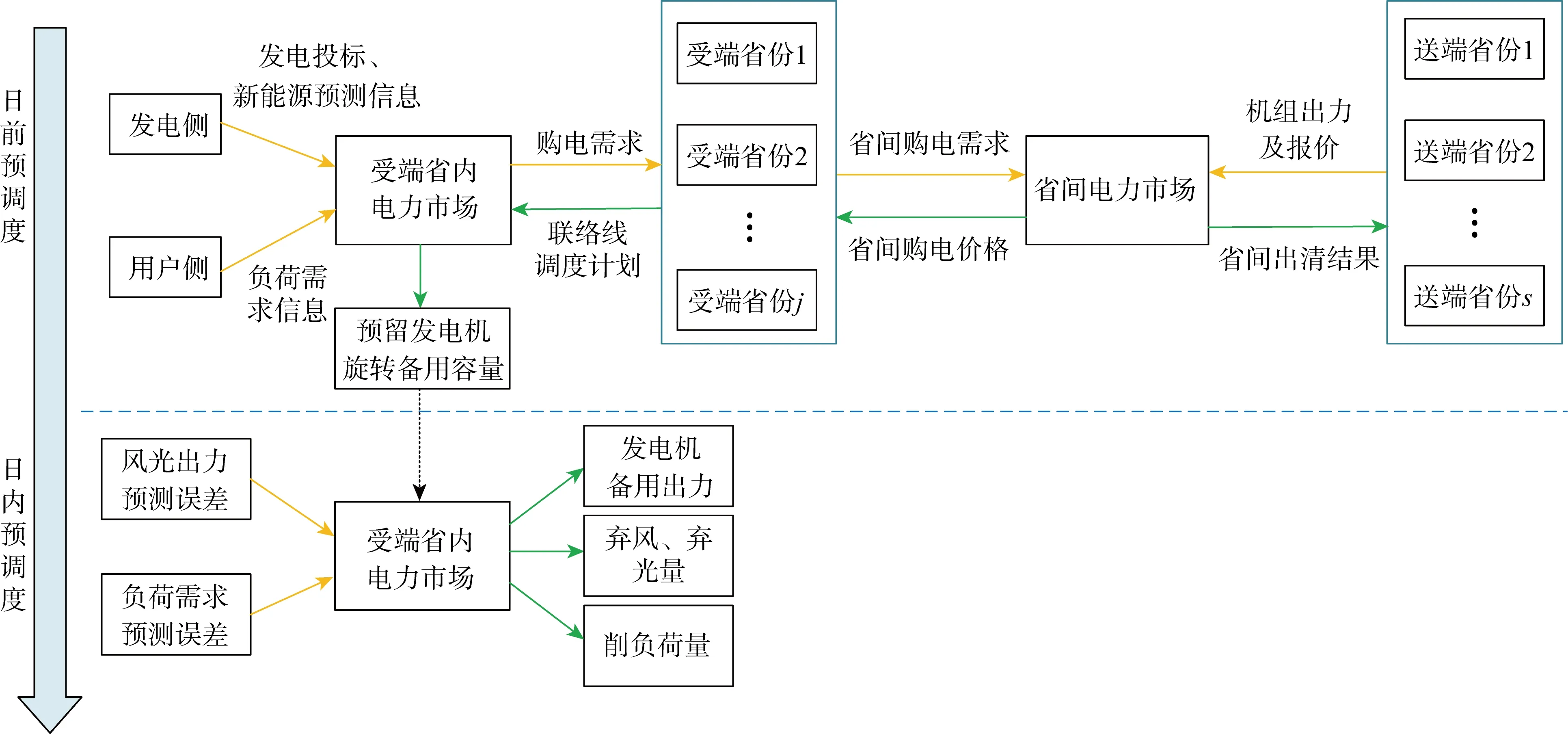
圖1 考慮省間-省內(nèi)兩級(jí)電力市場(chǎng)的日前-日內(nèi)兩階段經(jīng)濟(jì)調(diào)度框架Fig.1 Framework of inter-provincial and intra-provincial bi-level electricity market
1.1 日前調(diào)度
如圖1所示,在日前調(diào)度階段,首先,受端省份申報(bào)省間購電需求量,送端省份申報(bào)發(fā)電機(jī)組出力及報(bào)價(jià).根據(jù)受端和送端的申報(bào)信息,以最小化省間購電成本為目標(biāo),完成省間電力市場(chǎng)出清并得到省間聯(lián)絡(luò)線日前調(diào)度計(jì)劃.然后,各受端省份以省間聯(lián)絡(luò)線日前調(diào)度計(jì)劃為邊界條件,運(yùn)行省內(nèi)電力市場(chǎng),并根據(jù)省內(nèi)發(fā)電機(jī)組投標(biāo)、負(fù)荷需求和新能源預(yù)測(cè)出力信息,以最小化省內(nèi)市場(chǎng)運(yùn)作成本為目標(biāo),完成省內(nèi)市場(chǎng)出清.圖中黃色箭頭代表電力市場(chǎng)出清的輸入?yún)?shù),綠色箭頭代表市場(chǎng)出清結(jié)果,黑色虛線箭頭代表日前調(diào)度階段的出清結(jié)果作為輸入?yún)?shù)傳遞到日內(nèi)調(diào)度階段.
在省間-省內(nèi)兩級(jí)市場(chǎng)協(xié)調(diào)運(yùn)行中,省間市場(chǎng)出清后所得省間購電價(jià)格會(huì)影響受端省內(nèi)電力市場(chǎng)的出清結(jié)果,從而使得受端省份調(diào)整省間購電需求量并重新申報(bào).因此,需要省間-省內(nèi)多次迭代以獲得最優(yōu)省間購電需求和省間購電價(jià)格.在構(gòu)建模型時(shí),將省內(nèi)市場(chǎng)和省間市場(chǎng)分別作為模型的上、下層,上層模型傳遞省間購電需求給下層模型,下層模型傳遞省間購電價(jià)格給上層模型.在實(shí)際市場(chǎng)運(yùn)作過程中,可設(shè)置省間購電商以完成上述信息的傳遞[4].
1.2 日內(nèi)調(diào)度
如圖1所示,在日內(nèi)調(diào)度階段,市場(chǎng)主體為各受端省份,不涉及送端省份及省間市場(chǎng),送-受端聯(lián)絡(luò)線功率為日內(nèi)調(diào)度邊界條件.為了彌補(bǔ)風(fēng)光可再生能源出力和負(fù)荷需求的實(shí)際值與預(yù)測(cè)值之間的偏差,各受端省份采取發(fā)電機(jī)備用出力、棄風(fēng)棄光和削負(fù)荷措施,以保障電力供需平衡,應(yīng)對(duì)不確定性的影響.針對(duì)日內(nèi)調(diào)度階段可再生能源出力和負(fù)荷需求不確定性的影響,在后續(xù)模型的構(gòu)建中,采用基于1-范數(shù)和∞-范數(shù)的距離模糊集刻畫各典型隨機(jī)源-荷場(chǎng)景發(fā)生概率的不確定性,并在表征隨機(jī)源-荷預(yù)測(cè)偏差的不確定性后,利用分布魯棒優(yōu)化方法實(shí)現(xiàn)經(jīng)濟(jì)調(diào)度過程的建模.
所提出的日前-日內(nèi)兩階段經(jīng)濟(jì)調(diào)度框架能夠適應(yīng)省間-省內(nèi)兩級(jí)市場(chǎng)運(yùn)作流程,并通過發(fā)電機(jī)備用容量設(shè)置充分應(yīng)對(duì)新能源發(fā)電和負(fù)荷的不確定性,避免大量棄風(fēng)棄光和削負(fù)荷.
2 省間-省內(nèi)兩級(jí)市場(chǎng)協(xié)調(diào)運(yùn)行下經(jīng)濟(jì)調(diào)度模型
2.1 日前調(diào)度階段
2.1.1上層省內(nèi)模型 在日前調(diào)度階段,上層省內(nèi)模型的目標(biāo)是最小化省內(nèi)市場(chǎng)運(yùn)作成本,目標(biāo)函數(shù)為
(1)
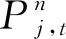
日前調(diào)度階段上層模型的約束條件如下.
(1) 省內(nèi)電力平衡約束:
?j∈J, ?t∈T
(2)
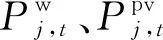
(2) 發(fā)電機(jī)出力約束:
(3)

(3) 發(fā)電機(jī)爬坡約束:
(4)
(4) 發(fā)電機(jī)備用容量約束:
(5)
(5) 線路潮流約束:
?j∈J, ?t∈T, ?l∈Lj
(6)
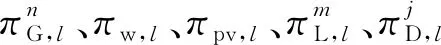
2.1.2下層省間模型 獲取省間購電需求量后,運(yùn)行省間電力市場(chǎng),并以最小化省間購電成本作為下層省間模型優(yōu)化的目標(biāo):
(7)
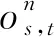
日前調(diào)度階段下層模型的約束條件如下.
(1) 省間聯(lián)絡(luò)線電力平衡約束:
?j∈J, ?t∈T
(8)
式中:ωs, j為第s個(gè)送端省份與第j個(gè)受端省份之間聯(lián)絡(luò)線的電力傳輸損耗系數(shù).
(2) 聯(lián)絡(luò)線傳輸容量約束:
?j∈J, ?s∈S, ?t∈T
(9)
式中:Cs,j,max、Cs,j,min分別為第s個(gè)送端省份與第j個(gè)受端省份之間聯(lián)絡(luò)線的傳輸容量上、下限.
(3) 送端省份發(fā)電機(jī)組容量約束:
?t∈T, ?s∈S, ?n∈Ns
(10)

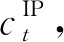
2.2 日內(nèi)調(diào)度階段
日內(nèi)調(diào)度階段需要根據(jù)新能源、負(fù)荷預(yù)測(cè)偏差進(jìn)行電力供需調(diào)整,包括省內(nèi)發(fā)電機(jī)組出力上調(diào)、下調(diào)和棄風(fēng)、棄光以及負(fù)荷削減.基于省內(nèi)市場(chǎng),日內(nèi)調(diào)度階段以省內(nèi)再調(diào)度成本最小為目標(biāo)函數(shù):
min(F1+F2)
(11)
式中:F1為日內(nèi)調(diào)度發(fā)電機(jī)上調(diào)和下調(diào)出力的成本;F2為棄風(fēng)、棄光和負(fù)荷削減的懲罰成本.F1和F2的表達(dá)式為
(12)
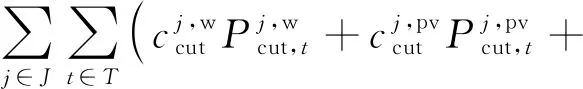
(13)
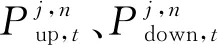
日內(nèi)調(diào)度階段的約束條件如下.
(1) 日內(nèi)調(diào)度電力平衡約束:
?j∈J, ?t∈T
(14)
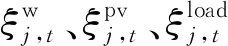
(2) 省內(nèi)機(jī)組出力調(diào)整和負(fù)荷削減約束:
(15)
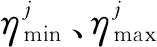
(3) 備用容量約束:
(16)
其中,日內(nèi)調(diào)度的可用容量受到日前調(diào)度預(yù)留備用容量的約束.
(4) 棄風(fēng)量、棄光量、負(fù)荷削減量約束:
(17)
式中:ηw、ηpv、ηload分別為最大棄風(fēng)量、棄光量和負(fù)荷削減量占比.
(5) 線路潮流約束:
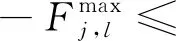
?j∈J, ?t∈T, ?l∈Lj
(18)
與日前調(diào)度階段相比,日內(nèi)調(diào)度階段只在受端省份的省內(nèi)市場(chǎng)之間進(jìn)行,并且受端省份之間設(shè)計(jì)了備用共享機(jī)制,即各受端省份共同享用所有的備用容量,各省間的備用電力可以相互傳遞.若出現(xiàn)一個(gè)受端省份新能源和負(fù)荷預(yù)測(cè)偏差波動(dòng)較大的情況,其余受端省份可以將省內(nèi)富余的備用電力輸送到該預(yù)測(cè)偏差波動(dòng)較大的省份.因此在備用共享機(jī)制下,單個(gè)省份的備用容量可以相對(duì)較少,各省可以共同面對(duì)新能源出力和負(fù)荷需求預(yù)測(cè)偏差不確定性的影響,從而有效減少備用容量總量.對(duì)于預(yù)測(cè)偏差帶來的不確定性因素,采用分布魯棒優(yōu)化方法進(jìn)行處理.
3 兩階段分布魯棒優(yōu)化調(diào)度模型構(gòu)建與求解
3.1 日前調(diào)度階段雙層模型的轉(zhuǎn)換
建立省間-省內(nèi)兩級(jí)市場(chǎng)協(xié)調(diào)運(yùn)行下日前-日內(nèi)經(jīng)濟(jì)調(diào)度模型,其中日前經(jīng)濟(jì)調(diào)度模型是一個(gè)雙層模型,包括上層省內(nèi)模型和下層省間模型,上層省內(nèi)模型的決策變量(省間購電需求)是下層省間模型的輸入,下層省間模型為線性規(guī)劃問題.針對(duì)該問題,可利用下層省間模型的Karush-Kuhn-Tucker (KKT)條件實(shí)現(xiàn)對(duì)下層省間模型的替換,從而將日前調(diào)度階段的雙層模型轉(zhuǎn)換成為單層模型[20].同時(shí),采用大M法對(duì)KKT條件中的互補(bǔ)松弛等式約束進(jìn)行線性化處理,并利用強(qiáng)對(duì)偶理論對(duì)目標(biāo)函數(shù)進(jìn)行線性化處理,從而將所得單層模型轉(zhuǎn)換為線性規(guī)劃問題[21],便于商業(yè)求解器實(shí)現(xiàn)快速求解.上述模型轉(zhuǎn)換的詳細(xì)過程參見附錄A.
3.2 日前-日內(nèi)兩階段分布魯棒優(yōu)化模型的構(gòu)建
相比于日前調(diào)度階段,日內(nèi)調(diào)度階段考慮了風(fēng)電、光伏和負(fù)荷的預(yù)測(cè)偏差,但實(shí)際運(yùn)行中新能源發(fā)電和負(fù)荷的預(yù)測(cè)偏差值存在不確定性,如何應(yīng)對(duì)上述不確定性因素的影響是需要解決的問題.目前,常用于處理不確定性因素的方法包括隨機(jī)優(yōu)化和魯棒優(yōu)化,但隨機(jī)優(yōu)化需要準(zhǔn)確獲取不確定性因素的概率分布信息,魯棒優(yōu)化所得優(yōu)化結(jié)果過于保守.近年來,分布魯棒優(yōu)化方法逐漸被采用,其結(jié)合了隨機(jī)優(yōu)化和魯棒優(yōu)化的特點(diǎn),既無需獲得準(zhǔn)確的概率分布信息,又克服魯棒優(yōu)化過于保守的缺點(diǎn),能夠?qū)崿F(xiàn)不確定性環(huán)境下的最優(yōu)決策.因此,引入分布魯棒優(yōu)化方法應(yīng)對(duì)日內(nèi)調(diào)度階段不確定性因素的影響.
分布魯棒優(yōu)化的核心在于構(gòu)建不確定性因素的概率分布模糊集,然后基于模糊集的表征方式計(jì)算最劣概率分布情況下的最優(yōu)決策結(jié)果.針對(duì)新能源發(fā)電和負(fù)荷預(yù)測(cè)偏差的不確定性,采用基于1-范數(shù)和∞-范數(shù)的距離信息模糊集實(shí)現(xiàn)不確定性表征.首先,對(duì)源-荷的歷史數(shù)據(jù)樣本進(jìn)行聚類處理[22],得到K個(gè)源-荷預(yù)測(cè)偏差典型場(chǎng)景以及各場(chǎng)景發(fā)生的概率pk(k= 1, 2, …,K);然后,構(gòu)建基于1-范數(shù)和∞-范數(shù)的模糊集來刻畫上述K個(gè)典型場(chǎng)景可能出現(xiàn)概率的不確定性;最后,完成隨機(jī)源-荷預(yù)測(cè)偏差的表征.上述過程中,基于1-范數(shù)距離和∞-范數(shù)距離所構(gòu)建的模糊集如下:
Ω1=
(19)
Ω∞=
(20)
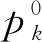
根據(jù)文獻(xiàn)[16]可知,{pk}中所有的元素滿足如下置信度約束:
(21)
式中:Pr{·}為滿足條件“·”的概率;M為樣本規(guī)模.
當(dāng)式(21)不等式右邊的置信度分別設(shè)置為α1和α∞時(shí),可得到:
(22)
利用式(22),在實(shí)際優(yōu)化計(jì)算中便可通過設(shè)置置信度參數(shù)α1和α∞來確定模糊集中的允許偏差上限值θ1和θ∞.
在形成表征源-荷預(yù)測(cè)偏差不確定性的模糊集后,將源-荷預(yù)測(cè)偏差作為隨機(jī)變量,在日前階段模型所轉(zhuǎn)化的單層模型基礎(chǔ)上,構(gòu)建如下緊湊形式的日前-日內(nèi)兩階段分布魯棒經(jīng)濟(jì)調(diào)度模型:
(23)
s.t.Ax≤c
(24)
Bx+Cyk+Dξk≤d
(25)
Ex+Fyk≤e
(26)
x≥0,yk≥0
(27)
式中:pk為第k個(gè)源-荷預(yù)測(cè)偏差不確定性場(chǎng)景發(fā)生的概率;x和y分別為日前調(diào)度階段和日內(nèi)調(diào)度階段的決策變量,其中日前調(diào)度階段模型已轉(zhuǎn)換為單層模型;yk為第k個(gè)源-荷預(yù)測(cè)偏差場(chǎng)景下的日內(nèi)調(diào)度階段的決策變量;ξk為表征第k個(gè)源-荷預(yù)測(cè)偏差場(chǎng)景下風(fēng)電、光伏和負(fù)荷預(yù)測(cè)偏差值的隨機(jī)變量;Ω為源-荷預(yù)測(cè)偏差場(chǎng)景概率取值的可行域;X為x的可行域;Y(x,ξk)為第k個(gè)源-荷預(yù)測(cè)偏差場(chǎng)景下yk的可行域;a~e、A~F分別在緊湊形式中代表向量和矩陣.
式(23)為日前-日內(nèi)兩階段分布魯棒優(yōu)化目標(biāo)函數(shù)的緊湊形式,對(duì)應(yīng)式(A10)和式(11);約束式(24)對(duì)應(yīng)約束式(2)~(6)、(A2)~(A3)和(A5)~(A6);約束式(25)對(duì)應(yīng)約束式(14)、(15)和(18);約束式(26)對(duì)應(yīng)約束式(16)和(17).
3.3 日前-日內(nèi)兩階段分布魯棒優(yōu)化模型的求解
采用采用列約束生成(Column Constraint Generation, CCG)算法[23]實(shí)現(xiàn)兩階段分布魯棒優(yōu)化模型的求解.該算法將原模型分解成主問題(MP)和子問題(SP),MP和SP分別給式(23)定義上界和下界,并利用主-子問題間的反復(fù)迭代實(shí)現(xiàn)模型求解,求解流程如圖2所示,所需要迭代求解的主問題和子問題如下.
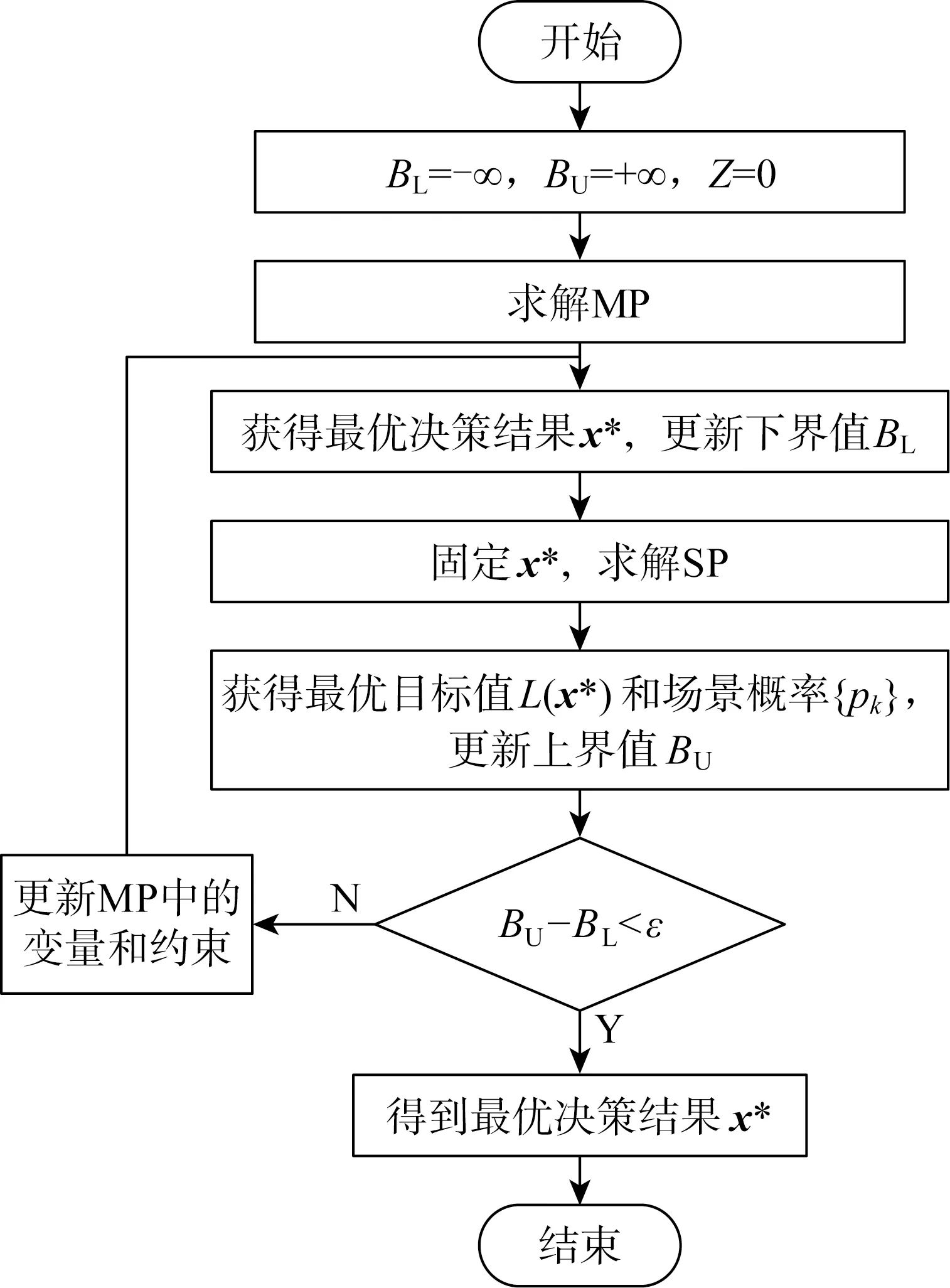
圖2 CCG算法求解流程圖Fig.2 Flow chart of CCG algorithm
(1) 主問題(MP):
(28)
(29)
式中:G為最大值;Z為迭代次數(shù).
求解主問題得到日前調(diào)度階段最優(yōu)決策結(jié)果x*,并更新下界值BL,即
BL=max{BL,aTx*+G}
(30)
(2) 子問題(SP):
(31)
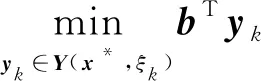
(32)
式(32)求解完成后更新上界值,即
BU=min{BU,aTx*+G(x*)}
(33)

4 算例仿真
4.1 算例設(shè)置
采用IEEE 39節(jié)點(diǎn)和118節(jié)點(diǎn)系統(tǒng)進(jìn)行算法仿真,系統(tǒng)數(shù)據(jù)參見文獻(xiàn)[24].其中,39節(jié)點(diǎn)和118節(jié)點(diǎn)系統(tǒng)分別作為受端省份A省、B省,并分別接入1個(gè)新能源風(fēng)光電廠,風(fēng)力和光伏發(fā)電均接入同一個(gè)節(jié)點(diǎn);分別設(shè)置3個(gè)送端省份C省、D省和E省參與省間市場(chǎng).送端和受端省份的劃分考慮水電、新能源等電力富足省份向負(fù)荷中心省份的電力輸送行為,并且以省間聯(lián)絡(luò)線作為劃分邊界.送端-受端的電網(wǎng)傳輸結(jié)構(gòu)圖如圖3所示,新能源電站和送端-受端聯(lián)絡(luò)線的接入位置如表1所示;受端省份省間聯(lián)絡(luò)線分別接于A省節(jié)點(diǎn)30和B省節(jié)點(diǎn)58;參與省間市場(chǎng)的機(jī)組容量、報(bào)價(jià)以及跨省聯(lián)絡(luò)線線損率如附錄B所示;電力傳輸損耗系數(shù)參見文獻(xiàn)[4].根據(jù)受端A省和B省的新能源出力及負(fù)荷的歷史預(yù)測(cè)數(shù)據(jù)和實(shí)際數(shù)據(jù),利用K-means算法聚類處理,分別得到受端A、B兩省的3個(gè)預(yù)測(cè)誤差典型場(chǎng)景,如圖4所示.此外,測(cè)試環(huán)境為Intel Core i7-8550四核CPU,16 GB內(nèi)存,使用MATLAB R2020b編譯和測(cè)試.

表1 新能源電廠和省間聯(lián)絡(luò)線接入點(diǎn)位置
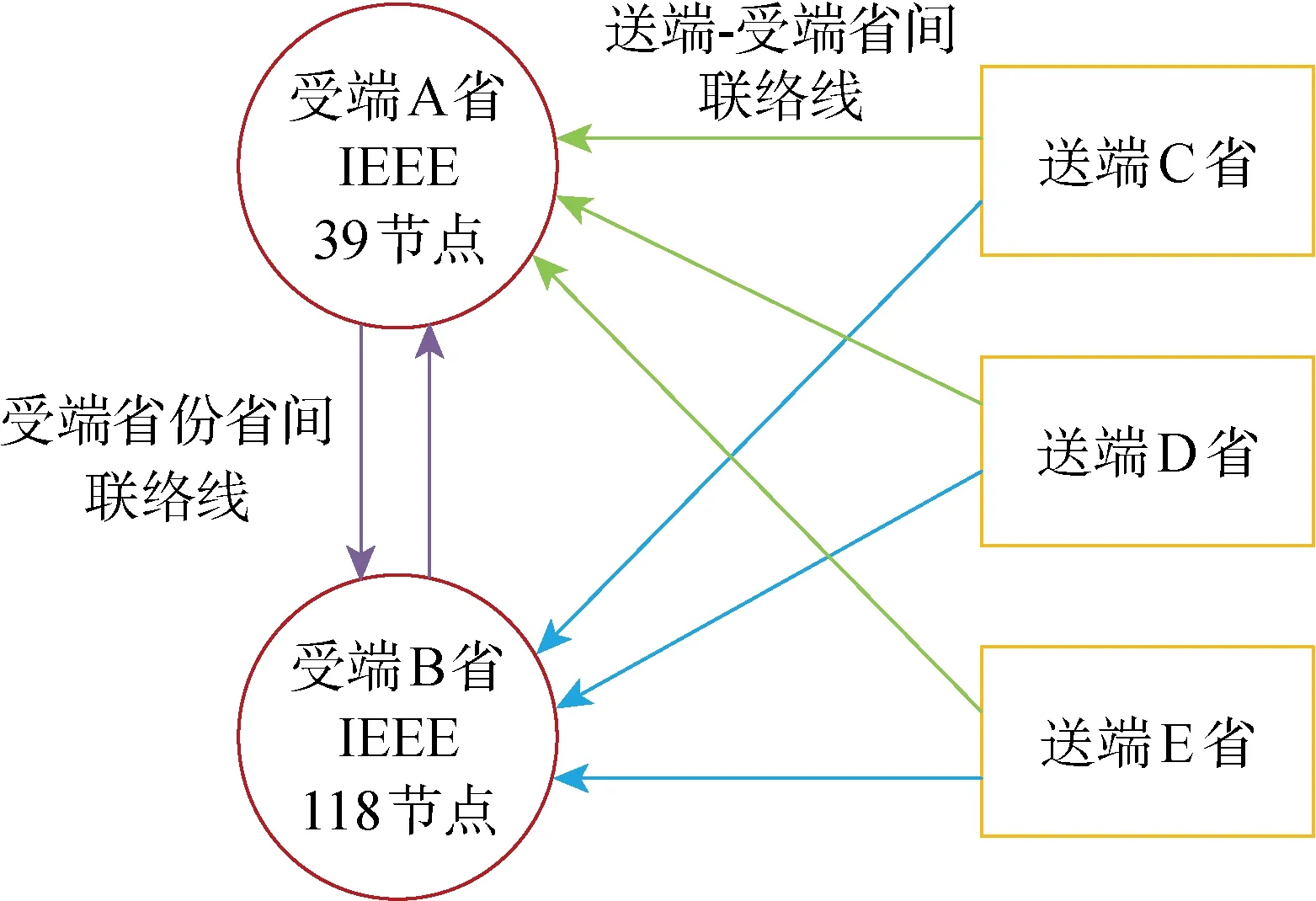
圖3 送端-受端電網(wǎng)結(jié)構(gòu)圖Fig.3 Structure diagram of sending and receiving power grids

圖4 受端A省、B省源-荷預(yù)測(cè)偏差場(chǎng)景及概率Fig.4 Scenarios and probability of source-load with forecast errors in receiving provinces A and B
4.2 日前調(diào)度結(jié)果
4.2.1日前調(diào)度階段成本分析 基于所提模型和求解方法,優(yōu)化求解日前調(diào)度階段省內(nèi)發(fā)電、省間購電和日前調(diào)度備用成本如表2所示.由于受端省份B總負(fù)荷高于受端省份A且B省發(fā)電機(jī)成本系數(shù)高于A省,所以B省的省內(nèi)發(fā)電成本和省間購電成本都高于A省.然而,B省新能源及負(fù)荷預(yù)測(cè)誤差較小,所以其備用成本低于A省.圖5進(jìn)一步給出A省日前調(diào)度階段各個(gè)發(fā)電機(jī)的出力情況.其中,發(fā)電機(jī)1、2 的發(fā)電成本較低,在日前調(diào)度階段為A省負(fù)荷的主要承擔(dān)者;發(fā)電機(jī)4~10的發(fā)電成本較高,基本均保持在最小機(jī)組出力.省內(nèi)發(fā)電機(jī)的日前調(diào)度結(jié)果是綜合考慮備用成本、省間購電成本以及用于應(yīng)對(duì)源-荷預(yù)測(cè)偏差而產(chǎn)生的日內(nèi)調(diào)度成本而得到的.
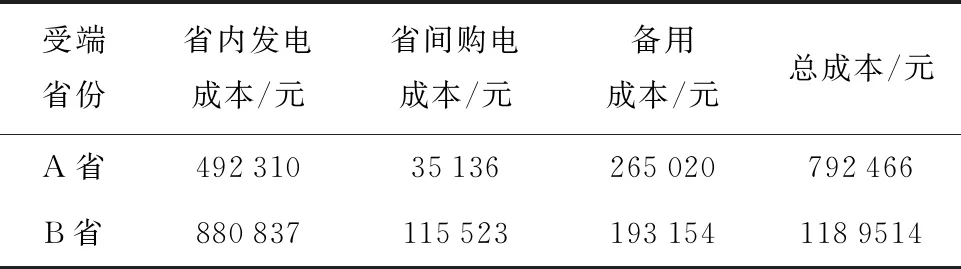
表2 日前調(diào)度階段成本Tab.2 Cost in day-ahead dispatch stage

圖5 受端A省日前調(diào)度階段發(fā)電機(jī)出力Fig.5 Generator outputs of receiving end A in day-ahead dispatch stage
4.2.2省間市場(chǎng)購電行為分析 圖6為受端省份A、B在省間市場(chǎng)的購電情況,根據(jù)電力市場(chǎng)出清準(zhǔn)則,即滿足最大化社會(huì)福利的目標(biāo),只有當(dāng)省間購電價(jià)格低于省內(nèi)發(fā)電機(jī)組邊際電價(jià)時(shí),省間購電交易才會(huì)發(fā)生,整體社會(huì)福利才會(huì)增加.結(jié)合附錄B中圖B1所示的凈負(fù)荷曲線可知,中午12時(shí)A、B省的凈負(fù)荷,即負(fù)荷與新能源出力的差值均增加,而A省邊際發(fā)電機(jī)組的邊際價(jià)格17.3 美元/MW高于B省邊際發(fā)電機(jī)組的邊際價(jià)格16.9 美元/MW,且均高于省間購電價(jià)格16.2 美元/MW,這使得D、E省至A省的省間購電量顯著增加、至B省的省間購電量顯著減少(12時(shí)為0).晚上21時(shí),由于新能源出力減少、負(fù)荷增加導(dǎo)致系統(tǒng)凈負(fù)荷增大,此時(shí)省間購電量也達(dá)到峰值,A、B省大部分機(jī)組的邊際價(jià)格均大于省間購電價(jià)格16.9 美元/MW.值得注意的是,C省的外送電量均傳輸?shù)紹省,這是由于C省本身存在發(fā)電成本較低的機(jī)組,同時(shí)在不考慮省間購電時(shí)B省的邊際電價(jià)高于A省,所以在凈負(fù)荷較低時(shí)(如0—6時(shí))B省均存在省間購電,C省外送電量也優(yōu)先支持B省用電,以降低系統(tǒng)運(yùn)行總成本.
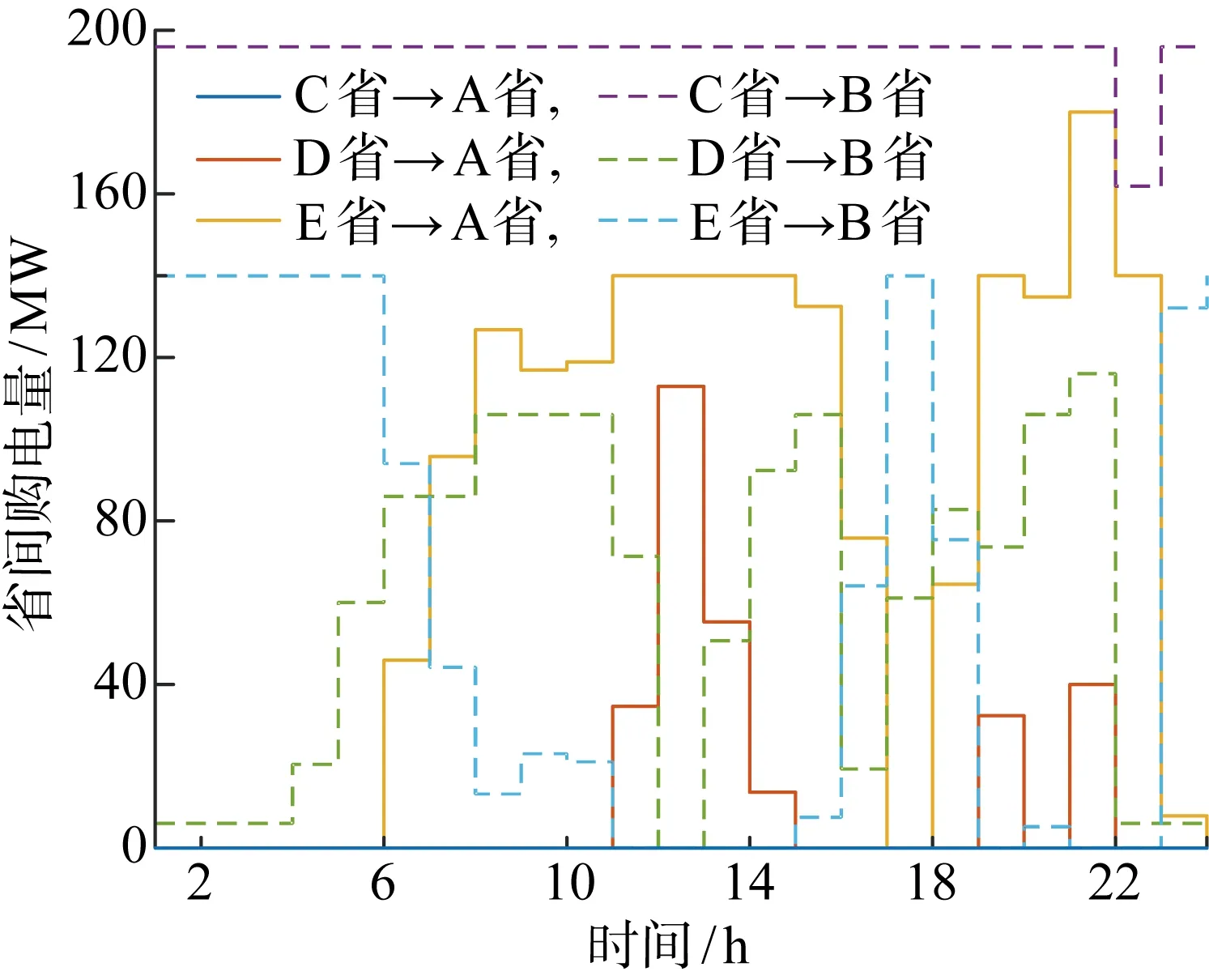
圖6 受端A省、B省的省間購電量Fig.6 Inter-provincial power purchase of receiving provinces A and B
4.2.3省內(nèi)線路阻塞分析 調(diào)整受端省份A、B省內(nèi)線路容量上限值,A省內(nèi)線路容量由500 MW降低為400 MW,B省內(nèi)線路容量由500 MW降低為450 MW.降低線路容量上限值后,A省、B省會(huì)發(fā)生線路阻塞,阻塞情況下目標(biāo)函數(shù)與未阻塞情況下的目標(biāo)函數(shù)相同,只是線路潮流約束更為嚴(yán)格,參照式(1)分別計(jì)算線路阻塞與未阻塞情況下系統(tǒng)的發(fā)電成本和購電成本,如表3所示.總體而言,發(fā)生阻塞之后A、B兩省的發(fā)電成本與購電成本之和略有增加.其中,線路阻塞導(dǎo)致A省的邊際電價(jià)增加并高于B省的邊際電價(jià),從而使得B省的省間購電量降低,A省的省間購電量增加,并表現(xiàn)為A省阻塞情況下的省內(nèi)發(fā)電成本略低于未阻塞情況下的成本,B省阻塞情況下的省間購電成本略低于未阻塞情況下的成本.
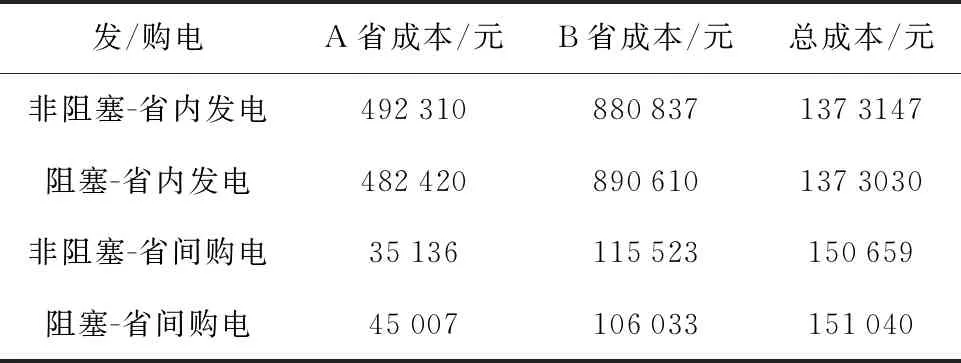
表3 阻塞與未阻塞時(shí)A、B省的發(fā)電、購電成本
圖7具體給出A、B省在阻塞與非阻塞情況下的省間購電量.在線路阻塞情況下,11—15時(shí)和19—22時(shí)D省向A省的輸電量大于非阻塞時(shí)向A省的輸電量,6—10、15—18、20和23時(shí)E省向A省的輸電量大于非阻塞時(shí)向A省的輸電量,且在12、22時(shí)C省也向A省外送輸電.
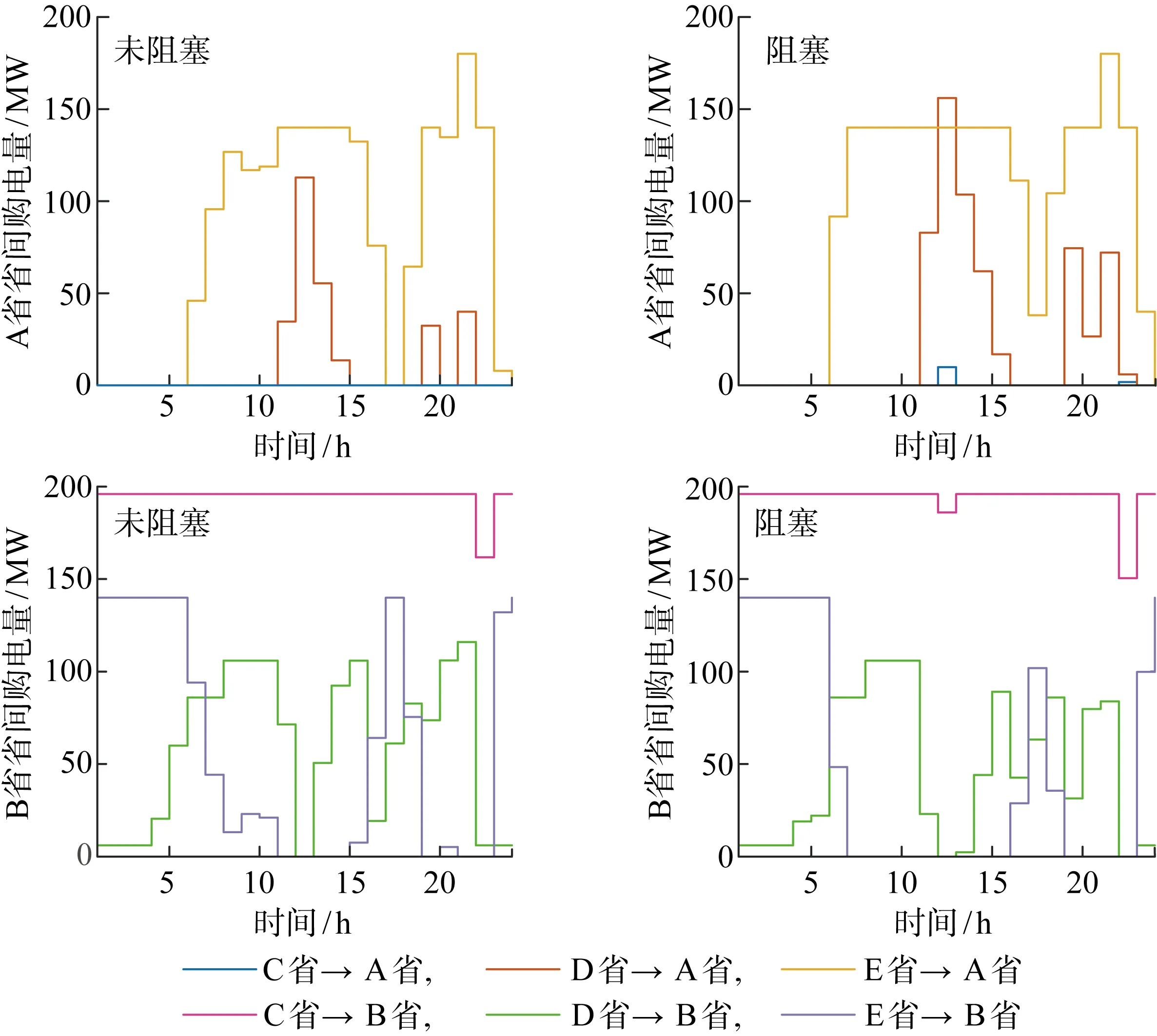
圖7 阻塞與未阻塞時(shí)省間購電量對(duì)比Fig.7 Comparison of inter-provincial power purchase in congestion and non-congestion scenarios
4.3 日內(nèi)調(diào)度結(jié)果
4.3.1DRO方法分析 考慮源-荷預(yù)測(cè)偏差的不確定性,分別設(shè)定1-范數(shù)和∞-范數(shù)的置信度α1=0.5,α∞=0.5,利用所提雙層兩階段分布魯棒優(yōu)化方法求解,所得結(jié)果與傳統(tǒng)SO、RO對(duì)比,如表4所示.由表4結(jié)果可知,基于DRO(1-范數(shù)和∞-范數(shù))所得日內(nèi)調(diào)度總成本略高于SO所得總成本,且遠(yuǎn)低于RO所得總成本.DRO方法避免了RO方法所得結(jié)果過于保守的缺點(diǎn),又保持了SO方法經(jīng)濟(jì)性的特點(diǎn).
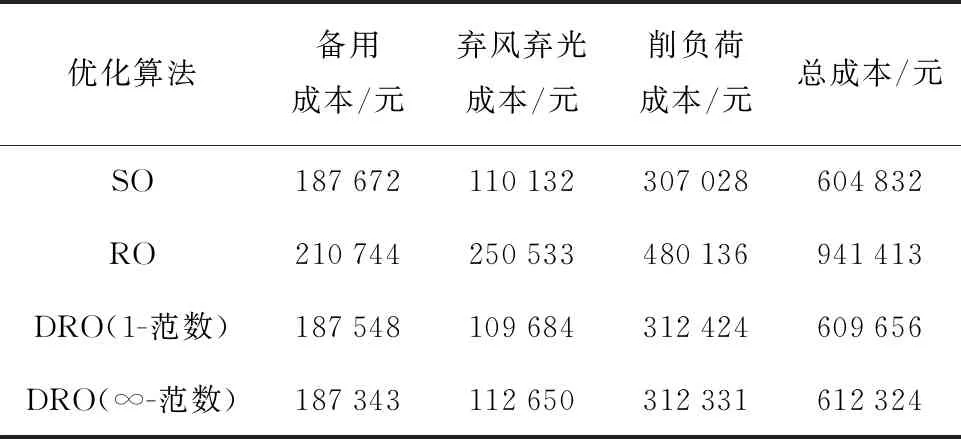
表4 SO、RO與DRO方法結(jié)果對(duì)比Tab.4 Comparison of SO, RO, and DRO results
為對(duì)比DRO和SO的樣本外表現(xiàn),先根據(jù)給定典型場(chǎng)景樣本計(jì)算出第一階段日前調(diào)度決策變量,然后重新隨機(jī)生成新的場(chǎng)景,并進(jìn)行第二階段日內(nèi)調(diào)度優(yōu)化計(jì)算,總成本如表5所示.可以發(fā)現(xiàn),SO計(jì)算結(jié)果的平均值低于DRO計(jì)算結(jié)果的平均值,但是SO計(jì)算結(jié)果的標(biāo)準(zhǔn)差大于DRO計(jì)算結(jié)果的標(biāo)準(zhǔn)差,波動(dòng)幅度較大.SO最大值的情況出現(xiàn)在新能源波動(dòng)性較大導(dǎo)致機(jī)組備用不能平衡新能源波動(dòng),此時(shí)被迫需要削負(fù)荷或棄風(fēng)棄光,使得運(yùn)行成本大大增加.相比于SO,DRO在日前調(diào)度階段保留更為充足的機(jī)組備用,能夠在日內(nèi)調(diào)度階段更有效地面對(duì)新能源不確定性的波動(dòng),削負(fù)荷和棄風(fēng)棄光的量較少,總成本波動(dòng)較小,樣本外表現(xiàn)結(jié)果具有魯棒性較好的特征.
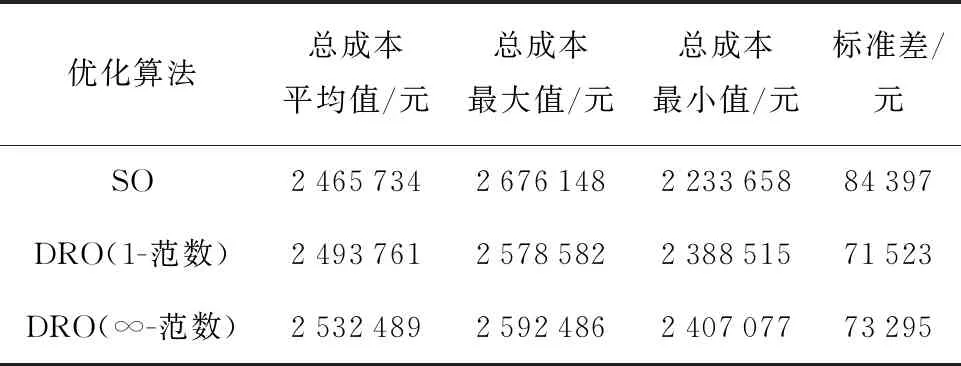
表5 SO與DRO方法樣本外結(jié)果對(duì)比Tab.5 Comparison of SO and DRO out-of-sample results
由式(22)可知,置信度α1、α∞不同,則DRO方法中允許偏差上限值θ1、θ∞不同,選取不同的α1、α∞,對(duì)比分析其對(duì)雙層兩階段經(jīng)濟(jì)調(diào)度結(jié)果的影響.如表6所示,對(duì)于1-范數(shù)和∞-范數(shù),置信度越高,兩階段經(jīng)濟(jì)調(diào)度的總成本越高.此外,可設(shè)置不同的置信度來調(diào)整計(jì)算結(jié)果的魯棒性,置信度越高,所得結(jié)果魯棒性越強(qiáng).當(dāng)置信度α1、α∞相同時(shí),采用∞-范數(shù)所得總成本高于采用1-范數(shù)的結(jié)果,說明∞-范數(shù)下調(diào)度結(jié)果較1-范數(shù)更為保守.
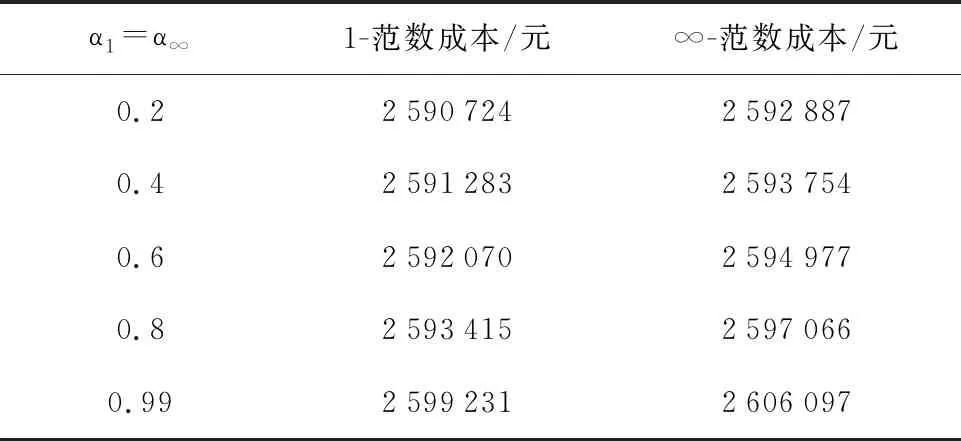
表6 1-范數(shù)與∞-范數(shù)結(jié)果對(duì)比Tab.6 Comparison of results with 1-norm and ∞-norm
4.3.2受端省份日內(nèi)備用共享情況 選取圖4中源-荷預(yù)測(cè)偏差概率最大的場(chǎng)景(A省-場(chǎng)景1、B省-場(chǎng)景3),分別計(jì)算受端省份A、B間的備用共享情況,所得結(jié)果如圖8所示.由圖可見,B省在場(chǎng)景3下的預(yù)測(cè)偏差波動(dòng)較大,為降低B省內(nèi)發(fā)電機(jī)上/下調(diào)、棄風(fēng)/棄光以及削負(fù)荷的成本,利用A省富余的備用容量平抑B省的源-荷預(yù)測(cè)偏差,實(shí)現(xiàn)備用共享,能夠提升系統(tǒng)整體經(jīng)濟(jì)性.
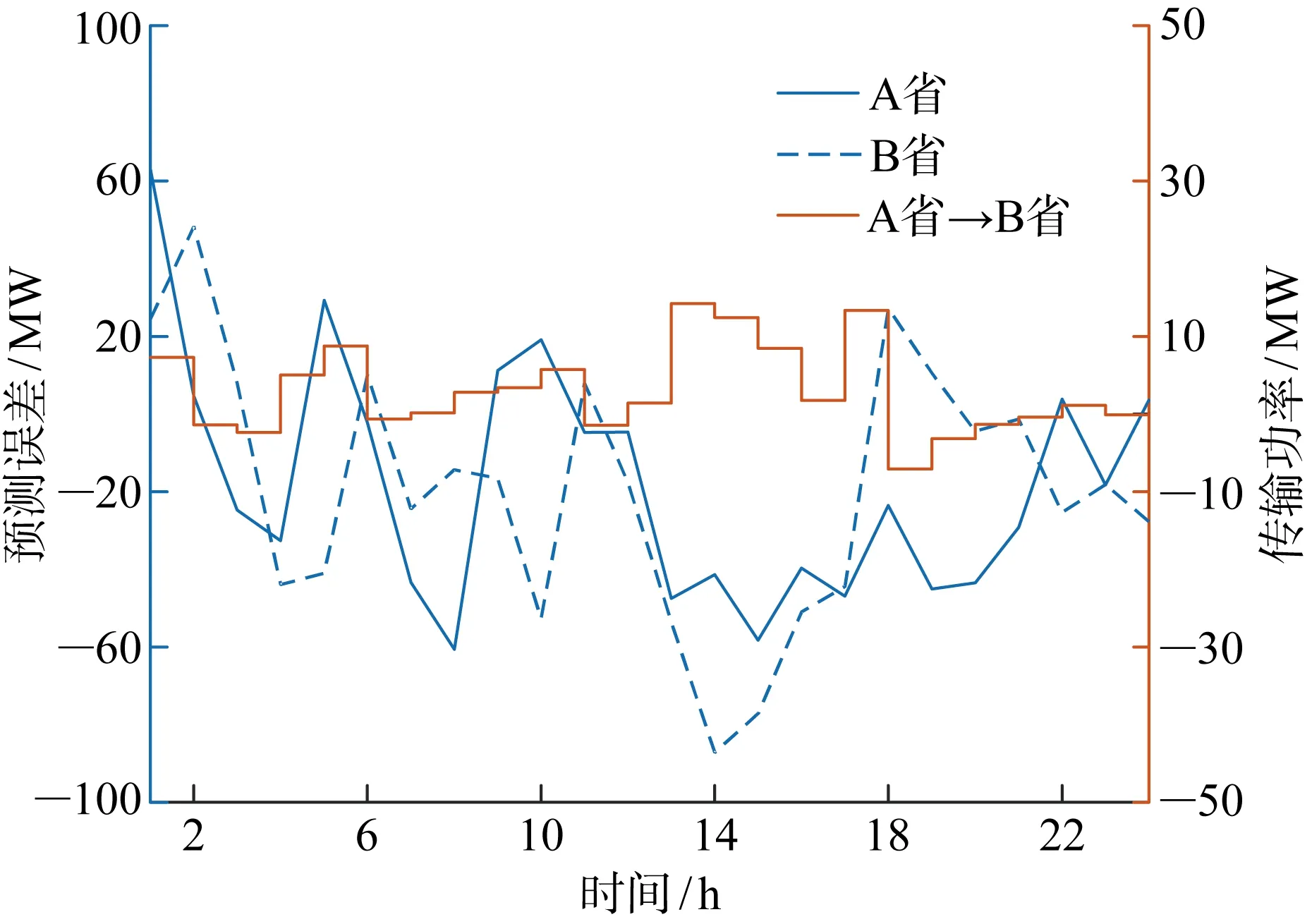
圖8 受端A省、B省源-荷預(yù)測(cè)偏差及傳輸功率Fig.8 Forecast errors of source-load and transmission power between receiving provinces A and B
5 結(jié)論
基于我國省間-省內(nèi)兩級(jí)電力市場(chǎng)運(yùn)作現(xiàn)狀,充分考慮新能源和負(fù)荷不確定性的影響,提出一種不確定性環(huán)境下考慮省間-省內(nèi)兩級(jí)市場(chǎng)運(yùn)作的兩階段經(jīng)濟(jì)調(diào)度模型,并得到以下結(jié)論.
(1) 利用范數(shù)距離(1-范數(shù)和∞-范數(shù))模糊集有效刻畫不確定性源-荷預(yù)測(cè)偏差,建立雙層兩階段分布魯棒優(yōu)化模型,利用KKT條件轉(zhuǎn)換和CCG算法迭代求解,有效實(shí)現(xiàn)不確定性環(huán)境下考慮省間-省內(nèi)兩級(jí)市場(chǎng)運(yùn)作的電力系統(tǒng)經(jīng)濟(jì)調(diào)度,驗(yàn)證了DRO方法相對(duì)于SO和RO方法的優(yōu)點(diǎn).
(2) 省間-省內(nèi)兩級(jí)電力市場(chǎng)運(yùn)作下的兩階段經(jīng)濟(jì)調(diào)度模型具有如下特點(diǎn):在日前調(diào)度階段,省間市場(chǎng)的存在有效降低省內(nèi)市場(chǎng)的運(yùn)行成本,且能夠有效緩解省內(nèi)線路阻塞所引起的運(yùn)行成本增加的問題;在日內(nèi)調(diào)度階段,受端省份間的備用共享機(jī)制提升受端省份共同應(yīng)對(duì)新能源和負(fù)荷預(yù)測(cè)偏差的能力,有助于降低日內(nèi)再調(diào)度成本.
未來將研究虛擬電廠對(duì)兩級(jí)電力市場(chǎng)的影響,并研究儲(chǔ)能在兩級(jí)市場(chǎng)環(huán)境下對(duì)平抑新能源波動(dòng)性的作用.
附錄見本刊網(wǎng)絡(luò)版(xuebao.sjtu.edu.cn/article/2023/1006-2467-57-09-1114.shtml)

