淺談電磁場理論中梯度、散度和旋度的教學(xué)

吳微微 徐延林 何 艷

國防科技大學(xué)電子科學(xué)學(xué)院 湖南長沙 410073

一、概述

麥克斯韋以一種近乎完美的方式統(tǒng)一了電和磁,形成一門獨立的學(xué)科——電磁學(xué)。同時,預(yù)言了電磁波的存在,這是物理學(xué)家在統(tǒng)一之路上的巨大進(jìn)步。若從微觀角度探究電磁場的特性,需將宏觀中的有向曲線、有向曲面以及由封閉曲面圍成的體積無限縮小至趨于零的程度,用電磁場的散度和旋度等物理量代替宏觀中的通量、環(huán)量等物理量進(jìn)行研究。標(biāo)量場的梯度、矢量場的散度及其旋度的計算離不開符號簡化史上一個奇跡——哈密頓算子(?算子)。教學(xué)實施過程中發(fā)現(xiàn),當(dāng)從宏觀角度轉(zhuǎn)向微觀角度探究電磁場特性時,學(xué)生們理解起來有不小的難度。例如,在電磁場理論中,如何理解自帶方向的哈密頓算子的物理意義?除了用于計算,梯度、散度和旋度的物理意義是什么?本文將通過三個模型,詳細(xì)闡釋哈密頓算子、梯度、散度和旋度的物理意義,便于學(xué)生掌握微分形式麥克斯韋方程組的核心內(nèi)容。

二、哈密頓算子的解讀

為了簡化電磁場理論中的運算,英國數(shù)學(xué)家、物理學(xué)家和力學(xué)家威廉·羅恩·哈密頓引出了倒三角符號?,因此得名哈密頓算子,它是場論分析中不可或缺的工具。它是一個同時具有矢量和微分雙重特性的矢量算子,主要研究場量在空間中的變化。要理解哈密頓算子,需要從描述函數(shù)f變化快慢的概念——導(dǎo)數(shù)說起。當(dāng)函數(shù)f的變化與時間有關(guān),則記為f(t)。描述該函數(shù)增量與自變量—時間增量之間比值的函數(shù)為g(t)=Δf(t)/Δt。例如,當(dāng)f(t)為距離時,則g(t)為速度;當(dāng)f(t)為速度時,g(t)為加速度。當(dāng)f(t)為一條隨時間變化的曲線時,f(t)的增量Δf(t)與其微分df(t)之間的關(guān)系如圖1所示。

圖1中,時間軸上的增量為Δt,其微分為dt,兩者大小相等。增量Δy表示時間上增加Δt時函數(shù)f(t)的增量,它是函數(shù)f(t)的實際變化量Δf(t)=Δy。當(dāng)在P點做一條切線,以直線代替曲線,則當(dāng)時間軸上變化了Δt,直線上對應(yīng)

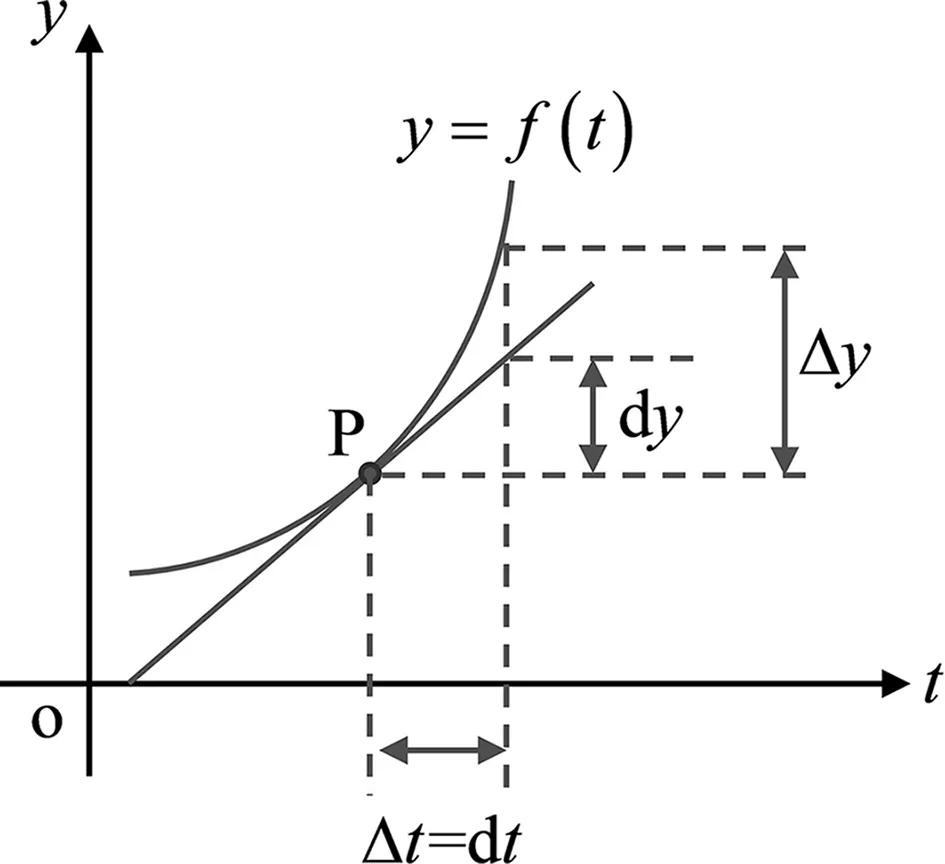
圖1 函數(shù)f(t)的增量Δy與微分dy的關(guān)系

的變化即為微分df(t)=dy,微分dy為增量Δy的線性主部。這種“以直(dy)代曲Δy”是現(xiàn)代微積分的一個核心思想,利用P點處的導(dǎo)數(shù)dy/dt就可以表示該點處函數(shù)隨時間變化的快慢。若想研究該函數(shù)f(t)在空間中某一點上隨空間變化的快慢,需首先選擇一個坐標(biāo)系并進(jìn)行研究。為簡單起見,本文選擇直角坐標(biāo)系進(jìn)行研究,詮釋哈密頓算子的物理意義。將函數(shù)f(t)的自變量由時間變量t改為直角坐標(biāo)系中任意一個軸向,如x軸,則導(dǎo)數(shù)dy/dx研究的是函數(shù)y=f(x)在空間中沿x軸方向的變化率。若想同時研究P(x0,y0,z0)點處,函數(shù)f(x,y,z)沿三個坐標(biāo)軸方向的空間變化率,則需利用偏導(dǎo)數(shù)分別研究各個方向上的空間變化率。首先,固定該點在y軸和z軸上的位置y=y0和z=z0,研究函數(shù)f(x,y0,z0)沿x軸方向的變化率:

(1)

同理,可得到沿另外兩個方向的變化率。若想同時表示空間P(x0,y0,z0)點在三個坐標(biāo)軸方向上的空間變化率,則需將三個方向上的變化率分別用相對應(yīng)的單位矢量進(jìn)行標(biāo)記后相加即可。

但由于將三個方向上的變化率用類似公式(1)的方式表示出來時,雖然概念清晰,但十分冗長。于是,哈密頓提出一種矢量算子簡化上述表示式,得到如下簡潔形式:

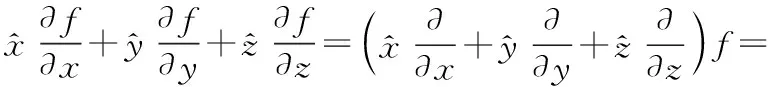
(2)

綜上所述,哈密頓算子的物理意義是研究一個空間分布函數(shù)f(x,y,z),沿三個坐標(biāo)軸方向各自的空間變化率。

三、梯度模型

在電磁場理論中,標(biāo)量場的梯度和矢量場的散度及旋度的物理意義一直是教學(xué)的重點和難點。基于上一小節(jié)闡釋哈密頓算子物理意義的過程,用于研究標(biāo)量場的梯度的物理意義躍然紙上。設(shè)標(biāo)量場函數(shù)f(x,y)的空間自變量為x和y,如圖2所示。在空間位置點P(x0,y0)處的梯度表明了該函數(shù)f(x,y)在此點處沿x和y方向增加率最快最大的方向,由圖2中箭頭所示。圖3為函數(shù)f(x,y)投影到xoy平面上的情況。

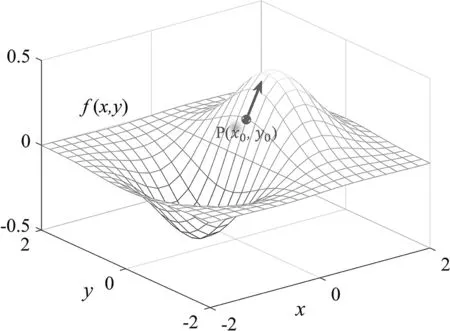
圖2 標(biāo)量場的梯度

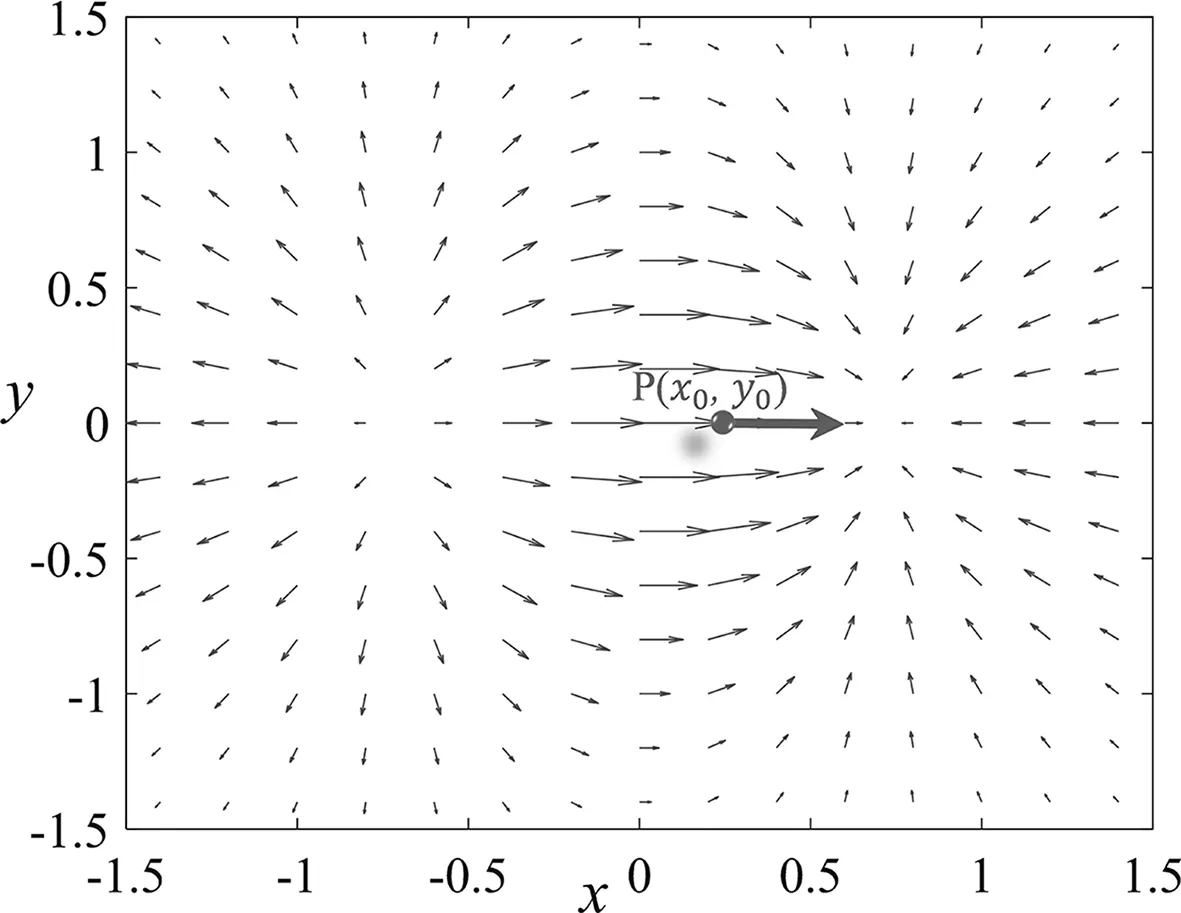
圖3 標(biāo)量場及其梯度的二維投影

四、散度模型

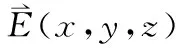
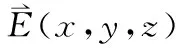
(3)

若梯度研究一個標(biāo)量場在空間某一點的變化,散度則研究一個具有不同極化方向的矢量場在空間某一點的變化,但矢量場的每一個分量實則為一個標(biāo)量場。比如,Ex(x,y,z)、Ey(x,y,z)和Ez(x,y,z)均是標(biāo)量場。這里的物理概念學(xué)生容易混淆,容易把場量的下角標(biāo)表示的極化方向和括號里表示空間分布的自變量發(fā)生混淆。這是一個教學(xué)重點和難點,需要結(jié)合物理模型進(jìn)行闡釋、強(qiáng)調(diào)和區(qū)分。

(4)

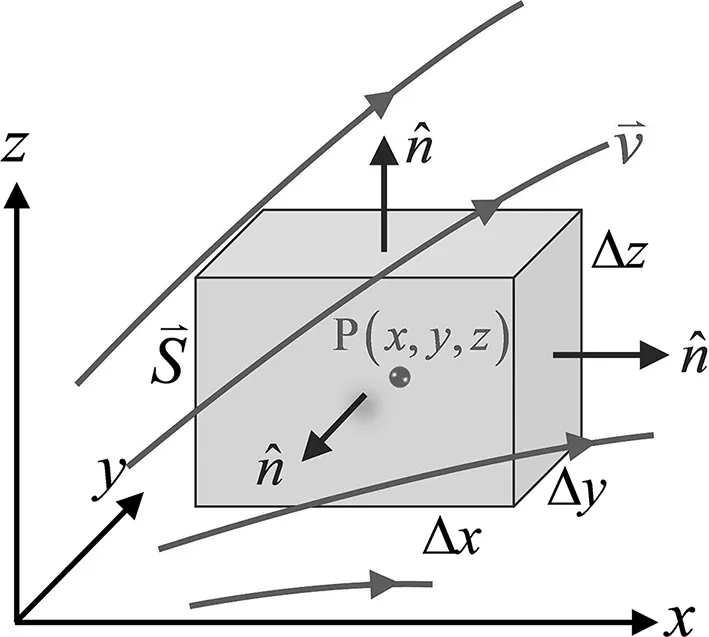
圖4 研究散度的流速場模型

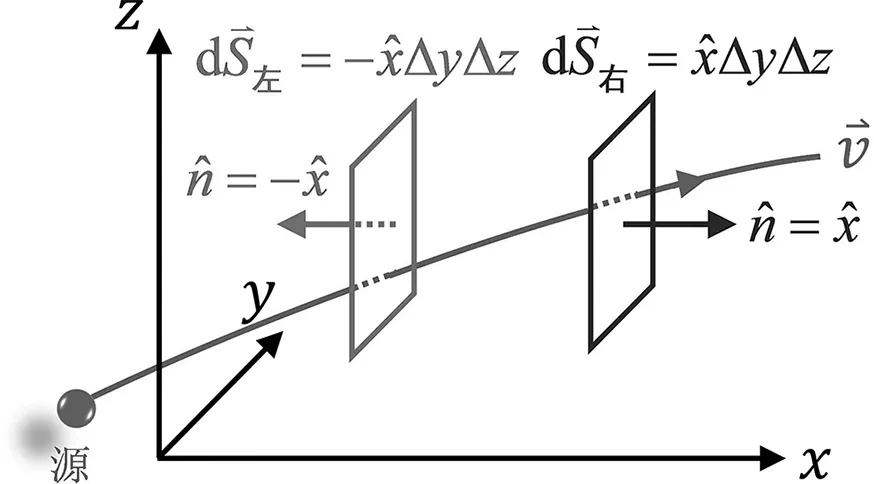
圖5 流速場的源在封閉曲面外部

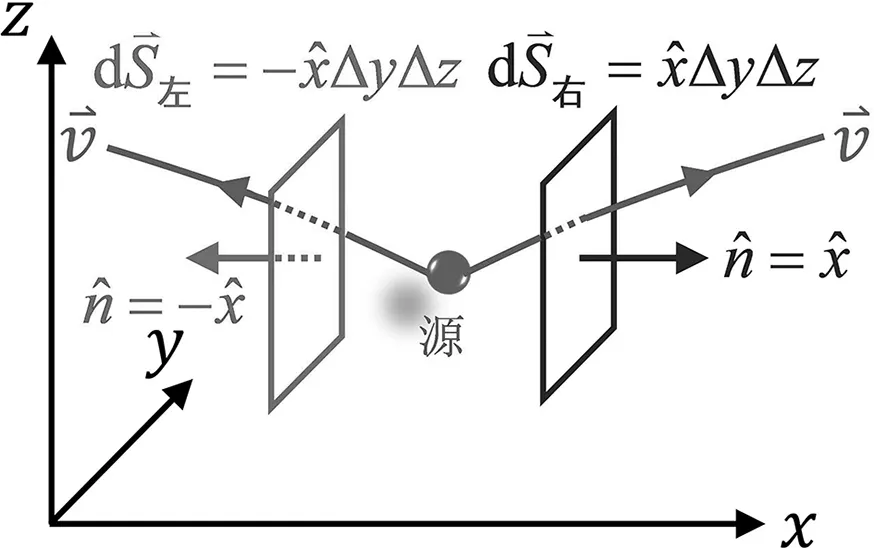
圖6 流速場的源在封閉曲面內(nèi)部

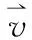
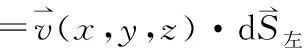
=-vx(x,y,z)ΔyΔz

(5)

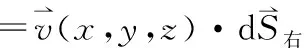
=vx(x,y,z)ΔyΔz

(6)

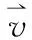
ψ總=ψ左+ψ右+ψ前+ψ后+ψ下+ψ上

=-vx(x,y,z)ΔyΔz+vx(x,y,z)ΔyΔz

-vy(x,y,z)ΔxΔz+vy(x,y,z)ΔxΔz

-vz(x,y,z)ΔxΔy+vz(x,y,z)ΔxΔy

=0

(7)

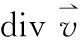
(8)

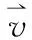
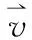
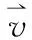
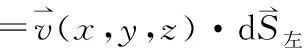
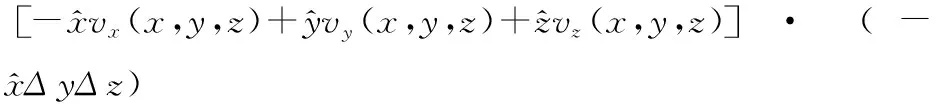
=vx(x,y,z)ΔyΔz

(9)

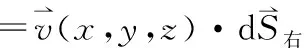
=vx(x,y,z)ΔyΔz

(10)

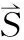
同理,可用同樣的方法求出其他四個面上的通量:

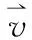
(11)

通過研究通量或散度來了解其通量源的特性,可避免直接研究通量源。利用橫截面上截獲的通量獲取截面內(nèi)場源的大小是一種研究矢量場源的方式。

五、旋度模型

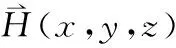
電磁場理論中,一個矢量場的旋度一直是一個教學(xué)難點。為便于學(xué)生理解,在此用一個簡單的旋度計模型來闡釋其原理,如圖7所示。

圖7中不導(dǎo)電圓盤在xoy平面上。圓盤上沿x軸和y軸方向用兩根不導(dǎo)電細(xì)棍固定四個帶相同正電荷量的小球A、B、C和D,這個沿xoy平面的結(jié)構(gòu)可自由轉(zhuǎn)動。它通過一段彈力線與沿z軸放置的一根不導(dǎo)電圓柱相連。該圓柱固定不動。四個小球受到電場力E左、E右、E前和E后的作用,如圖8所示。

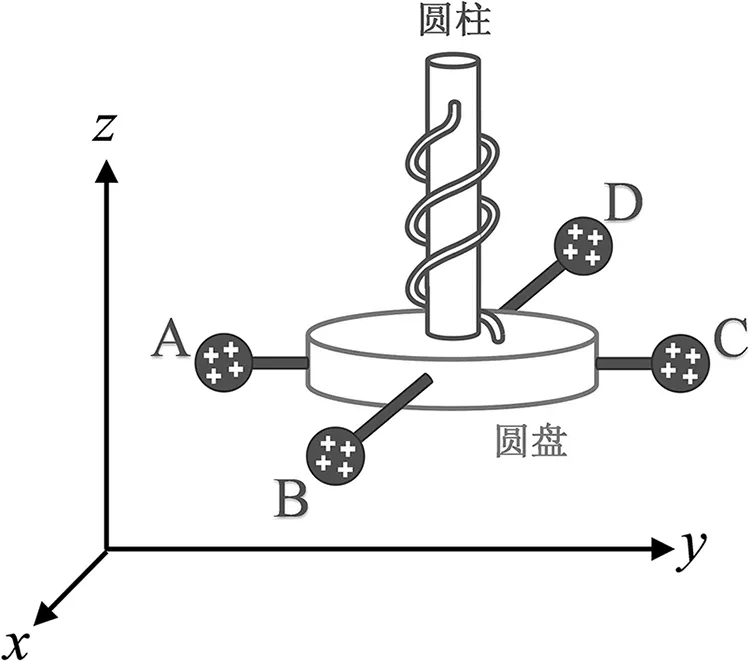
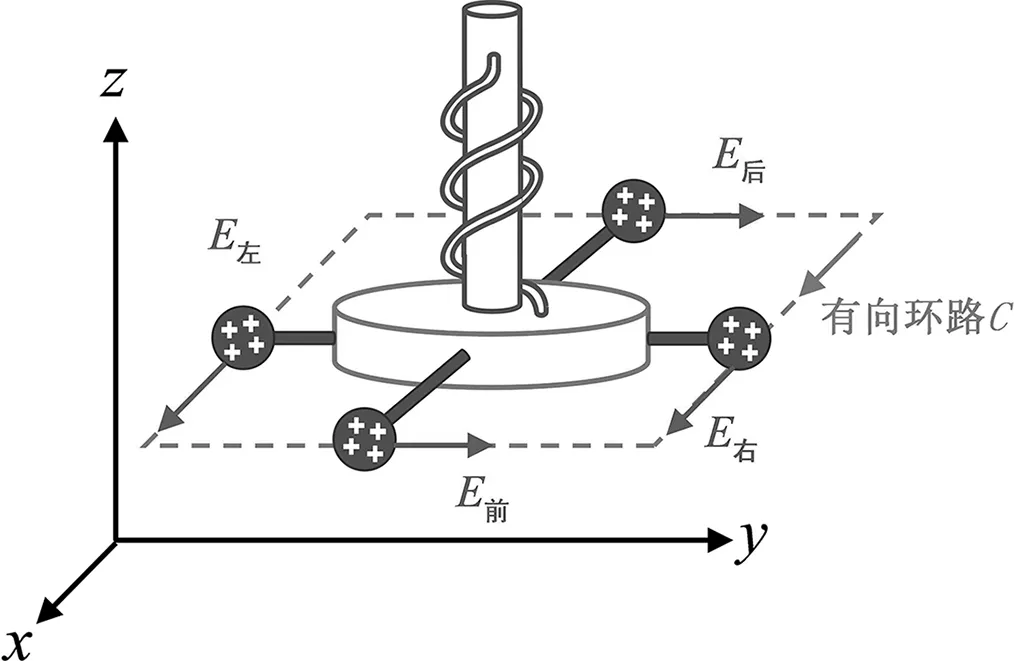
圖7 旋度計模型圖 圖8 帶電小球所受電場力

其中,有向環(huán)路C的方向為順時針方向。電場力E左和E右沿x軸方向,E前和E后沿y軸方向,在此研究沿一個方向的兩個電場力的效果足以說明問題。

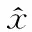
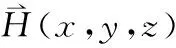
(12)

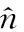
(13)

(14)

(15)

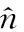
(16)

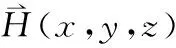
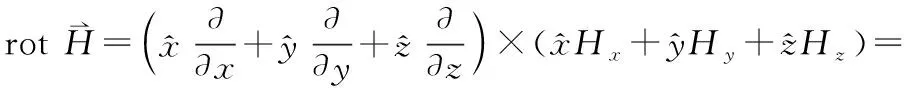
(17)

更多具體表示式可參見教材[2],在此,可利用“旋度計”模型深入理解旋度的概念。

結(jié)語

本論文針對教學(xué)中的重點和難點——哈密頓算子、梯度、散度和旋度,利用圖形和模型進(jìn)行詳細(xì)闡釋。講解哈密頓算子的時候,首先讓學(xué)生回顧時間軸上導(dǎo)函數(shù)的定義,再過渡到空間上的導(dǎo)函數(shù)。講解標(biāo)量場的梯度時,利用二維坐標(biāo)系和三維坐標(biāo)系視角進(jìn)行詮釋。講解散度時,利用流速場模型進(jìn)行類比。講解旋度時,利用“旋度計”模型輔助學(xué)生理解。與此同時,還詮釋了空間矢量場的下角標(biāo)和自變量的物理意義。教學(xué)實踐表明,本文對“電磁場與電磁波”系列課程中這部分內(nèi)容的授課很有幫助。