基于多模型融合的鋰離子電池SOC自適應估計

吳逸洲，劉 艷，祝現染，王譯萱

(1.華東光電集成器件研究所，江蘇蘇州 215000；2.北京理工大學，北京 100089)

鋰離子電池是目前電動汽車行業廣泛采用的儲能元件。電動汽車的電池荷電狀態(SOC)相當于燃油車的油量，可用于實時監控電池狀態，避免車輛在行駛過程中的故障發生。由于無法對電池的SOC進行直接測量，研究者通常采用參數估計的方法確定SOC。電池在實際使用過程中的環境復雜，受到溫度、阻抗和放電倍率等多種因素的影響，涉及參數繁多，使SOC準確估計的難度較高。

基于鋰離子電池的容量衰減分布規律，建立電池容量衰減模型，能夠提升參數數據較少時的電池容量預測能力。在電池容量預測的相關研究中，國內外學者就電池容量衰減模型開展了一系列試驗研究。例如，黎火林等[1]對不同溫度和放電倍率開展了電池壽命加速試驗，表明隨著電池充放電循環次數的增加，電池容量分布符合冪函數規律。Liaw 等[2]從溫度和SOC的參數出發，對電池加速壽命試驗進行設計，發現與溫度相關的阻抗、功率和額定容量的變化符合Arrhenius公式。Atalay 等[3]根據P2D 模型，開發了一種基于SEI 膜生長和負極析鋰的壽命衰降模型，該模型能夠對電池的循環壽命衰降和壽命末期的跳水現象進行準確預測。綜上，在國內外有關電池容量衰減模型的研究中，大多基于恒定條件下的電池加速壽命試驗數據，對電池容量衰減進行擬合，但在實際的電池應用中，預測精度會隨著電池的老化逐漸降低。因此，迫切需要考慮電池老化現象，對電池容量衰減進行更加準確的估計。

電池循環和存儲過程中的衰降是鋰離子電池容量衰減的主要來源[4]。為對鋰離子電池循環導致的衰減進行模型搭建，本文采用FFRLS 算法進行模型參數的在線辨識，并形成了動力電池SOC的估計方法。結合電池加速老化試驗數據，建立了動態應力下的電池容量衰減模型，更加準確地對電池SOC進行預測。最后，采用自適應卡爾曼濾波算法，建立了自適應SOC估計模型，以提高該模型對不精確SOC初值的修正能力。

1 電池試驗

本文采用錳酸鋰電池單體作為試驗對象，該電池額定容量為45 Ah，充放電截止電壓為3.0～4.2 V。試驗設備為FTF2-500/50-750 型動力電池測試系統和EWER-A3-40-CP-AR 型步入式環境艙。通過必測系統上位機編輯了靜態容量試驗、混合脈沖特性和開路電壓試驗。

2 電池模型

2.1 等效電路模型

He 等[5]發現，DP 等效電路模型對電池的預測精度性能最佳，其動態電壓特性可等效為圖1 所示，包括開路電壓Uoc、2條RC 網絡和電阻R0。圖中：R0模擬電壓突變的電阻特性；Rd、Cd分別表征由濃差極化的電阻和電容；Rc、Cc表征由電化學極化的電阻和電容。

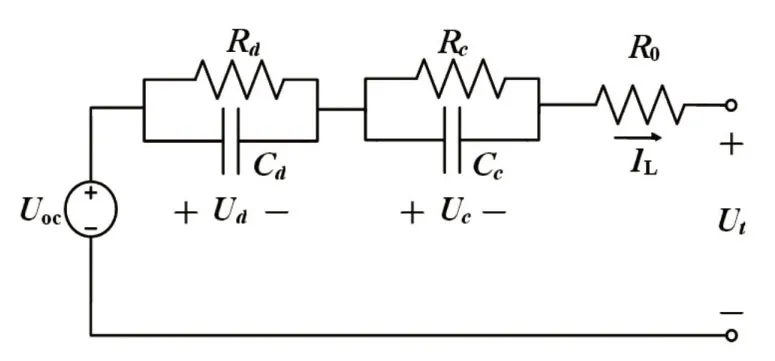
圖1 等效電路模型

該模型的狀態方程如下：

式中：Ut為電池電壓；Ud、Uc分別為Rd、Rc電壓；IL為充放電流。

2.2 在線參數辨識

采用遺忘因子遞推最小二乘法(FFRLS)實現參數在線辨識，可有效解決因參數變化慢導致的參數估計不準的問題[6]。為避免遞推發生“數據飽和”，本文設置遺忘因子l，具體算法流程如圖2 所示。

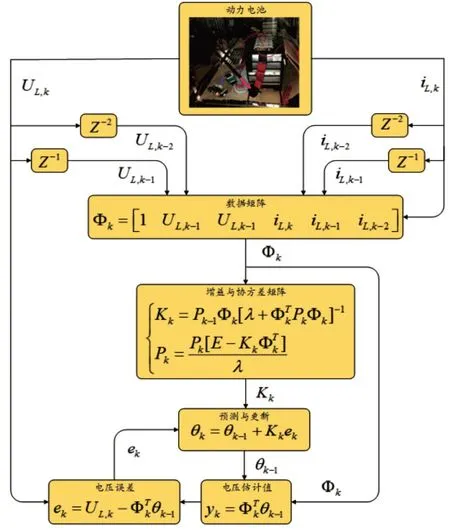
圖2 基于FFRLS方法的電池模型參數在線辨識流程

電池模型轉化如下：

式中：ek為零均值白噪聲；θk為參數矩陣；Φk為數據矩陣。

對式(1)進行拉普拉斯變換：

采用歐拉法將上式離散化，變換公式為：

其中T為采樣間隔時間，代入式(4)中，可得到：

對式(5)進行z反變換，得到差分方程：

由于采樣時間T較小，在T時間內開路電壓Uoc基本無變化，故：

式(6)可簡化為：

得到電池模型輸出矩陣yk、參數矩陣θ和數據矩陣Φ：

2.3 電池容量衰減模型

2.3.1 恒定應力下的電池容量衰減模型

電池每次循環充放電都會造成微小的容量損失ΔC，經t次循環，電池累積容量衰減量為x(s,t)。由中心極限定理可知，當t足夠大時，x(s,t)近似正態分布[7]，即電池容量的衰減過程為高斯過程。因此電池在應力s下的容量衰減服從如下正態分布：

式中：u(s,t)和σ2(t)分別為在應力水平s下，電池循環t次后的容量衰減量均值和容量衰減量方差。

從統計學的角度考慮，應按照加速老化試驗的數據，對動力電池的容量衰減量進行最大似然估計，并取容量衰減量均值u(s,t)的估計值作為預測模型的特征值。將u(s,t)進行曲線擬合與回歸分析，得到電池的容量衰減方程式：

式中：s為應力類型；hi(s)為常數。當應力s分別選擇溫度T和放電倍率Rd時，i=1,2。

本文以恒定小倍率電流充電，故不考慮充電倍率的影響。

2.3.1.1 基于溫度應力的容量衰減模型

參考Matthieu 等[8]提出的阿倫尼烏斯模型，列出衰減方程系數：

式中：k、F為與應力及時間無關的常數；T為絕對溫度。

令G=lnk，則：

由式(11)，得到容量衰減模型：

將上式數據進行擬合，得到參數G、F和h1(T)的值。

在20 和40 ℃下，電池容量的衰減情況如表1 所示，電池循環300 次的容量衰減擬合結果見圖3。

表1 不同溫度下的電池容量衰減情況(0.5 C 充電，1 C 放電)

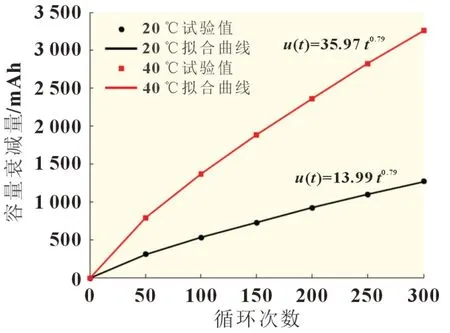
圖3 20和40 ℃下的電池容量衰減擬合曲線

根據式(14)和圖3 的擬合結果，得到如下公式：

對上述方程進行求解，得到F=-433 0.2，G=17.4，則電池在溫度應力下的衰減方程為：

2.3.1.2 基于放電倍率應力的容量衰減模型

在加速壽命試驗中，作為加速的電應力一般服從逆冪律關系[9]：

式中：ξ為壽命特征值；A為正常數；ν為電應力；c為與激活能有關的正常數。

由容量衰減方程式(11)，可得到動力電池的平均壽命L：

式中：l為失效閾值，即實際容量衰減為初始值的80%。

當ξ作為電池壽命的平均值時，D=為正常數，c=chi(ν)是與激活能相關的正常數。將放電倍率設為加速應力，代入上述公式進行推導，得到Rd的容量衰減模型為：

式中：D、c、E和h2(Rd)均為常數。

根據電池加速壽命試驗，得到循環300 次的電池容量衰減情況，如表2 所示。根據表2 的數據，得到圖4 所示的1C、2C和3C下的循環次數與電池容量衰減擬合曲線，衰減方程參數如表3 所示。

表2 1 C、2 C 和3 C 下的電池容量衰減情況

表3 1 C、2 C 和3 C 下的電池容量衰減方程參數

圖4 1 C、2 C和3 C下的電池容量衰減擬合圖

令h2(Rd)≈0.79。對衰減參數進行擬合，得到電池容量衰減方程系數曲線，如圖5 所示，其表達式為：

圖5 不同放電倍率的容量衰減參數曲線

根據式(19)，得到電池模組在不同放電倍率下的衰減方程，即：

2.3.1.3 復合應力下的容量衰減模型

在上述模型中增加溫度應力的加速衰減因子，本文建立了復合應力下的容量衰減模型。溫度應力的Ⅱ型加速衰減因子與時刻t無關[10]，即：

將式(22)中的溫度分別取T1=T0、T2=T，則可得到在(T,Rd)應力條件下的電池容量衰減模型，即：

則式(23)可寫成：

根據式(16)和式(22)，可得到容量加速衰減因子，即：

根據式(21)和式(26)，可得到在(T,Rd)應力條件下電池容量的衰減模型，即：

2.3.2 動態應力下的電池容量衰減模型

上述三種電池容量衰減模型是通過300 次電池循環數據擬合所得，因數據量較少，其預測性能隨電池的老化而變差。由于車輛行駛過程中的動力電池并非以恒流工作，而是按功率放電，因此，當電池容量衰減時，內阻也隨之增大，導致電壓平臺變低。為滿足同功率輸出，需提高放電電流，即放電倍率伴隨容量衰減有增大趨勢。由此，本文建立了動態應力下的電池容量衰減模型，以提高電池容量衰減預測的精確性[11]。

由于動力電池的容量衰減呈非線性，電池每輪衰減度受到單次循環最大有效容量的影響。基于實時電池容量狀態的動態應力，本文構建了容量衰減模型。記ut(T,Rd)為t次循環時的容量衰減量，ut+1(T,Rd)為t+1 次循環時的容量衰減量，則有：

式中：ut+1(T,Rd)為t輪循環后的電池容量衰減量，表示在(T,Rd)的作用下，第t+1 輪循環后的衰減總量；ut(T,Rd)為t輪循環后的電池容量衰減總量，與t－1 輪的衰減量及應力水平相關。

記Ti、Rd,i分別為第i輪循環時的應力，則公式(28)可以轉化為：

進一步可以得到經過m輪循環后的衰減量ut+m(Tt+m,Rd,t+m)，即：

根據本研究開展的加速壽命試驗的電池擬合系數，得到電池容量衰減系數方程：

由容量衰減模型公式(30)和衰減系數方程(31)，推導出第t－1 輪循環后的最大有效容量Ct的預測模型如下：

Ti、Rd,i的取值方式如下：由于溫度變化相對較慢，設定電池溫度采集頻率為0.01 Hz，Ti為i輪循環中采集溫度的平均值；由于放電倍率并非恒定，設定放電電流采集頻率為1 Hz，將i輪循環中放電電流平均值與額定容量的比設定為Rd,i。

3 基于多模型融合的自適應SOC 估計

本文采用自適應卡爾曼濾波算法(AEKF)，對模型參數及噪聲統計特性進行修正，以提高SOC的預測精度[12]，使之具有更好的環境適應性。計算流程如下：

首先，對動力電池充電狀態SOC進行離散化，可轉換為：

式中：z為電池充電狀態；η為電池庫侖效率；Δt為采樣時間；C為電池最大有效容量。

其次，對動力電池等效電路模進行離散化處理，得：

由公式(33)和公式(34)，可得到該離散系統中的狀態轉移矩陣與測量矩陣：

根據上述方程，建立動力電池系統狀態方程和觀測方程：

式中：x=[z Ud Uc]T。

最后，通過結合電池模型參數FFRLS 算法、電池容量衰減模型及自適應卡爾曼濾波算法，建立基于多模型融合的自適應SOC估計算法，具體計算流程如圖6 所示。

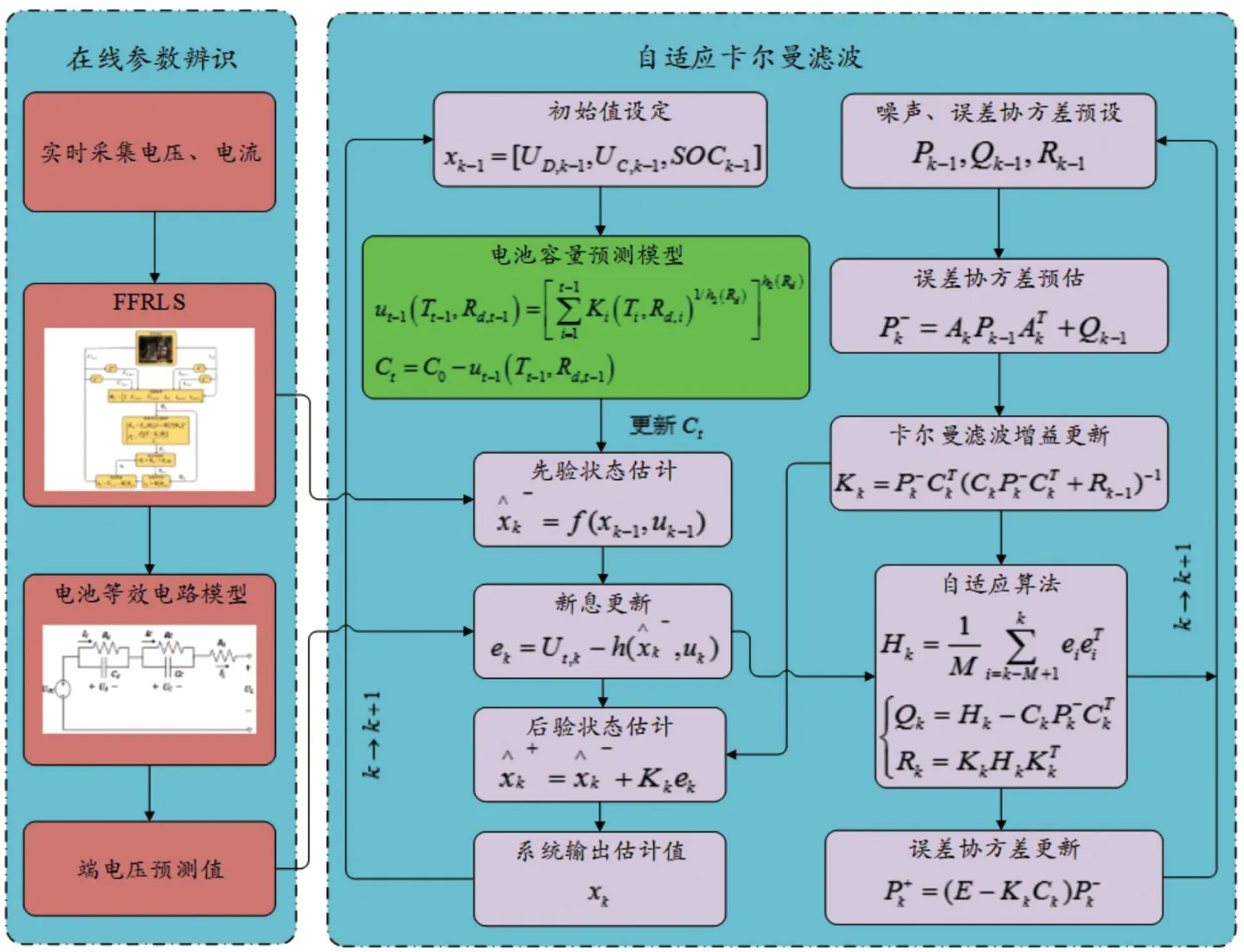
圖6 SOC估算流程

4 SOC 估計算法的仿真與評估

在25 ℃下，電池以城市道路循環(UDDS)工況在90%～20%的SOC區間進行循環充放，每循環5 次進行一次定容，共循環600 次，以第600 次循環數據進行仿真分析。圖7(a)為電池實際容量衰減曲線和預測容量衰減曲線，圖7(b)表明本文所提出的電池容量衰減模型能夠較準確地預測電池容量的衰減過程，預測誤差小于1.5%。

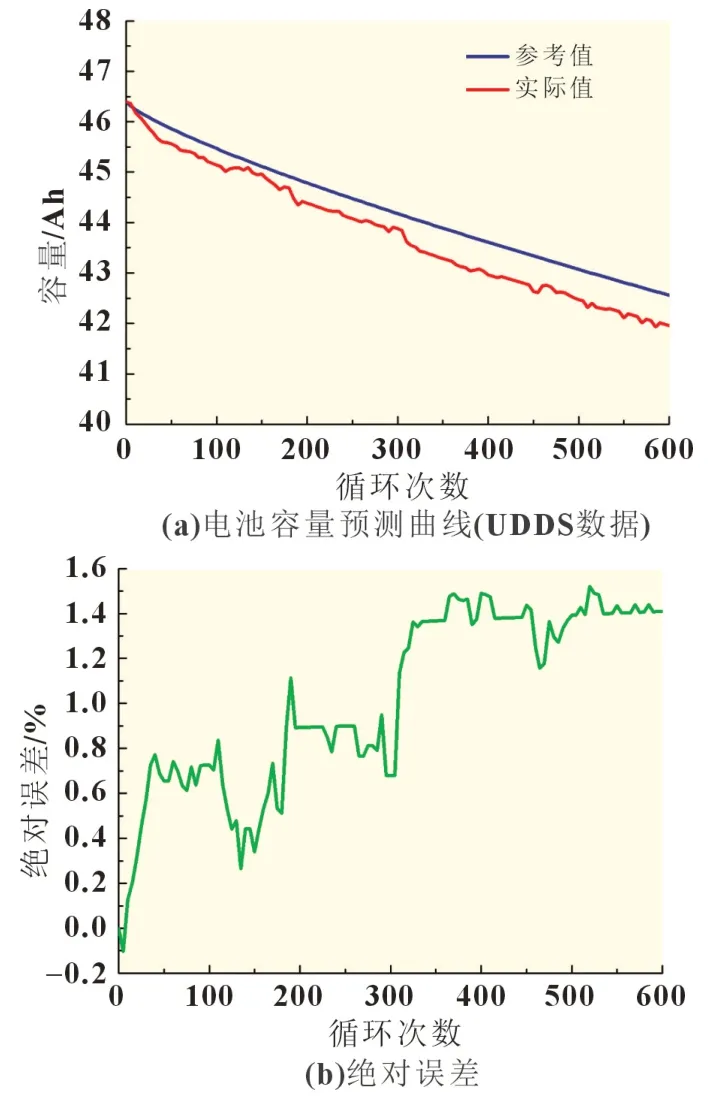
圖7 工況循環下電池實際容量衰減與模型預測對比

圖8(a)是電池第600 次循環中實際SOC參考值曲線和模型估計SOC曲線，可以看出，電池容量更新后的SOC估計曲線與參考值曲線基本吻合。圖8(b)結果顯示，初始SOC誤差在10%的情況下，SOC估計能迅速收斂至真值附近，且能保持SOC估計誤差在1.5%以內。以上結果表明，本文提出的基于電池容量模型的SOC自適應估計算法，在電池容量的預測方面具有很好的魯棒性和較高的估計精度。

圖8 600次循環電池實際SOC曲線與模型估計對比

5 結論

基于鋰離子電池容量衰減的分布規律，本文首先建立了電池等效電路模型，并采用FFRLS 算法對模型參數進行在線辨識，以提高模型預測電壓的精度。然后基于加速壽命試驗數據，建立了恒定應力下的電池容量衰減模型，考慮到電池使用狀態的不穩定性，為了更好地模擬電池容量的實際衰減過程，基于當前電池的容量狀態，建立了動態應力下的電池容量衰減模型。最后根據電池等效電路模型、電池容量衰減模型和自適應卡爾曼濾波算法，提出了基于電池容量模型的自適應SOC估計方法，更好地實現電池SOC的精確估計。經過仿真分析與評估，表明本文所提出的方法能夠實現電池容量和SOC的較準確估計，該算法具有很好的魯棒性和可靠性。