均勻流作用下懸索橋單側并置雙主纜振動特性分析

張太科, 陳上有, 劉 高, 楊佐磊

(1. 廣東省公路建設有限公司,廣州 510100; 2. 廣東灣區交通建設投資有限公司,廣州 510100;3. 中交公路長大橋建設國家工程研究中心有限公司,北京 100088)

懸索橋是大跨度橋梁的主要橋型之一[1],早期已建成懸索橋大都采用雙主纜纜索系統,只有極少數采用單側并置雙主纜的四主纜纜索系統,如美國華盛頓大橋,主跨1 067 m;另外一座是美國維拉扎諾大橋,主跨為1 298 m[2]。隨著橋梁跨度的增加,通行車道的增多,采用雙主纜懸索橋方案,主纜直徑越來越大,主纜的制造、架設和安裝將面臨挑戰。采用四主纜纜索系統可以大幅減小主纜直徑,因此,對于超大跨橋梁,采用單側并置雙主纜的四主纜懸索橋將是一種比較好的選擇。我國的燕磯長江大橋,主跨1 860 m,由于航空限高,采用了不同矢跨比的四主纜懸索橋,將成為我國首座四主纜懸索橋[3]。獅子洋大橋跨度達2 180 m,通行16車道,在初步設計階段也提出了單側并置雙主纜的四主纜懸索橋比選方案[4]。

抗風問題是大跨度懸索橋面臨的主要問題之一[5],對于單側單主纜的雙主纜懸索橋,主纜的風致振動問題主要是馳振。馳振是一種在風作用下由于結構運動產生負阻尼并導致振動發散的空氣動力失穩現象。李勝利等[6-9]對大跨徑懸索橋施工期暫態主纜的馳振系數及馳振臨界風速進行了研究,指出在大跨徑懸索橋主纜的架設過程中有發生馳振失穩的可能性,須采取控制措施。李永樂等[10]基于實橋三維馳振模型,采用時域法分析了主纜馳振性能,結果表明,主纜馳振以反對稱振動為主,隨著風速的增大,馳振卓越頻率逐漸減小,馳振形態由高階模態振動逐步轉變為低階模態振動,當風速較高時,馳振振幅較大,頻率較單一,通常以結構豎向基階模態為主,此時橫橋向振幅較小,振動頻率更低,多模態參振現象明顯。

對于并置雙主纜而言,迎風側主纜對背風側主纜存在氣動干擾,即迎風側主纜在氣動力作用下發生運動,進一步影響自身的氣動力以及下游側主纜的氣動力,進而影響到自身和下游側主纜的運動特性。由于四主纜懸索橋建設經驗比較有限,相關研究較少。早期學者大多針對剛性或彈性支撐的剛體二維模型進行試驗研究或CFD(computational fluid dynamics)模擬。如Dielen等[11]通過彈簧懸掛模型風洞試驗,研究了兩圓柱間距比W/D0≤4(W為兩圓柱中心距,D0為圓柱直徑)時的氣動干擾,發現尾流馳振的臨界風速隨Scruton數和間距比的增大而升高,且當下游圓柱發生尾流馳振時上游圓柱也會出現小幅振動。Tokoro等[12]針對不同間距串列拉索模型進行了剛性支撐風洞試驗,在間距為4.3D,風攻角為15°時觀測到了以一階模態為主的尾流馳振。Sumner等[13]通過風洞試驗測量了兩個等徑交錯圓柱體在橫流中的平均空氣動力和渦流脫落頻率。而實際中橋梁主纜為垂度效應明顯的細長結構,有必要進行考慮垂度的氣彈模型試驗,來研究其三維狀態下的相互干擾特性。Loredo-Souza等[14]開展了兩條平行輸電電纜在強風下的氣彈模型試驗,表明隨著兩條電纜間距增大,其阻力的相干性減小,并且隨著風速的增加而減小。Li等[15]開展了平行拉索三維彈性模型風洞試驗,觀察到尾流馳振對攻角很敏感;偏角約為10°～20°的拉索最容易受到尾流馳振影響;當間距增加時,尾流馳振變得不那么敏感;在多個位置使用剛性連接可以抑制尾流馳振。陳政清等[16]以廣東佛山平勝大橋中的無吊索兩平行主纜為研究背景,在串列主纜模型試驗中觀測到了以一階模態為主的尾流馳振現象,發現主纜間距風偏角及風攻角的變化對尾流馳振臨界風速存在明顯影響。

綜上,單主纜馳振研究主要集中施工期暫態主纜,主要關注馳振臨界風速及控制措施;并置雙主纜風致振動研究較少,主要采用風洞模型試驗手段進分析。本文建立均勻流作用下考慮主纜三維效應、主纜間氣動干擾效應和雙向流固耦合效應的四主纜懸索橋單側并置雙主纜振動分析方法,以廣州獅子洋大橋初步設計階段提出的單跨吊四主纜懸索橋方案為研究背景,對均勻來流作用下成橋狀態中跨主纜的橫向振動,以及邊跨主纜的橫向、豎向振動進行數值模擬,對振動特性進行了分析。

1 均勻流作用下并置雙主纜振動分析方法

1.1 主纜系統運動方程

風荷載作用下橋梁結構的運動方程可表示為

(1)

式中: [M],[C]和[K]為橋梁的質量、阻尼和剛度矩陣;X為橋梁的位移向量;F為橋梁的風荷載向量。

將橋梁整體分解為兩個子系統,即主纜子系統和除主纜之外的子系統,橋梁整體運動方程式(1)改寫為

(2)

式中: 下標ca和ot分別為主纜子系統和除主纜之外的子系統;下標co或者oc為主纜子系統和除主纜之外的子系統之間相互影響部分。

采用振型分解法,當重點關注主纜的運動時,選擇主纜的前幾階主振型來近似表達系統的位移向量。為簡化推導,這里暫且以單階振型來表達系統位移,此時橋梁運動方程可以表示為

X=φiqi

(3)

(4)

式中:φi為關于主纜的i階主振型;qi,ωi和ξi分別為主纜i階主振型對應的模態坐標、振動頻率和阻尼比。

振型向量也分解為主纜子系統和其他子系統兩部分,即

(5)

當選擇以主纜為主的振型時,φi,ot相對于φi,ca部分而言可以忽略不計。由于一般情況下主纜的縱向、橫向和豎向振型是相互獨立的,且橫風作用下縱向振動不容易發生,因此如下所示。

(1) 當φi是以主纜橫向振動為主的振型時

(6)

式中:φcaH,i和FcaH為主纜橫向振動自由度對應的振型和風荷載;qHi,ωHi和ξHi分別為主纜橫向振動的模態坐標、振動頻率和阻尼比。

(2) 當φi是以主纜豎向振動為主的振型時

(7)

式中:φcaV,i和FcaV為主纜豎向振動自由度對應的振型和風荷載;qVi,ωVi和ξVi分別為主纜豎向振動的模態坐標、振動頻率和阻尼比。

1.2 主纜風荷載簡化

由于主纜是三維結構,不同高度處主纜單位長度上的風荷載是不同的。為簡化計算,假設不同高度處的阻力系數是相同的,則單根主纜節點j上的橫向風荷載可表示為

(8)

其中

(9)

(10)

式中:zj為節點j的高程;α為風剖面指數;Lj為節點j對應的長度;D為主纜截面直徑;U0,z0,CD0(t)和H0(t)分別為參考點0處的風速、高程、主纜斷面阻力系數和主纜單位長度的風阻力;Cj為節點j相對于參考點0的風阻力調整系數。

主纜橫向風荷載FcaH可以表示為

FcaH={H1(t)H2(t) …Hn(t)}T=
H0(t){C1C2…Cn}T=CH0(t)

(11)

與主纜橫向風荷載簡化過程類似,主纜豎向風荷載FcaV可以表示為

FcaV={V1(t)V2(t) …Vn(t)}T=
V0(t){C1C2…Cn}T=CV0(t)

(12)

其中

(13)

式中,CL0(t)和V0(t)分別為參考點0處的主纜斷面升力系數和主纜單位長度風升力。

上述推導過程中,假設不同高度處的阻力系數是相同的,將整根三維主纜的風荷載用參考點處主纜單位長度風荷載進行表達,從而可用二維CFD模型進行求解,因此,這種處理方式相當于是將難以處理的三維問題轉化為二維問題,從而降低了計算難度。當然,不同高度處的阻力系數可能并不完全相同,上述處理方式存在一定誤差,如要提高計算精度,可以將主纜分為多個區段,每個區段內選擇代表性參考點,每個區段的主纜風荷載用區段內代表性參考點處主纜單位長度風荷載表達。雖然這樣處理可以提高精度,但是也大大增加了計算的工作量。

1.3 單側并置雙主纜簡化運動方程

根據1.1節和1.2節,主纜橫向和豎向振動一階近似可以表示為

(14)

(15)

其中

(16)

(17)

以迎風側主纜為例,在計算得到了迎風側主纜參考位置處的主纜單位長度風升力H0f或風阻力V0f后,迎風側主纜的模態坐標可以通過式(14)～式(17)求得,進而求得迎風側主纜任意位置的位移,如參考點處的位移可表示為

xH0f=φcaH,i-0fqHif

(18)

xV0f=φcaV,i-0fqVif

(19)

式中:φcaH,i-0f和φcaV,i-0f分別為迎風側主纜參考點處的第i階振型的橫向分量和豎向分量;qHif和qVif分別為迎風側主纜的第i階振型模態坐標。

同理,可以求得背風側主纜的模態坐標qHir和qVir,以及參考點位置處的位移xH0r和xV0r,此處不再贅述。

1.4 多模態振動

為簡化,上述推導過程中只考慮單了一階振型振動即單模態振動,當考慮多個模態振動時,只需聯立多個相互獨立的方程求解各階模態坐標即可,例如迎風側主纜參考點處的位移可表示為

(20)

式中:φHk-0f為迎風側主纜參考點處的第k階振型的橫向分量;qHkf為迎風側主纜第k階振型的模態坐標;N為計算中考慮的模態階數。

2 均勻流作用下并置雙主纜運動求解方法

2.1 并置雙主纜氣動干擾效應

相比單側單主纜而言,并置雙主纜由于迎風主纜和背風主纜氣動干擾,在計算參考點處的單位長度風阻力H0f(t)和H0r(t),以及風升力V0f(t)和V0r(t)時,需要考慮迎風主纜、背風主纜之間的氣動干擾效應。

由于迎風主纜、背風主纜之間的位置隨著時間變化而變化,導致迎風主纜、背風主纜之間的氣動干擾效應是隨時間變化而變化的,因此,為準確地考慮迎風主纜、背風主纜之間的氣動干擾效應,需要建立迎風主纜、背風主纜的雙向流固耦合模型進行求解。

2.2 計算分析流程

整個計算分析流程如圖1所示。分析中最主要的工作是采用CFD方法獲得主纜上的流體作用力和求解結構動力學方程獲得主纜的運動狀態。主要計算步驟包括:

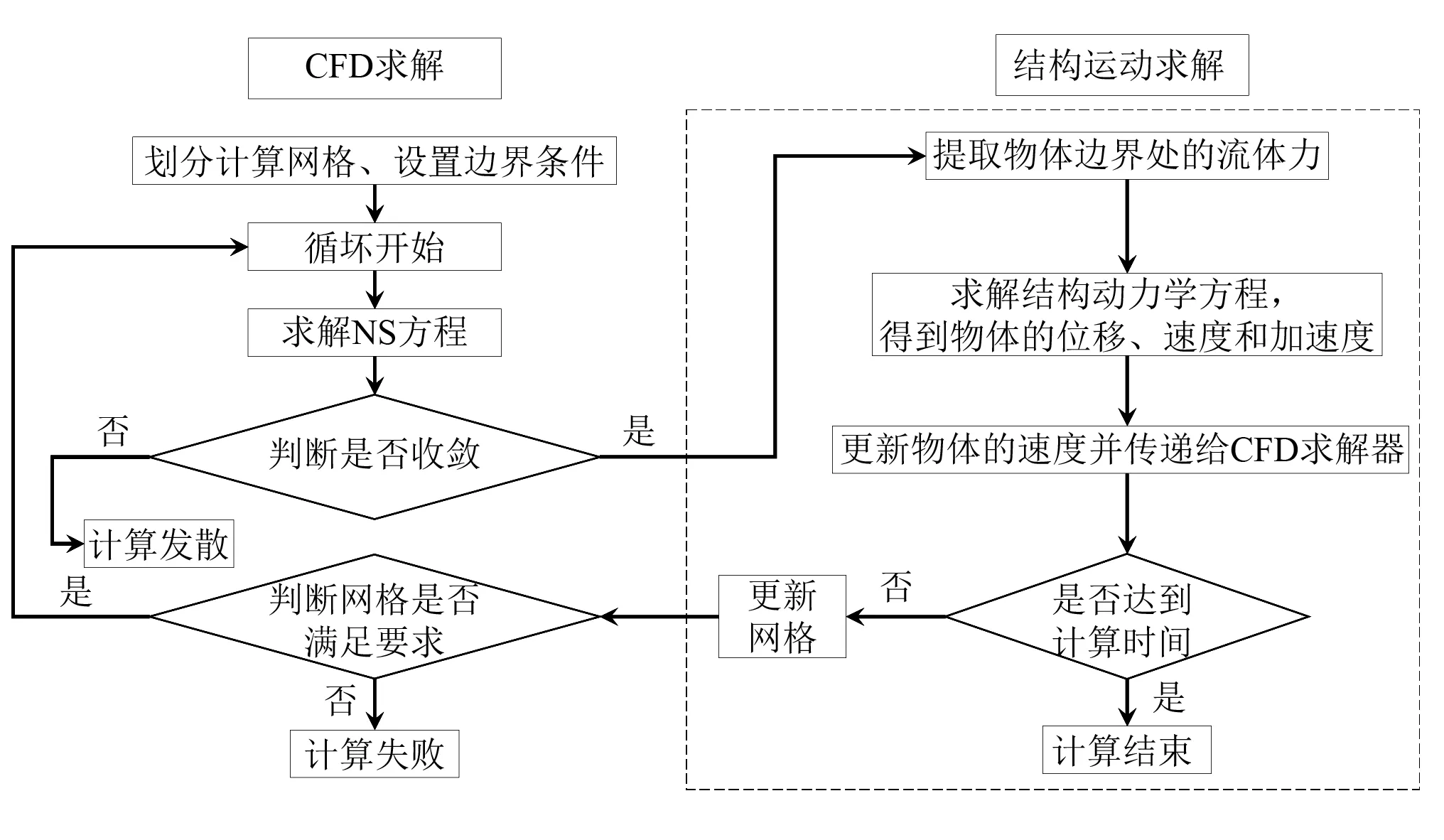
圖1 計算流程Fig.1 Calculation process

步驟1劃分計算域網格,設定邊界類型。

步驟2根據t時刻主纜的位移,更新網格。

步驟3計算t時刻的參考點處主纜單位長度受到的風荷載H0f(t),V0f(t);H0r(t),V0r(t)。

步驟4采用龍格庫塔法求解迎風側主纜和背風側主纜的模態坐標方程,計算t+dt時刻的模態坐標qHif,qVif,qHir和qVir,進而得到t+dt時刻參考點處主纜的運動位移xH0f,xV0f,xH0r和xV0r。

步驟5令t=t+dt,重復步驟2～步驟4,直到計算時間結束。

3 主跨2 000 m懸索橋單側并置雙主纜振動分析

3.1 橋梁方案簡介

獅子洋大橋主跨2 180 m,通行16車道,在初步設計階段,設計院提出了單側并置雙主纜分離式吊索的四主纜單跨吊懸索橋方案,主纜鎖夾外直徑1.0 m,中跨雙主纜設計中心間距3 m,邊跨雙主纜設計中心間距3.0～19.5 m主纜-主梁結構效果圖,如圖2所示。

圖2 主纜-主梁結構效果圖Fig.2 Main cable-main beam structure renderings

成橋狀態中跨主纜受主梁約束,主纜豎向振動與主梁豎向振動耦合,迎風主纜和背風主纜將保持同步振動。由于主梁受風作用帶動迎風側主纜和背風側主纜的運動是相同的,本文主要研究橫風作用下的雙主纜橫向相對運動,因此,只關注迎風側主纜和背風側主纜的自身振動即可。主纜一階橫向振動頻率為0.163 8 Hz,振型如圖3所示。

圖3 中跨主纜橫向一階振型Fig.3 Transverse first-order mode shape of mid-span main cable

成橋狀態邊跨主纜不受主梁約束,主纜振動表現為橫向振動和豎向振動。本文對橫風作用下的主梁橫向振動和豎向振動進行同步模擬。邊跨主纜一階橫向振動頻率0.193 9 Hz,一階豎向振動頻率0.201 5 Hz,相應的一階橫向和豎向振型如圖4和圖5所示。

圖4 邊跨主纜橫向一階振型Fig.4 Transverse first-order mode shape of side span main cable

圖5 邊跨主纜豎向一階振型Fig.5 Vertical first-order mode shape of side span main cable

3.2 成橋狀態中跨主纜

采用RANS 方程和RNGk-ε湍流模型模擬流場,模型計算域及邊界條件示意圖,如圖6所示。主纜直徑D=1.0 m,計算域橫向尺寸為20D,豎向尺寸為10D,兩主纜中心間距為3D,兩主纜間距中點位于計算域的中心位置。入口為速度入口,出口為壓力出口,兩側為對稱邊界,主纜為壁面邊界。

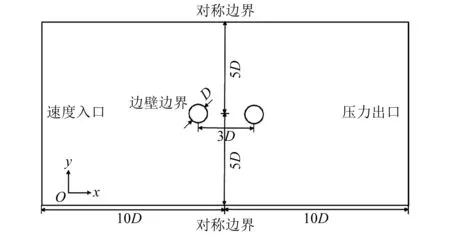
圖6 中跨主纜流固耦合計算域及邊界條件示意圖Fig.6 Schematic diagram of the fluid-structure coupling calculation domain and boundary conditions of the mid-span main cable

針對均勻風速3.5～42.0 m/s(橋址處10 m高10 min平均風速,下同)作用下中跨主纜振動進行模擬。主纜阻尼比假設為5‰。

部分風速下迎風側、背風側主纜風致振動位移響應時程,如圖7所示。從計算結果可以看出:①主纜振動主要表現為簡諧振動;②迎風側、背風側主纜的振動頻率基本相同;③迎風側、背風側主纜的振動幅值不同;④迎風側、背風側主纜振動存在相位差。

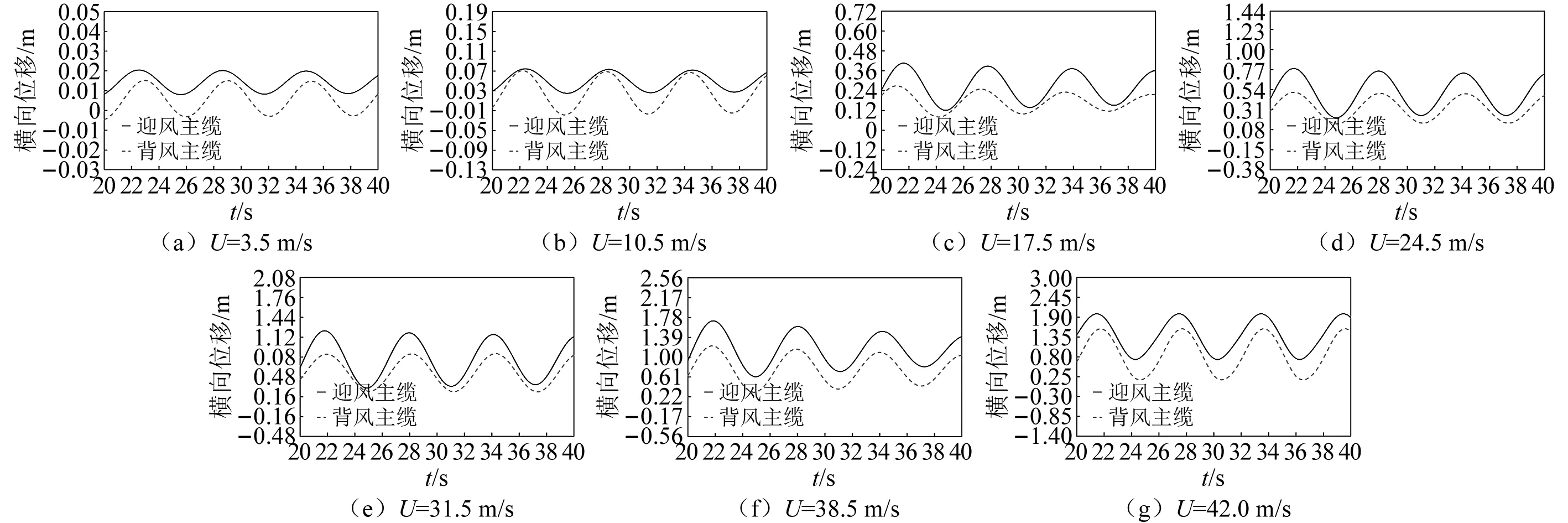
圖7 不同風速下中跨并置雙主纜的振動位移時程Fig.7 Vibration displacement time history of mid-span juxtaposed double main cables under different wind speeds

迎風側、背風側主纜運動幅值隨風速變化情況,如圖8所示。由圖8可知:①迎風側、背風側主纜振動平均值、最大值隨風速增大而增大;②迎風側、背風側主纜的振動幅值隨風速非線性變化,當風速為42.0 m/s時,最大振幅接近0.7 m。

隨著風速增加,迎風側、背風側主纜的中心間距減小,當風速為42.0 m/s時,最小間距為1.9 m,大于并置雙主纜接觸時的最小中心間距1.0 m,表明兩主纜不會發生接觸。

3.3 成橋狀態邊跨主纜

設計方案中邊跨主纜中心距是變化的,本研究中假設主纜按等間距3 m布置,這樣分析結果將是偏安全的。由于邊跨主纜豎向無主梁約束,迎風側、背風側主纜的氣動干擾現象將更加明顯,尾流馳振發生概率大。在CFD模型中,考慮風攻角影響。風攻角α定義為風的主流方向與兩主纜中心連線之間的夾角,其中背風側主纜中心在與迎風側主纜中心連線的下方時,風攻角為正,反之風攻角為負,如圖9所示。對邊跨主纜橫向和豎向振動進行模擬,主纜阻尼比假設為5‰。

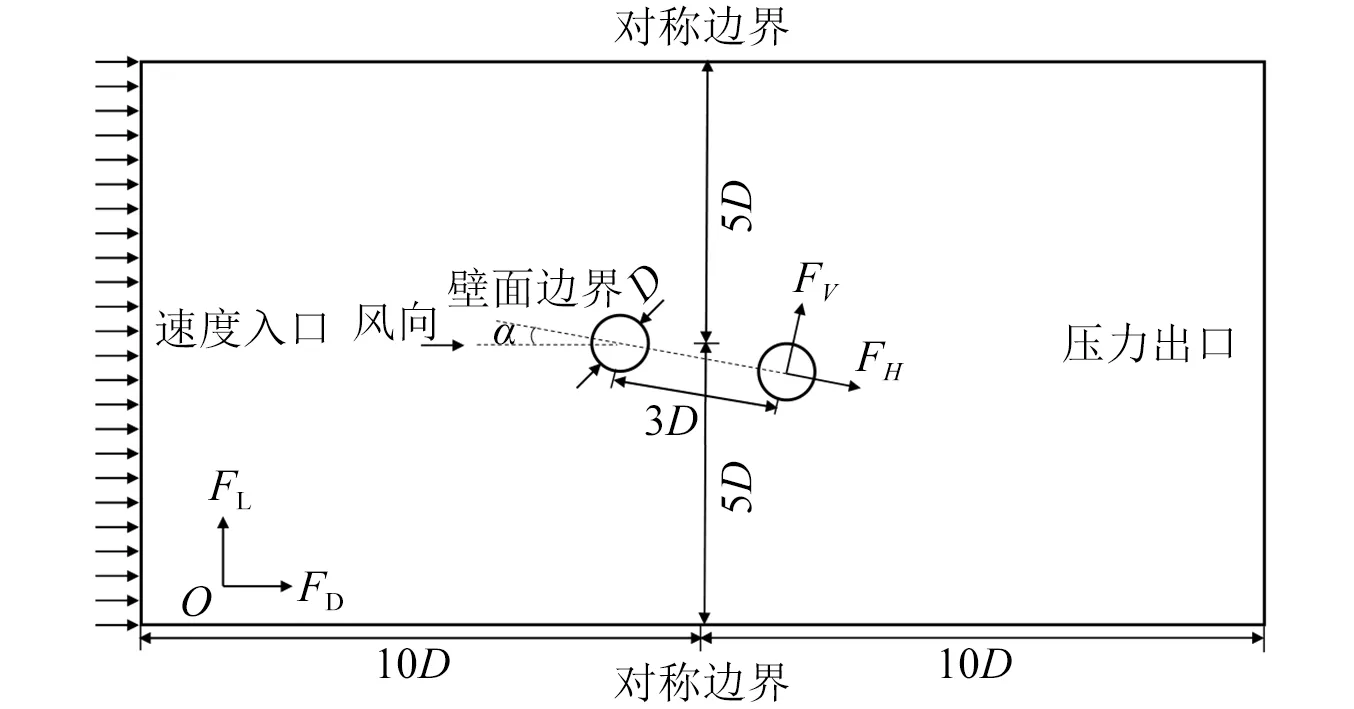
圖9 邊跨主纜流固耦合計算域及邊界條件示意圖Fig.9 Schematic diagram of fluid-structure coupling calculation domain and boundary conditions of side span main cable

對-3°～3°間隔1°共7個風攻角及21 m/s和41.5 m/s兩個風速作用下的邊跨并置雙主纜振動進行模擬。結果顯示,除了風攻角0°工況外,其他工況下的主纜振動無明顯發散現象。針對風攻角0°工況,進一步補充計算了26 m/s,31.5 m/s和38.5 m/s共3個風速工況的振動響應。當風攻角為0°時不同風速作用下的主纜振動時程如圖10所示。主纜振動幅值如圖11所示。風速38.5 m/s工況下不同時刻邊跨雙主纜周圍風速矢量,如圖12所示。由圖10可知:當風速為26 m/s時,背風側主纜豎向位移幅值隨時間周期性變化,表現出類似于“拍”的振動現象,但最大振幅出現在前100 s;當風速為41.5 m/s時,背風側主纜豎向位移幅值隨時間逐漸增大后減小最終趨于穩定;其他風速工況時背風側主纜豎向位移幅值隨時間逐漸增大最終趨于穩定。由圖11可知,隨著風速的增加,主纜振動幅值先逐漸增大,一定風速后幅值有所減小。迎風側主纜豎向位移幅值隨時間變化非常小,隨風速變化的趨勢與背風側主纜相似,但幅值比背風側主纜小得多。從上述結果表明,當風攻角為0°時,邊跨背風側主纜存在尾流馳振現象。

圖11 不同風速下邊跨主纜振動幅值Fig.11 Vibration amplitude of side span main cable under different wind speeds

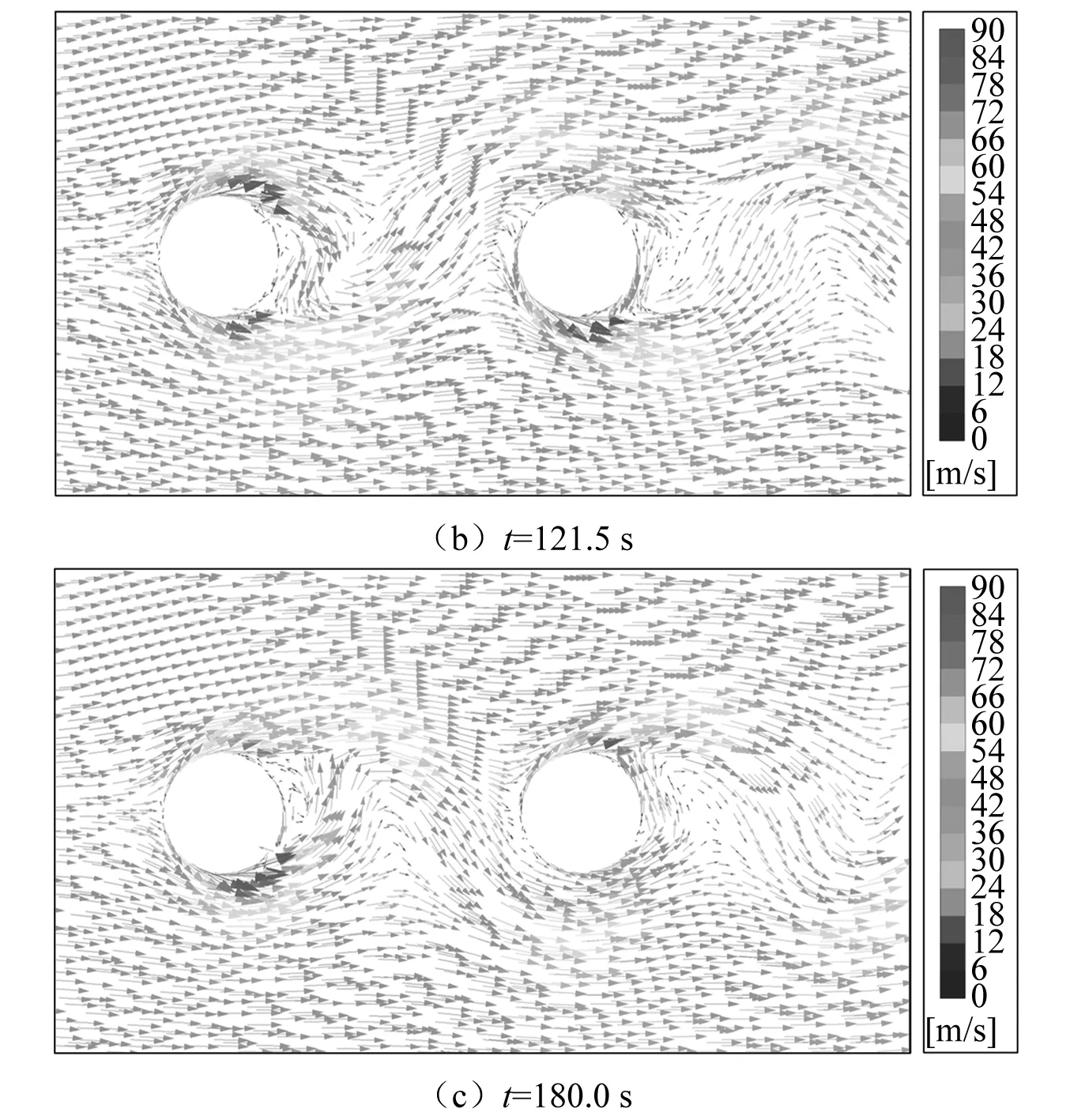
圖12 不同時刻邊跨雙主纜周圍風速矢量圖(U=38.5 m/s)Fig.12 Vector diagram of wind speed around the side span main cable at different time

邊跨背風主纜在常遇風速和高風速均勻流作用下都有可能發生尾流馳振。因此,如果采用四主纜方案,建議采用螺旋式、凹坑等抗風氣動控制措施對邊跨主纜進行處理,并采用風洞模型試驗對抗風措施的效果進行確認。

4 結 論

(1) 建立了均勻流作用下考慮主纜三維效應、主纜間氣動干擾效應和雙向流固耦合效應的四主纜懸索橋單側并置雙主纜振動分析方法。該方法將橋梁系統分解為主纜子系統和除主纜之外的子系統,采用振型分解法用主纜前幾階橫向和豎向振型近似表達主纜子系統的位移,建立模態坐標下主纜的運動方程,將不同高度處主纜氣動力用代表性位置主纜氣動力近似表達,采用流固耦合模型計算均勻流作用下代表性位置主纜氣動力,通過結構運動方程和流體動力學方程的雙向迭代求解最終獲得主纜子系統模態坐標和主纜的振動位移。

(2) 均勻流作用下主跨2 180 m四主纜單跨吊懸索橋成橋狀態中跨主纜的振動分析結果表明:不同風速作用下,中跨迎風主纜、背風主纜的振動頻率基本相當,但存在一定相位差;隨著風速增加,雙主纜之間的中心間距不斷減小,但最不利情況下(風速42.0 m/s),雙主纜間的中心間距遠大于雙主纜接觸時的最小凈矩,雙主纜間不會發生接觸。

(3) 均勻流作用下主跨2 180 m四主纜單跨吊懸索橋邊跨主纜的振動分析結果表明:特定風攻角下,邊跨背風主纜存在尾流馳振現象,建議采用螺旋式、凹坑等抗風控制措施對邊跨主纜進行處理。