基于廣域多時間尺度的CVT 誤差狀態(tài)預測方法
成躍宇 CHENG Yue-yu;成國鋒 CHENG Guo-feng
(國網揚州供電公司,揚州 225009)
0 引言
習近平總書記指出,世界經濟數(shù)字化轉型是大勢所趨。以數(shù)字化、網絡化、智能化為特征的新一代信息技術日益創(chuàng)新突破,正在推動全社會進入數(shù)字化時代。當前,我國各類計量器具的監(jiān)管和服務都逐步向信息化、智能化邁進,為此國務院出臺《計量發(fā)展規(guī)劃(2021-2035 年)》等文件,要求探索并推動計量法規(guī)數(shù)字化和管理創(chuàng)新化,“大力加強計量科技創(chuàng)新,加大基礎、前沿和應用領域計量薄弱環(huán)節(jié)技術研究,推動計量產學研協(xié)同創(chuàng)新。探索建立新型計量監(jiān)管模式和思路,推動計量制度改革,提升計量管理能力和水平。”
電容式電壓互感器(Capacitor Voltage Transformer,CVT)是一種用于測量高電壓系統(tǒng)中電壓的傳感器,其計量性能的可靠與穩(wěn)定性直接影響電力系統(tǒng)保護、測控和計量的可靠性,CVT 超差故障直接導致測量失準,嚴重超差還可能引起繼電保護裝置誤動作,后果嚴重。為此,國家出臺《JJG 1189.4-2022 測量用互感器第4 部分:電力電壓互感器》等檢定規(guī)程,要求對CVT 開展停電校驗,但傳統(tǒng)的離線檢定存在“檢測不及時、停電時間長、檢測成本高”等問題,亟需推動CVT 從按“周期檢測”向按“狀態(tài)評估”的轉變。
對于CVT 誤差狀態(tài)預測的研究,目前主要有以下幾個方向和方法:①統(tǒng)計模型,利用歷史數(shù)據(jù)和統(tǒng)計分析方法,建立CVT 誤差與一些關鍵參數(shù)(如溫度、濕度、頻率等)之間的關系模型。通過監(jiān)測這些參數(shù)的變化,預測CVT的誤差狀態(tài)。常見的統(tǒng)計模型包括回歸模型、時間序列模型等。②機器學習方法:使用機器學習算法(如支持向量機、神經網絡、決策樹等)來構建CVT 誤差狀態(tài)的預測模型。這些模型可以根據(jù)CVT 的歷史數(shù)據(jù)和其他相關數(shù)據(jù),學習CVT 誤差與輸入參數(shù)之間的潛在關系,并進行預測。③物理模型:基于CVT 的物理特性和工作原理,建立數(shù)學模型來描述CVT 的誤差特性。這些模型可以考慮CVT 的結構、電場分布、電容器性能等因素,從而預測CVT 的誤差狀態(tài)和變化。
但是現(xiàn)有的預測方法只考慮單一粒度構建時序模型,存在數(shù)據(jù)維度單一、預測精度低的問題,為此,本文提出了基于廣域多時間尺度的CVT 誤差狀態(tài)預測方法,從輸入特征構建和預測模型優(yōu)化兩個角度對廣域CVT 誤差狀態(tài)進行深入挖掘評估:在輸入特征構建方面,深入挖掘CVT的二次輸出數(shù)據(jù)的時序規(guī)律,采用STL 算法(Seasonal-Trend decomposition procedure based on Loess,基于局部加權回歸的周期趨勢分解)分解出趨勢項、周期項和余項,構建了多元時間特征,解決了數(shù)據(jù)維度單一的問題;在預測模型優(yōu)化方面,設計多層Transformer 結構,采用patch 尺寸來進行粒度控制,實現(xiàn)了任意粒度時間序列信息的建模,解決了可靠性差、預測精度低的問題。
1 CVT 誤差特性
CVT 的誤差特性通常可以分為2 個部分:比值差和相位差,具體定義如下:
其中,ε 表示CVT 的比值差,U1表示CVT 的一次電壓,U2表示CVT 的二次電壓,kr表示CVT 的額定變比,ρ表示CVT 的相位差,φ1表示CVT 的一次電壓的初相位,φ2表示CVT 二次電壓的初相位。CVT 的誤差特性限值如表1 所示。
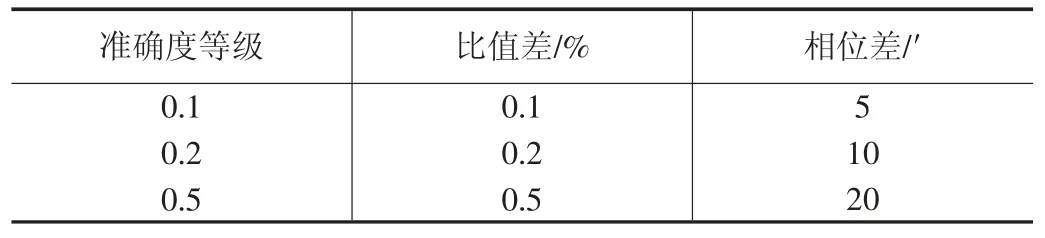
表1 CVT 基本誤差限值
當CVT 的誤差在基本誤差限值內,CVT 屬于正常狀態(tài);反之,超過基本誤差限值則處于異常狀態(tài)。
2 CVT 誤差狀態(tài)預測方法
2.1 總體技術路線
本文所提的基于廣域多時間尺度的CVT 誤差狀態(tài)預測方法的總體技術路線如圖1 所示,具體步驟如下:
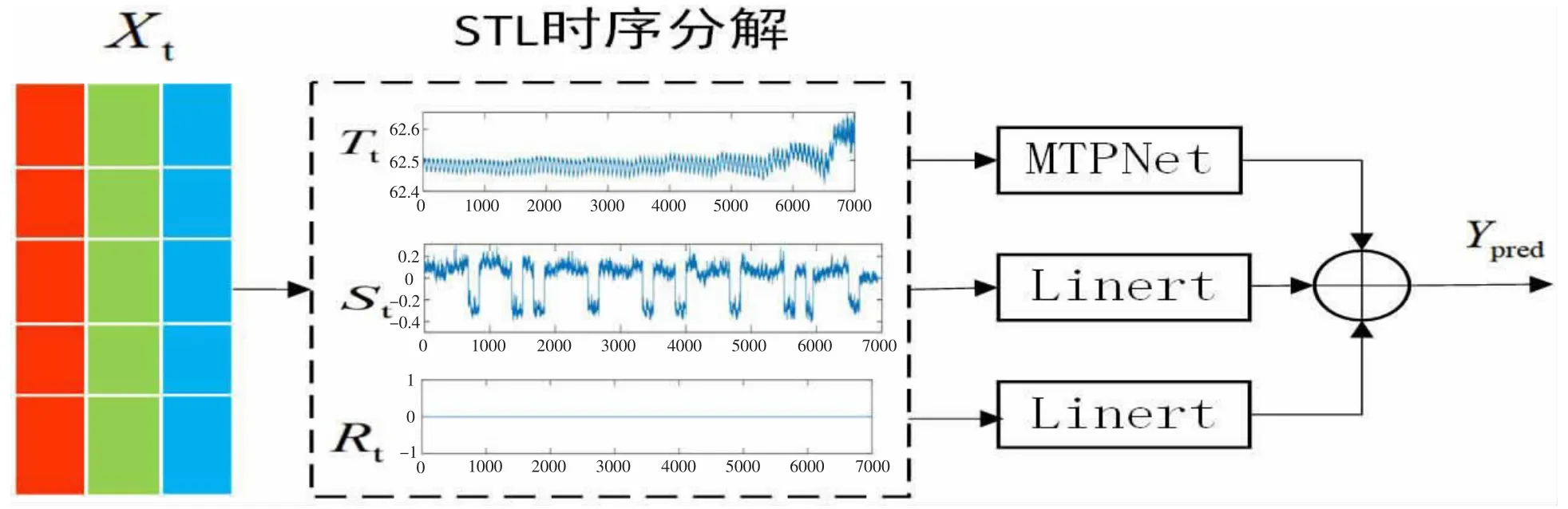
圖1 總體技術路線
①數(shù)據(jù)采集:使用準確度等級為0.05 級的電壓互感器在線采集裝置從變電站中控室計量屏柜中采集正常CVT 二次輸出數(shù)據(jù);
②提取特征:分析廣域CVT 二次輸出數(shù)據(jù)的時序規(guī)律,利用STL(Seasonal-Trend decomposition procedure based on Loess,基于局部加權回歸的周期趨勢分解)分解出趨勢項、周期項和余項,構建評估特征集;
③構建誤差預測模型:采用線性模型建模趨勢分量和余項,采用MTPNet(Multi-scale Transformer Pyramid Networks,多時間尺度變化的金字塔網絡)模型建模周期項,然后將三個預測模型進行融合,得到CVT 誤差狀態(tài)預測模型;
④預測誤差狀態(tài):將待測CVT 的二次輸出數(shù)據(jù)經處理后輸入至CVT 誤差狀態(tài)預測模型,實現(xiàn)CVT 運行誤差狀態(tài)的預測(正常狀態(tài)、告警狀態(tài)、異常狀態(tài))。
2.2 基于STL 的CVT 二次側數(shù)據(jù)的分解
CVT 的二次側數(shù)據(jù)Xt可被STL 分解為:
其中,Tt、St、Rt分別表示周期項、趨勢項、余項。
STL 的具體分解過程可以分為2 步:即內循環(huán)和外循環(huán)。在內循環(huán)迭代時,主要是利用平滑期更新St和Tt,去除各分量的異常擾動;外循環(huán)迭代時,主要擁有計算Rt。第i+1 次迭代的過程如下:
①對CVT 的二次側數(shù)據(jù)Xt進行去趨勢項處理:
其中,Xt(detrend)表示去趨勢項后的結果;Tt(i)表示趨勢分量第i 次迭代結果。
②子序列平滑。對每個子序列進行局部加權回歸(Lowess)平滑處理,前后各閆拓1 個時間點,組合得到新的子序列。
③采用低通濾波計算新實踐序列的趨勢項分量,去除周期性差異,然后由時間序列的可加性計算新時間序列的季節(jié)性分量,即:
④去除子序列中的季節(jié)分量,得到原始序列的季節(jié)分量和趨勢分量,即:
2.3 CVT 誤差狀態(tài)預測算法模型的構建
本文設計的CVT 誤差狀態(tài)預測算法模型算法框架如圖2 所示。
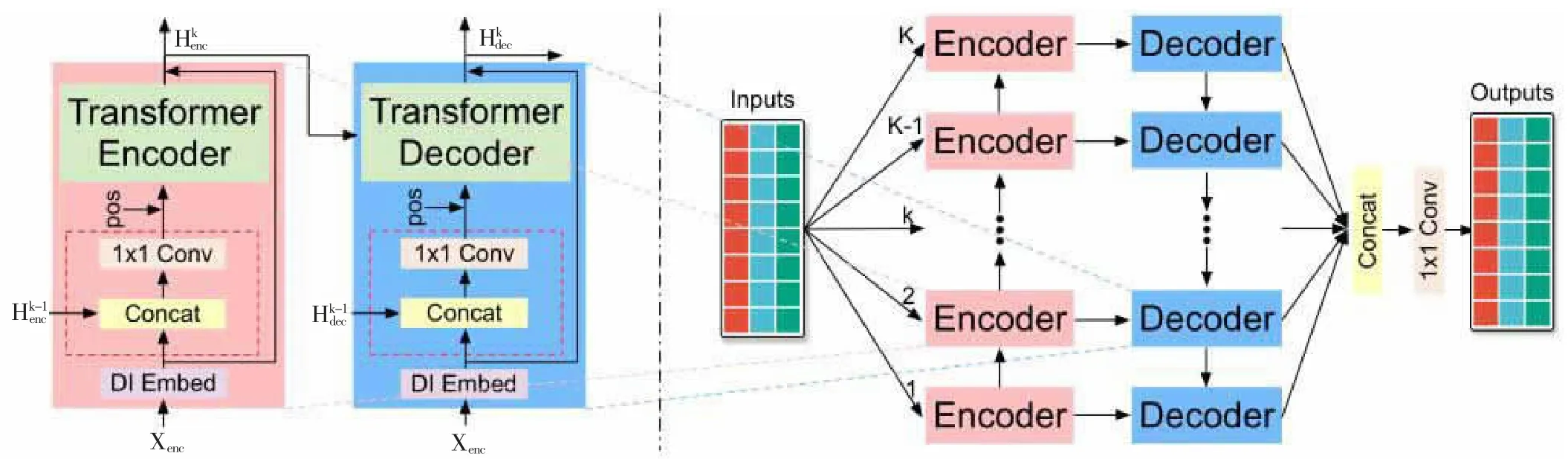
圖2 算法框架
從圖2 可知,MTPNet 包括多個變換器-編碼器-解碼器對,用于學習多個無約束尺度的時間相關性。為了實現(xiàn)不同粒度的建模,本文采用了patch 尺寸來控制時間粒度。K 層中每一層對應一種大小的patch size,基于這個patch size 進行DI embedding,可以實現(xiàn)不同粒度的信息提取。第k 層的信息會通過拼接的方式融合第k-1 層的編碼結果,計算過程如下,其中H 是上一層的編碼結果,X 是當前層使用對應patch size 得到的編碼:
Transformer 采用的是傳統(tǒng)的QKV 形式:
Encoder 和Decoder 都進行這種多粒度信息的建模,最終融合各個粒度的編碼結構得到最終的預測結果:
3 實驗驗證
實驗驗證了本方法在測試集的預測誤差,并通過與現(xiàn)有技術對比,證明了本文所提方法的優(yōu)越性。整個誤差評估實驗主要包括3 個部分:①實驗方案;②實驗評價指標;③實驗結果分析:1)基于STL 的時序數(shù)據(jù)分解實驗;2)對比實驗。
3.1 實驗方案
本文基于變電站現(xiàn)場采集的數(shù)據(jù)構建建模數(shù)據(jù)集,并利用人工加差的方式構建測試數(shù)據(jù)集,通過對比預測結果與加差結果說明本方法的有效性,實驗驗證方案如圖3所示。
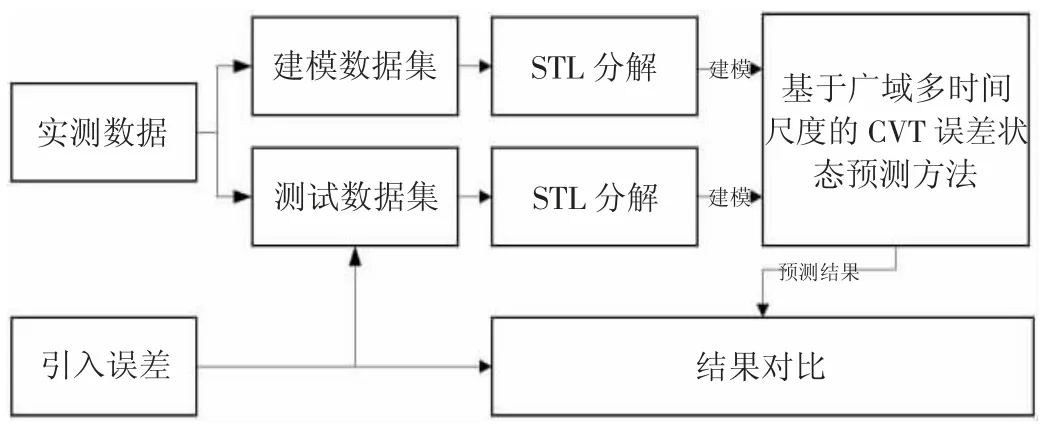
圖3 實驗驗證方案
3.2 實驗評價指標
為驗證本文方法(MTPNet)的有效性,選擇均方根誤差RMSE 和平均絕對誤差MAE 作為評價指標,RMSE 和MAE 的定義如下:
3.3 實驗結果分析
3.3.1 數(shù)據(jù)來源
本實驗的測試數(shù)據(jù)集采自某雙母線并列運行的220kV 變電站,采樣間隔為15 分鐘/次,數(shù)據(jù)時間跨度為720 天,從存儲數(shù)據(jù)中選擇7000 點測量數(shù)據(jù)構建實驗數(shù)據(jù)集,并利用軟件程序直接在測試數(shù)據(jù)集的數(shù)字量上添加人為誤差,構建的仿真實驗用實測數(shù)據(jù)如圖4 所示。
3.3.2 基于STL 的時序數(shù)據(jù)分解實驗
采用STL 算法對CVT 二次輸出數(shù)據(jù)進行分解,分解為周期項、趨勢項、余項,如圖5 所示。
3.3.3 不同輸入尺度下的算法性能對比實驗
為充分驗證本文所提出算法模型(MTPNet)的有效性和精確性,針對同一數(shù)據(jù)集,將其切分為24 天、36 天、48天、96 天、192 天、336 天、720 天的輸入長度,選擇PatchTST/64、Dlinear 分別進行CVT 誤差狀態(tài)預測,以驗證不同算法模型在誤差評估問題上的準確性,對比實驗結果如表2 所示。
從表2 可以看出,本文提出的算法在誤差狀態(tài)預測的問題上性能最佳,相比于PatchTST/64、Dlinear,RMSE 和MAE 顯著降低0.7%、2.69%。
3.3.4 不同工況下的算法性能對比實驗
為了進一步說明本文方法的有效性,對各個方法在不同工況下進行了前100 天的預測效果對比,如圖6 所示。
從圖6 可知,本文提出的算法不僅可以實時掌握CVT的動態(tài)變化趨勢,還可以適應復雜工況下電壓波動造成的預測曲線與實際值的偏差過大問題,適應范圍廣,預測精度高。
3.3.5 不同預測時間尺度下的算法性能對比實驗
不同預測時間尺度下的算法性能對比實驗如圖7所示。

圖7 不同預測時間尺度下的預測結果
本文方法在不同時間尺度預測上,預測精度和模型適應度均具有良好表現(xiàn),說明本文方法在捕獲二次側輸出數(shù)據(jù)的長期時間依賴性方面也具有一定的優(yōu)勢。
4 結語
本文提出了一種基于廣域多時間尺度的CVT 誤差狀態(tài)預測方法,有效提高了CVT 誤差狀態(tài)評估精度,相關結論如下:
①深度挖掘變電站在運CVT 群體二次輸出數(shù)據(jù),提出了多時空多尺度誤差狀態(tài)預測技術,采用STL 將二次輸出數(shù)據(jù)分解為趨勢分量、周期分量和余項,構建了多元時間序列鐵證;
②CVT 誤差狀態(tài)預測模型采用多層Transformer 結構,采用了patch 尺寸來控制,實現(xiàn)了任意粒度的時間序列信息建模;
③與現(xiàn)有的CVT 誤差評估模型相比,本文所提的預測模型,能有效實現(xiàn)多時間尺度的CVT 誤差狀態(tài)預測,相比于PatchTST/64、Dlinear,RMSE 和MAE 顯著降低0.7%、2.69%。
由于本方法是基于廣域數(shù)據(jù)驅動方法,不依賴于物理模型,因此同樣適用于CT、電能表等計量裝置,具有廣闊的應用前景。

