解三角形中的模型探究
吳瑋
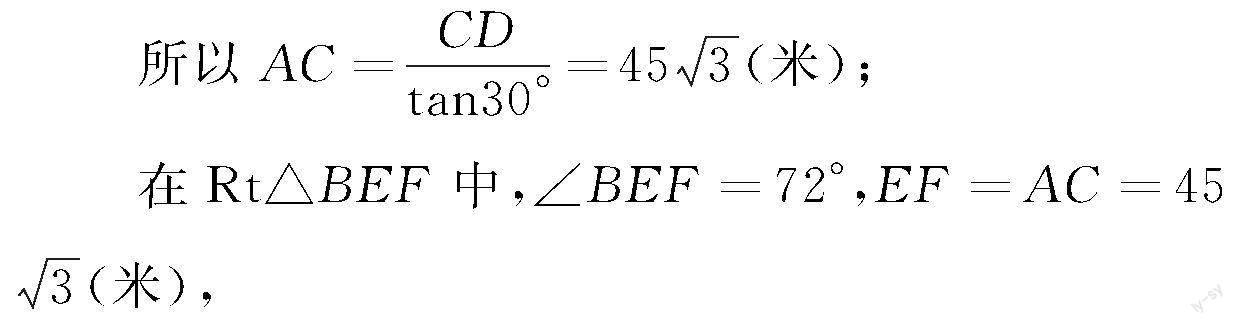
【摘要】解三角形問題時需引入幾何模型,常見的有“背靠背”型、“母抱子”型、“擁抱”型,探究學習要解讀模型,生成解題策略.本文探究分析三大解三角形模型,并結合實例開展應用探究,與讀者交流學習.
【關鍵詞】解三角形;“背靠背”型;“母抱子”型
解三角形是初中數學的重點問題,解題時常需要使用模型,如“背靠背”模型、“母抱子”模型、“擁抱”模型等,可利用模型的性質特征來轉化條件,構建思路,下面結合實例具體探究解三角形中的三大常用模型.
模型探究一 “背靠背”型
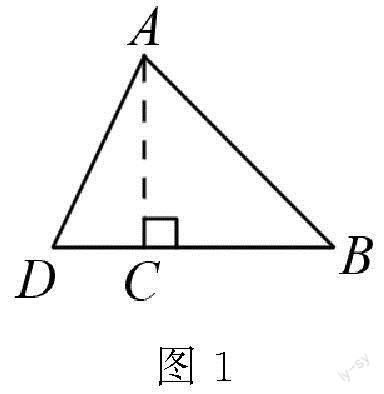
“背靠背”模型,即解三角形時構造兩個三角形“共側邊、反向靠”的模型.如圖1所示,解三角形ABD,此時可過點A作垂線AC,構造兩直角三角形:Rt△ACD和Rt△ACB.AC為兩直角三角形的公共邊,也是解題的關鍵,模型中有DC+CB=DB.
例1 如圖2(a),海中有個小島A,一艘輪船由西向東航行,在點B處測得小島A位于它的東北方向,此時輪船與小島相距20海里,繼續航行至點D處,測得小島A在它的北偏西60°方向,此時輪船與小島的距離AD為海里.
解析 本題目實則為解三角形ABD,可構造“背靠背”模型.過點A作AC⊥BD,如圖2(b),根據方位角及三角函數即可求解.
依題意可得∠ABC=45°,所以△ABC是等腰直角三角形,
AB=20(海里),則AC=BC=AB·sin45°=102(海里).
在Rt△ACD中,∠ADC=90°-60°=30°,
評析 上述解△ABD求AD長時構造了“背靠背”模型,Rt△ACD和Rt△ACB有公共邊AC,解三角形時充分利用進行線段長推導.
模型探究二 “母抱子”型
“母抱子”模型,即解三角形時構造兩個三角形“共側邊、同向靠”的模型,且兩個三角形有明顯大小差異.如圖3所示,解三角形ABD,此時可過點A作BC上的垂線AC,構造兩直角三角形:母型三角形——Rt△ACB、子型三角形——Rt△ACD.在兩個直角三角形中,AC為公共邊,有DC+BD=BC.
例2 如圖4(a),在一條筆直的海岸線l上有相距4km的A,B兩個觀測站,B站在A站的正東方向上,從A站測得船C在北偏東60°的方向上,從B站測得船C在北偏東30°的方向上,則船C到海岸線l的距離是km.
解析 本題目實則為解三角形ABC,求點C到l的距離,可構造“母抱子”模型.過點C作CD⊥AB于點D,如圖4(b)所示,后續根據等腰三角形的判定和性質解直角三角形即可求出答案.
根據題意可得∠CAD=90°-60°=30°,∠CBD=90°-30°=60°,
所以∠ACB=∠CBD-∠CAD=30°,
可推得∠CAB=∠ACB,
所以BC=AB=4km.
評析 上述解△ABC時,構造了“母抱子”模型,Rt△CBD和Rt△CAD為相互擁抱的結構,并有公共邊CD,解△ABC可求CB長,后續解Rt△CBD即可推出CD.
模型探究三 “擁抱”型
“擁抱”模型,即解三角形時構造兩個“底邊共線、定角相對、側邊平行”的模型.如圖5所示,Rt△ABC和Rt△BDC底邊共線,側邊AB和CD相平行,充分利用底邊BC(EF)進行轉化求線段長是解題的關鍵.
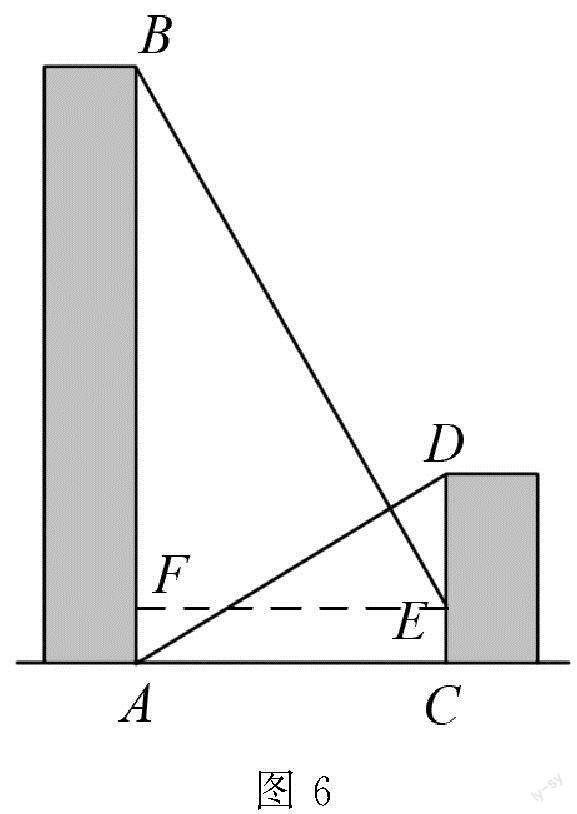
例3 大樓AB是某地標志性建筑,如圖6所示,某校九年級數學社團為測量大樓AB的高度,一小組先在附近一樓房CD的底端C點,用高為1.5米的
解析 本題目求線段AB長,可構造“擁抱”模型,過E作EF⊥AB于F,如圖6虛線所示.分析可知四邊形ACEF是矩形,所以EF=AC,AF=CE.
在Rt△ACD中,∠DAC=30°,CD=45(米),
所以BF=EF瘙簚tan72°=239.78(米),
可推知AB=BF+AF=239.78+1.5≈241.3(米),
即大樓AB的高為241.3米.
評析 上述解三角形時構造了“擁抱”型模型,Rt△ACD和Rt△BEF可視為是“相對擁抱”的結構,求解時充分利用底邊相等這一特殊條件,串聯兩直角三角形,進而求出AB長.
結語
總之,上述所探究的幾何模型在解三角形問題中有著廣泛的應用,探究學習中要從以下兩個視角進行:視角一,探究模型結構,總結結構性質,生成類型題的解題策略;視角二,探究模型應用,結合實例開展模型應用解析,總結解題方法.

