一元二次方程的常見解題技巧分析

秦怡雯

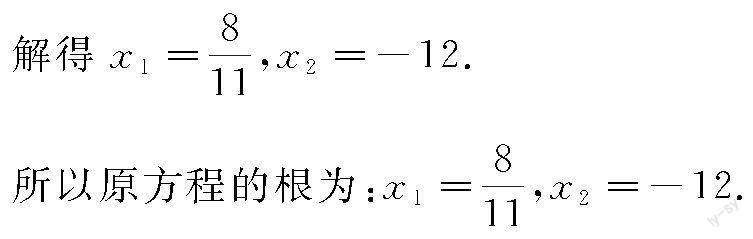
【摘要】一元二次方程的考查形式多種多樣，相關(guān)的問題也都十分靈活.常規(guī)的一元二次方程求解方法有：配方法、公式法、因式分解法等.因此，在解決此問題過程中，要靈活掌握基本方法，以不同試題進行分析，優(yōu)化解題思路.

【關(guān)鍵詞】一元二次方程；配方法、公式法

一元二次方程是中學(xué)數(shù)學(xué)的一個重要內(nèi)容，是歷年中考考核的重點.它既有獨立考查試題，也有廣泛滲透到其他方面的綜合考查.涉及的面非常廣，是教學(xué)的基礎(chǔ)也是重點.因此，掌握快速、精準地解題技巧顯得尤為重要.

1 公式法

公式法是利用求根公式直接求解，把一元二次方程的各系數(shù)代入求根公式，直接求出方程的解.公式法是解一元二次方程的一般方法，又叫萬能方法，對于任意一個一元二次方程，只要有解，就一定能用求根公式解出來[1].求根公式是用配方法解一元二次方程的結(jié)果，用它直接解方程可以避免繁雜的配方過程.解題思路大致為：①把方程化為一般形式；②確定a、b、c的值，計算b2－4ac的值；③當(dāng)b2－4ac≥0時，把a、b、c及b2－4ac的值代入一元二次方程的求根公式，求得方程的根；當(dāng)b2－4ac<0時，方程沒有實數(shù)根.如以下例題所示.

例1 解一元二次函數(shù)方程：2x2－3x+1=0.

解 由2x2－3x+1=0

可知a=2，b=－3，c=1.

所以Δ=b2－4ac=9-4×2×1=1>0，

2 因式分解法

因式分解法適合解特殊的一元二次方程，例如缺少常數(shù)項的或者形如x2+（p+q）x+pq=0的一元二次方程適用因式分解，用因式分解法解一元二次方程首先要進行因式分解，使方程化為兩個一次式的乘積等于0的形式，再使這兩個一次式分別等于0，從而實現(xiàn)降次.解題思路大致為：①將方程的右邊化為0，把左邊因式分解成兩個一次式的積；②令每個一次式都等于0，轉(zhuǎn)化為兩個一元一次方程；③解出這兩個一元一次方程，它們的解即為原方程的解[2].具體解題思路和步驟如以下例題所示.

例2 解一元二次函數(shù)方程：4（3x+1）2=25（x－2）2.

分析 該例題首先將方程的右邊化為0，移項將左邊因式分解成兩個一次式的積，令每個一次式都等于0，轉(zhuǎn)化為兩個一元一次方程，解出這兩個一元一次方程，它們的解即為原方程的解.

解 4（3x+1）2=25（x－2）2，

移項得：4（3x+1）2-25（x－2）2=0，

［2（3x+1）］2-［5（x－2）］2=0，

［2（3x+1）+5（x－2）］·［2（3x+1）-5（x－2）］=0，（11x-8）（x+12）=0，

所以11x-8=0或x+12=0，

3 配方法

配方法適用于解任意的一元二次方程，其是把一般形式的一元二次方程：ax2+bx+c=0 （a≥0）左端配成一個含有未知數(shù)的完全平方式，右端是一個非負常數(shù)，進而可用直接開平方法來求解.解題的大致思路為：①移項、二次項系數(shù)化成1；②配方，開平方進行運算即可.具體解題思路和步驟如以下例題所示.

例3 解一元二次函數(shù)方程：2x2－4x－m=0（m≥2）.

分析 該例題首先根據(jù)已知條件m>-2即可.移常數(shù)項，兩邊配上一次項系數(shù)一半的平方，轉(zhuǎn)化成（x+m）2=n的形式，由x>0，可知方程有實數(shù)根，最后開平方進行運算即可解出一元二次方程.

解 2x2－4x=m，

所以方程有實數(shù)根.

例4 解一元二次函數(shù)方程：x2+2x－4=0.

分析 該例題首先移常數(shù)項，兩邊配上一次項系數(shù)一半的平方，轉(zhuǎn)化成（x+m）2=n的形式，最后開平方根進行運算即可解出一元二次方程.

解 x2+2x－4=0，

x2+2x+（1）2=4+（1）2，

（x+1）2=5，

4 結(jié)語

根據(jù)上述不同的求解一元二次方程問題的例題分析，可以得到公式法、因式分解法以及配方法求一元二次方程的方法.針對不同類型問題，采取相對應(yīng)的解題方法進行解答.在解題過程中，同學(xué)們應(yīng)加強對問題條件的分析應(yīng)用，借助已知條件和相關(guān)性質(zhì)去靈活解答，以此提高解題的效率，讓同學(xué)們在考試中得心應(yīng)手，同時也希望同學(xué)們謹記各部分的注意事項，記住各種方法的適用范圍，以便在考試中能夠靈活運用，避免出現(xiàn)錯誤.

參考文獻：

［1］唐壽.淺談初中數(shù)學(xué)一元二次方程的解法及其應(yīng)用[J].基礎(chǔ)教育論壇， 2019（20）：40-41

［2］李晴.初中數(shù)學(xué)“融錯”教學(xué)智慧分享策略的研究——以“一元二次方程的解法復(fù)習(xí)”為例[J].上海中學(xué)數(shù)學(xué)， 2021（9）：35-37.