廣義納什均衡問題的精確指數—對數罰函數算法

楊 迪 何家文

1.南寧師范大學師園學院 廣西南寧 530226;2.南寧學院通識教育學院 廣西南寧 530200

納什均衡問題是博弈論中一種非常重要的研究類型。廣義納什均衡問題(Generalized Nash Equilibrium Problem,GNEP)是納什均衡問題的一種拓展形式,其中涉及的局中人決策影響其他局中人決策的情況,更能體現博弈問題中局中人之間普遍聯系的實際情況。近年來,全球范圍內經濟的發展和市場競爭日趨激烈,已經不再是單個局中人選擇策略就能達到最優策略的效果。單純的納什均衡問題已經不能滿足實際需求,越來越多的學者通過研究廣義納什均衡博弈相關問題,以求能更好地推動社會和經濟的發展。

本文在對指數精確罰函數和對數罰函數相關內容的基礎上,利用這兩個互為反函數的函數特征,提出一個指數—對數精確罰函數方法,用以求得廣義納什均衡(縮寫為GNE),從而解決GNEP。

常用的約束最小值問題為:

minf(x)
s.t.gi(x)≤0.i=1,…,m,

(1)

其中f(x),gi(x):Rn→R是連續可微函數。

針對問題(1),文獻[1]提出了一個聯合指數罰函數法。這個方法在運行初始是不需要內點初始點,在選擇初始點時有很大的選擇空間,這樣也能得到一個解,這是這個算法的優勢,可惜效果跟內點法相似,不一定得到精確解。在文獻[2]中,針對凸規劃,利用精確指數乘子函數,也得到一個最優解。在前文基礎型上,文獻[3]則提出了一個精確的對數—指數乘子罰函數,得到一個較好的結果,這對提出新的罰函數算法給出了一個很好的示范。文獻[4]利用指數型懲罰函數,對部分耦合約束進行懲罰,將廣義納什均衡問題的求解轉化為求解一系列光滑的懲罰納什均衡,進而得到想要的結果。文獻[5-6]在研究串聯機械臂系統軌跡規劃問題、復雜的大規模極大極小值問題中,提出聯合指數或對數罰函數法進行操作,給出相關算法的實際應用價值。這些學者在利用指數或對數罰函數來求解相關問題都做了有益的嘗試,有利于我們進一步對廣義納什均衡問題進行探討。

1 預備知識

假設博弈中有N個局中人,每一個局中人v∈{1,…,N}都有自己的策略集Xv,從自己的策略集Xv中選取一個策略xv。將每個局中人給出的策略形成一個組合,由此得到博弈中N個局中人的一個策略組合x=(x1,…,xN)。為突出我們所研究的某個局中人v的策略xv,記x=(xv,x-v),其中x-v=(x1,…,xv-1,xv+1,…,xN)表示除了局中人v之外,其他局中人所選擇的策略形成的組合。我們以策略組合x為元素,構成局中人策略的集合,記為局中人策略集的笛卡爾積X,即x∈X:=X1×…×XN,并稱X為局中人的策略組合集。令θv:Rn→R為博弈中每個局中人v的目標函數,為了更好地分析,假設θv(xv,x-v)對xv為凸。如果x*,v滿足對v=1,…,N,(NEP)θv(x*,v,x*,-v)≤θv(xv,x*,-v),?xv∈Xv。則向量x*=(x*,v,x*,-v)∈X稱為一個納什均衡(Nash Equilibrium,NE)。上述問題就是納什均衡問題(Nash Equilibrium Problem,NEP)。

對現實當中的很多情況,博弈中的每個局中人在選擇的策略的過程中,不僅要考慮自身情況,還要考慮其他局中人所選擇的策略,由此來得到自身最大的收益或者付出最小的代價。為表示局中人在策略選擇過程中策略之間的相關性,將每個局中人v的策略集表示為Xv(x-v):={xv|(xv,x-v)∈X},由此特別定義策略集組合集為Ω(x):=X1(x-1)×…×XN(x-N)。如果x*,v滿足對v=1,…,N,(GNEP)θv(x*,v,x*.-v)≤θv(xv,x*,-v),?xv∈Xv(x-v)。稱向量x*∈Ω為一個廣義納什均衡(GNE),此問題就是本文重點要研究的廣義納什均衡問題(GNEP)。

在GNEP中,每一個局中人選擇的策略與競爭對手所選擇的策略是有相關性的。這更體現出在一些實際博弈中,局中人在進行策略選擇時的相互影響。

針對GNEP,本文考慮了約束是不等式組的情況。在約束中,其中一部分是局中人v=1,…,N選擇的策略依賴于其他局中人所選策略的約束,簡稱為依賴約束;另一種就是獨立約束,即每個局中人的策略不依賴其他局中人的策略選擇的約束。

針對局中人v,本文考慮的GNEP,只有依賴約束的最小值問題:

minxvθv(xv,x-v)
s.t.gv(xv,x-v)≤0,

(2)

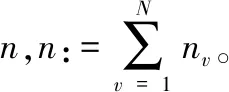
Xv(x-v):={xv|gv(xv,x-v)≤0}

對所有v=1,…,N,針對原問題(2)需要一個全局假設:(1)目標函數θv:Rn→R是連續可微的,并且對所給xv為凸;(2)約束條件gv:Rn→R對所有i=1,…,m是連續可微的,并且對xv為凸。

2 精確指數—對數罰函數算法及其收斂性證明

針對廣義納什均衡問題(2),本文設計一個新的精確指數—對數罰函數:

由此得到一個精確指數—對數罰問題:

minxvMv(x,ρv)

(3)

經過分析計算,可得目標函數的梯度為:

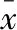
如果出現這樣的情況,就可以通過增大罰參數來強迫可行性,直至找到合適的解。

根據以上分析,給出精確指數—對數罰函數算法1。

算法1

步驟1 若xk是GNEP的解。停止。

步驟2 若xk不可行,且對任意v,若

(4)

則對所有v,使罰參數ρv加倍,令k←k+1,轉步驟1。

下面證明原問題(2)與罰問題(3)是等價的。

定理1 如果算法1是有限步終止迭代,則原問題(2)的解與問題(3)的解等價。

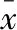
反過來,要證問題(3)的解x*為(2)的解,我們只需證明x*為可行點。假設x*是不可行點,M(x,ρ*)在x*的鄰域上連續可微,有:

0=?xvM(x*,ρ*)

血管淋巴管瘤合并血管瘤屬于特殊類型之一，就目前而言，臨床報道較少，多以個案報道為主。影像學檢查發現，以淋巴管和血管構成比不同而表不一為主，其中淋巴管患者的表現類似于淋巴瘤患者，血管瘤患者的表現類似于血管瘤。王小巖[10]在相關報道中發現，脾臟血管淋巴管瘤3例患者中，CT檢查顯示血管瘤樣強化特征共計2例。瘤體內有出血表現時則清晰可見“液-液”平面現象。

故有:

算法1要求cv∈(0,1),那么對某些v和充分大的k,必定都會滿足(4),根據算法1要求,更新罰參數,與題設條件產生矛盾。由此可得x*是可行點,而x*是可行點,就有問題(3)的解x*為(2)的解,本定理得證。

根據文獻[3-4],我們新定義一些約束規格CQγ:

定義1 定義

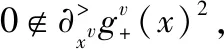
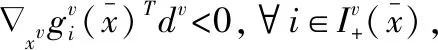
定理2 假設由算法1產生的序列{xk}有界,對以下3個結論:(a)在xk的極限處,MFCQ成立,則CQ0條件成立;(b)在xk的極限處,CQ0條件成立,則罰參數只更新有限次。

對其中適當的子列,有下面的結論:

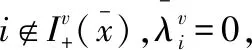
由于滿足EMFCQ條件,當等式兩邊同時乘以dv時,就可以給出:

顯然這是矛盾的。因此(a)成立。

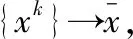
3 數值結果

接下來的數值例子來說明算法1的可行性和有效性。

例1 考慮N=2的博弈:

其中局中人v=1決策變量為x1,局中人v=2的決策變量為x2,他們所受的共享約束是g(x1,x2)=x1+x2-1≤0。可得此博弈的最優解集為:

由此可以看出對α∈[1/2,1],本例是有無窮多個解(α,1-α)。根據文獻[7],例1有唯一的變分均衡點(3/4,1/4)。

表1中p和pel分別表示經典罰函數算法和算法1,初始罰參數設置為ρ0=2。表1的數據表明,本文所提出的算法與經典罰函數相比,在迭代步數和時間上法不相上下,對任取初始點,都能得到有效數據。這說明提出的新算法是可行且穩定有效的。表1的數據也表明,在同樣的誤差內,算法1得到的解要比經典算法更為精確,這是新算法的優勢所在。即在比較大的誤差范圍內(如ε=1.0e-3),算法1仍能保證最終迭代點與最優點的基本一致,比經典算法更加精確且迭代時間更短。

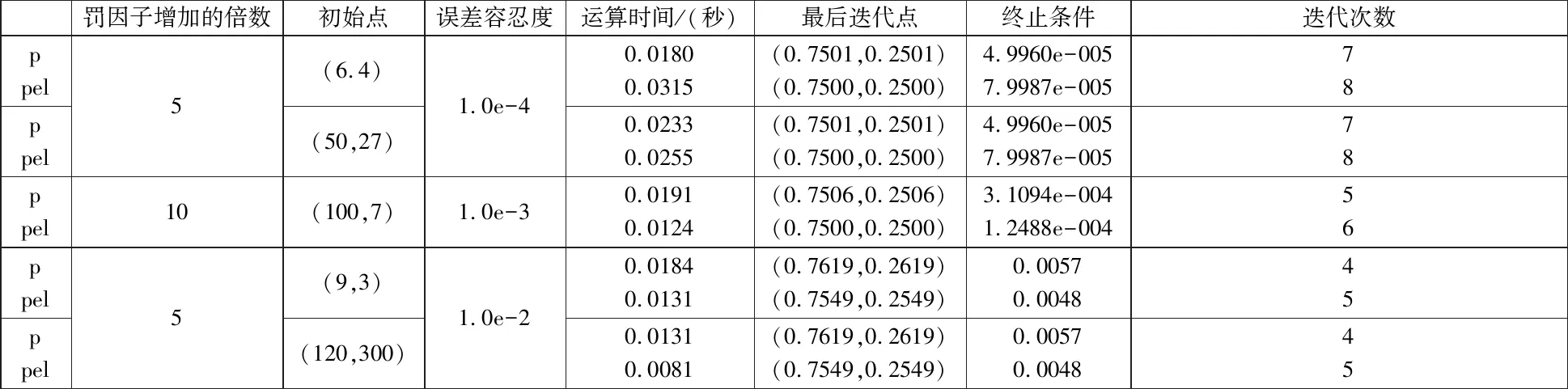
表1算法1和經典的罰函數算法得出的實驗結果1

例2 考慮N=2的博弈:

局中人v=1的決策變量為x1,局中人v=2的決策變量為x2。他們有共同的約束g(x1,x2)=x1+x2-1≤0。分析可知例2唯一的最優點為x=(0,1),由此得到最優值-3。數值實驗如下面的表2所示。

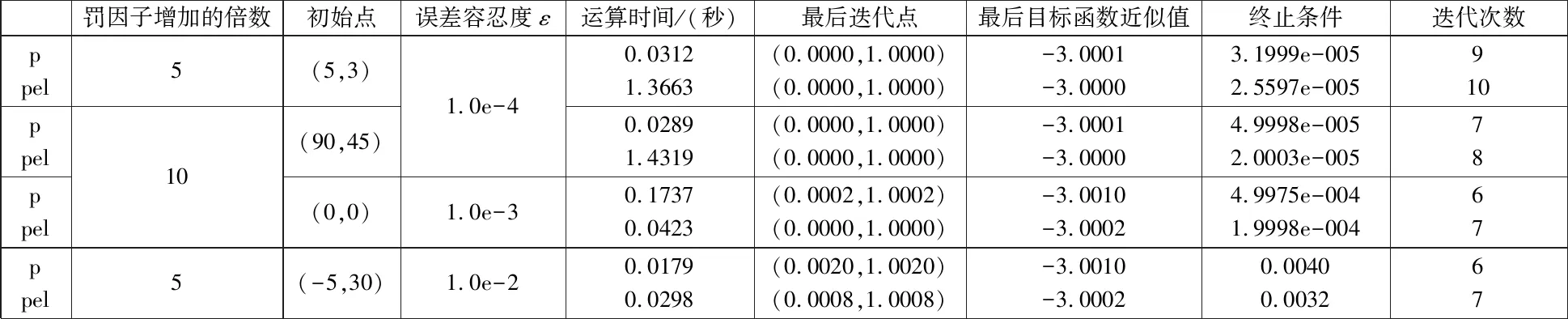
表2 算法1和經典的罰函數算法得出的實驗結果1

從表2數據中可看出,在比較大的誤差范圍內,本文提出的新算法得到的解要比經典算法更為精確。通過綜合表1與表2的數據,也可以看出在比較大的誤差范圍內,新算法得到的解要比經典算法更為精確,在多數情況下,迭代時間也要更短。這就意味著,在實際情況中,算法1滿足在較低的要求下,仍然可以得到經典罰函數算法在高要求下才得到的解。這樣就更能貼近現實生活的需求,顯然是本文罰函數算法的優勢所在。

結語

本文主要是利用精確罰函數方法來求解廣義納什均衡問題,針對不等式約束,提出了一個精確的指數—對數罰函數算法,并通過討論算法的全局收斂性,給出數值結果來說明算法的有效性與可行性。

隨著社會的發展,廣義納什均衡問題在現實世界中各個領域的應用越來越多,意味著我們需要解決具有各式各樣要求的問題,并且這些問題內部聯系越來越緊密。現有求解GNEP的罰函數算法都具有一定的局限性,與實際應用還存在一定的距離。往后,我們的研究方向仍有很多,比如,對更一般目標問題,像目標函數不為凸函數或約束函數不是凸函數的情況,還可提出對不是凸規劃的算法等。