大質量數差雙組分氣體混合物流場及豐度場的數值研究

田松杰,顧志勇,郭子學

(核工業理化工程研究院,天津 300180)

利用旋轉圓筒生產同位素時,由于原料本身或工藝的問題,不可避免地會產生輕組分氣體[1-2]。由于輕氣體的摩爾質量通常遠小于同位素氣體的摩爾質量,容易向圓筒的輕餾分端聚集。輕氣體的引入不僅影響同位素的生產效果,影響同位素產品質量,高含量的輕組分氣體還會危害旋轉圓筒的安全運行。為了保證旋轉圓筒連續運行,需要對圓筒中富集的輕氣體進行去除。為有效去除輕氣體,核工業理化工程研究院正在研制旋轉圓筒,研究大質量數差雙組分氣體混合物的流場及豐度場對進一步認識該旋轉圓筒的工作機理、深入掌握影響旋轉圓筒性能的設計參數、提高旋轉圓筒的研制效率具有重要意義。

在研究旋轉圓筒中同位素混合氣體的流場及豐度場時,由于同位素之間的質量數差很小,通常利用同位素混合物的組分具有幾乎一樣物理化學性質的特點,根據同位素近似可把混合物視為單一流體,先單獨求解單一氣體混合物的流動方程,然后利用所求得的流場,對豐度未知的擴散方程進行求解[3-4]。然而,當氣體混合物的質量數差別很大時,同位素近似不再有效。混合氣體的各組分在物理性質上有明顯差異,除混合氣體的密度隨豐度變化外,氣體的物性參數也與豐度有關。混合氣體的豐度分布受對流和擴散兩種質量輸運過程影響[5-9]。因此,耦合求解流動方程與擴散方程,進行大質量數差氣體混合物流場及豐度場的數值研究非常必要。

質量數差較大氣體混合物的理論研究較少,公開發表的研究中,Kai[10]采用修正的牛頓法在低轉速小擾動條件下得到收斂的解,但其密度條件的給法會在邊界處產生擴散流通量。鄭直[11]采用牛頓法在忽略能量方程耗散項的情況下同樣只得到了小擾動下的解。本研究以歸一化后質量數為0.93和0.07的雙組分氣體混合物為研究對象,確定大質量數差雙組分氣體混合物物性參數的計算方法,參考文獻中同倫延拓修正的牛頓法[12]耦合求解強擾動下的流動方程與擴散方程,并通過復合密度邊界條件確保混合氣體在邊界處無質量通量,得到強擾動下高速旋轉圓筒中混合氣體流體動力學方程組收斂的解,給出混合氣體在旋轉圓筒中流場及豐度場的分布情況,探究側壁溫度驅動、機械驅動對氣體混合物流場及豐度場的影響。

1 雙組分氣體混合物的流體動力學方程組

針對粘性可壓縮雙組分氣體混合物在旋轉圓筒中的運動,在二維軸對稱坐標系中,穩態無源匯的雙組分氣體混合物流體動力學方程組形式如下[10]:

(1)

(2)

(3)

(4)

(5)

(6)

式中,r、z為徑向和軸向坐標距離;ρ1、ρ2為兩組分的密度;T為混合氣體的溫度;u、v、w為質量平均速度的徑向、角向與軸向的分量;Cv1、Cv2為兩組分的定容熱容;λ為熱傳導系數;n為單位體積內混合氣體的摩爾數;D12為二元擴散系數;M1、M2為兩組分的摩爾質量;R為氣體常數;ρ1、ρ2、u、v、w、T是未知量。求得混合物氣體質量平均速度后,可根據擴散流定義Ji=ρi(vi-v)(i=1,2)求得各組分的速度分布。

公式(1)為連續性方程;動量方程(2)～(4)中的Gr、Gθ、Gz表示的是粘性項,認為混合物為一種具有混合粘性系數的氣體;能量方程(5)中的De是熱傳導項,φ是耗散項;公式(6)為擴散方程。這些項的具體形式如下:

(7)

(8)

(9)

(10)

(11)

2 雙組分氣體混合物的物性參數計算方法

混合氣體的物性參數對于方程的求解至關重要,因此對旋轉圓筒中雙組分氣體混合物物性參數的計算方法進行討論。

混合氣體的粘性系數可由氣體輸運理論[13]得到,計算公式為:

(12)

其中

(13)

(14)

(15)

(16)

(17)

(i=1,2)

(18)

(19)

定壓熱容Cp1,Cp2是與溫度T有關的量,按經驗公式[10]計算:

對于重組分氣體:

(20)

對于輕組分氣體:

(21)

定容熱容Cv1、Cv2由邁耶公式[14]求得:

Cvi=Cpi-R/Mi, (i=1,2)

(22)

熱傳導系數λ由下式[10]進行計算:

(23)

式中:

(24)

擴散系數nD12由下式[12]計算:

nD12=1.858 3×10-7×1.01×

(25)

由以上計算公式可知,混合氣體的物性參數是豐度和溫度的函數。在實際計算中,先以等溫剛體狀態下氣體混合物在圓筒中的溫度和豐度作為物性參數計算的初值,不斷對所得到的解進行校準,即用第k-1次迭代中得到的溫度值和豐度值,計算第k次迭代時氣體混合物的物性參數,在沒有達到迭代精度時,迭代重復進行。

3 邊界條件與定解條件

3.1 邊界條件

高速旋轉圓筒內部強旋流場造成氣體密度沿徑向呈指數分布,從圓筒軸線到側壁形成了流動分區。在圓筒軸線附近的是分子流區,然后是過渡流區,側壁附近的是粘性流區,其內部的流動特征相當復雜。在計算時,由于大部分氣體受慣性力作用集中于圓筒側壁附近,因此選取的計算區域為側壁附近的粘性流區。在計算域的邊界上要給定邊界條件,而根據性質的不同,旋轉圓筒內部流場計算域的邊界分為固體壁面邊界和內邊界兩類(圖1)。

圖1 旋轉圓筒軸對稱計算模型示意圖Fig.1 Schematic diagram of axisymmetric calculation model for a rotating cylinder

第一種邊界是固體壁面,包括旋轉圓筒上固壁、下固壁及側壁。在固體壁面邊界處,由于流體的粘性作用,速度和溫度應當滿足無滑移邊界條件:

u=0,v=rω,w=0,T=Tw

(26)

其中,rω為壁面的角向運動速度,Tw為壁面溫度。計算中通過對壁面施加邊界條件實現側壁熱驅動和機械驅動。其中側壁熱驅動為線性分布,上端溫度低而下端溫度高,壁面溫度Tw=T0-(z/H-1/2)ΔTw,上、下壁面溫度均勻分布,T0為圓筒內氣體的平均溫度,ΔTw為圓筒側壁溫度驅動的參數值。機械驅動使用等效圓盤模型近似,在下固壁邊界用一個角向速度滯后于圓筒轉速Δω的無限薄圓盤模擬部件對氣體的滯止作用,定義機械驅動系數Δω*=Δω/ω。

第二種邊界稱為內邊界,這是連續介質假設瀕臨失效的極限位置。在內邊界上,速度和溫度為中心自由邊界,即滿足條件:

(27)

在數值計算中,不能僅對速度和溫度給邊界條件,因為任何一個離散網格上都同時有著6個獨立未知量,邊界上的網格也不例外,如果只有以上兩式,將缺少2個密度邊界條件而無法定解。全回流情況下,滿足無對流通量和無擴散通量這兩個條件,才能保證重組分和輕組分在邊界上都沒有出入。無對流通量可以由混合氣體在邊界處法向速度為0的條件保證,而擴散通量大小由式(6)擴散方程的擴散項決定,因此要滿足混合氣體在邊界處無擴散必須有如下方程成立:

(28)

該方程不能完全約束兩組分的密度邊界,還需要給一個混合氣體滑移密度邊界條件:

(29)

(28)和(29)兩式共同構成了雙組分氣體混合物密度的邊界條件。

3.2 定解條件

確定無對流通量和無擴散通量的邊界條件后,計算區域內所有網格的連續性方程之和為0=0,所有網格的擴散方程之和也為0=0,即存在一個連續性方程和其他的連續性方程線性相關,同樣存在一個擴散方程和其他的擴散方程線性相關,數值計算時需要對連續性方程和擴散方程施加約束條件。在全回流情況下,圓筒內的重組分、輕組分滯留量不變,滯留量約束條件形式如下:

(30)

(31)

H01和H02是兩個組分的初始滯留量,用以上兩個滯留量方程替換計算區域內的一個連續性方程和一個擴散方程,構成定解條件。

4 數值模擬結果與分析

本研究以歸一化后質量數為0.93和0.07的雙組分氣體混合物為研究對象,計算流場和豐度場所用的算例參數列于表1。

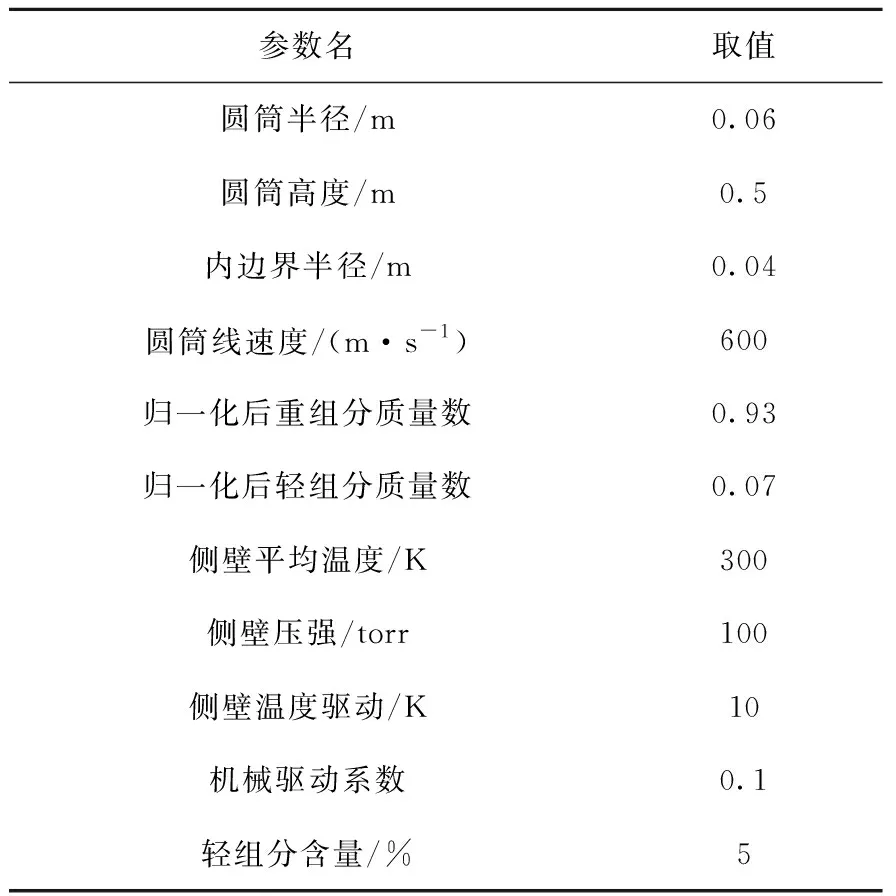
表1 算例用到的計算參數Table 1 Calculation parameters used in example

旋轉圓筒中雙組分氣體混合物的流線圖示于圖2。由圖2a可見,由于重組分分子量較大,在旋轉圓筒中存在較大的密度梯度,因此重組分的大部分環流集中在靠近側壁的Stewardson(斯圖爾森)層。由圖2b可見,輕組分分子量較小,在旋轉圓筒中密度梯度較小,環流并不會完全集中于側壁。在側壁溫度驅動、機械驅動和重組分環流共同作用下,輕組分在整個計算域內形成較大的環流。在靠近側壁處輕組分的環流受到重組分的強烈影響呈現出和重組分相似的靠近邊界層的軸向環流,而在計算域的中間位置形成和側壁環流方向相同的大環流。輕組分氣體的環流在深藍色區域沒有完全閉合,由網格數不夠引起。

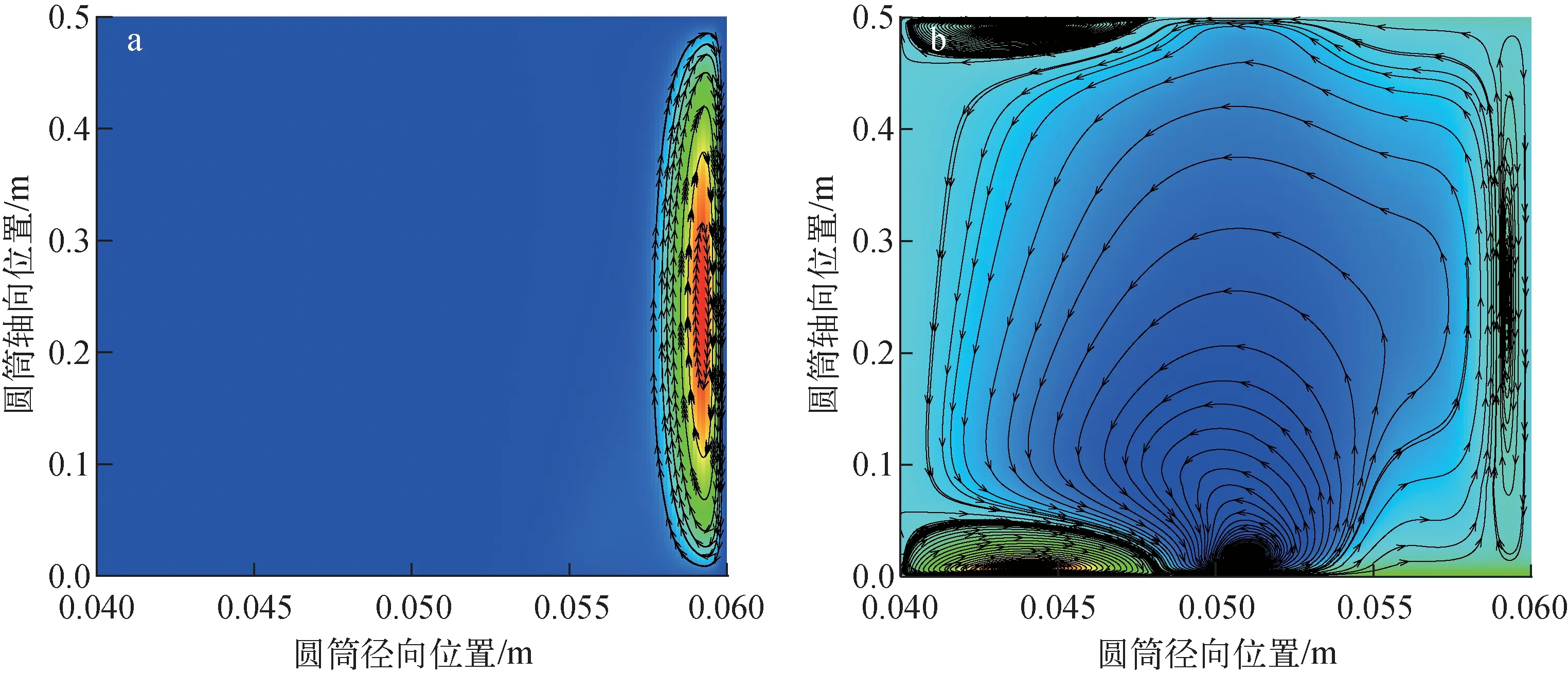
a——重組分流線圖;b——輕組分流線圖圖2 雙組分氣體混合物的流線圖Fig.2 Streamline diagram of the binary gas mixture

1 K側壁溫度驅動下網格加密前后輕組分氣體的流線圖示于圖3。由圖3a可見,網格數為3萬情況下,輕組分氣體在深藍色區域流線不閉合。圖3b網格數加密到6萬后,流線完全閉合。產生該現象的原因是:對于重組分氣體,環流主要集中在側壁,對靠近側壁的邊界層網格加密就可以分析重組分氣體的主要流動狀態,但是對于輕組分氣體,驅動引起的環流分布于整個計算域,分析輕組分氣體的流動狀態需要對整個計算域網格加密。

a——150×200網格輕組分流線圖;b——200×300網格輕組分流線圖圖3 1K側壁溫度驅動下網格加密前后輕組分氣體的流線圖Fig.3 Streamline diagram of the light component gases before and after grid refinement driven by 1K sidewall temperature

較強驅動作用下輕組分氣體在整個計算域的流動狀態更復雜,需要的網格數更多。本研究算例的網格數約為4萬,若對整個計算域加密網格數估算在25萬以上,計算量遠超過普通計算機的計算能力。網格數為4萬和網格數為8萬情況下,在圓筒總高度1/2截面上輕組分氣體的軸向質量通量分布曲線示于圖4。由圖4可見,網格數增加1倍,輕組分氣體的軸向質量通量幾乎沒有變化,本研究算例在該網格條件下的計算結果準確可靠。

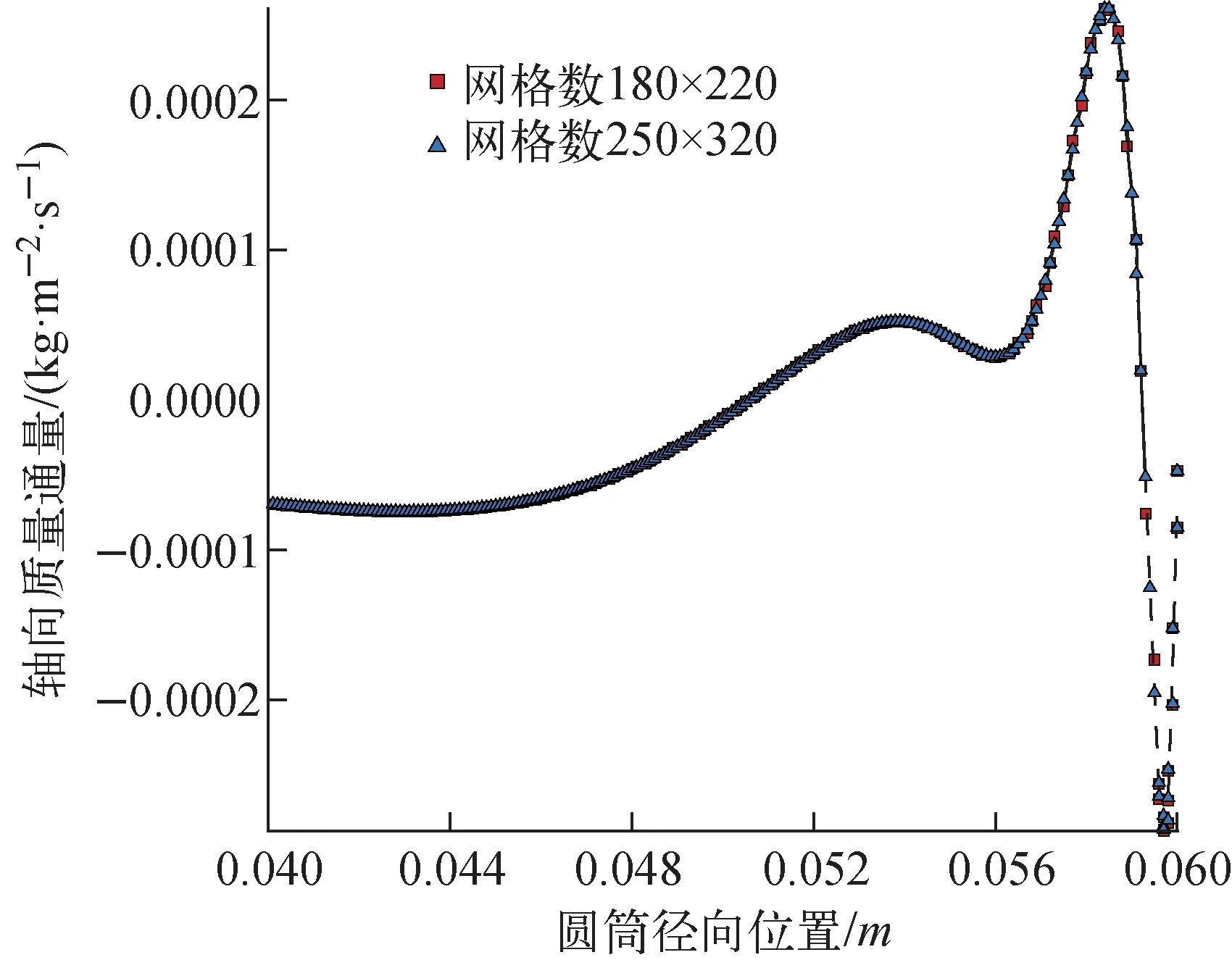
圖4 網格加密前后輕組分氣體的軸向質量通量分布曲線Fig.4 Axial mass flux curve of the light component gases before and after grid refinement

軸向位置為圓筒總高度(z/H)1/4、1/2和3/4橫截面上氣體混合物各組分的軸向質量通量分布曲線示于圖5。計算結果表明,各組分氣體在不同橫截面上的軸向質量通量分布曲線的形狀基本相同,而沿軸向存在幅度變化。重組分在圓筒軸向的中間幅度最大,兩端逐漸減小。輕組分在靠近側壁處曲線分布形狀和重組分相似,在計算域中間位置受側壁溫度驅動影響較小而受機械驅動影響較大,環流量沿軸向高度由下而上逐漸減小。

a——重組分軸線質量通量分布曲線;b——輕組分軸向質量通量分布曲線圖5 雙組分氣體混合物的軸向質量通量分布曲線Fig.5 Axial mass flux curve of the binary gas mixture

旋轉圓筒中輕組分的摩爾豐度示于圖6。在旋轉圓筒中,大質量數差氣體混合物徑向豐度梯度較強而軸向豐度梯度較弱,即使是較強的側壁溫度驅動和機械驅動也很難改變這種徑向分離的性質,這與同位素混合物豐度梯度在軸向較強而徑向較弱的分布性質相反。

圖6 輕組分的摩爾豐度圖Fig.6 Molar abundance diagram of the light component in example

為探究各驅動對旋轉圓筒中混合氣體豐度場的影響,計算側壁溫度驅動和機械驅動單獨作用時混合氣體的軸向豐度梯度,結果示于圖7。由圖7可知,圓筒總高度的1/2橫截面處,混合氣體的軸向豐度梯度隨側壁溫度驅動和機械驅動增加的變化曲線。隨著側壁溫度驅動或機械驅動系數的增加,富集輕重組分的環流逐漸增強,混合氣體的軸向豐度梯度逐漸增大。

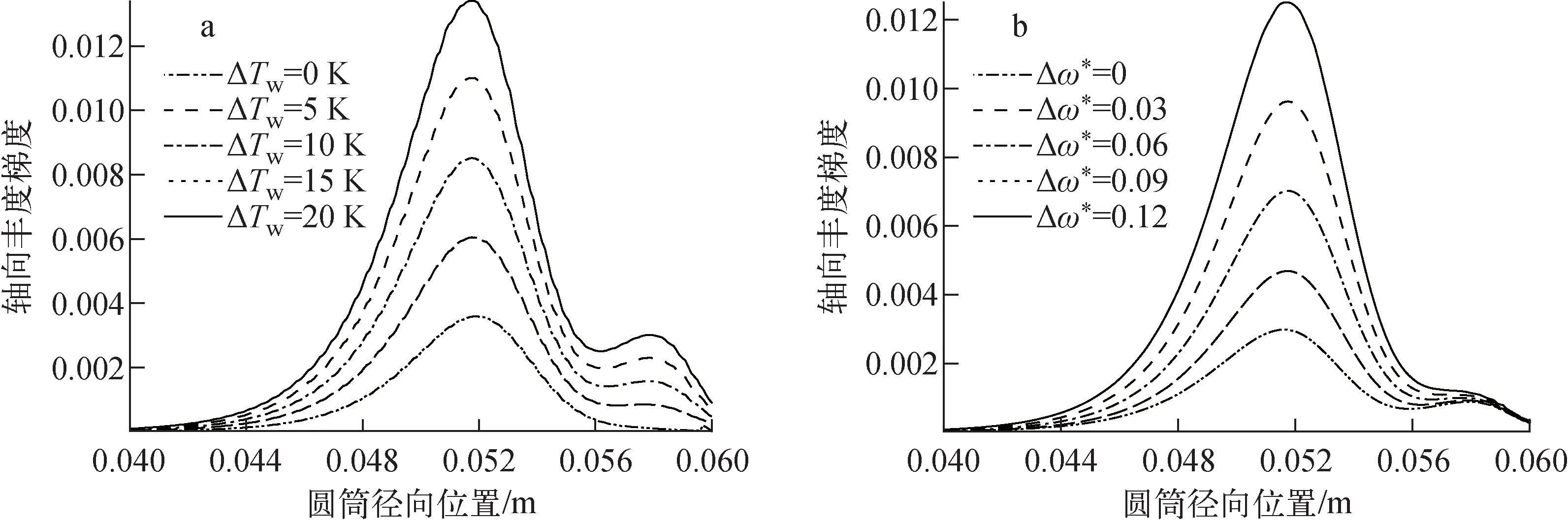
a——側壁溫度驅動;b——機械驅動系數圖7 軸向豐度梯度隨各驅動量變化的分布曲線Fig.7 Distribution curve of axial abundance gradient with changes in various drives

5 結論

本研究以歸一化后質量數為0.93和0.07的雙組分氣體混合物為研究對象,確定了大質量數差雙組分氣體混合物物性參數的計算方法,實現了耦合求解高轉速強擾動條件下的流動方程與擴散方程,得到了旋轉圓筒中大質量數差雙組分氣體混合物的流場及豐度場,并探究了側壁溫度驅動和機械驅動對混合氣體豐度場的影響,得出以下結論。

1) 雙組分氣體混合物中重組分環流集中于圓筒側壁,而輕組分環流分布于整個計算域。

2) 大質量數差雙組分氣體混合物的豐度分布受環流影響較小,氣體混合物在較強的驅動環流作用下仍呈現徑向分離的性質。

3) 混合氣體的軸向豐度梯度隨側壁溫度驅動的增加而增大,隨機械驅動的增加而增大。