一種利用SAHP-云模型的科技投入項目績效評估方法分析

馬威， 李屹然

1. 重慶人文科技學院 工商學院，重慶 合川 401524；2. 重慶科技學院 法政與經貿學院，重慶 401331

經濟繁榮和技術進步推動科技不斷創新, 同時科技創新又反過來驅動經濟快速發展[1-3]． 為了促進科技項目的有效管理, 規范科技項目的投資與實施, 建立科學、 可信的科技項目評估制度十分必要[4-6]． 趙玲等[7]為了推進金融與科技的有機結合, 將層次分析法(Analytic Hierarchy Process, AHP)與數據包絡分析法(Data Envelopment Analysis, DEA)進行融合, 提出了針對杭州科技金融績效分析的AHP-DEA法． Kim等[8]通過制定一個建筑物及拆除廢物管理績效評估框架, 綜合保證了利益相關者的相關權益． 王宗軍等[9]針對煙草行業商業系統相關的項目績效分析問題, 通過在3E原則基礎上對湖北省煙草項目進行分析, 并在AHP和熵權法的基礎上構建了科技項目績效評估體系． 本文在隨機層次分析法( Stochastic Analytic Hierarchy Process, SAHP)與云模型等理論基礎上, 構建了SAHP-云模型評估方法, 旨在提升科技投入項目績效評估的合理性與科學性． 由于當前的項目績效評估方法存在主觀性與隨機性較強的缺陷, 因此本文提出的綜合評價方法理論上解決了評估隨機性的問題, 具備一定的創新性, 同時在實際應用上本文的綜合評價方法相較于以往的研究簡化了評估過程, 并在遵循隨機性的同時保證了結果的真實性．

1 基于SAHP-云模型的科技投入項目績效評估方法研究

1.1 基于SAHP-信息敏感性的科技投入項目績效評估指標體系建構

為了提升科技投入項目績效評估的合理性, 本文在SAHP與云模型等理論基礎上, 構建了科技投入項目績效評估方法, 并對其實際應用效果進行了分析． 科技投入項目績效評估方法的構建, 首先需要對其評價指標體系進行構建． 其具體步驟如圖1所示．

圖1 評價指標體系構建流程

從圖1中可以看出: ① 構建流程首先是收集信息資料, 此時同步收集相應的指標; ② 分析評價目標; ③ 選擇指標體系與類別, 同時確定指標設計原則; ④ 初選指標; ⑤ 二次篩選指標, ⑥ 確定指標權重; ⑦ 構成指標體系． 在確定指標體系權重時, 本研究為了減少指標的冗余度, 降低專家評估的工作量, 選擇了信息敏感性理論來確定指標的客觀權重, 同時還充分考慮專家進行評價時的隨機性, 選擇了SAHP來確定指標的主觀權重． SAHP綜合運用層次分析法與隨機變量方法, 同時綜合考慮了人在做出決定時的不確定因素, 其核心是把初始判別矩陣中的常量轉換成隨機變量, 以此獲得不同的隨機矩陣[10-12]．

利用SAHP計算主觀權重首先需要建立層次結構模型; 其次就是構建判斷矩陣． 假定層次結構模型某個層次內存在多個指標, 此時邀請專家根據1～9的標度法對多個指標進行指標間比較, 得到的判斷矩陣如式(1)所示．

(1)

式(1)中,D表示判斷矩陣;dij為該矩陣中的元素, 表示兩個指標相比后的重要程度;n表示指標的個數;i和j表示序號不等的指標． 在確定矩陣中元素的具體值時, 可以根據不確定情況來自由選擇精確值、 區間值或三角形模糊數的評分格式, 從而較好地解決了專家評定行為的模糊性問題． 在得到判斷矩陣后, 可以將其轉化為隨機判斷矩陣, 此過程利用貝塔分布方法將評價值轉換為隨機變量; 然后將隨機變量轉化為精確值; 接著開始一致性檢驗; 最后對單個專家評價的指標權重進行計算, 這一步采用算術平均方法[13-15]． 值得注意的是, 將判斷矩陣轉換為隨機判斷矩陣及將隨機變量轉換為精確值的兩個步驟有別于傳統層次分析法的步驟, 專家能給出區間值和三角形模糊數的評分, 從而減少了評估困難, 避免損失有效信息, 并用適當的隨機變量表達了評估值, 使評估結果不受精確值約束． 判斷矩陣內所有的元素均以實數表示, 之后的步驟與傳統層次分析法相同．

利用算數平均方法對各專家的判斷矩陣進行加權運算, 求出該層次中各指標與高層指標之間的權重, 其計算公式如式(2)所示．

(2)

(3)

式(3)中,ωk表示最終的主觀權重,λk表示專家k的權重． 在確定主觀權重后, 可以利用信息敏感性理論確定客觀權重[16-18], 相應的計算公式如式(4)所示．

(4)

(5)

圖2 指標評價體系具體內容

從圖2中可以看出, 4個1級指標分別為相關人員滿意程度(A)、 直接經濟效益(B)、 間接經濟效益(C)及目標實現狀況(D)． A指標下分別為顧客、 投資主體及領導滿意程度; B指標下分別為投入與產出比率、 萬元支出新增加的銷售額度、 萬元支出新增加的產量、 萬元支出新增加的利潤值、 萬元支出費用減少; C指標下分別為萬元新設科研院所數目、 萬元支出科技相關活動人員數量、 萬元支出新增就業人數、 萬元支出重大成果總數; D指標下分別為目標完成比率、 目標完成質量、 工程完工及時性、 工程驗收有效性．

1.2 基于云模型的科技投入項目績效評估流程分析

在SAHP確定主觀權重、 信息敏感性理論確定客觀權重的基礎上構建完成指標體系后, 需要選用相關評價方法對其進行評價． 本研究綜合考慮后選擇云模型與專家評價法對其進行評價, 根據構建完成的指標體系制定的績效評估實施流程如圖3所示．

圖3 科技投入項目績效評估實施流程圖

從圖3中可以看出, 績效評估實施流程總共分為6步; ① 針對特定的被評估項目, 利用內容和專家精確性的推薦方法從專家數據庫中選出最適合的專家; ② 按照指標體系設計出科學工程業績評估表; ③ 根據專家評估結果, 建立一個初始評估矩陣, 并根據該模型的偏好表達式, 把評估矩陣轉換為“云”矩陣; ④ 利用云模型對評估中出現的異常進行識別校正, 得出“云”矩陣; ⑤ 根據專家的初步評估矩陣來確定各專家的權重; ⑥ 利用云模型中的虛擬云產生算法, 從下到上收集評估信息, 并用“浮動云”來表示各標準層面的評估資料, 將“浮動云”集中在各個標準層, 形成一個代表項目最終評估結果的“綜合云”． 在績效評估流程中, 本研究在云模型的基礎上優化了傳統的模糊綜合評價方法, 將模糊與隨機相結合, 避免專家評價的主觀、 隨意性, 從而提高了評價的精確性． 其具體內容如圖4所示．

圖4 利用云模型優化模糊綜合評價的具體內容

從圖4中可知, 具體內容包含偏好表達、 識別異常數據、 確定專家權重、 評估信息匯總． 云模型偏好表達中比較重要的就是熵值(En)、 超熵值(He)、 期望值(Ex)． 原始He和En代表了評估結果的隨機與模糊性． 另外, 傳統的專家評價法受主觀行為影響比較大, 從而會造成評估結果可靠性大幅度降低． 為了避免個別異常數據對整個評估結果造成不必要的影響, 需要對這些異常數據進行識別． 其評估結果矩陣如式(6)所示．

(6)

式(6)中,S表示評估結果矩陣,m′表示專家的個數,n表示評估指標的個數;s表示矩陣內部元素． 由于評估指標已經轉化為云形式, 因此將評估指標結果異常數據設置為Sij=(Ex1,En1,He1)． 依據云模型的修正原則, 異常數據的修正表達式如式(7)所示．

(7)

(8)

(9)

科技投入項目績效評估關乎知識產權密集型產業升級． 在知識產權密集產品中其接近度與產業升級的可能性之間存在正相關． 同時, 其動態演技以臨近性升級為主, 跳躍性升級為輔． 以中國為例, 知識產權密集產品的臨近效應可以起到推動作用． 另外, 知識產權密集型產品的鄰近能力累積, 能夠降低其所需能力水平, 增加對產業升級的負向影響．

2 基于SAHP-云模型的科技投入項目績效評估方法效果研究

為了驗證SAHP-云模型的有效性, 本研究在相關科技項目網站上隨機邀請10位相關專家作為評審小組成員, 對相應指標之間的重要性做出判斷． 此過程首先依據專家知識體系和工作經驗進行必要的篩選, 并在篩選完成后的專家群體中利用隨機法來邀請, 這樣既保證了專家可信度下限, 也可以充分發揮SAHP的隨機性優勢． 本研究選擇的科技投入項目信息為“科學基金共享服務網”中的內容, 在研究開始前需要對權重進行確定, 其結果如圖5所示．

圖5 項目績效評估體系的主客觀權重與綜合權重

在圖5中, 依據信息敏感性理論, 本研究刪除了B3,C1及D1這3個指標, 以此減少信息冗余度． 圖5中3張圖表示項目績效評估體系的主、 客觀權重和綜合權重結果． 從圖5a中可以看出, 評估體系主觀權重B指標值最大, 為0.435． 從圖5b中可以看出, 客觀權重13個指標呈遞減趨勢, A指標下的客觀權重最大, 表明在績效評估中相關人員的滿意程度占較大比例． 從圖5c可以看出, B指標下B4權重值最大, 為0.15, 表明在績效評估中新增利潤占較大比例． 在此基礎上, 本研究依據百分制原則, 利用云模型將評價等級劃分為5個標準:S-2(0-40),S-1(40-60),S0(60-75),S1(75-90),S2(90-100)．

依據云模型優化的模糊綜合評價內容, 本研究首先對云模型偏好表達進行了實驗驗證． 由于篇幅受限, 只用A指標下專家原始評估數據云模型表示． 另外, 本研究還運用云圖對A1指標進行評估, 其結果如圖6所示．

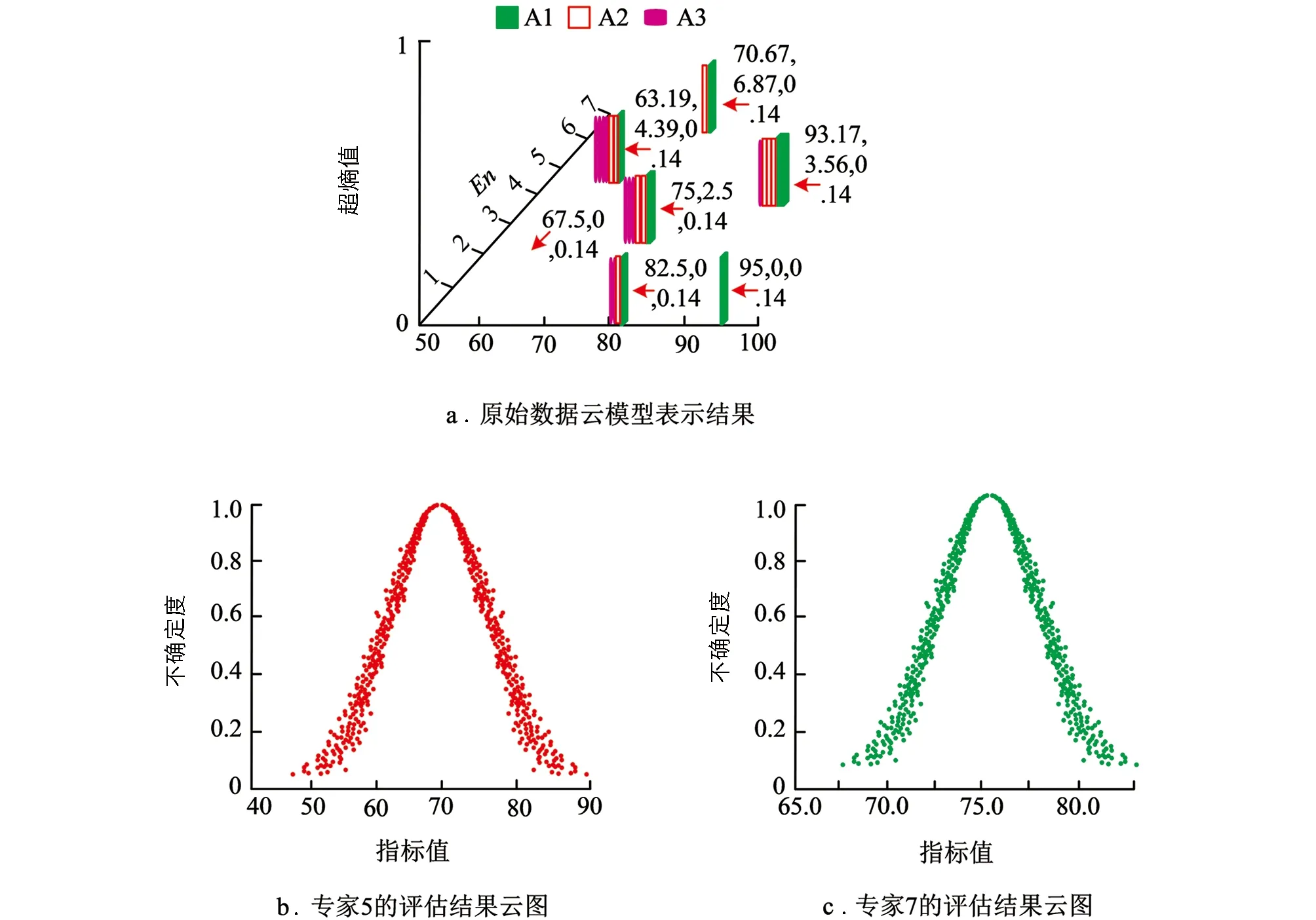
圖6 A指標下專家原始評估數據云模型表示結果

從圖6中可以看出, 專家評估結果的期望評分大致維持在63～94分之間． 另外, 從兩個專家對A1指標的評估結果來看, 專家5的橫軸以10為單位, 明顯比專家7的寬泛度更高, 表明專家5的評估結果不確定性更高． 綜合來看, 云模型可以比較科學地表示專家的評估結果． 同時, 云模型的En值和He值也充分體現了專家評價的隨機性． 在此基礎上, 本研究利用云模型來確定專家權重, 依據專家的不確定度與偏差度來計算, 其結果如圖7所示．

圖7 專家權重確定的結果

從圖7中可以看出, 專家2的不確定度和專家6的偏離度最大, 分別為15和174, 表明兩位專家存在個人經驗、 對項目缺乏了解及意見不符等問題． 將專家不確定度和偏差度賦值為0.5后, 得到的專家權重維持在0.08～0.14之間． 其中, 專家10的權重最大, 為0.14． 在專家權重給出后, 本研究有效集結了專家和1,2級指標的信息, 計算出浮動云, 其結果如表1所示．

表1 集結專家和1,2級指標浮動云

從表1中可以看出, B4指標即萬元支出新增加的利潤期望值最大, 為89.75; D3指標的熵值最小, 為0.71, 說明10位專家在該指標上的看法較為一致, 而A2指標和A3指標的熵值為2.82和2.81, 數值最大, 表明10位專家在兩個指標上分歧最大, 因此其模糊性與隨機性最大． 在1級指標中, D指標的熵值最小, 看法最為一致; A指標的熵值最大, 隨機性最大, 得分穩定性較低． 綜合來看, 該科技投入項目的期望值為81.12分, 超熵值為0.12, 處于較低水平, 表明專家組對該項目的評估結果較為一致, 同時也表明SAHP-云模型方法在該科技投入項目績效評估中降低了評分的模糊性和隨機性, 提升了評估結果的科學性與合理性．

3 結論

針對當前項目績效評估主觀性強、 合理性較低的問題, 本研究引入SAHP和云模型理論, 構建了SAHP-云模型評價方法, 并將其應用于實際的科技投入項目, 在云模型表示、 專家權重確定及雙指標層3個方面實驗的基礎上, 驗證其有效性． 實驗結果表明, 從云模型表示結果來看, 單論A1指標專家5比專家7寬泛度更高, 符合原始數據云模型表示結果． 從專家權重確定結果來看, 專家權重維持在0.08～0.14之間, 其中專家10的權重最大, 為0.14． 從專家與2級指標信息集合結果來看, 1級指標中D指標熵值最小, 為0.92, A指標熵值最大, 為2.76, 而綜合云結果超熵值為0.12, 處于較低水平． 綜合來看, 本研究給出的SAHP-云模型方法在科技投入項目績效評估上基本符合原始專家評估結果, 同時也降低了專家評估中的模糊性和隨機性, 從而具備較強的科學性和合理性． 值得注意的是, 本研究采用的虛擬云在指標信息集結上還需要更深一步探討, 從而構建出更完善的數據處理方法．