基于相空間重構與GSA-LVQ的有載調壓變壓器分接開關機械故障診斷
趙書濤,李小雙,李大雙,徐曉會,李云鵬,李波
(華北電力大學 電子與電氣工程學院,河北 保定 071003)
0 引 言
隨著電網的快速發展以及國民對電能質量的要求提高,有載調壓電力變壓器得到越來越廣泛的應用,在電力系統中起著調節潮流和穩定負荷電壓的作用。有載調壓變壓器通過其唯一可動部件分接開關(OLTC)來實現調節功能,隨著調節的次數增多,OLTC故障的幾率就會增加。據國內外資料顯示,機械故障是有載調壓變壓器的主要故障類型[1],這不僅會損壞分接開關和變壓器,還會影響電力系統正常運行。對OLTC進行在線監測與故障診斷,就能夠及時發現潛在故障,對電力系統安全運行具有重大意義。
OLTC在線監測和故障診斷技術起步于20世紀90年代,其中最常見的是記錄傳感裝置采集到的機械振動信號、驅動電機電流信號,通過進行信號處理提取信號的時域、頻域特征,從而判斷OLTC的機械狀態[1-2]。從振動信號中提取設備狀態特征的方法很多,常見的振動信號分析方法有小波變換、包絡線法、經驗模態分解等[3-4]。以上時、頻域方法的分析具有一定的局限性[5],只能提取少量的有效信息,研究發現,OLTC振動結構本身是一個非常復雜的非線性動力學系統,且振動信號表現出混沌特性,混沌診斷理論能夠很好地分析OLTC的振動信息。目前,混沌理論被逐步應用于電力系統中電纜、配電網和滾動軸承等設備的故障診斷問題[6-8],但在有載調壓變壓器分接開關故障診斷領域的應用極少。LVQ神經網絡是一種優良的分類器,具有較強的適應能力,得到了廣泛的應用。但網絡中存在嚴重的初始連接權值敏感問題[9]。
提出一種基于相空間重構-GSA優化LVQ的有載分接開關機械故障診斷方法。根據OLTC振動信號動力學特征,對振動信號進行CEEMD分解,得到一組IMF分量,并通過C-C法計算嵌入維數和延遲時間重構相空間,計算李雅普諾夫指數和關聯維數形成向量進行特征描述,通過GSA算法[10]優化LVQ神經網絡,解決輸出層與競爭層之間連接權值選擇困難導致診斷率低的問題,構建GSA-LVQ分類器實現OLTC機械狀態識別。
1 利用CEEMD構造一維時間序列
振動信號包含OLTC切換過程中大量機械狀態信息。通過模擬浸油式CM型OLTC的三種運行狀態(正常切換、開關滑檔、電機機構故障),利用粘合于有載分接開關頭蓋處的YD-37壓電式加速度傳感器結合PCT8192采集卡進行數據采集,由GD201信號電纜傳輸至微型計算機進行數據處理以及狀態識別。每種運行狀態采集了40組數據,OLTC三種振動信號時域波形如圖1所示。
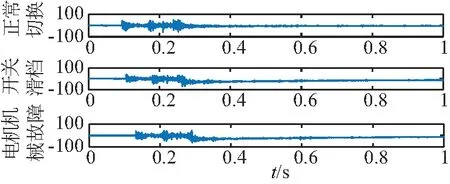
圖1 三種振動信號
CEEMD是Yeh等[11]在EMD和總體平均經驗模態分解(EEMD)[12-13]上優化的基礎上提出了的一種信號時頻域分析方法。解決了EMD方法嚴重的模態混疊現象,同時也克服了EEMD因添加單個白噪聲帶來的重構誤差問題。具體的分解步驟如下:
(1)將一對白噪聲分別添加到原始三種振動信號(正常切換、開關滑檔、電機機構故障)。為了提取OLTC振動信號的特征,使用CEEMD對原始振動信號Xi(t)添加成對的白噪聲mi(t),得到兩種不同的新信號Pi(t)和Ni(t)。
Pi=x(t)+mi(t)
(1)
Ni=x(t)-mi(t)
(2)
(2)對這兩種不同的新信號分別進行EMD分解,得到j個IMF分量cj(t)=d。
(3)
(3)重復上述步驟,每次加入新的正態分布白噪聲序列,并將每次得到的IMF作為最終結果。
以正常切換振動信號為例,對其進行CEEMD分解,得到6階不同特征尺度的IMF分量,每階本征模態分量是振動信號分解后按照頻率排列,包含了振動信息不同時間特征尺度大小的成分,能夠將機械系統中的混沌系統信息蘊含在其中,如圖2所示。
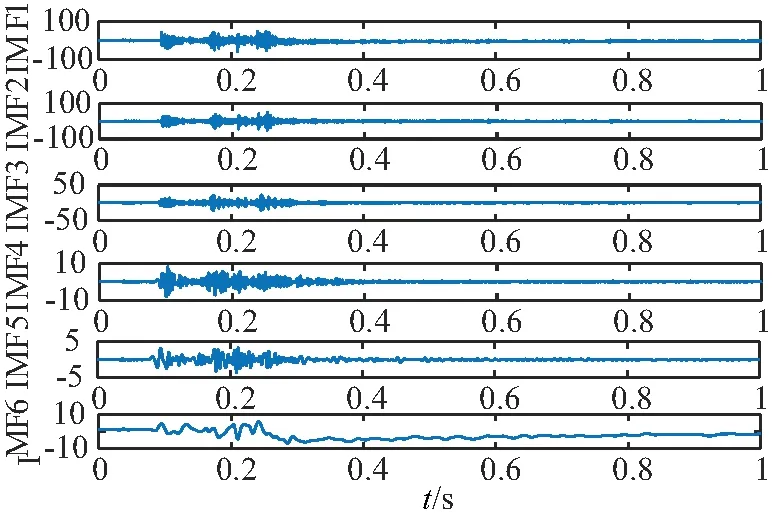
圖2 不同頻率振動信號的CEEMD分解
2 相空間重構的理論與方法
2.1 重構相空間
在OLTC這個非線性振動系統操動過程中,相空間重構能夠保持原非線性動力系統的幾何不變性[14],采集到的振動信號表現為振動幅值隨時間的演變序列,單變量的時間序列中隱含著設備的狀態信息,該序列是分析OLTC特征的重要信息源。經CEEMD分解得到的固有模態函數序列是在時間域上的序列,相空間重構就是對混沌時間序列進行處理,從時間序列中提取到更多OLTC的狀態信息。文中應用延遲坐標法[15],選取任意一個IMF分量時間序列{Yi(t)}經不同延時構造狀態向量,重構相空間可由式(6)表示:
(4)
x(k)=x(t+kΔt),k=1,2,…N
(5)
(6)
式中x(k)為k時刻離散化的系統值;τ為延遲時間;m為嵌入維數;t為采樣開始時刻;Δt為采樣間隔;N為采樣長度。
重構相空間的過程中尤為重要的是選取延遲時間和嵌入維數這兩個參數。
2.2 確定延遲時間和嵌入維數
在前人研究的基礎之上,文中認為二者是相關聯的[16-17],并采用C-C算法對延遲時間和嵌入維數進行聯合計算,和其他算法相比,此算法融合了自相關和互相關算法的優點,計算量小、操作容易易實現,在求解分線性模型方面有著較大優勢[18],計算步驟如下:
(1)根據延遲時間τ的不同,將振動信號的每階固有模態分量序列{Yi(t)}劃分為τ個不相交的時間序列S(m,N,r,τ)。
(7)
(8)
M=N-(m-1)τ
(9)
(10)
(11)
式中dij為∞函數;r為搜索半徑,取小于max(dij)的任意值;θ(x)為Heaviside函數;C(m,N,r,τ)為嵌入時間序列的關聯積分;
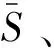
(12)
(13)
(14)
(15)
式中nm為m個可能的取值;nk為k個可能的取值。
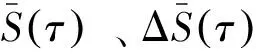
(16)
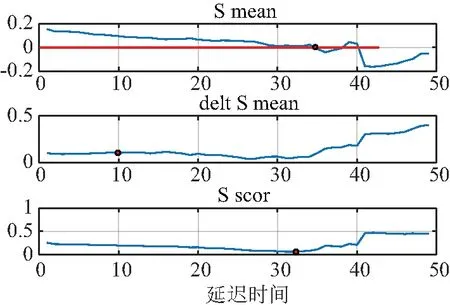
圖3 OLTC固有模態分量序列的S mean曲線、delt S mean曲線和S scor曲線
因重構相空間的冗余和奇異吸引子軌道擁擠程度會因這兩個重要參數的改變而改變,所以C-C算法得到的延遲時間和嵌入維數即為最優值。
3 混沌運動的特征提取
在實際工程應用中,存在潛在故障的OLTC振動信號會因時域、頻域分解長度不同而存在波形相似的情況,而且相空間直觀圖并不能定量反映非線性系統的本質特征,重構向量空間后需要度量其動力學特性,因此需要引入最大李雅普諾夫指數和關聯系數進行特征描述。
關聯維數D是判斷序列是否具有混沌特性的關鍵指標。通常由飽和關聯維數法(G-P法)進行計算,當鄰域半徑r趨于零時,所求極限即為關聯維數,計算公式如下:
(17)
(18)
(19)
下面以正常切換為例,通過G-P算法[19]求解OLTC固有模態分量序列的關聯維數,lnC-lnr曲線關系如圖4所示,擬合m=4時所得直線斜率為0.036 6,可認為OLTC振動信號固有模態分量的關聯維數D=0.036 6。
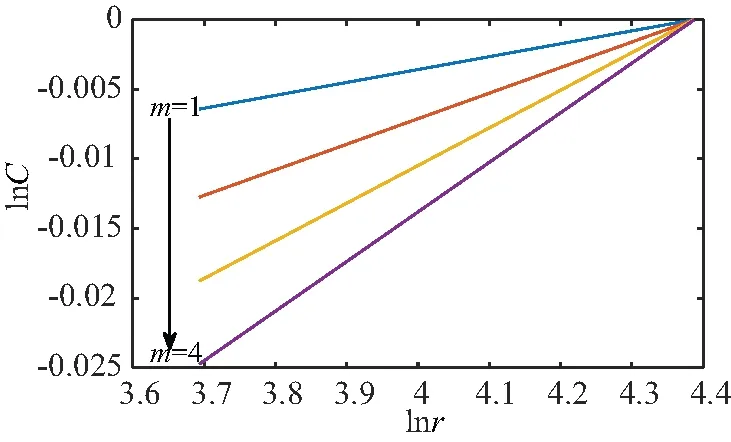
圖4 OLTC固有模態分量序列的lnC-lnr曲線
李雅普諾夫指數是用來評價系統的收斂或發散程度的指數。其中最為經典的是Wolf提出的一種求最大李雅普諾夫指數的方法,計算步驟如下:
(1)利用相空間重構技術,對采樣點為N的樣本序列構造m維相空間新序列, 見式(16);
(2)尋找與初始相點距離最近的點P0(t0),并跟蹤測量兩點間的距離L0是否大于ε。
L0=|P(t1)-P0(t1)|>ε
(20)
(3)尋找一點與P0(t0)相間夾角最小且距離最近的一點。
L′1=|P(t1)-P1(t1)|<ε
(21)
(4)重復上述步驟,直至迭代所有的序列點,最大李雅普諾夫λ計算公式如下:
(22)
式中T為迭代次數。
根據Wolf提出的求解最大李雅普諾夫指數的方法中式(20)~式(22)可計算相空間的最大李雅普諾夫指數。表1是以正常切換狀態下振動信號為例的特征向量:最大李雅普諾夫指數和關聯維數。
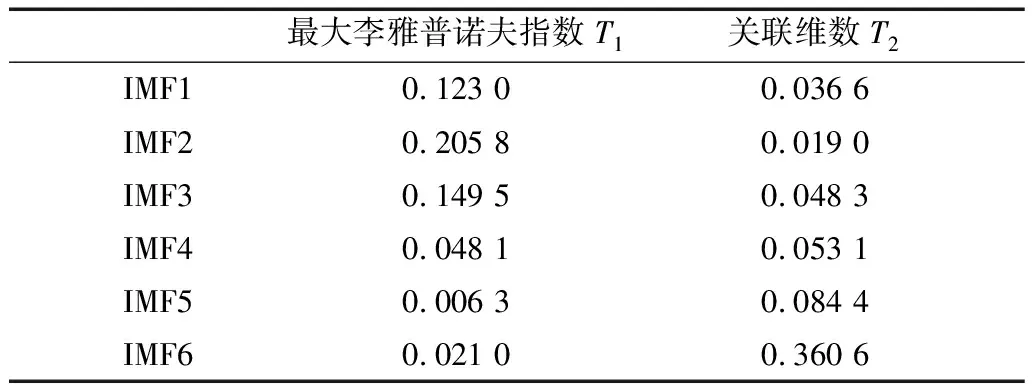
表1 重構相空間特征
兩個指數在混沌力學角度上一定程度地描述了OLTC所有相點在相空間內的分布特性,可將二者提取出來作為重構相空間分布特征T1=[T11,T12,…,T16]和T2=[T21,T22,…,T26]。
將OLTC每種運行狀態對應的12維特征量T=[T1,T2]=[T11,T12,…,T16,T21,T22,…,T26]輸入神經網絡中進行機械狀態識別。
4 基于GSA優化的LVQ有載分接開關機械故障診斷
4.1 GSA優化LVQ算法
LVQ神經網絡是用于分類的監督學習算法,同時融合了競爭學習特點,是一種最近鄰原型分類器。它由輸入層、競爭層和線性輸入這三層神經元構成[20],結構如圖5所示。LVQ存在初始權值敏感問題,當初始權值偏差過大,不僅會導致資源浪費,同時較大程度上影響網絡的診斷速度和識別效果。
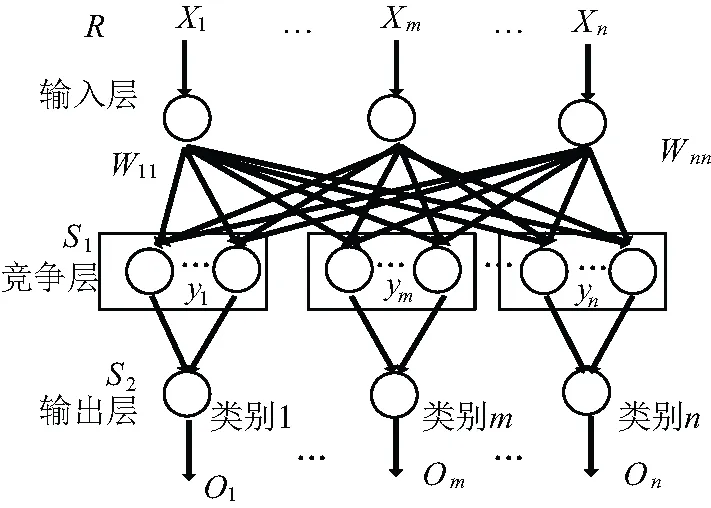
圖5 LVQ網絡結構示意圖
采用全局搜索能力較強的GSA算法對LVQ的競爭層網絡權值wii(12×16個權值向量)進行全局尋優。將粒子編碼賦給網絡權值,通過牛頓第二定律進行迭代,尋找粒子的最優位置。構造一個輸入R=12維特征,輸出S2=3維二值向量的LVQ網絡,在訓練過程中通過GSA算法對粒子適應度的不斷更新,實現對LVQ網絡初始權值的不斷調整。
LVQ網絡權值優化過程具體如下:
(1)創建LVQ網絡,初始化網絡權值wij,形成n個隨機初始化粒子位置編碼。
(23)
(2)計算初始粒子適應度,采用均方誤差最小作為萬有引力算法尋優的適應度函數。
(24)
式中N為樣本數;wj為實際輸出值;wi為期望值。
(3)計算t時刻粒子j對i的萬有引力。
(25)
(26)
(27)
(28)
(29)
(30)
式中randj為0~1之間的隨機數。
(5)判斷循環是否終止。當迭代次數大于設定最大迭代次數,則尋優終止,反之,返回步驟(2)。
(6)按照上述步驟,訓練模型已經生成,接下來可將測試數據輸入模型即可完成狀態診斷。
4.2 有載分接開關故障診斷
采用GSA-LVQ的有載分接開關診斷流程圖如圖 6所示。
將90組用于網絡訓練,30組用于測試診斷算法正確率,基于GSA-LVQ的OLTC故障診斷結果如圖7所示,圖中縱坐標的數字對應OLTC三種機械狀態(1:正常切換;2:開關滑檔;3:電機機構故障)。由診斷結果可知GSA-LVQ根據描述動力系統特征量進行狀態識別的正確率達96.6667%,可靠性較好。對比GSA-LVQ與LVQ算法診斷結果如表2所示,相比之下優化后的算法大大縮短了尋優時間,診斷正確率有所提高,說明提出的GSA-LVQ是有效的,可在一定程度上彌補LVQ對初始權值敏感的缺陷。

表2 不同算法診斷時間和分類準確率
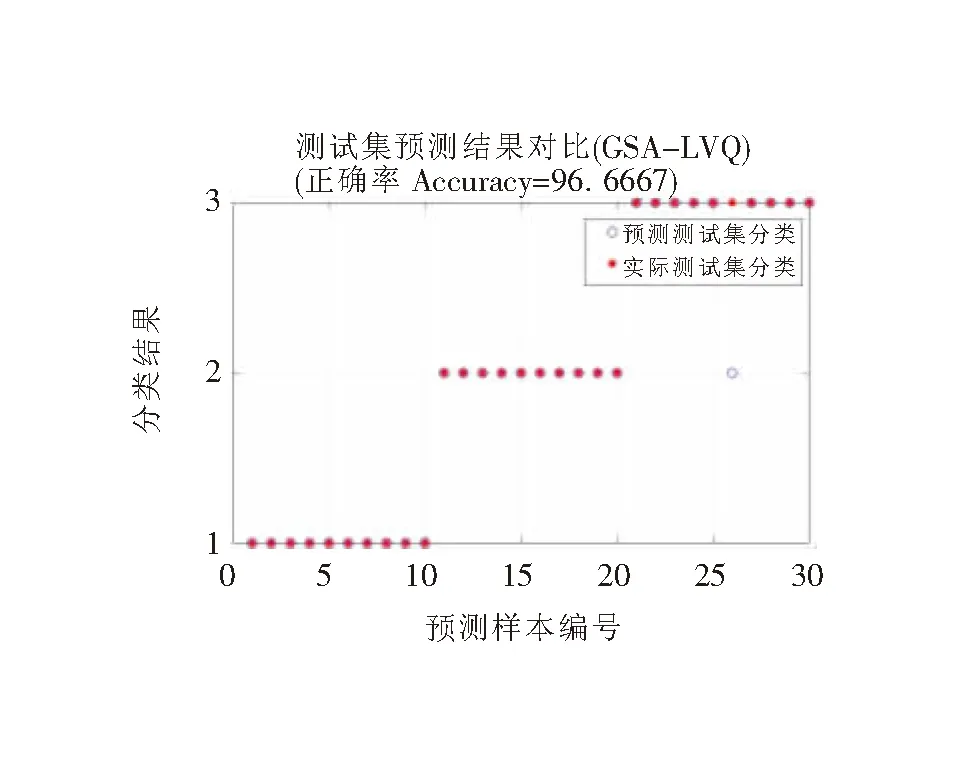
圖7 GSA-LVQ神經網絡診斷結果
5 結束語
提出基于CEEMD、相空間重構和GSA-LVQ的有載分接開關的振動信號分析及機械故障狀態識別算法,檢測OLTC機械故障準確率較高。通過CEEMD分析得到的IMFs分量,從混沌動力學分析角度引入重構相空間,彌補了傳統時頻域方法分析OLTC振動信號的缺陷;實驗證明,由GSA優化LVQ神經網絡算法在診斷時間、準確率方面都有所提升,一定程度上克服了自身對初始權值敏感的問題,增強了學習效率和網絡性能。

