基于機器學習的殷墟花園莊M54青銅器p-XRF成分數據再思考

黃 希,楊清越,何毓靈

(中國社會科學院 考古研究所,北京 100102)

引言

安陽殷墟花園莊東地 M54(1)中國社會科學院考古研究所:《安陽殷墟花園莊東地商代墓葬》,科學出版社, 2007年,第227頁、第251-252頁。位于安陽殷墟宮殿宗廟區內,整體保存完好未經盜擾,年代屬殷墟文化二期偏晚階段,其絕對年代相當于祖庚、祖甲時期,隨葬品精美豐富,對研究殷墟時期的墓葬制度、軍隊體制、手工業發展等問題具有重要意義。

M54出土青銅器200余件,包括禮器、兵器和生產工具等,形制獨特,紋飾精美,制作工藝高超,被譽為中國青銅器制作技術的巔峰之作之一。殷墟青銅器的發現對于研究中國古代社會和文明、青銅器制作技術和思想文化等方面都有著重要的意義。劉煜等(2)劉煜、何毓靈、徐廣德:《M54及M60出土青銅器的成分分析》,《安陽殷墟花園莊東地商代墓葬》,科學出版社, 2007年,第289-296頁;劉煜、賈瑩、成小林、姚青芳:《M54出土青銅器的金相分析》,《安陽殷墟花園莊東地商代墓葬》,科學出版社, 2007年,第297-301頁。對M54出土青銅器化學成分及金相組織結構等進行研究,主要采用高錫的銅錫二元合金,兵器錫含量低于禮器,大部分器物鉛含量低于2%,為原料中雜質帶入,少部分紋飾精細、器型復雜的禮器(如牛尊、方尊等)鉛含量較高,體現出工匠對合金配比與性能之間的關系已經有了充分的認識。

對于青銅器制作技術及腐蝕問題的研究涉及到大量成分數據信息,隨著檢測設備的普及與檢測精度的提升,成分分析檢測的操作門檻已經大幅降低,越來越多的考古單位配備了以便攜式X射線熒光能譜儀(p-XRF)等為代表的便攜式分析檢測設備,在考古一線即可獲取大量的成分分析數據。以往單一目的、單一處理方式的數據研究模式已無法滿足精細化考古工作現場對于大規模數據深入分析的要求,目前在處理、識別并分析這些數據背后代表的文物信息、歷史信息方面還存在很大欠缺,存在成分分析數據存量急速增加但研究利用率低的問題。基于當下在信息技術領域爆發式發展的機器學習技術,通過機器學習的數據挖掘和模式識別功能,使用現存數據進行聚類、分類、關聯規則挖掘等識別出有用的模式和信息,或根據已知特征和模式來識別新的實例數據,對于在考古一線根據大規模的分析監測數據快速識別、量化、區分文物本體材料特征以及可能存在腐蝕病害具有重要的應用價值。

一、機器學習

1.1 機器學習概述

機器學習是一種人工智能技術,通過使用算法和統計模型讓計算機模擬人類的學習行為,在不進行明確編程的情況下自動識別和理解已知數據的模式,從數據中自動學習并提高算法性能,找到規律并用于數據預測、分類、聚類等相關任務(3)劉霏凝、石競琛、王文杰、趙瑞:《材料科學中機器學習算法的應用綜述》,《化工新型材料》2022年第9期。。這種學習過程不需要明確的程序指示,而是借助于大量的數據和統計學方法來確定關系和模式(4)Ceriotti M:《Atomistic machine learning between predictions and understanding》,《Journal of Chemical Physics》2019年第15期。。機器學習主要包括以下幾個個步驟(5)劉悅、鄒欣欣、楊正偉、施思齊:《材料領域知識嵌入的機器學習》,《硅酸鹽學報》 2022年第3期; Jing L、Tian Y:《Self-Supervised Visual Feature Learning With Deep Neural Networks: A Survey》,《IEEE》2021年第11期;G. Ruschioni、 D. Malchiodi,、A.M. Zanaboni、 L. Bonizzoni,Supervised:《Supervised learning algorithms as a tool for archaeology: Classification of ceramic samples described by chemical element concentrations》,《Journal of Archaeological Science: Reports》2023年第49期。:數據預處理、模型構建與訓練以及模型評估,根據不同的任務選擇適合的模型,并通過大量的數據對其進行訓練,最終得到一個可以準確預測未知數據的模型。

機器學習可以按照學習方式和使用的數據集分成三類:監督學習、無監督學習、和強化學習。本研究主要用到監督學習和無監督學習兩種形式。

監督學習(supervised learning)是一種利用有標記的訓練數據來進行模型訓練和預測的機器學習方法。在監督學習中,需要將輸入數據和對應的輸出標記作為訓練數據來訓練模型,建立輸入和輸出之間的映射關系,使得模型能夠根據輸入預測出正確的輸出。常見的監督學習算法包括:回歸分析、決策樹、支持向量機、神經網絡和樸素貝葉斯算法等。

無監督學習(unsupervised learning)是一種不需要標記或僅少量標記的訓練數據,直接從數據中尋找數據集中的特征和模式的方法。在無監督學習中,只需要將輸入數據作為訓練數據來訓練模型,模型會自動學習輸入數據的內在結構和規律,并基于此對未知數據進行預測和分類。常見的無監督學習算法包括:聚類分析、降維分析和關聯規則挖掘等。

監督學習、無監督學習各有特點和優勢(6)Meng T、 Huang R、 Lu Y:《Highly sensitive Terahertz non-destructive testing technology for stone relics deterioration prediction using SVM-based machine learning models》,《Heritage Science》2021年第9期;王祉皓、趙薌溦、智群、郭明:《基于機器學習的風化硅酸鹽玻璃原成分預測及亞分類方法》,《硅酸鹽學報》2023年第2期。,在本研究中,主要使用監督學習和無監督學習方法,具體包括監督學習中的支持向量回歸算法SVR,以及無監督學習的K均值聚類算法K-means和層次聚類算法。在研究過程中,還嘗試使用線性回歸(Linear Regression)算法、K 最近鄰回歸(K-Nearest Neighbor Regression,KNN回歸)算法、梯度提升決策樹(XGBoost)算法、隨機森林(Random Forest)(7)李欣海:《隨機森林模型在分類與回歸分析中的應用》,《應用昆蟲學報,》2013年第4期;Qianqian H、Wei L、Siran L、Jianli C:《Detecting? copper trihydroxychloride with reflectance spectroscopy and machine learning methods》,《Journal of Cultural Heritage》2023年總第59期;Jones C、 Daly N S、 Higgitt C: 《Neural network-based classification of X-ray fluorescence spectra of artists' pigments: an approach leveraging a synthetic dataset created using the fundamental parameters method》,《Heritage Science》2022年第10期。算法等方法。

1.2 SVR支持向量回歸算法

支持向量回歸算法(Support Vector Regression)(8)王定成、方廷健、唐毅等:《支持向量機回歸理論與控制的綜述》,《模式識別與人工智能》2003年第2期。是一種基于支持向量機的非線性回歸算法,用于解決連續型數據預測問題。SVR通過選擇核函數將原始的高維特征空間映射到低維空間中進行分類和回歸,找到一個能夠最大化邊界(函數間隔)和限制條件之間的平衡點的超平面模型,以建立輸入變量(特征)和輸出變量之間的映射關系,進而對新樣本進行分類和預測。

1.3 K-means K均值聚類算法

K均值聚類算法(K-means Clustering)(9)陶瑩、楊鋒、劉洋等:《K均值聚類算法的研究與優化》,《計算機技術與發展》2018年第6期。是一種基于距離度量的無監督學習方法,它將數據集中的樣本按照相似度進行分組,形成k個簇。該算法首先隨機指定k個中心點,然后計算每個樣本與中心點的距離,并將其分配給距離最近的中心點所在的簇。接著,重新計算每個簇的平均值或中心點,并將新的中心點作為該簇的代表。反復迭代上述過程,直到簇內所有樣本都與其所在簇的中心點的距離最小。

1.4 HCA層次聚類算法

層次聚類算法(Hierarchical clustering)(10)賈瑞玉、李振:《基于最小生成樹的層次K-means聚類算法》,《微電子學與計算機》2016年第3期。是一種基于計算數據點之間的相似度量的無監督學習方法,它將相似性(或距離)作為度量,計算每個樣本之間的距離,然后將相似度高的數據點依次進行合并,通過慢慢合并最接近的簇,依次形成一個層次化的劃分為不同群集(cluster)的聚類圖。相似性度量指衡量數據點間相似程度的方法,包括距離、相似性系數、相關系數等,可基于歐氏距離、曼哈頓距離、切比雪夫距離、皮爾遜相關系數等多種距離或相似性手段實現。

二、研究方法

按照一定比例將樣本集隨機分為訓練集和測試集。對屬于訓練集的文物的相關數值化特征與p-XRF中的成分數據組合起來,構成有標簽的樣本集用于訓練模型。使用傳統的文物保護研究工作方法,結合前人研究成果,有針對性地對器物腐蝕成分、器物表面土樣等進行工藝、成分的預研究。根據腐蝕產狀的預研究結果對M54出土銅器的器物類型、腐蝕狀態、腐蝕程度、文物本體穩定性等相關特征進行定性定量的判斷,對每件文物的相關特征分別進行賦值和標記形成樣本集,通過機器學習對成分數據集進行分析,尋找可能存在的數據規律模式,并通過成分數據預測對應樣本所屬的類型。

2.1 腐蝕產狀的預研究

在病害宏觀認知的基礎上,使用常規的文物保護研究方法,包括光學顯微分析(Leica DVM6)、掃描電鏡分析(Phenom XLG2)、拉曼分析(Horiba XploRA、Thermo DXRxi)、X射線衍射分析(Bruker D8 Advance)、離子色譜分析(Thermo ICS-5000)、X射線成像分析(XXQ-2005 型)等,將文物腐蝕產狀和成分、腐蝕產物、保存穩定性等特征相對應,建立對文物特征賦值的標準,對樣本涉及的每件文物特征分別進行數值化,形成有標簽的樣本集,用作訓練機器學習模型。

2.2 機器學習數據獲取與預處理

本研究數據集主要為銅器的X射線便攜熒光能譜儀分析結果,使用Thermo Niton XL3T便攜能譜儀對花園莊M54出土的118件金屬器進行檢測分析,檢測時每個檢測點使用金屬模式檢測,部分采用金屬模式和和礦石銅鋅兩種模式采樣,每個檢測點采集3次,采集時間為30s,取3次讀數的平均值作為一組檢測結果數據進行分析,計量單位為質量比%,對于部分未檢出的化學成分,使用0值進行補全,對于成分比例累加和低于80%的數據組予以剔除。最終得到有效數據280組,其中金屬模式205組,礦石銅鋅模式75組。

2.3 建立機器學習模型

首先明確本次機器學習的目標是對成分數據集進行分類,尋找可能存在的數據規律模式,并通過成分數據預測對應樣本所屬的類型,包括預測器型種類、腐蝕程度及有害性等。

基于以上目的,在前期腐蝕預研究發基礎上,對樣本集的p-XRF數據對應檢測位置的各個特征與數據組分別進行標記形成訓練集,各特征賦值量化標準如下所示:

a.文物類別:容器、兵器、雜器;

b.檢測點腐蝕程度:1致密銹蝕、2疏松銹蝕、3點腐蝕、4有害銹;

c.檢測點腐蝕形態:A鼓起的瘤狀物、B平整片狀銹蝕、C粉末狀銹蝕、D有害銹、E裝飾綠松石、F修復粘接處、G修復焊接處;

從金屬模式中一共有118件銅器,其中兵器35件,容器43件,雜器40件。隨機取42組數據為測試集,其余數據組為訓練集,訓練集包括兵器30件,容器30件,雜器35件,進行機器學習訓練。由于礦石銅鋅模式數據組總數較少,全部用于作分類算法的訓練集。

三、結果與討論

3.1 腐蝕產狀的預研究

在利用文物保護研究技術和手段,對花園莊M54青銅器表面的典型腐蝕產物及分布形態進行檢測分析,建立文物成分特征與腐蝕產狀的判斷標準,為后續對訓練集數據特征進行量化賦值步驟建立標準。

表1 M54銅器典型腐蝕產狀及成分分析

花園莊 M54 青銅器普遍存在殘缺、斷裂、裂隙、變形、層狀堆積、孔洞、表面硬結物、礦化、點腐蝕等多種病害。表面的銹蝕產物主要有孔雀石、赤銅礦、水膽礬、藍銅礦、氯銅礦(11)成小林、楊琴:《五種含氯銅合金腐蝕產物的拉曼光譜及掃描電鏡的分析研究》,《文物保護與考古科學》2018年第4期。、錫石等(12)劉薇、李玲、衛揚波、陳建立:《湖北葉家山墓地出土青銅器的銹層結構研究》,《江漢考古》2019年第4期。主要有孔雀石、藍銅礦、赤銅礦,部分赤銅礦結晶程度較好,呈現大顆粒紫色立方晶狀態,錫石、部,其中分孔雀石與氯銅礦存在形式極為接近,都是淡綠色粉末狀銹蝕。瘤狀物外部及整體大部分為孔雀石,內部靠近青銅基體的部分為赤銅礦。在腐蝕產狀調研過程中,發現部分器物出現特殊的腐蝕現象:1、銅鈴普遍出現嚴重的有害銹病害;2、部分銅容器前期焊接位置出現有害銹病害。

3.2 相關性分析

將器型和銹蝕類型這樣的分類屬性的變量轉化成可以量化的變量后,利用Spearman相關系數計算法得到數據集中元素與元素、元素與器型、元素與腐蝕之間的相關系數,并導出為熱力圖,如圖2、圖3所示。

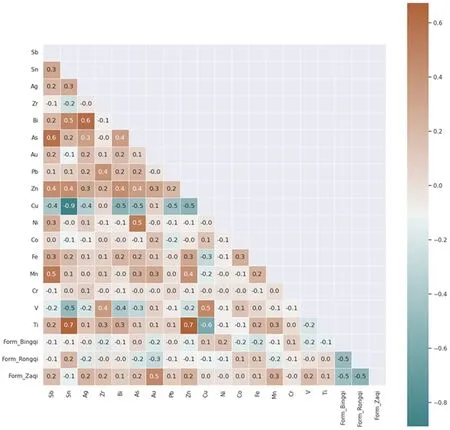
圖2 元素-元素,元素-器類相關性系數熱值圖

圖3 元素-腐蝕狀態相關性系數熱值圖

圖2為元素-元素,元素-器類相關性系數熱值圖,橙色代表正相關,綠色代表負相關,顏色越深代表相關性越強,顏色越淺,代表數值越小。

就元素與元素相關性而言,以Cu元素為例,Cu元素與Sn顯著負相關(-0.9),可能能夠反應出Sn原料是人為單獨加入,類似的還有Cu與Pb的負相關關系。微量元素中,Cu元素與Au(0.1)為正相關,Cu與As(-0.5)、Zn(-0.5)、Fe(-0.3)、Mn(-0.2)等均為負相關;Sn與As(0.2)、Zn(0.4)、Fe(0.2)、Mn(0.1)等均為正相關;Pb與As(0.2)、Zn(0.2)為正相關,Pb與Fe、Mn相關性為0。相關性系數0.1上下的浮動可能并不絕對,但是相關性系數正負性的差別可以視為明顯的區分,銅錫鉛三個主量元素與微量元素相關性系數的正負性差別可能與這些微量元素的不同礦石來源有關。

就元素與器型關系而言。就元素與器型相關性而言,除了符合前期研究中已經發現的Sn元素在容器(相關性0.2)、兵器(相關性-0.1)中的成分差異,Ni、Co、Fe、Cr元素也表現出分別與容器、兵器正負相關的特點,結合可能引入Ni、Co、Fe、Cr等微量元素的礦石來源考慮,古代工匠在不同功能器物冶煉過程中可能存在更多元的合金配比調整。

圖3為元素-腐蝕狀態相關性系數熱值圖,深藍色代表正相關,黃色代表負相關。Level為腐蝕程度,賦值由1-4逐漸加重,腐蝕形態中E裝飾綠松石、F修復粘接處、G修復焊接處為特殊形態,不放入考慮與元素關系。從相關性系數圖中可以看出,腐蝕嚴重程度(Level)與Cl、S元素相關性較大(0.3),C、D腐蝕類型中A鼓起的瘤狀物、B平整片狀銹蝕、C粉末狀銹蝕、D有害銹、E裝飾綠松石,B平整片狀銹蝕與Pb元素相關性較大(0.4),D有害銹與Cl(0.5)、S元素(0.4)相關性極大。

3.3 模型預測結果

在相關性分析的基礎上,分別使用SVR、Linear Regression、KNN回歸算法、XGBoost、Random Forest等算法訓練模型,以金屬模式元素成分與器型關系為訓練集,對測試集中42組元素數據的器型進行預測判斷,并研究模型的精確度。

使用混淆矩陣(13)于營、楊婷婷、楊博雄:《混淆矩陣分類性能評價及Python實現》,《現代計算機》2021年第20期。(Confusion Matrix)來評估模型的性能。比較預測值和真實值之間存在的差異程度。混淆矩陣通常包含四個條目,分別為真正例(True Positive,TP)、假正例(False Positive,FP)、真反例(True Negative,TN)和假反例(False Negative,FN)。

在本研究中,混淆矩陣如表2所示:

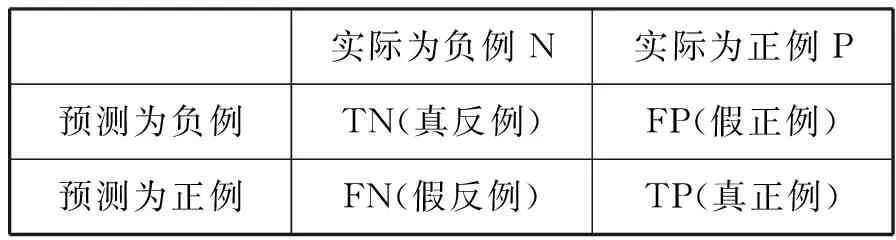
表2 混淆矩陣

其中,TP和TN為預測情況與實際情況相符的正確預測。

預測結果評估圖如圖4所示,預測目標為“判斷元素數據組是否為容器,是為1,否為0”,輸出結果中,橫軸顯示為數據組真實情況,縱軸為模型預測結果,深色塊表示模型預測與現實結果相符,視為準確預測。

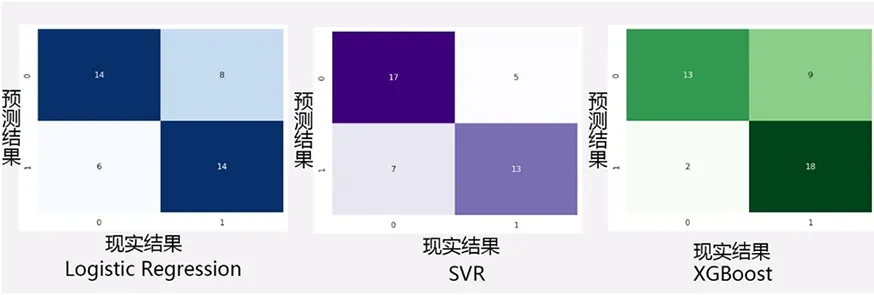
圖4 成分-器型預測結果

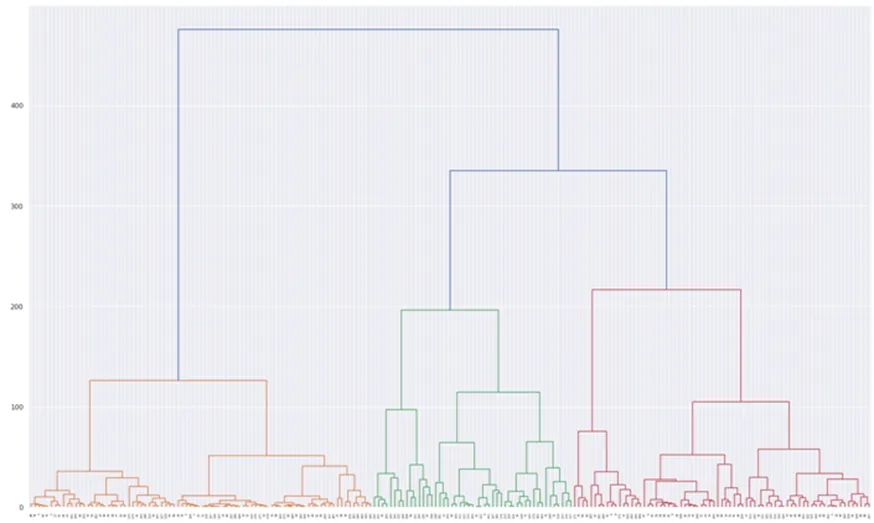
圖5 金屬模式成分HCA聚類分類結果

以SVR預測結果為例,在現實情況為非容器的對應數據組中(橫坐標為0),有17組預測準確,7組預測錯誤;在現實情況為容器的對應數據組中(橫坐標為1),有13組預測準確,5組預測錯誤。整體預測準確度為71.43%。在僅有163組訓練集數據的情況下可以達到70%以上的準確度。

3.4 分類模型結果

使用205組金屬模式成分數據組進行分類模型計算,其中,僅使用元素成分結果,主觀賦值部分變量(包括器型、腐蝕程度、腐蝕種類賦值)不納入訓練集中。

對訓練集數據組進行分類,分別使用K-means 和HCA聚類算法進行分類。

3.4.1 HCA聚類

HCA算法以數據相似性為度量,計算每個樣本之間的距離,逐漸向上合并形成聚類。分類結果如圖所示,如果分成三類,可以按照圖中橙色、綠色、紅色來區分。其中橙色區域以銅兵器為主(幾乎全部銅矛、銅泡、銅刀、銅鈴、銅鉞),包含部分銅容器(如2000HDM54:155銅爵、2000HDM54:84銅爵等),紅色區域以銅容器為主(包括2000HDM54:392銅牛尊、2000HDM54:183方彝,及部分兵器和雜器如2000HDM54:151銅刀、2000HDM54:392銅手等。綠色區域器型特征明顯性較弱,容器、雜器和兵器均占有一定比例。

使用HCA算法進行聚類分類結果可以大致區分兵器和容器,但特征性較差。

3.4.2 K-means聚類

K-means通過將相似的數據點分組為簇來幫助解釋數據,利用肘部原則來選擇最佳的K值,也即是要分成的簇的數量。隨著 K 值增加,每種聚類結果的誤差平方和(SSE)通常會減小,但是當K值達到某個值時,SSE減少的程度會變得更加緩慢,形成一個“肘部”,選擇該肘部所對應的K值作為最優聚類數,提高聚類模型的效率與準確性(14)孫林、劉夢含、徐久成:《基于優化初始聚類中心和輪廓系數的K-means聚類算法》,《模糊系統與數學》2022年第1期。。由于本次研究的數據組包含多種變量(化學元素種類),先使用主成分分析(PCA)來減少數據維度,并在此基礎上運行K-means聚類算法。運算結果如圖7所示。

圖6 肘部原則折線圖顯示,K=2和K=3處出現轉折,此后直線斜率明顯減小,K=3之前為陡降區,K=3之后為緩降區,故選擇K=3,即將數據組分為3個類別。如圖7所示,圖中橙色點為三類中理想的典型點,實際并不存在,三個區域可以大致地按照容器、雜器和兵器區分,但三者并不能界限分明的區別開,同時存在較多混雜情況,區分度并不是特別理想。

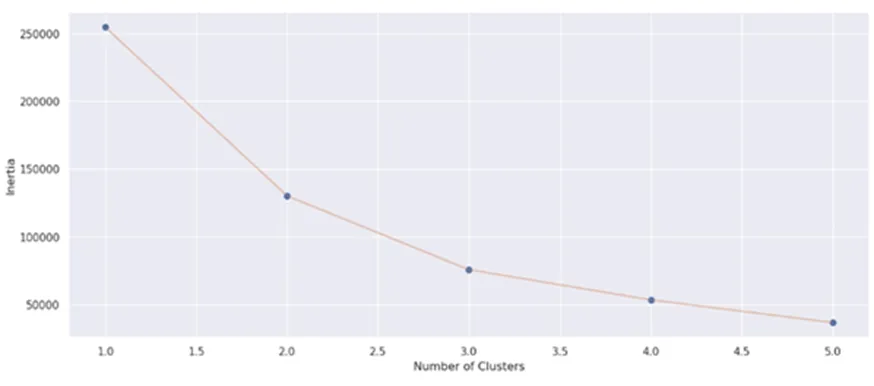
圖6 金屬模式訓練集肘部原則折線圖

圖7 金屬模式訓練集分類圖

3.5 討論

3.5.1 樣本本身代表性與特異性引入的模型誤差

本研究使用銅器表面的p-XRF數據進行機器學習的分析,樣本本身信息的代表性受到多重影響。首先,由于埋藏過程的長期腐蝕導致表面成分受到腐蝕產物不均勻分布的影響,且文物出土后經過不同程度的清理與不同方式的保護修復處理(粘接/焊接等),以及在博物館展廳與庫房保存環境不同導致的出土后不同的繼續腐蝕反應;其次,本研究中將器物分為容器、兵器、雜器三類,分類方式較為粗放,導致同一類別內本身存在較大差異;這些是樣本集中事實存在的不同代表性差別。就腐蝕而言,即便是同樣的埋藏環境、同樣的器型,根據葬儀產生的不同類型的內部盛裝物比如肉、骨、酒、植物類等以及殉狗身上的銅鈴等,也會產生腐蝕產物的差別,導致成分區別,這是樣本本身特異性差異。

在研究過程中還進行了器型-腐蝕狀態的相關分析,但是目前結果可解釋性較差,根據出土信息可以大概認識到容器與兵器的擺放分別存在一定的集中性,容器集中在槨室南部,兵器集中在槨室的北部和東部,通過對樣本信息采集過程的改良與預處理,未來工作可能通過分析顯示出顯示區域性環境導致的腐蝕病害集中情況。

3.5.2 方法的有效性

在討論相關性時,考慮整體樣本量較少且變量較多,同時存在較多特殊點,使用Spearman相關系數而不是傳統常用的Pearson相關系數。在相關性較強且符合正態分布的情況下,Pearson相關系數通常是一種有效的計算方式,而Spearman相關系數適用于非正態分布和存在外部影響(如離群點)的情況,能夠排除一些異常值和極端數據的影響,檢測到更廣泛的關系類型且不要求數據集滿足線性假設。對于受埋藏腐蝕后成分情況更為復雜的出土文物樣本成分數據處理,使用Spearman相關系數更有助于得出有效結果。

在相關性分析基礎上,使用機器學習進行元素-器型預測和聚類分析的過程中,由于目前相對變量而言樣本量過少,在建立統計模型時出現了過擬合的問題,在元素-器型關系預測中線性回歸、隨機森林、KNN、XGBoost等方法R2均大于1的現象。這是由于文物樣本本身由于腐蝕的發展表面成分與金屬基體成分存在一定差異,且本研究采用p-XRF檢測方法,存在較多的信號噪聲可能被誤以為是有效信號而造成過度學習。使用SVR算法魯棒性較好,且相對更適用于處理文物成分數據這類高維度數據并減少過擬合現象。

3.5.3數據改良方式探討

對于銅器表面成分的影響受到以下幾個方面影響:金屬基體原始成分、埋藏環境影響、埋藏過程的腐蝕、出土后的腐蝕、修復處理等,在機器學習數據采集過程中需要更明確的問題指向,提高樣本采集數量,盡量保證訓練集和測試集數據變量均在可討論范圍內。同時在明確研究問題時空范圍的前提下,盡量擴大有效訓練集本身,如考慮在同一器物上細化采集部位、增加數據采集點位來彌補腐蝕導致的同一器物成分差異,選擇腐蝕產狀一致的部位進行成分采集與比較;或全面采集同一單位內所有銅器,同時加入層位、區域信息作為新增變量,對訓練集中的特征信息賦值更明確;或使用標準統一的更為精確的p-XRF量化數據作為訓練集,避免采集過程引入的人為誤差。

四、結果與展望

機器學習已經廣泛應用于數據挖掘和分析、語音和圖像識別、自然語言處理、材料學研究等各個領域,應用前景非常廣闊。本研究利用機器學習來研究M54出土銅器的p-XRF表面成分數據,利用支持向量回歸算法SVR,K均值聚類算法K-means和層次聚類算法分別建立模型,摸索元素-元素、元素-器型之間的數據規律及關系,并使用直觀的圖形可視化形式進行展示;通過元素-器型預測模型較為準確的預測測試樣本元素成分對應的器型特征;使用分類模型對銅器表面成分進行分類,探討器物成型與腐蝕過程規律,提升了文物成分分析與研究的效率。

4.1相關性分析

通過計算Spearman相關系數討論銅器表面成分中元素與元素、元素與器型、元素與腐蝕之間的兩兩相關性。

通過對比Cu、Sn、Pb三個主量元素與各微量元素之前的相關性系數,Cu元素與Sn元素的顯著負相關(-0.9)及Sn元素對容器和兵器的正負相關性差異,與前期研究中圍繞錫料的合金配比人為控制的結論相吻合。新發現除Sn元素外,Ni、Co、Fe、Cr等元素也表現出分別與容器、兵器正負相關的特點,可能暗示古代工匠在不同功能器物冶煉過程中存在更多元的合金配比調整模式。在更高維的數據層面體現出不同元素可能的礦料原料來源區別,對于探討是否存在年代-區域框架下模式化的冶金行為具有一定意義。

另一方面,也證明了使用p-XRF對腐蝕銅器進行的無損表面成分數據,在經過合理的數據處理后同樣可以體現出銅器的合金配比信息,一定程度上避免了銅器成分分析必須使用金屬基體部分而進行的有損取樣行為。

4.2元素-器型預測模型

在相關性分析的基礎上,以金屬模式元素成分與器型賦值數據為訓練集,分別使用SVR、Linear Regression、KNN回歸算法、XGBoost、Random Forest等算法訓練模型,并使用混淆矩陣來評估模型的準確性。在僅使用163組數據作為訓練集的情況下,使用SVR算法達到的元素-器型預測準確度達到了71.43%。

本研究中相對變量較多而樣本總數較少,模型在訓練集上表現良好,但在測試集上表現較差。研究過程中使用的SVR方法的R2為0.971,而線性回歸、隨機森林、KNN、XGBoost等方法R2均大于1,出現過擬合現象。由于出土文物的p-XRF數據普遍具有維度高、變量多、回歸性較差的特點,使用SVR算法可以有效地處理高維度數據并減少存在于傳統回歸方法中的過擬合(overfitting)現象,在遇到有噪聲的數據時也可取得良好的預測結果。由于支持向量是使用部分樣本構造出的,所以在精度保證的同時具備一定的可解釋性。

建立元素-器型預測模型,可以為破碎嚴重、疊壓復雜的出土文物碎片信息識別和拼對修復提供指導;同時有也有助于更深入了解不同器型的元素特征及背后代表的礦料來源信息。

4.3 分類學習模型

在對成分數據進行分類時,分別使用HCA聚類算法和K-means聚類算法對205組金屬模式成分數據組進行分類模型計算,HCA聚類算法得到多層聚類分布結果,可以大致區分兵器和容器,K-means聚類算法根據肘部原則確定三相區分結果,但三者之間并不能界限分明的區別開,區分度都不是較為理想。

機器學習在出土文物研究中具有廣泛的應用前景,目前,本研究使用的數據量相對變量稍有不足,尚不足與得到理想的模型結果,但在未來工作中,在問題目標明確的情況下更大范圍、更精細地獲取數據支撐算法的推進驗證,預期能夠得到更貼近顯示的統計規律與預測模型成果。