基于模糊純追蹤模型的最優預瞄研究

楊旭升

摘 要：預瞄距離對于純追蹤模型的影響至關重要，面對線性預瞄距離和非線性預瞄距離兩種常見的預瞄距離選擇，本文通過將車輛速度、道路曲率、橫向偏差、航向偏差作為模糊控制器的輸入，得到預瞄距離系數K，代入兩種預瞄距離函數，探究在純追蹤模型的追蹤效果。通過模擬兩種預瞄距離在直線路段、曲線路段的追蹤效果，得到非線性預瞄在兩種路段追蹤效果更加優越，符合人類駕駛員的駕駛行為。

關鍵詞：模糊純追蹤 線性預瞄 非線性預瞄 橫向控制

1 引言

新能源汽車產業的蓬勃發展推動了自動駕駛概念進入大眾視野，從礦區、港口的特種智能汽車，到物流園區的無人分揀、配送車，在這其中，車輛運動控制是車輛安全平穩運行的最終保障。自動駕駛的控制系統可分為對汽車轉向機構的橫向控制，使車輛跟隨期望軌跡行駛，以及對車輛制動、加減速的縱向控制。智能汽車的路徑跟蹤根據使用傳感器的類型可分為預瞄式和非預瞄式[1]。非預瞄式橫向控制應用于車路協同式車輛，即根據路測的智能基礎設施獲取車輛當前位置與期望路徑的位置關系，控制車輛沿著期望路徑行駛[2]。預瞄式即模仿人類駕駛員在道路行駛時，根據車輛當前時刻速度、位置信息和期望路徑間的偏差，選擇一個合適的預瞄距離計算方向盤或車輛前輪轉向角度，達到預定軌跡。過于遠的預瞄距離可能會使車輛提前對后續路段做出反應，軌跡跟蹤效果偏離預期，過于近的預瞄距離可能會讓車輛跟蹤出現振蕩[3]，因此預瞄距離的選取對車輛跟蹤效果至關重要。

彭之川根據車速和道路類型選取不同的線性關系描述預瞄距離，使直道相較于彎道有更遠的預瞄距離[4]，劉凱考慮預瞄距離與車速的關系，提出了預瞄距離與車速呈二次非線性關系，更為貼合人類駕駛員在高速情況下觀察的實際情形[5]。郭壁璽將車輛橫向偏差和航向偏差作為模糊控制的輸入，計算得到不同情況下的車速增益[6]，張華強采用PSO算法自適應的計算預瞄距離，提升了車輛直線行駛時的精度[7]。但是，以上研究在探究預瞄距離對控制精度的影響時僅僅考慮車速、道路類型、橫向偏差等單個因素，為此本文在綜合考慮車速、道路環境、橫向偏差、航向偏差等影響因素的基礎上，使用模糊純追蹤模型探究線性預瞄距離、非線性預瞄距離對控制精度的影響。

2 理論模型

汽車運動學是從幾何學的角度研究物體的運動規律，包括物體在空間的位置、速度等隨時間而產生的變化，常見的運動學模型有以后軸為原點的車輛運動學模型、以質心為中心的車輛運動學模型、前輪驅動的車輛運動學模型等，本文采用以后軸為原點的車輛運動學模型。

2.1 二自由度汽車運動學模型

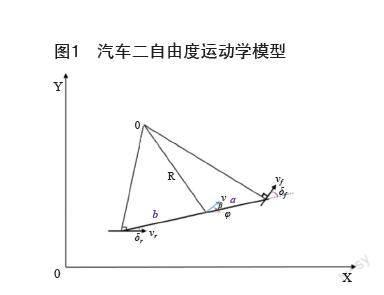
二自由度汽車運動學模型忽略了懸架的作用，將整車簡化為兩輪，認為輪胎側偏特性為線性，忽略側向力的作用，車輛不會進行俯仰及翻滾運動，始終在水平面運動，將汽車簡化為線性二自由度模型可表示為圖1所示。

根據幾何關系和速度關系推導可得出：

其中XOY為大地坐標系，φ為橫擺角，即車輛軸線與X軸方向夾角，β為質心偏側角，即質心速度與車輛軸線的夾角，R為車輛轉向半徑，O為車輛瞬時轉向中心，v為車輛的質心速度。在三角形中由正弦定理：

其中a，b分別為質心到前后軸的距離，由于車輛重量會影響質心位置，導致a，b長度改變，引入軸距L可得：

其中δf為前輪轉角，δr為后輪轉角。在低速狀態下，認為車不會發生測向滑動，由vy≈0，可得。一般后輪不轉向，即δr≈0，則有：

2.2 純追蹤模型

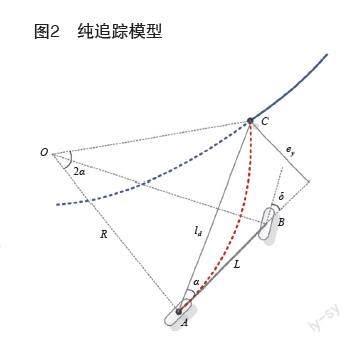
純追蹤算法通過將車輛從當前位置到目標位置間畫一條圓弧，使車輛遵循一條經過目標點的圓弧行駛，在低速情況下可將車輛簡化為兩輪自行車模型，可將其簡化為圖2所示[9]。其中XOY表示大地坐標系，xoy表示車輛坐標系，L為車輛軸距，ld為車輛后軸到預瞄點的距離，ey為車輛距離預瞄點的橫向距離，α為預瞄距離ld與車身軸線所處夾角，R為車輛轉向半徑。

在三角形OAC中由正弦定理：

可以得到：

由式（4）車輛的運動學方程有：

代入上式可得：

3 模糊控制器設計

將式（8）進一步處理可知，預瞄距離對車輛前輪轉角的影響更大，其選取的結果直接影響車輛對規劃軌跡的追蹤效果，一種最常見的調整預瞄距離的方法就是將其表示成車輛縱向速度的線形函數，即

（9）

其中t表示預瞄時間，Lfmin表示最小預瞄距離，K為預瞄距離系數。

劉凱提出了一個車速的非線型函數[10]：

其中第一項表示車輛制動距離，，amax代表車輛最大制動加速度，第二項表示車輛碰到異常情況進行反應的車輛行駛距離，C表示車輛最小轉彎半徑。

為了得到參數K，按照人類駕駛員的駕駛經驗，設定以下的預瞄距離規則：（1）速度越大，預瞄距離越遠；（2）曲率越大，預瞄距離越近；（3）橫向偏差越大，預瞄距離越近；（4）航向偏差越大，預瞄距離越近。

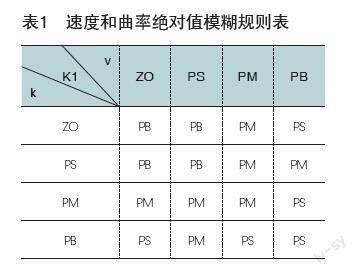
根據這個經驗規則，我們選取速度、當前道路曲率、橫向偏差、航向偏差作為模糊控制器的輸入，輸出為系數K，將計算的參數K代入兩種預瞄距離，探究其優越性。表1、表2為計算預瞄距離系數K的模糊規則表，對經過模糊控制輸出的系數K1、K2賦權重得到最后系數K。其中表1將速度v和曲率絕對值k作為模糊控制器的輸入，輸出為系數K1，表2將橫向偏差?E、航向偏差?Yaw作為模糊控制器的輸入，輸出為系數K2。最終系數K由公式K=αk1+βK2（α+β=1）得到。

將速度v和曲率k的絕對值劃分為4個模糊集合，橫向偏差?E、航向偏差?Yaw劃分為7個模糊集合，模糊集合的劃分可以均勻劃分也可不均勻劃分，本文模糊集合的劃分按不均勻劃分。

4 仿真與分析

為了模擬真實環境中可能出現的道路情況，將仿真道路分為直線與曲線路段，其中直線段為一次函數型直線，曲線段為正弦函數型曲線，使用Matlab搭建模型，對式（9）線性預瞄時間t取2.5，Lfmin取1，得到線性預瞄距離函數，對式（10）非線性預瞄距離函數amax取3，B取0.2，C取1.5得到，車輛軸距L=0.9。

4.1 直線路段追蹤效果

直線段函數表達式為y=4x+0.4，x∈[0，10]，車輛初始條件[x（0），y（0），yaw（0），v（0）]=[0，-0.5，-0.5，0]，直線路段的追蹤如圖3所示，追蹤誤差如表3所示。

在車輛初始條件偏離規劃軌跡初始點的場景下，非線性預瞄相較于線性預瞄更快貼合規劃軌跡，比線性預瞄提前3米將誤差趨于穩定，而線性預瞄在0-2米內誤差在持續增大，在實際應用場景中有較大的危險隱患。由表3可知，相較于線性預瞄，非線性預瞄各項數據均優于線性預瞄，跟蹤誤差更加平滑、波動更小，追蹤效果更好。

4.2 曲線路段追蹤效果

曲線段函數表達式為y=sin（x/2）*x/2，x∈[0，10]，車輛初始條件[x（0），y（0），yaw（0），v（0）]=[0，-0.5，-0.5，0]。曲線路段的追蹤如圖4所示，追蹤誤差如表4所示。

非線性預瞄在車輛初始條件偏離規劃軌跡初始點的場景下，相較于線性預瞄追蹤效果更佳，但因為預瞄距離變化過大引起前期出現短暫振蕩，可對預瞄距離選取做相應限制得到改善。線性預瞄在曲線路段全程存在追蹤偏差過大的問題，在實際場景的連續轉彎路段追蹤偏差會過大，同時由表4可知，非線性預瞄在追蹤誤差方面比線性預瞄變化幅度更小，收斂更快。

5 結語

本文綜合考慮車輛速度、道路曲率、橫向偏差、航向偏差等多種影響預瞄距離的因素，通過模糊控制器輸出預瞄距離系數，結合純追蹤算法，得到車輛前輪轉角。通過模擬線性預瞄函數和非線性預瞄函數在直線型路段、曲線型路段的追蹤效果可知，非線性預瞄相比于線性預瞄誤差收斂更加快、誤差變化幅度更加小、追蹤效果更加顯著。但是當偏離規劃軌跡較遠時，非線性預瞄前期會有短暫的振蕩現象，可通過限制預瞄距離梯度加以改善。由此可知，結合多種影響因子，使用非線性預瞄函數在模糊純追蹤算法中有著更加顯著的追蹤效果，非線性預瞄函數也更加符合人類駕駛員實際的駕駛行為。

參考文獻：

[1]趙熙俊，陳慧巖.智能車輛路徑跟蹤橫向控制方法的研究[J].汽車工程，2011，33（05）：382-387.

[2]高琳琳，戎輝，唐風敏，郭篷，何佳.自動駕駛汽車橫向運動控制方法綜述[J].汽車電器，2019，（09）：1-4.

[3]段建民，楊晨，石慧.基于Pure Pursuit算法的智能車路徑跟蹤[J].北京工業大學學報，2016，42（09）：1301-1306.

[4]彭之川，朱田，易慧斌.基于改進的Pure Pursuit智能客車軌跡跟蹤算法研究[J].客車技術與研究，2019，41（05）：21-24.

[5]劉凱．無人駕駛車輛體系結構與定位導航技術研究 [D]．北京：北京理工大學，2010．

[6]郭璧璽，杜興樂，陶小松.基于純追蹤模型的算法改進[J].汽車實用技術，2019，（15）：32-34.

[7]張華強，王國棟，呂云飛，秦昌禮，劉林，宮金良.基于改進純追蹤模型的農機路徑跟蹤算法研究[J].農業機械學報，2020，51（09）：18-25.

[8]忠厚老實的老王.三個坐標系與運動學方程.https：//www.bilibili.com/video/BV1gh411o7WJ.

[9]https：//img-blog.csdnimg.cn/20210418094129716.png？x-oss-process=image/watermark，type_ZmFuZ3poZW5naGVpdGk，shadow_10，text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L1Jvbm5pZV9IdQ==，size_16，color_FFFFFF，t_70.

[10]劉凱.無無人駕駛車輛體系結構與定位導航技術研究[D].北京：北京理工大學，2010.