基于動態博弈理論的污水處理廠PPP項目風險分擔研究

劉清連,荀志遠,常海旭,馬 菱,邱現樂

(青島理工大學 管理工程學院,青島 266525)

經過多年的實踐與發展,污水處理廠的投資、建設、運營等經歷了眾多方式,包括政府獨資模式、BT模式、BOT模式和PPP模式等,經過長期實踐證明,政府獨資、BT等模式由于不能充分發揮項目各參與方優勢而導致項目受限。PPP模式具有可以擴寬融資渠道、吸引多方機構參與以及提高管理效率的優點[1],能夠有效促進污水治理行業的發展。黨的十八大以來,政府明確指出,新建污水處理廠若有政府參與,一律使用PPP模式,平穩推進庫存項目向PPP模式轉型。

PPP模式能夠充分利用政府和社會資本方等各方特長,有效解決資金緊張問題,提高項目建設和運營效率。但是參與方的增多,導致風險因素增加,有些風險因素涉及多個參與方[2],分擔界限模糊,需要明確界定此類風險分擔比例。

為此,專家學者對PPP項目中風險分擔問題開展了研究。采用的研究方法可分為四類:第一類是通過案例分析的方式總結風險分擔原則,如MOURAVIEV[3]對卡拉干達市的正在進行的11所幼兒園PPP項目,通過案例分析的方式,尋找公私雙方之間的風險分配的基礎原因。鄧斌超等[4]通過案例分析與文獻梳理識別歸類再談判風險分擔的因素。但是此類方法針對的是相似類型或者單一的案例來進行風險分擔的研究,得到的結論缺乏普適性。第二類采用問卷調查的方式對風險分擔問題進行研究,如ALMARRI等[5]采用問卷調查方式來探究風險成本對風險分配的影響,為PPP項目利益相關者拓寬了風險分擔路徑。周和平等[6]同樣對具有代表性的12個PPP項目用案例分析法進行分析,識別出了影響風險再分擔的9個因素。但是這種方式用作風險分擔過程的主觀性太強。第三類研究方法是運用模糊數學理論,例如ALIREZA等[7]以混合模糊方法和控制論分析網絡過程(CANP)模型的形式提出一種方法對共擔風險進行識別;王亦虹等[8]通過區間模糊Shapley值進行收益風險分配模型的構建,探究各利益方的收益風險分擔方式。這種方式得到的風險分擔結果可靠性強,由于分配過程較復雜,不易實施。第四類方法是運用博弈理論來進行研究,如李林等[9]通過構建參與方在對稱與不對稱條件下的博弈模型,進行公私雙方風險分擔比例的求解;李妍等[10]通過考慮公私及金融部門三方出價順序的不同,構建風險再分擔動態博弈模型,最終得出了三方風險分擔比例;楊琳等[11]通過構建討價還價風險分擔博弈模型,對地下綜合管廊PPP項目的政府與社會資本方應分擔的具體風險比例進行求解。但是以上學者在進行風險分擔博弈模型建立的同時,忽略了涉及到的風險相關參數的數值是否可靠這一問題,降低了模型結果的可信度。部分學者的參數數值通過專家問卷打分的方式獲取,未考慮相關專家在進行評判時,存在的主觀偏好或是不確定程度對參數數值造成的不準確結果。

本文基于動態博弈理論建立公私雙方的風險分擔博弈模型,模型相關參數的確定采用專家打分法,考慮到專家的主觀偏好和認知模糊等問題可能會讓結果偏離實際,引入猶豫度方法降低主觀性帶來的結果不合理問題,使得出的參數更符合實際情況,將建立的模型應用于某污水處理廠PPP項目,得出污水處理廠PPP項目共擔風險的具體分擔比例,研究結論對提高政府和社會資本方在污水處理廠項目上的合作效率,促進污水處理廠PPP項目的高質量發展具有重要意義。

1 風險分擔動態博弈模型分析

1.1 政府部門與社會資本方動態博弈過程

在博弈過程中,政府優先提出風險分擔比例,社會資本方以此做出策略選擇,若接受政府部門提出的決策,則談判結束;若反對其策略,則開始第二回合談判,直到所提出的策略讓雙方所獲利益都是最佳的,則談判結束。雙方之間的風險分擔動態博弈過程如圖1所示。

圖1 政府部門與社會資本方動態博弈過程

1.2 基本假設

假設一:污水處理廠PPP項目中的當地政府與社會資本方都是有限理性的經濟人。

假設二:當地政府與社會資本方之間的信息具有不對稱性。

假設三:各個風險之間不具備關聯性,彼此之間互不影響。

假設四:在談判過程中,在第j回合,政府部門提出愿意承擔的風險分擔比例為kj,則社會資本方承擔的風險比例為1-kj。

假設五:由于污水處理廠項目為公益事業,考慮政府部門占主導地位,首先提出風險分擔比例。

1.3 相關參數分析

1.3.1 參數分析

1) 談判損耗因子(θ)。談判損耗因子即談判成本,取值大于1,包括政府部門談判損耗因子θg,社會資本方談判損耗因子θp。在談判過程中,會增加時間、物力、財力以及人力等成本,隨著時間的增加,談判成本會更大,雙方所承擔的風險也更大,因此在進行雙方風險分擔比例計算時,在風險值前應乘以大于1的θg與θp。由于社會資本方在污水處理廠PPP項目風險分擔談判過程中處于劣勢地位,隨著時間的增加,談判成本相比于當地政府更大,因此社會資本方的談判損耗因子θp大于政府的談判損耗因子θg。

2) 風險轉移份額(λ)。在對風險分擔比例談判過程中,優勢方會由于其主導地位向劣勢方轉移一部分風險,以此來確保自己的利益最大化。假如在第i回合的談判中,政府部門向社會資本方轉移風險份額為λi,則政府部門的總風險會減少λi,社會資本方的總風險會增加λi。

3) 風險轉移概率(ρ)。在污水處理廠PPP項目中的風險分擔談判過程中,雙方獲取的信息是不對稱的,因此社會資本方并不知曉當地政府部門是否會向己方轉移風險,但是轉移的概率可以通過主觀確定。可以假設當地政府部門轉移風險的概率為ρ,不轉移風險的概率為1-ρ。

1.3.2 基于猶豫度的參數分析

本文參數確定的方式采用專家打分法,考慮到專家在對相關參數進行評價時,由于主觀偏好與認知偏差可能會造成結果的不合理性,降低模型可信度。首先將專家評分時語言變量轉化為直覺模糊數(IFNs),然后根據評價信息猶豫度方面計算出專家猶豫度權重,最后集結專家的實際評分與猶豫度權重,得出較為合理的風險相關參數。

1) 猶豫度定義。

定義[12]設X是一個非空集合,A={〈x,μA(x),vA(x)〉|x∈X}為直覺模糊集,其中μA(x)和vA(x)分別為X中元素x∈X的隸屬度μA:X→[0,1]和隸屬度vA:X→[0,1],且滿足條件0≤μA(x)+vA(x)≤1,?x∈X。此外,πA(x)=1-μA(x)-vA(x)為A中元素x的猶豫度,滿足條件0≤πA(x)≤1。稱a=(μa,va,πa)為猶豫模糊數(IFN),簡寫為a=(μa,va)。

2) 語言變量與IFNs的轉換。參照文獻[13]的語言變量與IFNs的轉化關系,考慮到不同專家相異的猶豫度水平以及專家在相關領域從事年限、經驗等不同,猶豫程度不會有較大的差異,故將專家的猶豫度等級分為“極小”“小”“一般”,分別對應π=0.1,0.2,0.3,得到專家評分時的語言變量與IFNs的轉化關系,見表1。

表1 語義信息與IFNs轉化

3) 基于評價猶豫度的專家權重計算步驟:

a) 確定共擔風險集合為R={R1,R2,…,Rn},假定每個風險對應相關參數集合為C={Cj,j=1,2,3,4},其中C1=θg,C2=θp,C3=λ,C4=ρ,專家集合為D={D1,D2,…,Dm}。

c) 基于猶豫度的專家權重確定。專家對風險相關參數進行評分時的不確定程度用猶豫度來表示。以專家Dk為例,整體猶豫度πk計算見式(1):

(1)

πk值越大,表示專家的猶豫程度越高,結果的不合理性越高[14],據此得到基于猶豫度的專家Dk的權重ωk:

(2)

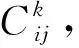
(3)

(4)

(5)

2 博弈模型構建

2.1 模型的建立

1) 第一回合談判。在第一回合談判中,污水處理廠PPP項目的地方政府首先提出愿意分擔風險的比例為k1,社會資本方承擔剩下的1-k1風險分擔比例,社會資本方同意分擔則談判在第一回合結束;不同意分擔,談判進入第二回合。假設社會資本方同意當地政府提出的風險分擔比例。在談判過程中,政府部門可能利用其強勢地位向社會資本方轉移風險份額λ1,轉移的概率為ρ。則政府部門(G)和社會資本方(P)的風險分擔期望值分別為

G11=ρ(k1-λ1)

(6)

P11=ρ(1-k1+λ1)

(7)

當以1-ρ的概率不利用其強勢地位時,雙方的風險分擔期望值分別為

G12=(1-ρ)k1

(8)

P12=(1-ρ)(1-k1)

(9)

第一回合談判,政府部門(G)和社會資本方(P)的風險分擔期望值分別為

G1=G11+G12=ρ(k1-λ1)+(1-ρ)k1

(10)

P1=P11+P12=ρ(1-k1+λ1)+(1-ρ)(1-k1)

(11)

2) 第二回合談判。社會資本方在拒絕政府部門提出的風險分擔策略的前提下,談判進入第二回合。社會資本方在基于自己的效益前提下提出愿意承擔的風險比例為1-k2,則政府部門承擔的風險比例為k2,政府部門利用其強勢地位向社會資本方轉移風險份額λ2的概率為ρ。隨著談判時間的延長,談判成本也會隨之增加。假設政府部門和社會資本方的談判損耗因子分別為θg,θp。則雙方風險分擔期望值分別為

G21=θgρ(k2-λ2)

(12)

P21=θpρ(1-k2+λ2)

(13)

當政府部門以1-ρ的概率不利用其強勢地位時,雙方的風險分擔期望值分別為

G22=θg(1-ρ)k2

(14)

P22=θp(1-ρ)(1-k2)

(15)

第二回合談判,政府部門(G)和社會資本方(P)的風險分擔期望值分別為

G2=G21+G22=θgρ(k2-λ2)+θg(1-ρ)k2

(16)

P2=P21+P22=θpρ(1-k2+λ2)+θp(1-ρ)(1-k2)

(17)

3) 第三回合談判。當政府部門不同意社會資本方提出的風險分擔比例,進入第三輪博弈,博弈過程同上。政府部門(G)和社會資本方(P)的風險分擔期望值分別為

(18)

(19)

由此重復下去,直到達到污水處理廠PPP項目風險分擔最佳比例。

2.2 模型求解

此類動態博弈是一個無限進行下去的過程,使用一般的數學模型求解方法無法分析,在進行模型的求解前,需要引入海薩尼轉換[15]。海薩尼轉換將不完全信息博弈轉化成了完全但不完美信息動態博弈,分為兩階段動態博弈,第一是“自然人”的行動,第二是除自然人以外參與人的靜態博弈。

根據海薩尼轉換,以及三回合博弈模型的分析,奇數回合的談判博弈行為是無差別的。令第三回合的談判過程是逆推基點,假設在第二回合中社會資本方給出的策略,使當地政府在第二回合風險期望值大于第三回合,即G2>G3,當地政府為了自身利益最大化,會拒絕第二回合談判,直接進入第三回合談判。但是在實際談判博弈中,隨著談判時間增加,談判成本不斷加大,造成雙方都有一定損失,為了利益最大化,雙方會盡力讓談判在第二輪結束,使G2≤G3,因此最佳結果為

G2=G3

(20)

(21)

即

k2=ρλ2+θgk3-ρθgλ3

(22)

將式(22)代入式(17),得

P2=θp(1-θgk3+ρθgλ3)

(23)

又

(24)

P2-P3=θp[1-(θg+θp)(ρλ3-k3)+θp]

(25)

因為θp>θg>1,1≥k3>λ3≥0, 0≤ρ≤1,故P2-P3<0,因此公私雙方不會將談判拖到第三回合。

繼續將逆推點設置在第二回合,假設當地政府在第一回合提出的風險分擔比例使得社會資本方在第一回合談判的風險期望值大于第二回合,即P1>P2,社會資本方會拒絕第一回合討價還價博弈,直接進入第二回合,由于繼續下去,談判成本會增加,雙方為了保證自身利益,會讓談判在第一回合結束,此時最佳策略為

P1=P2

(26)

將式(17)(23)代入式(26),得

ρ(1-k1+λ1)+(1-ρ)(1-k1)=θp(1-θgk3+ρθgλ3)

(27)

求得

k1=1+ρk1-θp(1-θgλ3+ρθgλ3)

(28)

因為奇數回合,動態博弈模型結構是無差別的[16],故

k1=k3

(29)

將式(29)代入式(28),得

k1=[θp-1+ρ(θgθpλ3-λ1)]/(θgθp-1)

(30)

1-k1=[θp(θg-1)-ρ(θgθpλ3-λ1)]/(θgθp-1)

(31)

設風險轉移份額λ為常數,則最終均衡解為

k*=(θp-1)/(θgθp-1)+ρλ

(32)

1-k*=(θgθp-θp)/(θgθp-1)-ρλ

(33)

在污水處理廠PPP項目中,當地政府與社會資本方需承擔的風險分擔比例分別為(θp-1)/(θgθp-1)+ρλ與(θgθp-θp)/(θgθp-1)-ρλ。

2.3 模型結果分析

1)k*是政府部門的名義風險分擔比例,實際風險比例為(θp-1)/(θgθp-1),ρλ是政府部門轉移給社會資本方的風險份額。當ρ=0時,表示政府部門利用強勢地位向社會資本方轉移風險份額的概率為零;當ρ=1時,屬于完全信息條件下的風險分擔談判博弈,此時政府部門向社會資本方轉移風險份額為肯定的結果。在實際風險分擔討價還價博弈中,即0<ρ<1時,此時博弈處于不完全信息條件下,政府部門尚無法確定社會資本方能力大小,向社會資本方轉移多少風險份額是一個未知數,相比在完全信息條件下,轉移的風險份額更小。

2) 談判損耗因子與所獲效益相關。假如在每次的談判中,不考慮風險轉移,降低談判成本,則談判損耗因子會減少。由于社會資本方的談判損耗因子基數高于當地政府部門,其降低的幅度會更大,社會資本方在承擔高于政府部門的風險同時,也獲得了略高于政府部門的增量效益,因此在動態博弈過程中,社會資本方應盡可能將談判成本控制在最低水平,保證自己能夠獲得最大增量效益。

3 算例分析

某污水處理廠PPP項目總投資約9130.86萬元,其中一期建設總投資7144.68萬元,特許經營期為30年。通過咨詢與項目密切相關的人員,包括政府部門與社會資本方等在內的12位負責人,確定該項目的風險談判過程為不完全信息條件下的動態博弈。通過查閱該污水處理廠PPP項目的相關資料,得到通貨膨脹等7個重要的共擔風險,現進行風險分擔分析。

3.1 風險相關參數確定

由于篇幅有限,以調查問卷的方式邀請了9位在PPP模式方面經驗豐富的專家群進行評分。為了便于專家打分,根據各參數的取值范圍將各個參數劃分為很低、較低、中等、較高及很高5個等級,每個等級對應1個確定的數值,見表2。

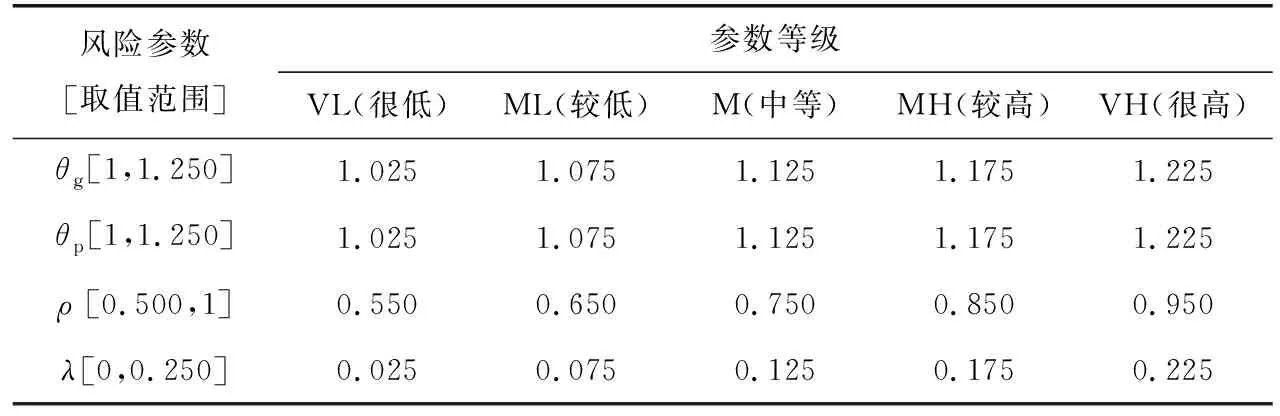
表2 風險相關參數等級劃分標準

專家在打分時,根據自身專業水平以及對信息不確定程度進行猶豫等級的選取。所有專家對各風險相關參數的原始語義評價信息見表3,其中下標表示猶豫等級,“1”“2”“3”分別對應“極小”“小”“一般”。

表3 專家群對各風險相關參數的原始語義評價

步驟1。由于篇幅有限,僅列舉專家D1經轉化的語義評價信息的猶豫模糊矩陣。根據表3專家評分的原始語義信息轉化為猶豫模糊數,得到專家D1的猶豫模糊矩陣:

步驟2。根據式(1)(2)計算出各個專家基于猶豫度的專家權重,分別為ω1=0.105,ω2=0.109,ω3=0.109,ω4=0.119,ω5=0.099,ω6=0.119,ω7=0.099,ω8=0.125,ω9=0.114。

步驟3。根據式(3)—(5)結合表3,得到基于猶豫度權重處理后的區間風險相關參數,見表4。

表4 某污水處理廠PPP項目基于猶豫度權重處理后的風險相關參數值

3.2 風險分擔比例確定

根據表4,以通貨膨脹風險為例,在政府部門首先提出風險分擔比例的動態博弈模型中,由式(32)(33)得到:

政府部門對于通貨膨脹風險承擔的名義份額為

社會資本方對于通貨膨脹風險承擔的名義份額為

1-k*=1-0.758=0.242

政府部門對于通貨膨脹風險承擔的實際份額為

社會資本方對于通貨膨脹風險承擔的實際份額為

1-k**=1-0.653=0.347

同理可得其余風險分擔比例數值,見表5。

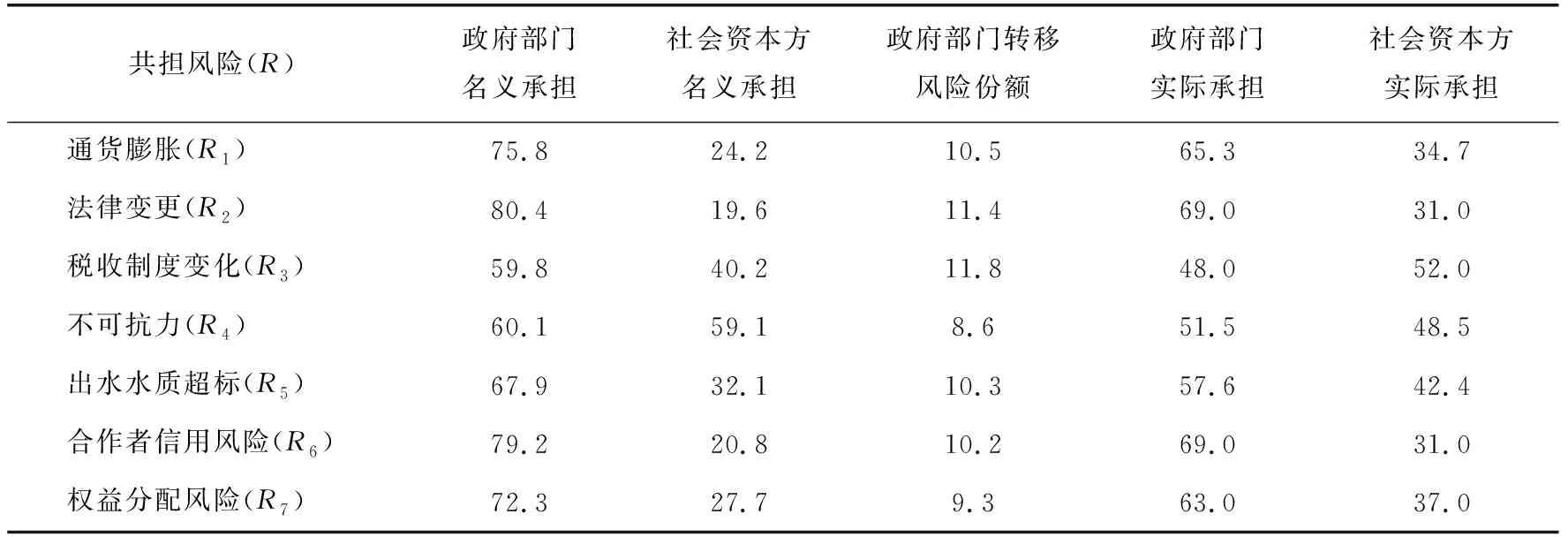
表5 某污水處理廠PPP項目風險分擔比例 %

3.3 結果分析

由表5可知:

1) 由于政府部門利用主導地位向社會資本方轉移了風險份額,故政府部門實際承擔的風險份額小于其名義承擔的風險份額;

2) 對于稅收制度變化、法律變更等風險,政府部門轉移的風險份額分別為 11.8%,11.4%等;對于不可抗力風險,政府部門轉移的風險份額為8.6%。從雙方對風險的承受能力上分析可知,稅收制度變化等風險都屬于政策上的風險,當這類風險發生時,政府掌握的政策信息較多,承受風險的能力更強,在這類風險的控制上占據高主導地位,向社會資本方轉移的風險份額較多;不可抗力風險屬于自然風險,當這類風險發生時,政府與社會資本方所掌握的信息差別不大,兩者承受風險的能力基本對等,相對稅收制度變化等風險來說,政府部門在不可抗力風險上占據低主導地位。因此,隨著政府對于某類風險占據的主導地位越強,在這類風險上的分擔上,向社會資本方轉移的風險份額就越多。

4 結論

本文基于動態博弈理論,針對污水處理廠PPP項目的風險分擔問題,構建政府和社會資本方風險分擔動態博弈模型,通過考慮評價信息猶豫度的專家權重確定方法來求取模型中的風險相關參數,得出雙方風險再分擔比例。分析可知,政府部門和社會資本方的風險承擔份額與談判成本的大小、公私雙方地位不平等、信息不對稱等因素具有關聯。在雙方信息不對稱情況下,政府部門能夠利用強勢地位將談判的一部分風險份額轉移給社會資本方,隨著談判回合增加,談判成本加大,社會資本方承擔的風險也會增大;政府部門占據的主導地位越高,向社會資本方轉移的風險份額越大。因此為了避免不必要的損失,雙方應盡可能多獲取對方信息,加大信息對稱局面。

根據上述分析,提出如下建議:

1) 加快建立或者完善風險分擔方面政策、法律,力爭做到公平公正合理。建立PPP項目風險分擔方面的法律、政策體系,約束公私雙方向對方轉移風險的行為,避免談判博弈過程中機會成本的增加,降低談判損耗因子,達到“共贏”局面。

2) 政府部門應以民生為首要任務,協助污水處理廠PPP項目加快落實。污水處理廠PPP項目屬于公共項目,最終目的是建設共享共存的人類環境,提高民生。政府在與社會資本方合作過程中,應秉承公平公正原則進行風險承擔,使風險分擔談判能夠盡快結束,落實污水處理廠項目,加快投入使用。

3) 建立信息共享平臺,加大信息對稱局面。為了減小風險不對稱局面帶來的政府部門向社會資本方轉移風險的問題,應加快建立信息共享平臺,使社會資本方盡可能多的獲取政府部門信息,加大信息對稱局面,減小其在談判過程中的成本,以便提高社會資本方在污水處理廠PPP項目建設中的積極性。

4) 引入第三方監督機構,使風險分擔規范化。為了避免在風險分擔談判過程中,公私雙方在私下達成協議,運用不良手段使雙方利益最大化,損害公共利益,可以引入第三方監督機構,從項目選擇到項目運營過程全程監督,設置多方舉報渠道,保證污水處理廠PPP項目的建成真正做到對公共事業有益。

總之,公私雙方風險分擔應從項目全生命周期入手,考慮每階段雙方所處地位、風險轉移的大小及信息不對稱局勢等影響因素,以期談判損耗系數的降低,使雙方達到風險分擔的共贏局面。在實際操作中,風險分配并不是處于理想情況,會受到多方因素的影響,因此今后研究應從博弈理論出發,考慮風險分配中的其他研究主體與內容,使模型的實際運作更加貼近實際污水處理廠PPP項目。