無信號控制交通場景的人車博弈行為分析及決策建模

李海洋,曲大義,*,楊子奕,陳意成,邵德棟

(青島理工大學 a.機械與汽車工程學院;b.土木工程學院,青島 266525)

在發展中國家,行人交通在城市交通系統中占據主導地位[1]。資料顯示,我國城市交通出行中,超過1/5為行人交通[2]。行人交通雖然是所有交通方式開始和結束必不可少的組成部分[3],但因其存在易受傷害等自身特點與車流交通相比呈現弱勢[4-5]。數據顯示,全球每年約有百萬人死于交通事故,其中約50%為行人和自行車騎行者[6],我國發生在無信號控制人行橫道區域的行人事故超過1/3,其中死亡事故占比超過37%[7]。無信號控制的路段和交叉口斑馬線處,由于缺乏交通信號燈和相應的空間渠化措施,難以分離行人和車輛在時、空上的通行權,因此易造成人車沖突,危及交通安全[8-9]。由此可見,無信號控制場景下,行人過街過程中存在人-車沖突,分析人-車沖突的決策過程和決策影響因素對于揭示人-車沖突機理,減少人-車沖突事故具有重要意義。

近年來,針對人車沖突與博弈決策行為分析,國內外學者做了部分研究,如YAN等研究了右轉車輛和過街行人之間的相互作用和博弈過程,建立了元胞自動機模型[10];QIU等對路口交通參與者的交通行為進行研究,構建了交通行為博弈模型[11];周雪峰等針對無信號控制路段上行人與車輛存在搶行的問題,建立了完全信息靜態和動態兩種博弈模型[12];劉博通分別分析了車輛和過街行人對風險的感知情況及二者的決策行為,得到了二者感知風險的變化規律和影響決策行為的因素[13];劉麗娟等基于博弈論,對行人和車輛的決策行為過程進行分析,建立了只考慮時間因素、同時考慮時間和風險因素的支付矩陣,并討論了Nash均衡[14];王璐等提出了基于臟臉博弈的模型,分析了車型、行人等待時間和個體認知能力異質性對人車沖突的影響[15];CHENG等使用不完全信息動態博弈模型研究了人車通行的碰撞風險,揭示了人車博弈中行人最佳決策與車輛運行速度存在相關性[16];李新波建立了人車博弈模型,應用累計前景理論選出博弈雙方的最佳策略[17];楊玉婷以時間和安全效用函數構造博弈收益矩陣,建立了基于沖突的不完全信息靜態博弈模型[18];韓喜雙等將人車博弈分為行人先行和車輛先行兩類情景,利用擴展式博弈模型,揭示了行人過街決策機理[19];魏麗英等建立了人車沖突演化動力學模型[20];雷愛國等將過街行人心理分為3個階段,并構建各階段的人車博弈矩陣,分析均衡點表明:行人和車輛演化博弈最終有2個穩定狀態[21];鄺先驗等將車輛分為禮讓與不禮讓2種類型,并考慮機動車禮讓比例,在元胞自動機模型的基礎上,引入動態博弈更新規則,模擬無信號控制處的交通沖突[22]。

綜上所述,國內外學者在對人車沖突進行博弈解析的過程中,往往將行人和車輛的行動簡化為單純的合作博弈或非合作博弈模型,沒有對博弈的階段性變化和行人的主觀因素進一步考慮,難以體現人車沖突時,行人與車輛駕駛人生理、心理的動態變化過程和決策的變化性。因此本文將利用靜態博弈模型、不完全信息動態博弈模型對人車決策全過程進行分析,同時考慮行人的生理、心理特性,進一步解析無信號控制場景下的人車沖突。

1 人車沖突現象分析

在無信號控制的交叉口和路段斑馬線處,行人與車輛常產生路權沖突,常見的人車沖突場景包括:

1) 車輛距離斑馬線較遠(滿足行人安全心理距離),行人能夠以正常速度通過。此時,行人與車輛可達成共識:行人安全通過后,車輛駛過斑馬線。

2) 車輛距離斑馬線很近(明顯小于停車視距),行人無法安全通過。此時,行人與車輛可達成共識:行人等待車輛通過斑馬線后再通過。

3) 車輛距離斑馬線位置較為“尷尬”(介于停車視距與安全心理距離之間),行人和車輛均可嘗試先行通過。此時,行人與車輛常常難以達成共識,會出現雙方相互打手勢、一方或雙方同時加速或減速、車輛摁喇叭等行為。

其中,場景1),2)情況都較為簡單,行人與車輛能夠直接達成共識。而場景3)較為復雜,行人與車輛往往需要1輪至多輪博弈才能達成共識。

博弈雙方行人和車輛均有兩個策略可以選擇,即通過與不通過。可將行人的策略合集記為Sp={C,D},C表示穿越,D表示等待;將車輛的策略合集記為Sc={T,R},T表示通過,R表示讓行。由于行人與車輛各有兩種策略,因此初始決策時會出現如表1所示的4種情況:

表1 純策略矩陣

情況①:行人選擇穿越,車輛選擇通過。此時對應上述沖突場景3),說明行人與車輛在第一階段的博弈中互不相讓,易產生交通事故。因此在這種情況下,行人與車輛接下來會進行第二階段博弈,以達到安全通過的目的。

情況②:行人選擇穿越,車輛選擇讓行。此時對應上述沖突場景1),行人能夠安全過街,同時車輛也能在行人過街后安全通過。

情況③:行人選擇等待,車輛選擇通過。此時對應上述沖突場景2),行人無法安全過街,因此行人只能等待車輛通過后再過街。

情況④:行人選擇等待,車輛選擇讓行。此時對應上述沖突場景3),說明行人與車輛在第一階段的博弈中互相讓行,導致雙方均無法通行。此時行人與車輛會進行第二階段博弈,以達到通行的目的。

通過上述分析不難發現,行人與車輛在一開始就能達成一方讓行,另一方通過是最為高效的,即情況②③。但行人與車輛在第一階段博弈失敗,產生了互不相讓和互相讓行的情況也較為常見,即情況①④。對于情況①④,接下來就進入到人車博弈的第二階段——序貫博弈的過程,即行人與車輛一方先決策,另一方后決策。

2 博弈影響要素分析

博弈主要由博弈參與者、策略以及策略對應的收益構成[23]。影響人車博弈過程的因素主要包括行人等待時間、策略選擇概率、行人緊張度、策略支付,同時也將延誤、風險度、行人風格和車輛駕駛人風格等融合考慮。

2.1 行人等待時間

行人過街心理與行人等待時間相關,行人等待時間越長,行人心理越容易變得急躁和不耐煩,進而導致行人冒險過街的概率增高。盧守峰等[24]研究發現行人過街最大等待時間約為40～50 s;馮樹民等[25]得出我國大部分行人過街可容忍的等待時間為50 s。

結合相關研究[15,24-27]和行人等待時間的規律特性能夠發現,行人等待時間與冒險穿越概率之間的關系與生物學中種群增長的S型曲線模型[28]具有極高相似性,因此可對生物學中種群增長模型進行修正,構造概率影響系數,如式(1)所示,可反映行人等待時間對冒險穿越概率的影響。

(1)

式中:ζ為概率影響系數;k為行人心理忍耐極限,可在0～2之間取值,數值越大反映行人越接近心理忍耐極限;k0為行人初始心理感受;r為心理忍耐程度增長率,與行人風格相關;t為行人等待時間。

當行人心理忍耐極限k為2,行人初始心理感受k0為1,概率影響系數ζ隨心理忍耐程度增長率r和行人等待時間t變化的函數圖像如圖1所示。從圖1可以看出,ζ隨著r和t的增大而增大,同時曲率也隨之增大。圖2為當r=25%時概率影響系數ζ函數圖像。從圖2可以看出,冒險概率隨行人等待時間的增加,分為3個明顯不同的階段:1)行人等待時間少于20 s時,冒險穿越概率較低;2)等待20～35 s后,冒險穿越概率迅速增大;3)35 s后冒險穿越概率接近最大。

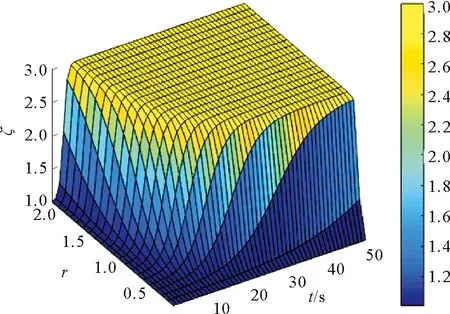
圖1 概率影響系數ζ三維曲面

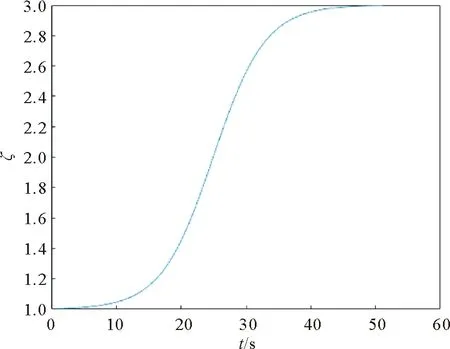
圖2 r=25%時概率影響系數ζ函數圖像

2.2 博弈策略選擇概率

由前文分析可知,行人與車輛在估計自身通行時間和對方通行時間后,通過比較彼此通行時間大小作出決策,因此行人和車輛的策略選擇概率可采用如下方法表示[15]:

(2)

(3)

則行人選擇等待的概率為1-Pp,車輛選擇讓行的概率為1-Pc。

由于上述策略選擇概率僅考慮了行人與車輛對彼此通行時間的判斷過程,無法體現行人等待時間的影響,因此需用Pp與ζ相乘,在博弈中代入修正的行人選擇穿越的概率P′p,即

(4)

2.3 行人緊張度

行人緊張度能反映行人在過街過程中,面對車輛時產生的焦慮情緒,主要表現為在過街過程中的加速、減速、轉向、停止等行為上。

一般情況下,行人緊張度與行人、車間的距離呈負相關,與車輛速度呈正相關,且不同風格的行人面對同一情況下的心理壓力也不同,可通過行人心理壓力場進行衡量,行人心理壓力場場強可表示為

(5)

式中:E為行人心理壓力場場強;εp為風格特性修正系數;ve為速度修正項;tc為車輛反應時間;d為車輛與行人距離;Ls為行人過街安全心理距離;vi為第i車道車輛速度。

行人過街安全心理距離Ls可表示為[29]

Ls=vi(nLc/vp+tp)+Cs

(6)

式中:n為車道數;Lc為車道寬度;vp為行人速度;tp為行人反應時間;Cs為車輛距行人的安全距離。

行人過街時,在其周圍會形成一個如圖3所示以行人為焦點的橢圓形心理壓力場[30],行人受到的心理壓力(反映行人緊張度)與車輛在心理壓力場中所處位置的場強大小、車輛與行人間距和速度以及角度密切相關。橢圓等勢線可表示為

圖3 心理壓力場等勢線

(7)

(8)

(9)

(10)

式中:r為等勢線上的點到行人距離;a為橢圓半長軸;b為橢圓半短軸;c為橢圓半焦距;θ為等勢線上某點和行人連線與行人運動方向所在直線所成的角度;Δt為車輛運動時間。

聯立式(7)—(10)可得:

(11)

當θ=90°,即車輛與行人處于同一車道時,由式(11)可得

d=vi·Δt·(2r+1)

(12)

將式(6)(12)代入式(5)中可得:

(13)

2.4 策略與支付

支付效用函數可反映決策者的收益情況,主要包括延誤、風險、緊張支付,而且與行人風格與車輛駕駛人風格相關,同時還受行人等待時間的影響。設up為行人效用,uc為車輛效用,則二者的支付效用函數可表示為

(14)

(15)

(16)

為了較為直觀地體現不同風格、不同階段下行人與車輛的策略選擇,可設定各類支付效用的初始值,見表2、表3。

表2 行人效用支付

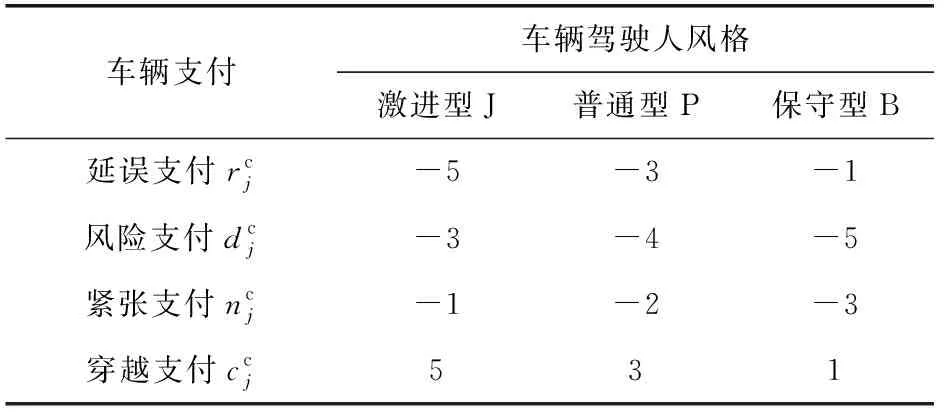
表3 車輛效用支付

對支付效用初始值的設定,分析如下:

1) 根據前文分析,隨著等待時間的變長(即從階段1到階段3),行人冒險穿越概率會增大,因此行人的延誤支付、風險支付的絕對值均增大。由于不同風格行人對延誤和風險的在意程度不同,因此數值設置也有差別。

行人穿越支付為正數,表示獲得通行權的收益,均設定為 1。可理解為,在階段1,行人穿越而機動車避讓的話,行人總的效用支付為:延誤支付+穿越支付,即 1-1=0,行人總支付效用為0,同理,車輛也沒有額外支付,與實際情況相符。

2) 對于車輛來說,車輛并不知道行人處于哪個階段,車輛的決策主要與自身相關,因此根據車輛駕駛人風格不同,合理設定各項支付初始值。

3 博弈模型構建

行人過街與車輛發生沖突后,雙方開始做出的決策往往沒有先后次序,幾乎同時作出決策,因此屬于同時博弈。若在初始階段的博弈達成共識,則博弈結束;若第一階段的博弈無法達成共識,即產生了人車互讓或互不相讓的情況,則會進入下一階段博弈——序貫博弈,在這個階段,沖突雙方會盡可能在揣測對方的意圖后做出決策,并在接下來的行動中進一步修正,直到雙方達成通行共識。

3.1 博弈基本假設

由于行人過街存在諸多的干擾性、不確定性因素,因此在運用博弈理論研究人車沖突問題時需要對博弈雙方以及部分條件進行合理化假設:

1) 將過街行人與車輛視作博弈的雙方,且雙方均為理性人,即雙方的決策都是以實現自身效用最大為目標。

2) 過街行人與車輛彼此互不了解、不清楚對方的行為風格及傾向。

3) 假設過街行人與車輛是在道路、環境條件良好,視距良好的情況下進行博弈。

3.2 混合策略博弈模型

混合策略博弈是指在給定信息情況下,能夠以某種概率選擇不同策略的博弈。行人與車輛博弈的混合策略收益矩陣見表4,行人與車輛選擇不同策略時產生的收益函數為up和uc,例up(C,T)為行人選擇穿越策略且車輛選擇通過策略時行人的收益函數。支付效用注釋見表5。

表4 行人與車輛博弈的混合策略收益矩陣

表5 支付效用注釋

表4中行人和車輛的期望收益可分別表示為

φp=up(C,T)P′pPc+up(C,R)P′p(1-Pc)+up(D,T)(1-P′p)Pc+up(D,R)(1-P′p)(1-Pc)

(17)

φc=uc(C,T)P′pPc+uc(C,R)P′p(1-Pc)+uc(D,T)(1-P′p)Pc+uc(D,R)(1-P′p)(1-Pc)

(18)

通過將式(17)中行人的收益函數φp對Pc求導并令其導數為0,可得P′p為

(19)

同理將車輛的收益函數φc對P′p求導并令其導數為0,可得Pc為

(20)

當博弈中不存在純策略納什均衡,行人和車輛的策略選擇概率P′p和Pc必須滿足上述條件時,才能得到混合策略博弈的納什均衡。

3.3 序貫博弈模型

序貫博弈是博弈雙方選擇策略有時間先后的博弈形式。當行人與車輛在混合策略博弈階段沒有達成共識時,此時進入序貫博弈階段,在該階段分為行人先行和車輛先行兩種情況。

3.3.1 “行人先行”序貫博弈模型

當行人先行動時,車輛會推測行人的行動,然后決定自己的行動,其博弈過程及支付效用,如圖4所示的博弈樹。

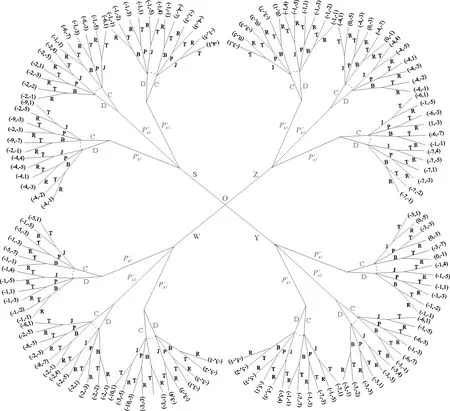
圖4 “行人先行”博弈樹O—博弈樹起點;Z,Y,S,W—支配型、影響型、思考型、穩健型行人;P′p1,P′p2,P′p3—處于行人等待階段1,2,3的概率;C,D—行人穿越和等待;J,P,B—激進型、普通型、保守型車輛駕駛人;T,R—車輛通過和讓行

在該博弈模型中,行人與車輛的博弈過程為:博弈開始時,行人可分為支配型、影響型、思考型、穩健型,4種類型的行人分別以概率P′p1,P′p2,P′p3處于不同等待階段,然后行人進行決策,策略集為{穿越,等待},表示為Sp={C,D};接著3種類型(激進型、普通型、保守型)的車輛駕駛人進行決策,策略集為{通過,讓行},表示為Sc={T,R};最后博弈雙方得到的支付效用結果按照表5所示的函數表達進行計算,結果標注在博弈樹終止節點旁。

由圖4可以看出,Z型(支配型)行人的3個階段中,策略C與策略D帶來的收益相比,0>-1,0>-4,-6>-7;Y型(影響型)行人的3個階段策略C與策略D帶來的收益相比0>-1,-1>-3,-1>-5,因此支配型和影響型行人的策略C屬于占優策略。同理,S型(思考型)行人的階段2和階段3中,策略C與策略D帶來的收益相比-1>-2,-2>-4,因此策略C也屬于占優策略。

當行人的策略確定后,車輛選擇策略T或R取決于車輛的支付效用。

若行人先行動選擇策略C,則機動車選擇策略T的期望收益為

dc=4(P′p1+P′p2+P′p3)Pc(1-3-7)=-36Pc

(21)

若行人先行動選擇策略C,則機動車選擇策略R的期望收益為

dc=4(P′p1+P′p2+P′p3)(1-Pc)(-5-3-1)=-36(1-Pc)

(22)

因此,當Pc>0.5時,若車輛期望收益dc>-36Pc,車輛則選擇策略T;若-36(1-Pc)-36(1-Pc),車輛將選擇策略R。

若行人先行動選擇策略D,則機動車選擇策略T的期望收益為

dc=4(P′p1+P′p2+P′p3)Pc(4+1-2)=12Pc

(23)

若行人先行動選擇策略D,則機動車選擇策略R的期望收益為

dc=4(P′p1+P′p2+P′p3)(1-Pc)(-5-3-1)=-36(1-Pc)

(24)

因此,若車輛期望收益dc>-12Pc,車輛則選擇策略T;若-36(1-Pc)

3.3.2 “車輛先行”序貫博弈模型

當車輛先行動時,行人會推測車輛的行動,然后決定自己的行動,其博弈過程及支付效用,如圖5所示的博弈樹。

圖5 “車輛先行”博弈樹O—博弈樹起點;Z,Y,S,W—支配型、影響型、思考型、穩健型行人;P′p1,P′p2,P′p3—處于行人等待階段1,2,3的概率;C,D—行人穿越和等待;J,P,B—激進型、普通型、保守型車輛駕駛人;T,R—車輛通過和讓行

在該博弈模型中,行人與車輛的博弈過程為:博弈開始時,車輛駕駛人可分為激進型、保守型、普通型,3種類型的車輛駕駛人進行決策,策略集為{通過,讓行},表示為Sc={T,R};然后4種類型(支配型、影響型、思考型、穩健型)的行人分別以概率P′p1,P′p2,P′p3處于不同等待階段,行人進行決策,策略集為{穿越,等待},表示為Sp={C,D};最后博弈雙方得到的支付效用結果按照表5所示的函數表達進行計算,結果標注在博弈樹終止節點旁。

由圖5可以看出,J型(激進型)車輛駕駛人選擇策略T和策略R帶來的收益相比,1和4均大于-5;P型(普通型)車輛駕駛人選擇策略T和策略R帶來的收益相比,1>-3,因此激進型和普通型車輛駕駛人的策略T屬于占優策略。同理,B型(保守型)車輛駕駛人選擇策略T和策略R帶來的收益相比,-2和-7均小于-1,因此策略R屬于占優策略。

當車輛的策略確定后,行人選擇策略C或D取決于行人的支付效用。

若車輛先行動選擇策略T,則行人選擇策略C的期望收益為

dp=3[(-4-3-3-5)PcP′p1+(-6-4-6-8)PcP′p2+(-9-6-7-10)PcP′p3]

=-3Pc(15P′p1+24P′p2+32P′p3)

(25)

若車輛先行動選擇策略T,則行人選擇策略D的期望收益為

dp=3[(-1-1-1-1)Pc(1-P′p1)+(-2-4-3-2)Pc(1-P′p2)

+(-4-7-5-3)Pc(1-P′p3)]=-3Pc[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)]

(26)

因此,當15P′p1+24P′p2+32P′p3>4(1-P′p1)+11(1-P′p2)+19(1-P′p3)時,若行人期望收益dp>-3Pc[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)],車輛則選擇策略D;若-3Pc(15P′p1+24P′p2+32P′p3)

當15P′p1+24P′p2+32P′p3<4(1-P′p1)+11(1-P′p2)+19(1-P′p3)時,若行人期望收益-3Pc[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)]-3Pc(15P′p1+24P′p2+32P′p3),行人將選擇策略C。

若車輛先行動選擇策略R,則行人選擇策略C的期望收益為

dp=3[(-1+0+0-1)(1-Pc)P′p1+(-1+0-1-2)(1-Pc)P′p2

+(-2-1-1-3)(1-Pc)P′p3]=-3(1-Pc)(2P′p1+4P′p2+7P′p3)

(27)

若車輛先行動選擇策略R,則行人選擇策略D的期望收益為

dp=3[(-1-1-1-1)(1-Pc)(1-P′p1)+(-2-4-3-2)(1-Pc)(1-P′p2)

+(-4-7-5-3)(1-Pc)(1-P′p3)]=-3(1-Pc)[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)]

(28)

因此,當2P′p1+4P′p2+7P′p3>4(1-P′p1)+11(1-P′p2)+19(1-P′p3)時,若行人期望收益dp>-3(1-Pc)[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)],車輛則選擇策略D;若-3(1-Pc)(2P′p1+4P′p2+7P′p3)

當2P′p1+4P′p2+7P′p3<4(1-P′p1)+11(1-P′p2)+19(1-P′p3)時,若行人期望收益dp> -3(1-Pc)(2P′p1+4P′p2+7P′p3),車輛則選擇策略C;若-3(1-Pc)[4(1-P′p1)+11(1-P′p2)+19(1-P′p3)]

通過求解博弈模型均衡解的過程可以看出,博弈存在人車沖突的情形(行人選擇策略C,車輛選擇策略T),此種情況下容易造成安全事故和多次博弈。因此,可以通過管理手段和控制手段加以干預,使得行人在選擇策略C(穿越)時,車輛選擇策略T(通過)的支付效用減少而選擇策略R(讓行)帶來的支付效用足夠大,促使車輛選擇策略R,即避讓行人。

同時也存在人車互讓的情形(行人選擇策略D,車輛選擇策略R),此種情況下會造成通行效率低下和多次博弈。因此,可以通過技術手段提高人-車-路的協同程度,在保證安全的情況下,提高通行效率。

4 結論

針對無信號控制場景下,行人過街過程中行人與車輛存在沖突的現狀,基于博弈論,分析了人車沖突過程中的決策行為。通過對行人過街過程進行分析,能夠發現行人與車輛的博弈過程受多因素影響,包括行人等待時間、策略選擇概率、行人緊張度、策略支付,同時也將延誤、風險度、行人風格和車輛駕駛人風格等融合考慮。通過將上述多因素進行綜合分析,合理確定了支付效用函數以及支付效用初始值,并根據人車博弈過程構建了3類博弈模型,即混合策略博弈模型、“行人先行”序貫博弈模型和“車輛先行”序貫博弈模型。

通過分析上述3類博弈模型的納什均衡解和不同情況下博弈雙方(行人和車輛)的收益,描述了行人過街和車輛之間的決策行為過程,得到了收益區間與策略選擇的關系,得出了行人和車輛在不同情況下的占優策略和策略選擇情況。研究結果表明:不同風格的行人和車輛駕駛人,在不同階段、不同行動順序下決策收益不同,占優策略存在差異。分析人-車沖突的決策過程和決策影響因素對于揭示人-車沖突機理,減少人-車沖突事故具有重要意義。