一維熱傳導方程數值解的計算機仿真與研究

斯小琴,陳大偉,岳生偉

(1.安徽建筑大學 城市建設學院,合肥 238076;2.中國科學技術大學 物理學院,合肥 230026)

熱傳導(thermal conduction)實質是由于物體內部大量分子熱運動相撞擊使溫度分布不均勻,即物體內存在溫度差,熱量要從物體溫度較高的點流向溫度較低的點[1-2]。熱傳導過程是一個基礎性的物理過程,其數學模型在實際應用中非常廣泛[3-7],如光學研究、航天科學技術、地質勘測、水利工程、工業制造等諸多領域。因此,對熱傳導的研究越來越受到人們的重視。

熱傳導過程通常用偏微分方程表示,借助數學模型來描述物體上各點的溫度分布和變化具有重要的意義。對這種偏微分方程進行研究有助于對熱傳導過程基本規律的更深理解,以便用來更好的解決實際問題[8-9]。而對于各種定解條件下的熱傳導方程的求解更是一個熱點問題。雖然科研工作者們已經提出了一些求解其解析解的方法[10-12],但這些獲得的解只對少量的簡單情形適用,對于那些具有實際物理意義的復雜的熱傳導問題,其精確解往往很難得到,這時使用數值解方法來求解就顯得尤為重要[13-14]。

求解熱傳導問題數值解方法很多,最常用的方法有有限差分法、有限元法和邊界元法。差分法[15]劃分的網格是規則的,具有形式簡單、使用方便的優點,但對計算條件要求高;有限元法[16]網格劃分則較靈活,對于不規則區域和彎曲邊界可方便的處理,但需要求解大規模線性代數方程,這將消耗過長的計算時間和占用較大的CPU存儲空間;邊界元法[17]用簡單的網格準確模擬邊界形狀,得到線性代數方程組的階數較低,具有較高的精度,但難以應用于非均勻介質問題。

本文利用最常用的較成熟、應用廣的有限差分法,借助基本辦公軟件Excel迭代[18-19],通過Origin將迭代的數據模擬成圖形,得到了含初始和邊界條件的混合問題的一維熱傳導方程的溫度隨時空變化圖,以及數值解與精確解的誤差比較。從圖像中觀察物體上各點的溫度隨時間和空間的分布狀態。將簡單、靈活、精度高、通用性強的有限差分法與基本辦公軟件Excel的迭代計算功能相結合,避免了求解繁瑣的熱傳導方程以及復雜的計算機編程,給解決實際問題帶來了方便。進一步通過Origin將數值模擬成圖形,結果直觀、形象。

1 模型與方法

長度為1 m的勻質熱導體,其兩端的溫度均為0 ℃且保持溫度不變,初始時刻溫度分布為u(x,0)=sinπx,考察該熱導體上溫度的分布情況。則其熱傳導方程表示如下:

(1)

其中u(x,t)表示導熱體上t時刻x處的溫度,該方程的精確解為

u(x,t)=e′-π2tsinπx

通過有限差分法求方程(1)的數值解。現將溫度u(x,t)在節點(x,t)處沿x向前h、向后h以及沿t向前τ進行Taylor展開,有

(2)

(3)

(4)

由式(2)+(3)并略去高階項,得

(5)

由式(4)略去高階項,得

(6)

將式(5)(6)代入式(1),有

(7)

以時間步長τ=0.15/m和空間步長h=1/n(m,n為自然數)分別將時間[0,0.15]和空間[0,1]進行離散化,可以將一維的時空平面劃分成一個m×n的網格面,各個網格點則表示所對應的時空溫度。得到式(1)熱傳導問題的離散網格分別表示如下:

(8)

則由式(7)可得一維差分方程為

(9)

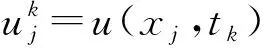
引入步長比r=τ/h2,則式(9)可改寫為

(10)

2 數值模擬結果及分析

現取不同的步長,考察τ和h取值不同,其對數值解精度高低的影響。在基本辦公軟件Excel中第一行表示空間節點,第一列表示時間節點,分別代入式(1)中的初始和邊界條件,再編入式(10)的差分公式,利用其迭代計算很快計算出各時刻在每個位置的溫度值。改變步長,溫度值隨之改變。將得到的數值解與精確解進行比較,計算出兩解差的絕對值,通過MAX函數得到其最大誤差。表1列出了部分最大誤差數值,固定空間步長h=0.05 m不變,改變時間步長。步長改變,其步長比r緊跟改變,從表1中可以看出,步長比越小,數值解的精度越高,也就是說,所取得步長越小,精度越高,這些前提是要步長比r≤1/2。

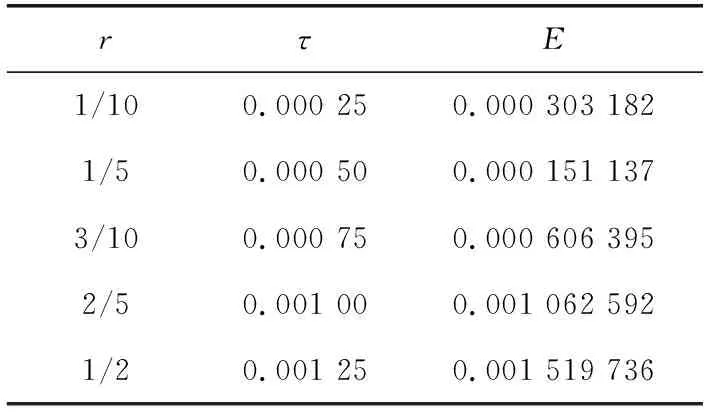
表1 不同步長比時數值解的最大誤差

下面在此方法穩定的條件下以最大步長比即r=1/2討論相關問題。若分別取空間步長h=0.05和時間步長τ=0.001 25,通過Excel計算出數值解和精確解數值及兩解差的絕對值。表2 列出了其數值解、精確解及兩解差的絕對值在部分節點處的數值。

表2 部分節點處數值解、精確解及兩種解的差的絕對值

為了直觀、形象地觀察和理解熱導體上熱量分布隨時間、空間的變化規律,通過Origin畫圖軟件將計算出的數值模擬成圖形。圖1是h=0.05和τ=0.001 25的溫度隨時間和空間變化的數值解圖。從圖1中很直觀地看出,在x=0時溫度為0 ℃,隨著位置的變化,溫度先增大隨后減小,直到導熱體的另一端溫度又減小到0 ℃,即該端點處與外界絕熱,圖形與理論基本相吻合,從圖形中觀察更直觀。

圖1 導熱體上的溫度隨時間、空間變化分布

通過數值解與精確解進行對比,更好地說明了此方法在精度范圍內的可行性。圖2是數值解和精確解誤差曲面圖。從圖2中可看出,誤差值很小,基本都在0.001即0.1%之內。沿著x方向向前看,誤差值先增后減;沿著t方向向前看,誤差值先急劇增加后趨于平緩。

圖2 數值解與精確解誤差曲面

圖3和圖4是圖2的剖析圖,分別考察了誤差值與位置x和時間t的關系。圖3是取空間步長h=0.05和時間步長τ=0.001 25,當位置控制在x=0.6 m時的誤差隨時間變化的曲線。從圖3中可以看出,開始時誤差增加的較大而后趨于平緩甚至最后有減小的趨勢,與圖2中觀察到的基本一致。

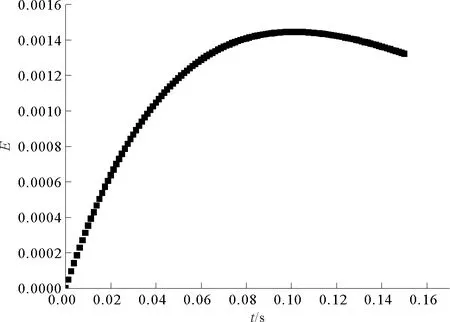
圖3 誤差隨時間變化的曲線

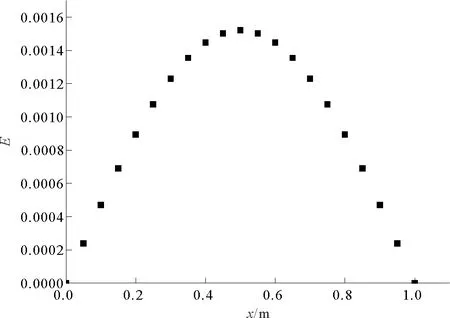
圖4 誤差隨空間位置變化的曲線

圖4是取空間步長h=0.05和時間步長τ=0.001 25,當時間控制在t=0.1 s時的誤差隨空間位置變化的曲線。從圖4中可知,在兩端點處因都保持0 ℃不變,誤差值均為0,隨后誤差值先增加后減小,出現對稱分布狀態,與圖2中的相吻合。

3 結論

本文通過有限差分法的差分格式得到了一維熱傳導方程的數值解,將其初始、邊界條件及數值解的差分格公式編入基本辦公軟件Excel中,通過其下拉迭代計算功能,快速地得到了熱傳導方程每個網格點的溫度值。借助Origin將計算出的大量數據繪制成圖,并與精確解進行對比,得到了數值解與精確解的誤差曲面圖。從圖形中觀察結果更加直觀、形象。該方法對于不同初始、邊界條件下或有非齊次項f(x,t)的熱傳導方程的求解同樣適用。對解決實際問題帶來了方便并有一定的參考價值。