一步優化OSAHS 鼾聲分類算法

余佳琪， 王冬霞， 馬曉冬， 張 嚴

（1.遼寧工業大學電子與信息工程學院，遼寧 錦州 121001；2.大連凡益科技有限公司，遼寧 大連 116033）

0 引言

阻塞性睡眠呼吸暫停低通氣綜合征（Obstructive Sleep Apnea-Hypopnea Syndrome，OSAHS）嚴重危害患者身體健康，鼾聲的檢測與分類作為診斷OSAHS的重要標志，已成為現階段的研究熱點。醫院通過多導睡眠圖（Polysomnography，PSG）對OSAHS 進行診斷。PSG法成本較高，不具備普適性。就此，提出一種簡潔、高效的鼾聲分類算法應用于臨床診斷。

現階段常采用人工切割標注［1-3］，即分別通過人耳和PSG數據對齊的方式對整夜錄音進行切割標注，復雜度較高，且易出現遺漏［4-5］。研究人員采用多階段法對鼾聲進行檢測與分類，即有聲段檢測［6-7］、特征提取［8-9］和鼾聲分類。鼾聲分類方法的研究，主要采用兩步分類實現［10］鼾聲/非鼾聲分類［11］、OSAHS患者鼾聲/正常鼾聲分類［8］。兩步分類法過程復雜且計算量大。Luo 等［2］利用時域卷積網絡（Temporal Convolutional Network，TCN）模型對患者鼾聲、正常鼾聲和非鼾聲進行一步分類，準確率可達96.3%，但所選非鼾聲數據集為理想集，不具備普適性。為解決上述問題，提出一步切割聚類的鼾聲分類算法（BICVAD-CART-LDA algorithm，BVCL），以實現OSAHS 的輔助篩查。

1 BVCL鼾聲分類算法

本文所用臨床夜間實錄鼾聲數據包含OSAHS 患者鼾聲、正常鼾聲和非鼾聲等多種聲音。為實現復雜環境下實錄鼾聲的檢測與分類，提出了一種BVCL 鼾聲分類算法。

1.1 BV算法

1.1.1 BIC檢測

切割點的檢測［12-13］可視為統計學上的模型選擇問題，通常以貝葉斯信息準則（Bayesian Information Criterion，BIC）作為判定標準，一般選擇BIC 值小的模型。

將實錄鼾聲信號的特征序列建模成獨立多元高斯過程xi～N（μi，Σi），其中xi∈Rd，i=1，2，…，N。提取實錄鼾聲的梅爾頻率倒譜系數（Mel-Frequency Cepstral Coefficient，MFCC）特征，xi作為從實錄鼾聲音頻流中提取的特征向量序列，其中d為特征向量維數，N是特征向量個數。μi和Σi分別為xi的均值向量和協方差矩陣。

假設一段鼾聲音頻在第i時刻有一個跳變點，尋找跳變點可看作對模型H1：x1…xi～N（μ1，Σ1）；xi+1…xN～N（μ2，Σ2）和模型H0：x1…xN～N（μ，Σ）進行選擇的問題。

若存在跳變點，則模型H1的對數最大似然比

式中：N=N1+N2，N1和Σ1分別是｛x1…xi｝的特征向量個數和協方差矩陣，N2和Σ2分別是｛xi+1…xN｝的特征向量個數和協方差矩陣，“”為矩陣Σ的行列式。

因此，跳變點的最大似然估計

比較兩個模型，H1將xi建模為兩個高斯過程，H0將xi建模為一個高斯過程。這兩個模型的BIC 值之差

式中：P=0.5［d+0.5d（d+1）］lnN為懲罰項；λ為懲罰項權重，一般取1。

因此，若式（3）為正，則采用2 個高斯過程的模型H1，即存在一個跳變點。所以，則表示此時有兩個獨立的鼾聲音頻分段，存在一個切割點；反之，，則表示此時只有一個獨立的鼾聲音頻分段，沒有切割點。

上述方法僅對鼾聲進行單切割點檢測，進一步提出一種多切割點BIC檢測算法：設置一個檢測窗口，通過BIC檢測算法判斷在當前窗口范圍內是否存在切割點，若存在切割點，則該窗口繼續移動，且窗口大小不進行調整；反之，則調整窗口的上限。重復上述過程直至檢測窗口的上限超出整段音頻的終點。

1.1.2 VAD檢測

語音端點檢測（Voice Activity Detection，VAD）算法［12］常用短時能量（Short Time Energy，STE）和短時過零率（Zero Crossing Rate，ZCR）判別語音信號和非語音信號。信噪比較大時，STE ＞ZCR，而非語音信號的STE ＜ZCR。因此，可利用STE 和ZCR的大小直接判別語音信號和非語音信號。

為解決起始帶噪靜音段終止點無效切割，提出利用VAD 技術快速篩選無效切割點。利用多切割點檢測算法對處理后的切割點進行音頻分段和VAD檢測，若檢測有語音端點，則不處理；反之，則剔除該切割點。

1.1.3 BIC聚類

切割后的實錄鼾聲音頻片段還需進行標注，才能用于后續的分類訓練。基于此，為提高標注效率，提出實錄鼾聲的BIC聚類算法。

假設S=｛si：i=1，2，…，M｝為切割后實錄鼾聲音頻片段的集合；χi=為從第i段提取的MFCC特征向量；為MFCC特征向量χi的總樣本大小；=｛ci：i=1，2，…，k｝為有k個簇的聚類，把每個簇ci看作是一個多元的高斯分布ci～N（μi，Σi）。每個簇的參數數量為d+0.5d（d+1），ni是簇ci中的樣本數。由前文BIC算法原理可知：

以切割后的實錄鼾聲信號為節點，依據距離度量連續合并2 個最近的節點。S=｛s1，s2，…，sk｝是當前的節點集；s1、s2是候選的一對合并節點，合并后的新節點是s。將當前的聚類S與新的聚類S′=｛s，s3，…，sk｝進行比較。將每個節點si建模為多元高斯分布N（μi，Σi）。由式（4）可見，通過合并s1、s2，BIC值

式中：n=n1+n2為合并節點的樣本數量；Σ是合并節點的樣本協方差矩陣。若式（5）為負，則2 個節點不合并。

采用式（5）作為BIC 的距離度量，同時利用節點的MFCC特征作為初始點，遍歷其余節點，計算每個節點與初始點間的BIC 距離。設置BIC 距離閾值，確定該段是否與初始點位于同一類簇中，實現OSAHS患者鼾聲、正常鼾聲和非鼾聲的聚類，輸出帶標簽的數據集送入分類算法（CART-LDA algorithm，CL）。

1.2 CL算法

1.2.1 CART模型

就分類而言，盡可能選擇“純度”最高的特征讓劃分后的樣本都屬于同一類。基尼系數（Gini）作為判別數據“純度”的指標，在大數據量問題上，具有運行速度快的優勢。

分類回歸樹（Classification and Regression Tree，CART）是以最小Gini 系數來選擇最優特征并構建二叉樹的分類模型。經切割聚類算法（BIC-VAD algorithm，BV）處理后的實錄鼾聲數據集為D，若從中提取的特征為F，以特征F作為劃分指標，將數據集D劃分為兩部分D1和D2，則在特征F條件下的Gini 系數為：

式中：Di為Dk部分第i類的樣本；C為實錄鼾聲所含類別數。

1.2.2 CL分類

經過CART模型特征選擇后的最優特征集中包含MFCC等高維度特征，算法的維數與復雜度呈指數級增漲；同時，現階段兩步分類法［8，11］過程復雜且一步分類法［2］準確率不高。基于此，提出實錄鼾聲的CL 分類算法，既保留CART模型計算速度快，并且使用Gini系數能有效選擇最優特征的優點，還引入線性判別分析（Linear Discriminant Analysis，LDA）算法［14］進行特征降維，節約模型訓練時間，去除數據冗余，提高算法的分類準確率。

LDA算法是通過投影的方式去除數據之間冗余。假設有兩類數據（OSAHS患者鼾聲和正常鼾聲），實錄鼾聲樣本xi∈Rd，其中維數d=2；所有類別為ci的樣本集。所有鼾聲數據xi投影到單位向量ω后，其均值為

式中：ai為xi在單位向量ω上的偏移或者坐標，表示做了一個映射Rd→R，即通過投影將d維向量降到一維；μ1和n1分別為樣本集D1的均值向量和樣本數。同理，樣本集D2的均值向量μ2，投影后的均值m2=ωTμ2。為使投影后的鼾聲數據能準確分類，這兩類鼾聲數據的中心距離越遠越好，即要使m1-m2最大。但該條件不能保證能正確地對每一個數據進行分類，還需考慮每一類數據的方差，方差大表示兩類數據之間有重疊，方差小表示無重疊。

LDA算法未采用方差，而采用散布矩陣

式中：

對式（10）求導，得：

式中，令λ=J（ω），λ為常量。

LDA算法僅適合二分類問題，為實現OSAHS 患者鼾聲、正常鼾聲和非鼾聲的3 分類，對上述算法進行改進，即可計算S-1B對應的最大特征值的特征向量。

式中：μ為整個實錄鼾聲樣本的均值向量；ni、μi分別為第i類中樣本個數和均值向量。

CL分類算法的基本思想：利用CART模型進行最優特征選擇；計算每一類的協方差矩陣Si，i=1，2，3，并計算S-1B的特征向量Q=［ω1，ω2，…，ωd］，其中ω1，ω2，…，ωd對應的特征值滿足λ1≥λ2≥…≥λd，矩陣W=［ω1，ω2，…，ωk］由Q中前k個特征向量組成，其中k＜d；對原實錄鼾聲數據X進行投影：

式中：X為原始數據集；Y為將X向子空間W =span｛ω1，ω2，…，ωk｝投影后得到的分類后的數據集。

1.3 BVCL算法

圖1 為BVCL算法流程。將臨床夜間實錄鼾聲作為輸入，經分幀加窗處理后，從音頻信息中提取MFCC特征，通過BIC 檢測算法實現多切割點檢測；利用VAD檢測算法篩選無效切割點；通過BIC 聚類算法將切割后的片段進行聚類，輸出帶標簽的數據集送入CL算法，從音頻信息中提取MFCC、頻譜帶寬、色度頻率等26 個特征，對OSAHS患者鼾聲、正常鼾聲和非鼾聲進行一步分類。

圖1 BVCL算法流程

2 仿真結果與分析

為驗證所提算法的有效性，以某醫科大學附屬醫院整夜實錄鼾聲數據作為輸入，對OSAHS 患者鼾聲、正常鼾聲和非鼾聲進行切割聚類和分類，并利用k折交叉驗證［15］（k= 10）和受試者工作特征（Receiver Operating Characteristic，ROC）曲線來評估分類模型的性能。

2.1 實驗參數設置

實驗數據包含13 例OSAHS患者和6 例正常打鼾者。采用PSG 監測系統監測受試者整晚（約9 h）的PSG信號，同時將麥克風放置在距離受試者口鼻之上約45 cm處，以8 kHz的采樣頻率和16 bit采樣精度采集聲信號后保存于錄音機中，獲得原始睡眠鼾聲信號。

鑒于整夜實錄鼾聲較長，將其分成15 min 文件長度進行處理。利用BVCL算法從實錄鼾聲信號中提取有聲段進行切割聚類，共計23897 個聲音片段，作為分類階段的樣本集。從這些帶標簽的片段中提取MFCC、頻譜帶寬、色度頻率等26 個特征作為訓練對象，從樣本集中隨機抽取19118 個樣本（約占總數據的4/5）作為訓練集，其余4779 個樣本作為測試集，進行算法模型的訓練和測試。

2.2 仿真結果

（1）驗證算法切割聚類性能。為驗證BVCL算法的快速切割聚類能力，表1 為相應的仿真結果。

表1 切割聚類仿真結果

結果表明，將BVCL 算法切割后的聲音片段與經由專業人員標注后的片段進行比較，BVCL 算法的平均準確率為98.99%，能有效從實錄鼾聲信號中切割聚類出OSAHS患者鼾聲、正常鼾聲和非鼾聲。與人工切割標注法［1-3］相比，未用算法之前人工需要45.38 h，使用該算法后只需6.75 h，時間節省了38.63 h，為快速檢測鼾聲提供了前提，且準確率提高了3.32%。切割聚類后輸出帶標簽的數據集，經人工修正至100%準確率后，作為分類模型的輸入集。

（2）驗證算法分類性能。為驗證BVCL算法的分類效果，選取切割后片段80%為訓練集，20%為測試集。圖2 所示為算法分類結果。

圖2 BVCL算法分類結果

如圖2 所示，在臨床復雜環境下，BVCL 算法的分類準確率可達99.15%，且具有較強的抗干擾能力。

k折交叉驗證能有效解決過擬合與欠擬合的不足，且可靠性較高。利用k折交叉驗證（k=10）驗證BVCL算法分類性能。將樣本隨機均勻分為k組，每組數據分別作為一次測試集，其余k-1 組作為訓練集。采用平均分類準確率作為分類模型的評價指標。圖3所示為k折交叉驗證結果。

圖3 k折交叉驗證結果（k=10）

由圖3 可見，BVCL 算法的平均分類準確率為99.02%，極差為0.24%，具有較強的魯棒性。圖4 所示為CART、LDA和BVCL算法的ROC 曲線。ROC 曲線下面積為AUC（Area Under Curve），AUC 的取值范圍一般為0.5 ～1.0，AUC越接近1.0，分類效果越好。

圖4 ROC曲線

由圖4（a）可知，采用CART 模型分類的AUC 為0.919；由圖4（b）可知，采用LDA 算法分類的AUC 為0.888；而采用BVCL算法分類的AUC為0.990。結果表明，BVCL算法的分類效果更好。

（3）算法對比。所提BVCL算法將兩步分類過程簡化為一步，與文獻［8，11］中的算法相比分類準確率提高了4.08%；與文獻［2］中的一步分類法相比，論文所用數據均來自臨床夜間實錄，更具普適性，且分類準確率提高了2.85%。圖5所示為各算法仿真結果對比。

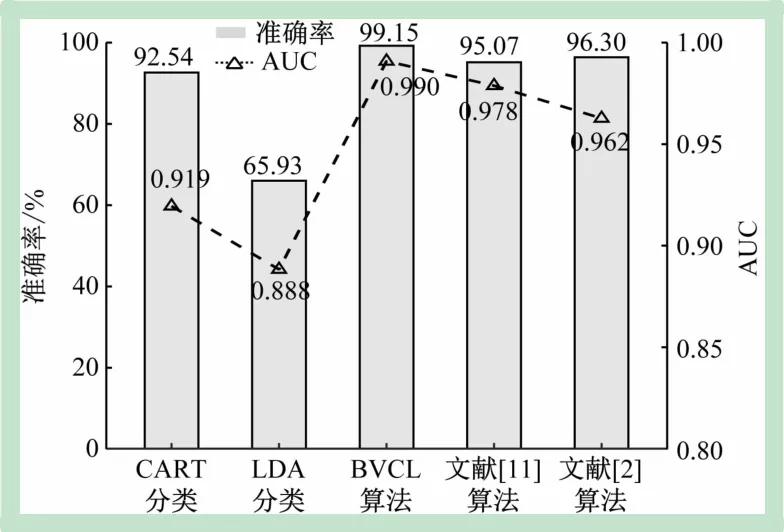
圖5 各算法仿真結果對比

如圖5 所示，BVCL算法的分類準確率和AUC 均優于對比的算法。結果表明，BVCL 算法的準確率和分類效果均有提升。

綜上，在臨床復雜環境下，BVCL算法的準確率可達99.15%，且分類效果更好，能快速實現OSAHS 患者的輔助篩查。

3 結語

由于臨床診斷OSAHS 費用昂貴、操作復雜，尋找一種低成本、易于操作的方法來輔助篩查OSAHS具有廣闊的前景。考慮到臨床實測環境復雜導致OSAHS鼾聲檢測準確率不高，提出一步切割聚類的鼾聲分類算法（BVCL）。仿真表明，該算法在大量數據快速切割聚類以及OSAHS檢測分類方面具有良好的性能，為便攜式睡眠鼾聲監測設備走向實際提供一種快速實現的手段。未來將繼續優化算法針對低信噪比環境下的分類性能，同時提取并篩選更多分類效果好的特征。