改進(jìn)自抗擾下的細(xì)紗機(jī)卷繞系統(tǒng)控制策略

廉繼紅,王炳炎,王延年,王 棟

(西安工程大學(xué) 電子信息學(xué)院,陜西 西安 710048)

0 引 言

細(xì)紗是紡紗過程的重要工序,它將粗紗紡制成細(xì)紗并卷繞于筒管之上制成管紗。卷繞過程的好壞對(duì)管紗質(zhì)量和成品率有著非常重要的影響[1]。由于在卷繞細(xì)紗的過程中,紗線上的張力是不斷變化的,永磁同步電機(jī)需要隨著卷繞過程的進(jìn)行不斷調(diào)速,而調(diào)速過程中,永磁同步電機(jī)的轉(zhuǎn)速、轉(zhuǎn)矩就會(huì)產(chǎn)生劇烈波動(dòng),此時(shí)極易出現(xiàn)紗線斷頭的現(xiàn)象[2]。而永磁同步電機(jī)先進(jìn)控制策略被越來越多地用來解決以上問題[3-4]。

近年來,國(guó)內(nèi)外學(xué)者提出了許多先進(jìn)的控制策略,常見的有廣義預(yù)測(cè)PID控制算法與滑模自抗擾控制算法[5-6]。廣義預(yù)測(cè)PID控制算法中,利用廣義預(yù)測(cè)算法對(duì)PID參數(shù)進(jìn)行整定,但預(yù)測(cè)精度不高,存在誤差較大。傳統(tǒng)的滑模自抗擾控制算法中,擴(kuò)張狀態(tài)觀測(cè)器的初始峰值問題沒有得到解決,且滑模控制存在一個(gè)不可避免的問題,即在系統(tǒng)運(yùn)行至滑模面后,無法嚴(yán)密沿著滑模面朝穩(wěn)定點(diǎn)的方向運(yùn)動(dòng),從而形成高頻抖振。

為此,本文提出了改進(jìn)GWO算法下的基于增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器與改進(jìn)型趨近率滑模控制聯(lián)合改進(jìn)的自抗擾控制策略。首先采用基于增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器的改進(jìn)自抗擾控制方法,降低了傳統(tǒng)擴(kuò)張狀態(tài)觀測(cè)器中的初始峰值,提高了觀測(cè)精度[7]。其次利用改進(jìn)型趨近率滑模控制代替自抗擾中的狀態(tài)誤差反饋控制器,由于可變參數(shù)較多,同時(shí)采用改進(jìn)GWO算法對(duì)控制參數(shù)進(jìn)行調(diào)節(jié),提高了參數(shù)的精確度,不僅提高了滑模控制器的收斂速度,也降低了高頻抖振。最后通過仿真驗(yàn)證表明本文提出的控制策略驅(qū)動(dòng)永磁同步電機(jī),能有效提高電機(jī)調(diào)速性能,提高管紗質(zhì)量,且能降低系統(tǒng)的波動(dòng),防止細(xì)紗斷頭。

1 系統(tǒng)建模

細(xì)紗卷繞是將成品細(xì)紗制成管紗的關(guān)鍵步驟,卷繞系統(tǒng)的關(guān)鍵部分是帶動(dòng)筒管轉(zhuǎn)動(dòng)的永磁同步電機(jī)。以下對(duì)卷繞系統(tǒng)和永磁同步電機(jī)進(jìn)行建模。

1.1 細(xì)紗機(jī)卷繞系統(tǒng)建模

從圖1可以看出,粗紗經(jīng)過導(dǎo)紗桿從粗紗管上退繞下來,立刻被導(dǎo)紗桿導(dǎo)入橫動(dòng)裝置,經(jīng)橫動(dòng)裝置喂給紗線到牽伸裝置,牽伸裝置會(huì)將喂入的須條均勻牽伸,使得紗線達(dá)到所需要的特?cái)?shù)。牽伸完成后由導(dǎo)紗鉤牽引紗線到鋼領(lǐng)板上進(jìn)行加捻[8],最后將加捻后的紗線進(jìn)行卷繞,使紗線成型規(guī)律、緊密一致地卷繞在紗筒上,便于后續(xù)加工使用。

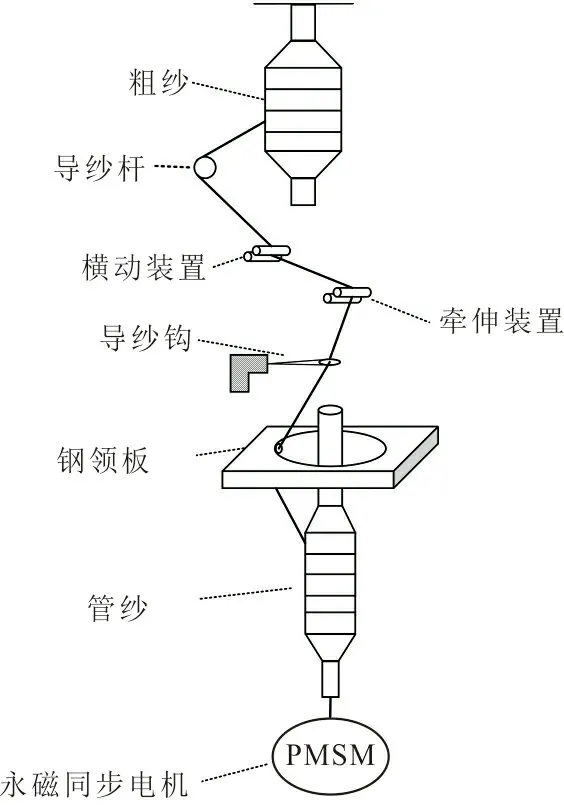
圖1 細(xì)紗機(jī)卷繞系統(tǒng)原理Fig.1 Schematic of spinning frame winding system

圖2 常規(guī)趨近率性能Fig.2 Conventional approaching rate

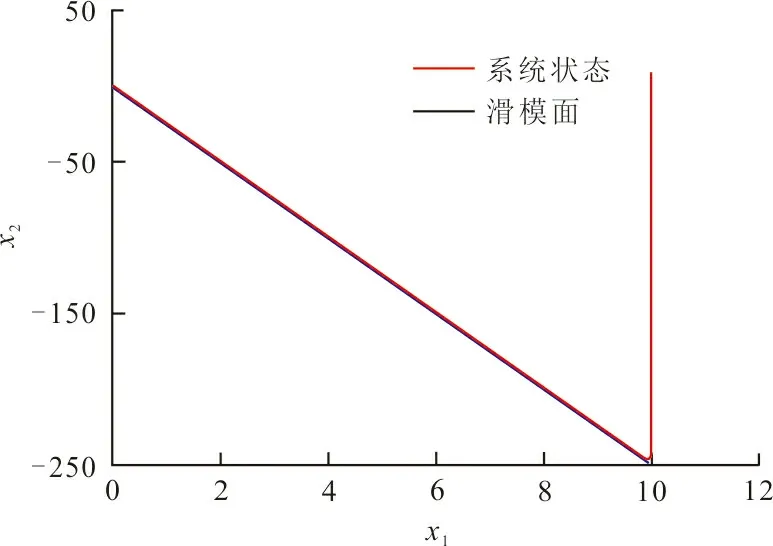
圖3 改進(jìn)趨近率性能Fig.3 Improved approaching rate ability

在細(xì)紗卷繞過程中,永磁同步電機(jī)用來控制紗錠的運(yùn)動(dòng),根據(jù)卷繞系統(tǒng)模型和卷紗幾何規(guī)律可知：

式中：v為紗線卷繞線速度;vr為往復(fù)導(dǎo)紗速度;h為法相螺距;rk為紗筒的卷繞半徑。

卷繞半徑rk可表示為

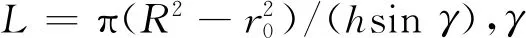
由式(2)可得,導(dǎo)紗機(jī)構(gòu)運(yùn)動(dòng)速度可表示為

1.2 永磁同步電機(jī)的數(shù)學(xué)模型

永磁同步電機(jī)是一種復(fù)雜的非線性系統(tǒng),內(nèi)部轉(zhuǎn)子和三相繞組之間相互作用存在耦合,為了便于分析各個(gè)參數(shù)之間關(guān)系,假設(shè)：

1) 內(nèi)部鐵芯不存在飽和的情況;

2) 不需要考慮電機(jī)內(nèi)部渦流的損耗;

3) 轉(zhuǎn)子和永磁體無阻尼。

永磁同步電機(jī)三相靜止坐標(biāo)系abc下的電壓方程為

式中：ua、ub、uc為三相電壓;ia、ib、ic為三相電流;Rs為轉(zhuǎn)子電阻;φa、φb、φc為三相磁鏈。

為了簡(jiǎn)化計(jì)算,將三相靜止坐標(biāo)系abc轉(zhuǎn)化為兩相dq坐標(biāo)系[9],則電壓方程為

式中：id和iq為定子電流;ud和uq為定子電壓;Ld和Lq為定子電感;φf為永磁體磁鏈;R為定子電阻;ωe為轉(zhuǎn)子角速度。則永磁同步電機(jī)運(yùn)動(dòng)方程為

式中：B為黏滯摩擦系數(shù);p為極對(duì)數(shù);J為轉(zhuǎn)動(dòng)慣量;ω為實(shí)際機(jī)械角速度;TL為負(fù)載轉(zhuǎn)矩。最終得到永磁同步電機(jī)轉(zhuǎn)矩方程為

2 永磁同步電機(jī)改進(jìn)自抗擾控制器

2.1 自抗擾控制系統(tǒng)設(shè)計(jì)

自抗擾控制是一種無模型且魯棒性強(qiáng)的非線性控制方法,因其靈活性高被廣泛應(yīng)用于工業(yè)控制中。自抗擾控制器由跟蹤微分器、擴(kuò)張狀態(tài)觀測(cè)器及狀態(tài)誤差反饋控制器組成[10]。其中,跟蹤微分器的作用就是將輸入進(jìn)來的信號(hào)經(jīng)過處理,輸出2類信號(hào);擴(kuò)張狀態(tài)觀測(cè)器將影響輸出的擾動(dòng)擴(kuò)張為新的狀態(tài)觀測(cè)變量,準(zhǔn)確地觀測(cè)擴(kuò)張后的總擾動(dòng)量,并對(duì)其進(jìn)行自動(dòng)補(bǔ)償;狀態(tài)誤差反饋控制器則是將跟蹤微分器的過渡量和擴(kuò)張狀態(tài)觀測(cè)器的狀態(tài)估計(jì)量?jī)烧叩钠钸M(jìn)行組合,并對(duì)整個(gè)控制系統(tǒng)作出有效補(bǔ)償[11-12]。

由于永磁同步電機(jī)速度控制是一階的,不需要二階變量,為了簡(jiǎn)化設(shè)計(jì),舍棄跟蹤微分器。

在擴(kuò)張狀態(tài)觀測(cè)器中,fal是一個(gè)非線性函數(shù),用于消除系統(tǒng)擴(kuò)張了一個(gè)狀態(tài)后產(chǎn)生的未知函數(shù)對(duì)系統(tǒng)的影響,表達(dá)式為

式中：e為輸入誤差變量;α為非線性系數(shù)且0<α<1,δ為濾波系數(shù)。

擴(kuò)張狀態(tài)觀測(cè)器在設(shè)計(jì)過程中,僅設(shè)計(jì)合適的增益系數(shù)就可以實(shí)現(xiàn)對(duì)系統(tǒng)總擾動(dòng)精準(zhǔn)觀測(cè)[13-14]。但傳統(tǒng)fal函數(shù)是不連續(xù)函數(shù),此函數(shù)在不連續(xù)點(diǎn)的切換會(huì)使得動(dòng)態(tài)增益出現(xiàn)波動(dòng),容易出現(xiàn)觀測(cè)量抖振的問題。因此提出增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器對(duì)系統(tǒng)的擾動(dòng)進(jìn)行觀測(cè)[15-16]。

首先定義一個(gè)具有連續(xù)可導(dǎo)特性的誤差矯正函數(shù)：

式中：λ為誤差增益。本文選取α=0.5,λ=5 000,由于傳統(tǒng)擴(kuò)張狀態(tài)觀測(cè)器在增益參數(shù)較大時(shí),會(huì)導(dǎo)致擴(kuò)張狀態(tài)觀測(cè)器的初始狀態(tài)z1與系統(tǒng)的初始狀態(tài)ω之間的誤差較大,且估計(jì)值z(mì)2對(duì)總擾動(dòng)f的跟蹤不準(zhǔn)確,容易產(chǎn)生峰值問題。因此,本文提出的可調(diào)增益狀態(tài)觀測(cè)器[17-18]可表示為

式中：β1、β2是誤差矯正因子;r(t)為變?cè)鲆?b0為補(bǔ)償因子;e1為初始狀態(tài)誤差。狀態(tài)誤差反饋控制器可設(shè)計(jì)為

式中：e2為輸出狀態(tài)誤差;ω*為期望角速度;β3為誤差矯正因子。

2.2 滑模自抗擾控制系統(tǒng)設(shè)計(jì)

上述方法解決了傳統(tǒng)擴(kuò)張狀態(tài)觀測(cè)器中的峰值問題。速度誤差經(jīng)過狀態(tài)誤差反饋控制器的輸出精度略微提高,但該控制器應(yīng)用于紗線卷繞系統(tǒng)中魯棒性有待提高。

滑模控制具有響應(yīng)速度快、魯棒性強(qiáng)、可靠性高等特點(diǎn)[19],但是在系統(tǒng)達(dá)到穩(wěn)態(tài)時(shí)會(huì)有抖振的產(chǎn)生,而自抗擾控制方法中的擴(kuò)張狀態(tài)觀測(cè)器能夠有效的觀測(cè)系統(tǒng)受到的不確定擾動(dòng),并在反饋中對(duì)系統(tǒng)的擾動(dòng)值進(jìn)行補(bǔ)償。滑模控制中存在的抖振問題可以利用自抗擾控制中的擴(kuò)張狀態(tài)觀測(cè)器進(jìn)行消除[20-21],因此,本文提出用改進(jìn)滑模控制代替狀態(tài)誤差反饋控制環(huán)節(jié),設(shè)計(jì)自抗擾控制與滑模控制相結(jié)合的改進(jìn)型趨近律的滑模自抗擾控制器。

本文利用積分型滑模面表達(dá)式如下：

式中：c為大于零的變量;e0為跟蹤誤差,e0=ω*-ω。為了提高趨近階段的動(dòng)態(tài)質(zhì)量,本文使用改進(jìn)型趨近率：

式中：σ、K、η為增益系數(shù)。以常規(guī)單變量系統(tǒng)對(duì)改進(jìn)型趨近率進(jìn)行驗(yàn)證,狀態(tài)方程為

取滑模面S=ZX0,可得控制函數(shù)：

通過觀察2種趨近律的相軌跡仿真結(jié)果可以看出,改進(jìn)型趨近率在單變量系統(tǒng)中能收斂到平衡點(diǎn),并且能比傳統(tǒng)指數(shù)趨近律以更快的速度趨近到滑模面。

sgn(S)S-KS2-(f-z2)S

(16)

2.3 基于GWO算法的改進(jìn)滑模自抗擾控制

上述方法不僅解決了傳統(tǒng)擴(kuò)張狀態(tài)觀測(cè)器中的峰值問題,也有效地克制了滑模控制結(jié)構(gòu)中的抖振問題。但是在滑模自抗擾控制方案中,滑模控制部分可變參數(shù)較多,這些參數(shù)需要按照經(jīng)驗(yàn)給定,因此就需要較長(zhǎng)的時(shí)間才能調(diào)整出合適的參數(shù)[22],為了提高參數(shù)的精度,同時(shí)提高效率,本文采用GWO算法對(duì)需要整定的參數(shù)進(jìn)行尋優(yōu)。

GWO算法是一種新興的啟發(fā)式優(yōu)化算法,其基本思想是模擬灰狼群體的社會(huì)行為[23],實(shí)現(xiàn)全局優(yōu)化。

對(duì)灰狼行為建立數(shù)學(xué)模型[24]：

式中：Xp(t)為目標(biāo)狀態(tài);X(t)為灰狼坐標(biāo);D為灰狼與目標(biāo)之間的長(zhǎng)度;X(t+1)為灰狼根據(jù)目標(biāo)狀態(tài)進(jìn)行下一次圍堵的目標(biāo)位置;A和C為控制系數(shù)A=2a·r1-a,C=2r2,其中,r1和r2為大于0小于1的變量,a為非線性收斂因子。

為提高算法的優(yōu)化性能,并避免尋優(yōu)期間陷入局部最優(yōu),本文采用的非線性收斂因子a可表示為

式中：e為自然指數(shù);t為迭代次數(shù);tmax為最大迭代次數(shù)。

適應(yīng)度函數(shù)可表示為

式中：n為采樣總數(shù)。當(dāng)灰狼搜索到獵物位置后,頭狼會(huì)帶領(lǐng)次頭狼和執(zhí)行狼指導(dǎo)其他狼群進(jìn)行捕獵,利用頭狼最靠近獵物的優(yōu)勢(shì),來通過這頭狼判斷獵物位置,從而逐漸逼近獵物,確定灰狼個(gè)體的移動(dòng)方向,不斷更新位置信息,最終確定獵物定位,完成捕獵過程。GWO算法優(yōu)化控制系統(tǒng)步驟如下：

1) 初始化,令時(shí)間為0,迭代次數(shù)t=0,最大迭代次數(shù)tmax,種群數(shù)N;

2) 運(yùn)行程序得到改進(jìn)自抗擾控制參數(shù),計(jì)算出永磁同步電機(jī)模型;

3) 計(jì)算適應(yīng)度函數(shù),運(yùn)行系統(tǒng)模型,記錄當(dāng)前最優(yōu)解;

4) 篩選最優(yōu)參數(shù),循環(huán)次數(shù)N=N+1;

5) 迭代次數(shù)達(dá)到tmax停止迭代,輸出最優(yōu)解。

3 實(shí)驗(yàn)結(jié)果分析及討論

3.1 實(shí)驗(yàn)平臺(tái)搭建

利用Simulink搭建永磁同步電機(jī)控制系統(tǒng),設(shè)定電機(jī)初始參數(shù)如下：

直流母線電壓311 V,電機(jī)轉(zhuǎn)速18 000 r/min,額定電流40.4 A,轉(zhuǎn)子磁鏈0.186 6 Wb,極對(duì)數(shù)4對(duì),交流電感0.964 4 mH,直流電感0.756 6 mH。

3.2 實(shí)驗(yàn)分析

電機(jī)在卷繞細(xì)紗的過程中,隨著管紗上紗線從小紗到大紗的轉(zhuǎn)變,對(duì)應(yīng)的卷繞速度也要做出相應(yīng)的改變。電機(jī)在設(shè)定轉(zhuǎn)速為18 000 r/min,帶負(fù)載TL為50 mN·m時(shí)分別使用了常規(guī)自抗擾算法、滑模自抗擾算法、GWO算法改進(jìn)的滑模自抗擾算法控制電機(jī)模擬細(xì)紗卷繞。首先時(shí)間為600 ms時(shí),改變轉(zhuǎn)速到18 300 r/min,其次時(shí)間為800 ms時(shí),改變轉(zhuǎn)速到18 600 r/min,模擬紗線在卷繞過程中所需對(duì)應(yīng)變動(dòng)的卷繞速度。通過Simulink進(jìn)行仿真驗(yàn)證,得到永磁同步電機(jī)在3種不同算法控制下的轉(zhuǎn)速、轉(zhuǎn)矩波動(dòng)曲線,并對(duì)結(jié)果進(jìn)行對(duì)比分析。圖4為3種不同算法控制下的電機(jī)轉(zhuǎn)速波動(dòng)曲線。

圖4 電機(jī)轉(zhuǎn)速波動(dòng)曲線Fig.4 Motor speed fluctuation curve

從圖4可以看出,3種控制方法都能使永磁同步電機(jī)達(dá)到穩(wěn)定運(yùn)行的狀態(tài),但是各種方法控制下的控制精度、調(diào)速時(shí)間、電機(jī)運(yùn)行的穩(wěn)定性,以及系統(tǒng)的抗干擾能力都有差異。

在常規(guī)自抗擾算法控制下,轉(zhuǎn)速出現(xiàn)了明顯的超調(diào),第1次超調(diào)過后轉(zhuǎn)速穩(wěn)定在18 195 r/min左右,第2次穩(wěn)定在18 484 r/min左右。

在滑模自抗擾算法控制下,采用擴(kuò)張狀態(tài)觀測(cè)器補(bǔ)償了系統(tǒng)的不確定擾動(dòng),用改進(jìn)滑模控制代替了狀態(tài)誤差反饋控制環(huán)節(jié),因此,永磁同步電機(jī)在2次調(diào)速后的轉(zhuǎn)速曲線幾乎都沒有超調(diào),調(diào)速后轉(zhuǎn)速穩(wěn)定值由18 195、18 484 r/min,提高到了18 280、18 570 r/min,更加接近實(shí)驗(yàn)的設(shè)定值,在自抗擾控制的基礎(chǔ)上提高了系統(tǒng)的控制精度。但是系統(tǒng)的抗干擾能力和調(diào)速性能有待提高。

而在GWO算法改進(jìn)的滑模自抗擾算法控制下,超調(diào)最小。改進(jìn)型趨近律滑模控制收斂速度快,且改進(jìn)了非線性收斂因子的GWO算法尋優(yōu)能力更強(qiáng),因此電機(jī)調(diào)速后轉(zhuǎn)速波動(dòng)時(shí)間變短,由180 ms減小到40 ms,達(dá)到穩(wěn)定運(yùn)行的速度更快,并且轉(zhuǎn)速分別穩(wěn)定在18 295 r/min和18 590 r/min,更接近實(shí)驗(yàn)設(shè)定的期望轉(zhuǎn)速。GWO算法改進(jìn)的滑模自抗擾算法能有效提高系統(tǒng)的響應(yīng)速度和控制精度。轉(zhuǎn)速波動(dòng)的減小就盡可能地避免了短暫卷繞速度不匹配、成紗捻度不一致、成紗質(zhì)量較差等問題。

在同等實(shí)驗(yàn)條件下,分別用3種控制方法模擬紗線卷繞過程,測(cè)得電機(jī)調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)曲線。圖5為永磁同步電機(jī)在常規(guī)自抗擾算法控制下電機(jī)轉(zhuǎn)矩波動(dòng)曲線。

圖5 自抗擾算法控制的電機(jī)轉(zhuǎn)矩波動(dòng)曲線Fig.5 Motor torque fluctuation curve controlled by active disturbance rejection algorithm

從圖5可以看出,永磁同步電機(jī)在常規(guī)自抗擾算法控制下,第1次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值達(dá)到了157 mN·m,第2次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值達(dá)到了153 mN·m,瞬時(shí)平均轉(zhuǎn)矩增量為105 mN·m;

圖6為永磁同步電機(jī)在滑模自抗擾算法控制下電機(jī)轉(zhuǎn)矩波動(dòng)曲線。

圖6 滑模自抗擾算法控制下的電機(jī)轉(zhuǎn)矩波動(dòng)曲線Fig.6 Motor torque fluctuation curve controlled by sliding mode active disturbance rejection algorithm

從圖6可以看出,在滑模自抗擾算法控制下,第1次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值減小到了141 mN·m,第2次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值減小到了139 mN·m,瞬時(shí)平均轉(zhuǎn)矩增量減小到90 mN·m。通過比較調(diào)速時(shí)的電機(jī)轉(zhuǎn)矩脈動(dòng)增量可知,引入了滑模控制的自抗擾算法在調(diào)速時(shí),對(duì)永磁同步電機(jī)轉(zhuǎn)矩脈動(dòng)有抑制作用,瞬時(shí)轉(zhuǎn)矩增量減小了14.28%。在滑模自抗擾算法控制下,利用滑模控制魯棒性高的特點(diǎn),能有效提升系統(tǒng)的抗干擾能力。

圖7為永磁同步電機(jī)在GWO算法改進(jìn)的滑模自抗擾算法控制下電機(jī)轉(zhuǎn)矩波動(dòng)曲線。

圖7 改進(jìn)GWO算法的滑模自抗擾算法控制下的電機(jī)轉(zhuǎn)矩波動(dòng)曲線Fig.7 Motor torque fluctuation curve underthe control of sliding mode active disturbance rejection algorithm under improved GWO algorithm

從圖7可以看出,GWO算法改進(jìn)的滑模自抗擾控制算法控制下,第1次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值僅有118 mN·m,第2次調(diào)速時(shí)轉(zhuǎn)矩波動(dòng)峰值僅有122 mN·m,瞬時(shí)平均轉(zhuǎn)矩增量為70 mN·m。

在GWO改進(jìn)的滑模自抗擾算法控制下,利用滑模控制魯棒性高的特點(diǎn),提升了系統(tǒng)的抗干擾能力,利用GWO算法對(duì)滑模控制的參數(shù)進(jìn)行尋優(yōu),保證了參數(shù)的精確性,解決了滑模控制參數(shù)由于設(shè)定不精確,導(dǎo)致系統(tǒng)響應(yīng)速度不高且抖振明顯的問題,因此電機(jī)調(diào)速時(shí)的瞬時(shí)平均轉(zhuǎn)矩增量由105 mN·m減小到70 mN·m,減小了約33.33%,且在調(diào)速時(shí)電機(jī)的轉(zhuǎn)速波動(dòng)減小,系統(tǒng)的調(diào)速性能提高。該控制方法相較于滑模自抗擾控制,能有效增強(qiáng)系統(tǒng)的魯棒性。

通過對(duì)比3種不同算法控制下的電機(jī)轉(zhuǎn)矩波動(dòng)曲線可以看出,電機(jī)在常規(guī)自抗擾算法控制下瞬時(shí)轉(zhuǎn)矩增量最大,滑模自抗擾算法控制下次之,而GWO算法的滑模自抗擾控制算法控制下轉(zhuǎn)瞬時(shí)矩增量最小,且隨后伴隨的轉(zhuǎn)矩脈動(dòng)最小,電機(jī)在整個(gè)運(yùn)行過程中最平穩(wěn)。

實(shí)驗(yàn)證明,改進(jìn)GWO算法優(yōu)化下的基于增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器與改進(jìn)型趨近率滑模控制聯(lián)合改進(jìn)的自抗擾控制策略可有效抑制系統(tǒng)的轉(zhuǎn)矩脈動(dòng),提高成紗質(zhì)量,減少紗線斷頭。

4 結(jié) 語(yǔ)

本文針對(duì)永磁同步電機(jī)驅(qū)動(dòng)細(xì)紗機(jī)卷繞系統(tǒng)調(diào)速后的轉(zhuǎn)速、轉(zhuǎn)矩波動(dòng),導(dǎo)致管紗質(zhì)量不高或紗線斷頭問題,提出了改進(jìn)GWO算法優(yōu)化下的基于增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器與改進(jìn)型趨近率滑模控制聯(lián)合改進(jìn)的自抗擾控制策略。通過搭建永磁同步電機(jī)仿真模型,驗(yàn)證了所提出的控制策略可以降低永磁同步電機(jī)轉(zhuǎn)速、轉(zhuǎn)矩的波動(dòng)。實(shí)驗(yàn)表明,改進(jìn)GWO算法優(yōu)化下的基于增益可調(diào)擴(kuò)張狀態(tài)觀測(cè)器與改進(jìn)型趨近率滑模控制聯(lián)合改進(jìn)的自抗擾控制策略對(duì)系統(tǒng)轉(zhuǎn)速、轉(zhuǎn)矩波動(dòng)降低效果顯著,提高了管紗的質(zhì)量,減少了細(xì)紗機(jī)卷繞過程中紗線斷頭的產(chǎn)生。