一種具有執行器故障的非線性離散系統的迭代學習控制

李丁巳,楊 軒

(西安工程大學 理學院,陜西 西安 710048)

0 引 言

迭代學習控制(iterative learning control,ILC)是一種智能控制策略,其主要思想是,針對一種在固定時間區間上可重復運行的系統,利用以前的學習信息,逐次更新控制信號,使得在此控制信號支配下,逐步實現系統對目標軌線的精確跟蹤[1-5]。與傳統的控制方案相比,ILC的優勢在于它是基于數據的控制策略,無需知道系統的動力學信息,且便于實現,易于維護[4-5]。因此,其經常應用于模型未知,且對精度要求較高的復雜的工業跟蹤控制中。近年來,在基礎理論研究及工程實踐應用方面,ILC都備受關注。但由于工業控制系統通常在不確定的條件下運行,致使ILC系統會在復雜的環境中出現故障,從而導致控制系統的穩定性和跟蹤性能嚴重下降。此外,ILC的可重復性質,導致其對系統中出現的故障尤為敏感。因此,在設計ILC策略的過程中,容錯機制是一個不得不考慮的重要問題。

迭代學習容錯控制(ILFTC)是一種新型控制策略。它是針對因器件磨損、卡頓等不確定情況導致系統故障時而不得不考慮的一種控制技術。目前, 對ILFTC控制策略的研究主要集中在批處理工藝方面,如化工、醫藥生產、現代農業領域等,這主要得益于成熟的二維模型技術。文獻[6-9]討論了這種策略的收斂條件。文獻[10-11]針對故障,提出了可靠的迭代學習控制方案。同樣,文獻[12]利用線性矩陣不等式方法,提出了一種綜合迭代學習控制器。在網絡化背景下,考慮事件觸發傳輸策略和數據丟失的情況,文獻[13]設計了一種滿足魯棒性要求的狀態反饋控制器。此外,基于其他技術的ILFTC研究也取得了一定的成果。如為了便于分析故障造成的影響,文獻[14]將問題從時域轉化為頻域,并提出有效的容錯策略。文獻[15-16]借助模糊理論,提出了基于T-S模糊模型的ILFTC機制。

回顧上述成果不難發現,大多數結論都是在確定故障的情況下得出的。然而,由于實際控制系統經常在不確定的條件下運行,故障的發生具有隨機性,難以提前預測。這就導致具有確定性故障的可靠控制器過于保守,以致限制了其實際應用。實際上,在不同周期和不同時間發生故障的事件是相互獨立的。主要的挑戰是如何制定適當的策略來檢測故障,以分析它們對系統瞬態行為的影響。因此,如何根據故障的發生概率設計ILC算法就成為重要的考慮因素之一。 雖然這一課題近年來已有研究[17-18],但仍有一些不足之處有待進一步完善。如被故障影響的控制系統的統計學行為常常被忽視。因此,從統計的角度進一步研究ILC策略的容錯能力是一項具有現實意義的工作。這促使筆者在這方面做出突破。

本文主要針對執行器故障的隨機性,提出了一種概率意義上的ILFTC算法,當執行器發生隨機故障時,首次從統計意義上分析了被控系統的跟蹤性能,借助λ范數提出了一個控制策收斂的充分條件,以保證所得結果的實用性。

1 問題描述

考慮如下仿射非線性系統：

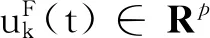
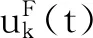
E{αk(t)}=1×P{αk(t)=1}+

需要說明的是,引入隨機變量αk(t)的目的是表述執行器錯誤是否發生。具體地, 如果αk(t)=1,則執行器發生故障;否則,αk(x)=0,則表示執行器不發生故障。 這里0～1 伯努利變量對于任意m≠n,l,s∈Ω,αm(l)與αn(s)相互獨立。

因此, 當收到式(2)所示的控制信號時, 受控系統(1)可表示為

令yd(t)(t∈Ω)表示目標軌線, 并定義跟蹤誤差ek(t)?yd(t)-yk(t), 在迭代學習控制器內, 控制信號按如下的策略進行更新：

uk+1(t)=uk(t)+Γek(t+1)

(4)

式中：Γ是學習增益矩陣。

注1 本文中執行器故障的機理與文獻[17]和[18]不同。在文獻[17]和[18]中,執行器故障獨立發生在每個學習周期的不同時刻,而不涉及不同學習周期的同一時刻的故障模式。由于ILC的工作模式是可重復性,執行器可能會在每個學習周期中任意時刻隨機發生故障。因此,有必要探究在不同的學習周期中同一時刻發生的故障對系統的影響。另外,本文將故障信號分解為乘性故障和加性故障,便于探究故障信號的影響機理,進而分析故障對學習性態的影響,有利于采取必要措施降低故障信號的影響。

為便于理論分析,首先介紹幾個基本假設和引理。

假設1 任意給定yd(t)(t∈Ω)存在唯一的控制信號序列ud(t)和一個適當初始狀態xd(0)使得動態系統

成立。

假設2 非線性連續函數f(·,·)對任意t∈Ω,滿足廣義李普希茲條件, 即?x1,x2∈Rm, 不等式‖f(t,x1)-f(t,x2)‖≤κf‖x1-x2‖成立,其中,κf>0是一個李普希茲常數。

假設3E{xk(0)}=xd(0),?k∈Z+。

注2 假設1是迭代學習控制問題解的存在性問題。假設2的提出是為了方便后續理論分析。事實上,由于f(·,·)：Rm×p→Rm是一個關于xk(t)的連續可微函數,可以利用f(·,·)：Rm×p→Rm的導數信息確定李普希茲常數κf。在工程實踐中,只需知道κf的存在性,而不需要知道其具體值。因此該假設是合理的。假設3是狀態可重置條件,它是ILC的基本問題之一[19-21]。 若該條件不能滿足,通過ILC策略就無法達到對目標軌線精確跟蹤的目的。經典的ILC常常將每次迭代的初始狀態設置為xk(0)=xd(0),以達到精確跟蹤的目的。然而,該假設與之不同。由于隨機發生的執行器故障會降低被控系統的跟蹤精度,導致即使每次迭代的初始狀態設置為xk(0)=xd(0),也很難達到完全跟蹤的目的。于是,在跟蹤能達到所需精度要求的前提下,為便于理論分析,退而求其次,將初始狀態放寬為假設3。

2 主要結果

定理1 設具有故障的控制信號(2)和控制律(4)應用到滿足假設1～3的受控系統(1)。如果學習增益矩陣Γ和故障增益矩陣Ψ(t)滿足

則隨著迭代次數的增加,系統的輸出在Ω上一致跟蹤目標軌線yd(t)到其某個鄰域內。

證明首先, 引入無故障控制信號誤差,有故障控制信號誤差和狀態誤差

由式(6)中第一個方程,并結合式(2)、(4)易知,δuk+1(t)滿足如下遞歸關系：

δuk+1(t)=(I-ΓCBφk(t))δuk(t)-

ΓC(f(xd(t))-f(xk(t)))-

對式(7)兩端取范數,并利用假設2,得

‖δuk+1(t)‖≤‖I-ΓCBφk(t)‖‖δuk(t)‖+

這里,

對式(8)兩邊取期望, 得

E{‖δuk+1(t)‖}≤E{‖I-ΓCBφk(t)‖}

式(9)成立的依據是,隨機變量數學期望的保序性[23]。

另一方面,考慮式(6)中的δxk(t),可得

δxk(t)=f(t,xd(t-1))-f(t,xk(t-1))+

Bφk(t-1)δuk(t-1)+

對式(10)兩側取范數,并考慮假設1,得

‖δxk(t)‖≤κf‖δxk(t-1)‖+b‖φk(t-1)‖

對式(11)兩側取數學期望, 可得如下的不等式

E{‖δxk(t)‖}≤κfE{‖δxk(t-1)‖}+

進一步地, 利用遞歸關系,得

bκfE{‖φk(t-2)‖}E{‖δuk(t-2)‖}+

bE{‖φk(t-1)‖}E{‖δuk(t-1)‖}+

E{‖φk(j)‖}E{‖δuk(j)‖}+

根據假設條件3, 式(13)右側第一項消失. 因此,有

E{‖φk(j)‖}E{‖δuk(j)‖}+

設φk(t)=diag[φ1,k(t),φ2,k(t),…,φp,k(t)], 其中

φj,k(t)=αk(t)σj(t)+(1-αk(t))=

j=1,2,…,p,于是E{‖φk(t)‖}≤?=max{1,σ1,σ2,…,σp}。從而式(14)可變為

將式(15)代入式(9),得

E{‖δuk+1(t)‖}≤E{‖I-ΓCBφk(t)‖}·

E{‖δuk(j)‖}+φ

(16)

這里,a?max{1,kf},λ>1是一個充分大的實數。

將式(18)代入式(17),得

(E{‖I-ΓCBφk(t)‖}+

由于對于任意j∈{1,2,…,p},有

‖I-ΓCBφk(t)‖值也具有如下2種不同的情形。

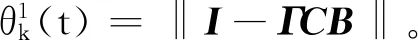
于是,

聯立式(19)和(20),得

根據假設條件(5),易知0<ρ<1顯然成立。另外, 由于a>>max{1,κf}, 則根據實數的稠密性,必存在一個充分大的數λ,使得

成立。因此,根據式(21)和引理1,有

進而

注3 本文的一個創新點是將執行器故障分解成乘性故障和加性故障。這樣處理的好處是可以為尋找消除或減弱故障的方法提供方便。另外,證明過程中, 利用λ范數分析系統的跟蹤性能,并導出算法在數學期望意義下收斂的充分條件。實際上,引入a-λt僅僅改變算法的收斂速度,而決定不了算法固有的收斂性態[24]。因此這種分析方法是可行的。

3 數值仿真

考慮如下的非線性系統：

其中,離散的時間區間為Ω={0,1,2,…,20}。

設目標軌線為

假設初始狀態滿足E{x1,k(0)}=E{x2,k(0)}=x1,d(0)=x2,d(0)=0,初始控制信號為u1,0(t)=u2,0(t)=0, ?t∈Ω。設學習增益矩陣為

易求,‖I-ΓCB‖=0.772 9。

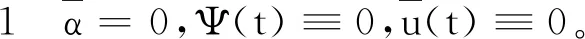
這種情況旨在說明,在沒有任何故障的情況下,對任意給定的一個可達的目標軌線,總可以找到一個最優控制信號,使得在其控制下,系統精確跟蹤的目標可以實現。圖1為跟蹤誤差曲線,圖2為跟蹤性能,其中實線為期望軌跡,虛線為系統經過50次迭代后系統輸出曲線。

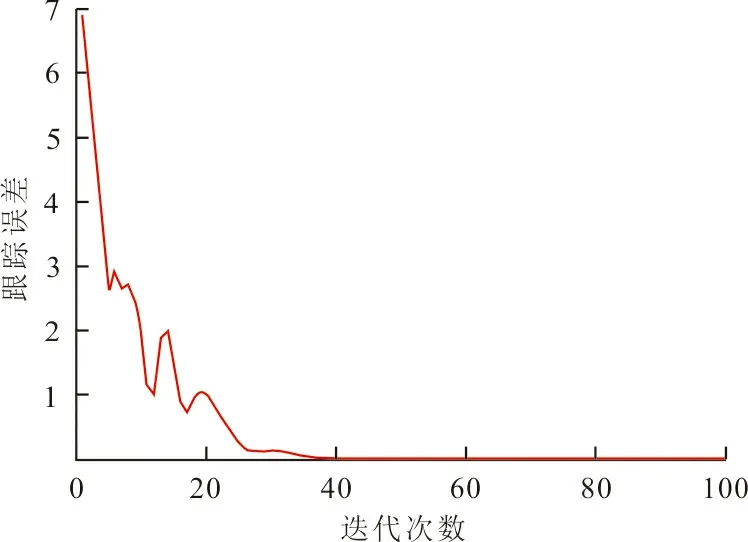
圖1 無故障時‖ek(t)‖2曲線 Fig.1 Curve of ‖ek(t)‖2 when fault is absent

(a) y1,k(t)

從圖1和圖2可以看出,在學習律式(4)的控制下,跟蹤誤差隨著迭代次數的增加在2范數意義下收斂到零,系統(25)的輸出可以精確跟蹤期望軌跡。這說明在不存在故障的情況下,系統能夠準確地跟蹤到所期望的軌跡。

Ψ(t)=diag(0.8+0.1sin(ξ(t)t),0.8+

0.1cos(ξ(t)t))

(26)

式中：ξ(t)是一個在(0,1)內變化的隨機變量。在這種情況下,‖I-ΓCBΨ(t)‖的取值范圍如圖3所示。

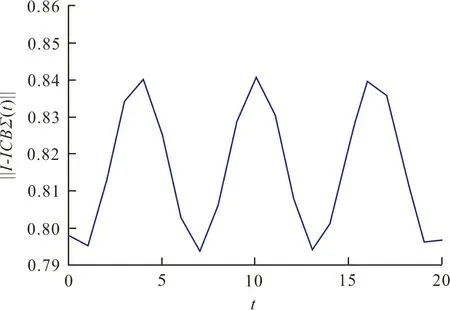
圖3 ‖I-ΓCBΨ(t)‖的取值范圍Fig.3 Rang of ‖I-ΓCBΨ(t)‖

顯然,0.790 0<‖I-ΓCBΨ(t)‖<0.850 0。結合‖I-ΓCB‖=0.772 9,定理1中條件(5)顯然成立。

為了驗證跟蹤誤差在數學期望意義下的收斂性態,實驗重復了100次,用均值近似表示數學期望。仿真結果如圖4、5所示。圖4是誤差均值曲線,均值誤差按計算。其中k是迭代次數,100代表實驗次數。

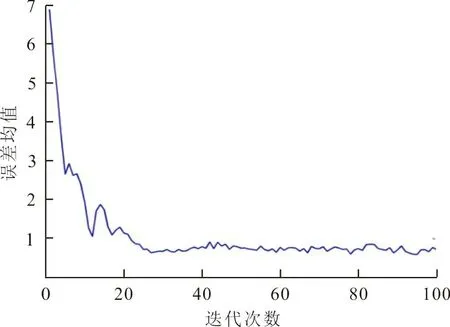
圖4 有故障情況下E{‖ek(t)‖2}曲線Fig.4 Curve of E{‖ek(t)‖2} when fault is present

圖5是在故障發生概率為5%的情況下,最后一個學習過程中,第50次迭代后系統的跟蹤性能曲線。其中,實線是目標軌線,虛線是系統在控制律(2)和(4)控制下的輸出軌線。

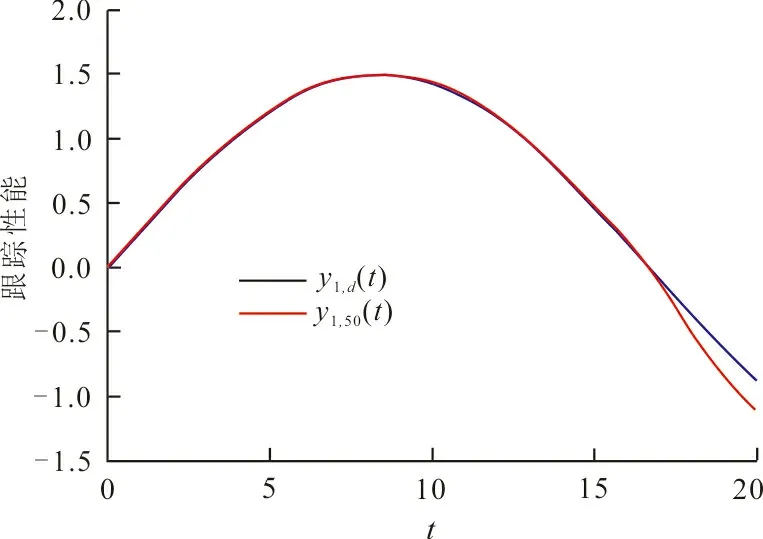
(a) y1,k(t)

由圖4可以看出,在學習律(2)和(4)控制下,E{‖ek(t)‖2}最終會收斂到1以下。由圖5可以看出,第50次迭代后,系統輸出軌線已很接近目標軌線。這表明,雖然發生了故障,但系統輸出隨著迭代次數的增加,仍能一致跟蹤目標軌線到某個鄰域內。

4 結 語

本文針對一類執行器隨機發生故障的離散仿射非線性系統,當故障滿足伯努利分布時,從概率意義上提出了一種迭代學習容錯控制策略。該策略的關鍵是,將執行器故障信號分解為乘性故障信號和加性故障信號。在此基礎上,借助λ范數和范數不等式理論,分析了控制策略的學習性態和故障信號對學習性能的影響機理,并導出了控制策略在數學期望意義下收斂的一個充分條件。為了驗證所得結果的正確性和有效性,將所提控制策略應用到一個具體非線性系統的跟蹤控制中。理論分析和數值仿真結果均表明,當執行器故障以一定的概率發生時,所提策略能夠較好地保持系統的跟蹤精度。后續研究將在本文基礎上,將結論拓展到非仿射非線性系統,并進一步探究故障信號的補償策略,設計更加有效的控制器。