批量歸一化的自適應聯邦學習算法

康宇洋，劉為凱

武漢工程大學光電信息與能源工程學院、數理學院，湖北 武漢 430205

聯邦學習是一種分布式的機器學習框架，其中多個客戶端（例如移動設備）在中央服務器（例如服務提供商）的協調下協作訓練模型（例如基于用戶的歷史文本數據學習下一個單詞的預測器［1］），同時保持訓練數據分散［2］。它實現了數據不動模型動的方法，可以減輕傳統集中式機器學習帶來的許多系統隱私風險和成本。這一領域最近從研究和應用的角度受到了極大的關注，眾多的公司［3］也已經在實踐中部署了聯邦學習。聯邦學習一詞最初由Mcmahan 等［4］于2016 年提出，同時也提出了最為經典的聯邦平均算法（federated averaging algorithm，FedAvg），該算法的流程如下：客戶端在本地訓練數據，多次迭代后上傳更新的模型到服務器。中央服務器聚合所有客戶端的模型并更新全局模型，最后將全局模型傳輸給所有客戶端。這一過程會重復進行若干次，直到達到一定的精度或迭代次數為止。在客戶端與服務端通信時，由于帶寬、能量和功率等資源有限，網絡中的通信可能比本地計算慢很多數量級，由于數據非獨立同分布（non-identical-indepen-dentdistribution，Non-IID）導致客戶端漂移，以及在訓練過程中進行模型更新的通信可能會向第三方或中央服務器泄露敏感信息［5］，這些問題都會嚴重影響聯邦學習的穩定性。

針對這些問題，各種高效的聯邦學習算法開始被提出。文獻［6］提出了FedAvg 在處理異構數據時的不足，并對其進行了一定程度的改進。文獻［7］首次提出了FedAvg 中存在客戶端漂移的問題，并使用了隨機控制平均的聯邦學習算法，在很大程度上解決了客戶端漂移的問題。文獻［8］表明FedAvg 在異構數據上的性能仍然是一個活躍的研究領域，文獻［9］通過假設有界梯度來約束這種漂移，文獻［10］提出或者將其視為附加的噪聲來處理，文獻［5，8］則使用假設客戶端最優值接近的方法，文獻［11］建議使用方差減少來處理客戶端的異構問題。針對聚合策略也提出了很多的算法，文獻［12］假設數據的一個子集在所有客戶之間全局共享，文獻［13］提出了一種非獨立同分布數據分區的聚合策略，該策略以分層的方式共享全局模型。文獻［14］證明了在聯邦網絡中加入批量歸一化（batch normalization，BN）可以極大地提高算法的收斂速度，文獻［15］證明在本地客戶端保留BN 參數可以在一定程度上優化對異構數據的處理，但盲目的加入BN 會導致過擬合的問題。文獻［2］是一篇聯邦學習的綜述性文章，而對于聯邦學習未來的研究方向也可以參考該文獻。

上述方法均對于客戶端漂移以及算法的收斂性單方面進行了一定程度的改進，同時處理這兩個問題的文獻較少。文獻［7］中的算法很大程度上解決了客戶端漂移的問題，但每次與中央服務器通信時，不僅要傳輸模型的參數，還要傳輸控制變量，增加了單次通信代價，這消耗了大量的通信資源，而對自適應參數做一些限制，能夠進一步的節省通信開銷。

受到文獻［7，14］的啟發，在保證性能的前提下，針對算法的收斂速度進行研究。在FedAvg 以及文獻［7］的基礎上，提出了利用自適應變量將模型的更新方向由局部最優指向全局最優，同時只利用最后一個梯度來更新自適應變量，這能夠在一定程度上減少通信開銷。而受到文獻［14］啟發，在訓練模型時加入BN 并在上傳服務器時保留BN 層參數在本地，從而在保證收斂速度的前提下節省通信開銷。

1 聯邦學習算法

1.1 聯邦學習拓撲

傳統的聯邦學習星型拓撲如圖1 所示，由1 個服務器以及n個客戶端所組成，在訓練開始前服務器會將模型的初始模型參數x廣播給各個客戶端，所有的客戶端將其下載到本地，然后使用本地的數據進行訓練并更新局部模型參數xi。在更新完成后將其上傳到服務器，服務器將所有的參數進行聚合然后將其進行加權平均并再次廣播給各個客戶端，重復上述步驟若干次。 其中，第i(i= 1,2,…,n)個客戶端上的局部損失函數如圖1所示，其中表示第i個客戶端第k（k=1，2，…，N，N為正整數）次通信時的客戶端模型參數，xk+1表示聚合后的全局模型參數以及第k+1 次通信時的客戶端模型參數。

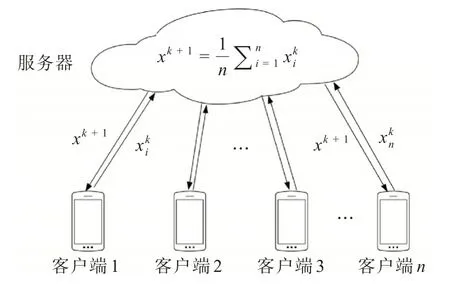
圖1 星型拓撲Fig.1 Star topology

式（1）表示為本地客戶端執行的一次梯度下降：

其中ηl表示客戶端學習率，yi為第i個本地客戶端的模型參數，函數gi表示對第i個客戶端模型求梯度。

式（2）表示對全局模型執行的一次更新，各個客戶端將訓練好的模型參數進行聚合，然后按照抽樣客戶端的比例對全局模型進行更新。

其中S表示被抽取的客戶端數量，ηg為服務端學習率。

1.2 客戶端漂移

客戶端漂移如圖2 所示，x為初始時刻的模型參數，y1和y2為客戶端上的局部模型參數，client1和client2 上的模型在訓練時均朝著局部最優解，前進，而全局最優x?并不等于聚合后的客戶端損失函數最優的平均，兩者之間的差距造成了客戶端漂移的問題。

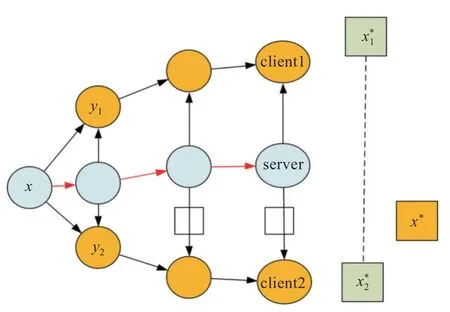
圖2 客戶端漂移示意圖Fig.2 Illustration of client drift

圖3 為文獻［7］在單客戶端上的更新步驟，在本地進行梯度下降時加入自適應變量c對模型進行修正，其中向下的箭頭表示控制變量修正的方向，通過控制變量可以將模型參數x的更新方向從局部最優修正為全局最優x?。

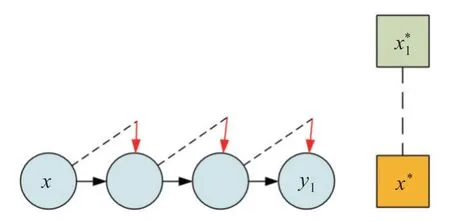
圖3 修正偏移示意圖Fig.3 Illustration of corrected drift

控制變量具體的更新規則在式（3）中給出，其中c為全局修正變量，ci為局部修正變量。

1.3 協變量偏移

協變量偏移［16］是輸入數據分布不一致的一種現象，由于聯邦學習通常處理非獨立同分布數據，從而導致協變量偏移的問題。對數據做去相關性并且突出數據之間的分布相對差異，這對處理異構數據有很大的幫助，BN 可以做到這點。BN 是歸一化的一種手段，這種方式通過減小圖像之間的絕對差異，突出相對差異。在聯邦學習模型中加入BN 層可以加快訓練的速度。

1.4 批量歸一化算法

首先提出凍結的批量歸一化（frozen batch normalization，FrozenBN）算法，由于BN 依賴于均值和方差，如果歸一化批量大小（normalization batch size，NBS）太小，計算的均值和方差并不穩定且無意義。使用FrozenBN 將均值，方差等統計量固定住可以有效緩解BN 本身存在訓練和測試的不一致性［17］，具體操作為判斷當前狀態是否為訓練，若是則將當前狀態改為測試，反之不變，下面的算法為FrozenBN 算法。

輸入：本地迭代次數NE，本地模型x以及控制參數t

1.5 聯邦學習算法

提出批量歸一化的自適應聯邦學習算法（adaptive federated learning algorithm based on batch normalization，FedAB），算法使用了自適應變量處理客戶端漂移的問題，BN 層處理協變量偏移的問題加快算法收斂速度。下面的算法為FedAB 算法。

輸入：服務器初始模型參數x，自適應參數c，全局學習率ηg，客戶端自適應參數ci，局部學習率ηl

對于客戶端漂移的問題，客戶端進行梯度下降更新模型參數時，算法使用自適應變量c對模型參數進行修正，具體操作見1.2 節。為節省算力，在進行梯度下降過程中只使用最后一個梯度對自適應變量進行更新。對于協變量偏移的問題，在客戶端上傳本地模型進行聚合時判斷本地網絡模型的每一層是否為BN 層，如果不是則上傳模型進行聚合，反之則保留該層參數在本地，在節省了通信成本的同時避免了盲目使用BN 層出現的過擬合問題。當NBS 較小時，將BN 替換為FrozenBN，同時加入驗證集以解決該問題。具體方法為每訓練到一定輪次時判斷當前損失值是否大于上一輪，如果小于繼續訓練，反之則會使用上一輪的模型參數繼續進行訓練。

2 仿真結果與結論

本節中評估了所提出算法的性能，設置了多個實驗，使用不同的深度神經網絡從收斂速度以及測試精度對幾種算法進行比較。下面介紹實驗設置和結果。

2.1 實驗設置

為了測試批量歸一化的自適應聯邦學習算法在聯邦學習系統中的性能，使用1 臺臺式電腦作為中央服務器，10 臺筆記本通過無線局域網連接充當客戶端。假設這些客戶端不會對模型發起攻擊，也沒有受到外部病毒的惡意攻擊。

2.1.1 參與比較的算法 為了評估算法的性能，選擇了4 種聯邦學習算法進行比較。

（1）FedAvg：標準的聯邦平均算法。

（2）隨機控制平均算法（stochastic controlled averaging for federated learning，Scaffold）：在FedAvg的基礎上使用了控制變量。

（3）聯邦批量歸一化算法（federated learning on Non-IID features via local batch normalization，FedBN）：使用批量歸一化層的算法，在模型中引入BN 層并保留該層參數在本地。

（4）FedAB：批量歸一化的自適應的算法，在保證精度的前提下提升算法的收斂速度。

2.1.2 模 型 為評估算法的有效性，選擇了2 個深度神經網絡進行仿真實驗。

（1）多層感知機（multi-layer perceptron，MLP）：該模型包含2 個隱層，神經元數量分別為30 個和20 個，無偏置，選擇線性整流函數（linear rectification function，ReLU）作為激活函數。第一層和最后一層的神經元個數分別是784個和10個。

（2）卷積神經網絡（convolutional neural network，CNN）：該模型由2 個卷積層、3 個全聯接層以及2 個殘差塊組成，每個殘差塊中有2 個卷積層。包括殘差塊內的卷積層在內，每個卷積層后都有1 個FrozenBN 層、ReLU 函數以及最大池化層，全連接層的第一層的神經元個數為800 個，最后一層為10 個。

2.1.3 數 據 實驗選擇使用時裝數據集（fashionmixed national institute of standards and technology database，Fashion-MNIST［18］）以及圖像10 分類數據集（Canadian institute for advanced research-10，Cifar-10［19］）做仿真。

（1）Fashion-MNIST：它包含了衣服，鞋，包等10 種日常用品的60 000 個用于訓練和10 000 個用于測試的10 類灰度圖像樣本，其中每幅圖像的維數為28×28 維，在訓練之前將其進行數據增廣，把每張圖片的維數放大成32×32 維并重新進行裁剪，所有數據都是獨立同分布的數據，訓練時將訓練集以4∶1 的比例重新劃分為訓練集和驗證集。

（2）Cifar-10：它包含了動物，交通工具等10 種常見物體的60 000 個彩色RGB 圖像，其中每幅圖像的維數為32×32，50 000 個用于訓練，10 000 個用于測試，數據類型屬于Non-IID，同樣的，在訓練時將訓練集以4∶1 的比例重新劃分為訓練集和驗證集。

2.1.4 其他配置 客戶端總數N設置為10 個，客戶端本地迭代次數（NE）根據與中央服務器的通信輪數（NC）的不同而不同，當NC為3 時，NE設置為30；當NC為20 時，NE設置為3，每次中央服務器與客戶端進行通信時將從10 個客戶端中抽取3 個客戶端進行通信，數據的批處理大小，即一次訓練的樣本數目設置為64 個。

2.2 仿真結果分析

針對客戶端的數據來源，由于每個客戶端的數據都是獨立的，因此應該將下載的數據集平均分配給所有的客戶端。以Cifar-10 數據集為例，每個客戶端可以獲得6 000 個數據，其中5 000 個數據用于訓練，剩余1 000 個數據用作驗證集。在全局模型聚合后，使用10 000 個測試數據測試模型的學習效果。表1 展示了4 種算法在Fashion-MNIST 數據集上的測試精度。

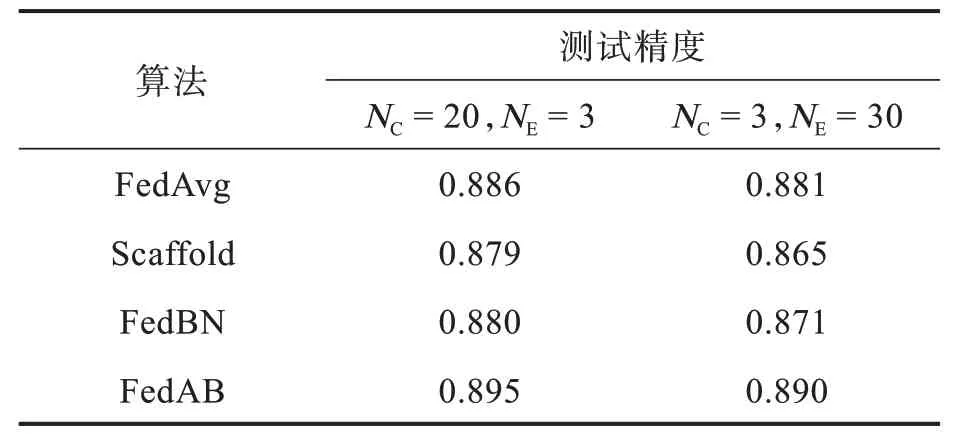
表1 Fashion-MNIST 數據集測試結果Tab.1 Fashion-MNIST dataset test results

圖4（a）是在NC為20，NE為3 時，4 種算法在Fashion-MNIST 數據集上的精度對比圖。由于在FedAB 算法中客戶端與服務器通信時上傳模型會將控制變量c同時進行上傳，而控制變量c是維數與權重相同的矩陣，使得其算法在通信時對比FedAvg 會增加1 倍的通信開銷，從而導致算法收斂速度較慢，但從圖4（a）中可以看出，即使在增加了通信開銷的前提下，FedAB 的表現仍然是4 種算法中最好的，精度比FedAvg 高近一個百分點，而FedBN和Scaffold算法的精度則相差不大。圖4（b）是在NC為3，NE為30 時，4 種算法在Fashion-MNIST 數據集上的精度對比圖，可以看出，FedAB的精度仍然是4 種算法中精度最高的，依然高于FedAvg 近一個百分點精度，FedBN 與Scaffold 算法的精度處于二者之間。從圖4（b）可以看出，在NE大于10 輪時，FedAB 算法的收斂速度大于其余3 種算法，并且在保證收斂速度的同時精度也是4種算法中最高的。

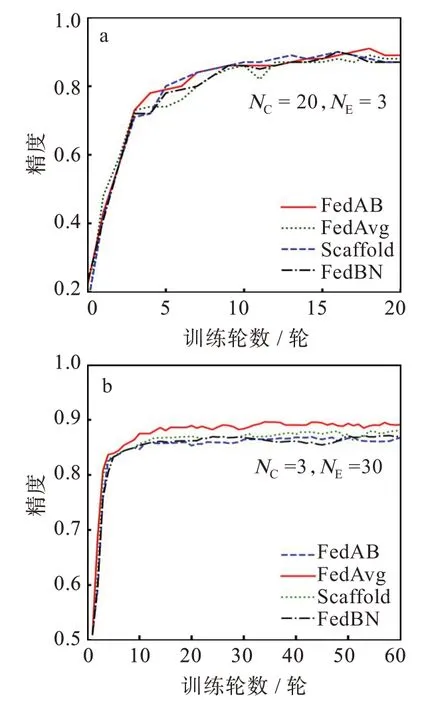
圖4 Fashion-MNIST 數據集各算法精度曲線Fig.4 Accuracy curves of each algorithm in Fashion-MNIST dataset

由于Fashion-MNIST 數據集為簡單的小型數據集且獨立同分布，該數據集無法體現FedAB 的優勢，為了證明該算法的穩定性，進行了在非獨立同分布數據集上的實驗。但是，聯邦學習在非獨立同分布數據集上的應用仍然具有挑戰性［1］。由于數據不獨立且同分布，局部隨機梯度并不能被看作是全局梯度的無偏估計。表2 中呈現了4 種算法在Cifar-10 數據集上的測試結果。

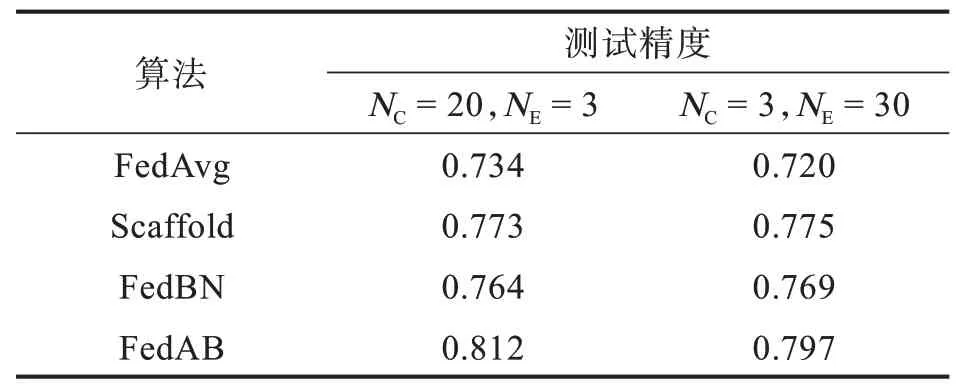
表2 Cifar-10 數據集測試結果Tab.2Cifar-10 dataset test results

與之前的設置一樣，圖5（a）是NC為20，NE為3時4 種算法的精度對比圖，可以看到，FedAB 算法收斂速度遠超其余3 種算法，在Cifar-10 數據集上仍然達到了0.812 的精度，遠高于其余幾種算法，與之相比，FedAvg 暴露出客戶端漂移的問題，NC逐步增加時，本地的模型在訓練的過程中會產生偏移，導致FedAvg 在處理異構數據上顯得有些力不從心，只達到了0.734 的精度。FedAB 精度達到穩定時的訓練輪數為7，而FedAvg 為10，與之相比收斂速度快30%。同樣的，Scaffold 算法與FedBN算法的收斂速度基本一致，精度也相差不大。圖5（b）為與圖5（a）相同的設置參數的情況下4 種算法的損失函數對比圖，可以更加直觀的看到FedAB 的收斂速度遠超其他算法。由于在文獻［7］中已經證明Scaffold 算法的精度以及收斂速度大于FedAvg，所以這里只對比FedAB 與Scaffold 兩種算法的收斂速度以及精度。同樣的，圖6（a）與圖6（b）是NC為3，NE為30 時2 種算法的結果對比，可以看到FedAB 算法的收斂速度雖然與NC為20時相比要慢一些，但其精度與收斂速度仍然是其中最高最快的，FedAB 精度達到穩定時的訓練輪數為10 輪，而Scaffold 為15 輪，與之相比收斂速度快30%。

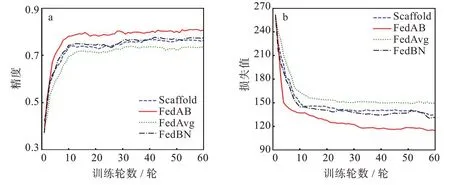
圖5 Cifar-10 數據集各算法對比圖：（a）精度曲線，（b）損失曲線Fig.5 Comparison of algorithms in Cifar-10 dataset：（a）accuracy curves，（b）loss curves

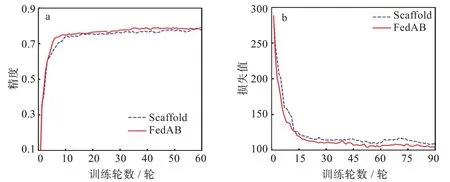
圖6 Cifar-10 數據集Scaffold 與FedAB 算法對比圖：（a）精度曲線，（b）損失曲線Fig.6 Comparison of Scaffold and FedAB algorithms on Cifar-10 dataset：（a）accuracy curves，（b）loss curves

2.3 參與率影響

實驗測試了不同參與率下FedAB 算法對MLP 網絡和Fashion-MNIST 數據集的精度影響［20］。參與率K是指客戶端參與通信的比例，服務器根據參與率隨機選擇一部分客戶端參與通信。圖7 結果顯示，改變參與率對模型的最終穩定性影響不大。但在低參與率情況下，模型收斂速度更快，通信輪數也減少，這能夠節省大量通信資源。考慮到實際環境中客戶端基數龐大，若使用適當的參與率即可獲得合適效果，將能夠極大地減少通信資源。

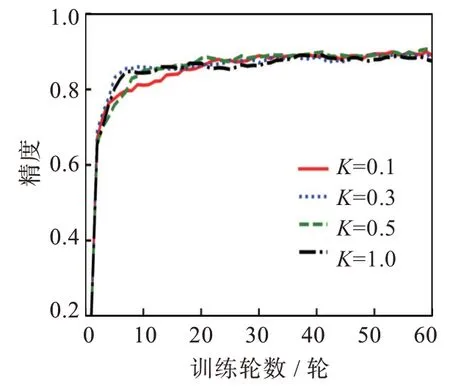
圖7 不同參與率精度曲線Fig.7 Accuracy curves of different participation rates

3 結 論

本文針對聯邦學習算法收斂速度問題，提出了批量歸一化自適應算法。該算法通過自適應參數解決聯邦學習中客戶端漂移的問題，并使用批量歸一化的方法解決協變量偏移的問題，從而提高了算法的精度和收斂速度［21］。實驗結果表明，相比于經典的FedAvg，該算法精度和收斂速度均提高了約30%。在非獨立同分布的數據實驗中，算法在設備低參與率的情況下也能夠達到預期的效果。由于實驗假設客戶端與服務器處于理想狀態下，并未考慮安全問題，在實際應用中，存在客戶端攻擊以及外部惡意病毒攻擊等問題，在未來的工作中需要進一步探索更有效的策略，并且為算法的性能提供更多的理論論證，從而提升算法的泛化能力。