考慮橢圓孔偏轉角組合的凹槽葉頂氣熱性能優化研究

郭嘉杰,梁崇治,郭振東,宋立明,李軍

(1. 西安交通大學能源與動力工程學院,710049,西安;2. 東方汽輪機有限公司電站服務事業部,618000,四川德陽)

渦輪動葉葉頂間隙的存在導致了葉頂泄漏流及泄漏損失的產生,與葉頂相關的損失約占葉柵總氣動損失的1/3[1],葉頂相對間隙的擴大會導致級效率的急劇下降[2-3],同時泄漏流由于葉頂的節流作用往往具有高溫、高速、邊界層薄的特征,故而葉頂設計往往需要兼顧冷卻、氣動兩方面的問題[4]。

泄漏流經過葉頂節流作用形成了復雜的渦系結構,結合流動結構分析對氣動損失研究具有重要意義。Denton[5]對葉柵內氣動損失成因及效應進行了分析,并建立了損失模型。Sjolander等[6]對平葉頂泄漏流結構進行了分析,發現葉頂壓力面角區分離渦的形成與葉頂間隙與葉片厚度有關。Heyes等[7]指出厚葉片最大流線收縮處的靜壓要低于薄葉片,導致相同驅動壓差下厚葉片的泄漏流量更大。Kwak等[8-9]通過平葉片實驗測量發現,葉頂相比于機匣面及葉身上部具有最高的換熱系數,增加葉頂間隙會導致葉頂換熱系數及氣膜冷卻效率增加。

隨著渦輪入口溫度與壓力的不斷升高,凹槽葉頂對于提高葉頂氣熱性能的重要性逐漸得到廣泛認識[10-11],同時由于葉頂具有較高熱負荷,是葉柵內最易發生高溫失效的部位之一[12],建立考慮葉頂射流的模型更符合實際工作情況。Niu等[13]研究認為,葉頂尾緣的射流對氣動及換熱性能的影響更為顯著。Zhou C.等[14]對比了平葉頂、吸力面肩壁、凹槽葉頂結構中多葉頂間隙下射流流量對葉柵氣動性能的影響。Volino[15]通過實驗發現葉頂垂直射流對損失影響較小,而朝向壓力面側傾斜射流能滯后平葉頂泄漏渦的形成并降低通道內的湍流度,有效降低了泄漏損失,但對凹槽葉頂的影響相對較弱。Gao等[16]對平葉頂及凹槽葉頂的射流影響進行了研究,認為葉頂間隙、射流流量、葉頂結構存在交互影響。Zhou Z.等[17]對壓力面上部射流、葉頂射流、機匣射流對凹槽葉頂與凹槽小翼葉頂的換熱、冷卻性能影響進行了研究。于金杏等[18]對凹槽葉頂壓力側射流影響進行了研究。軒笠銘等[19]在機匣相對運動情況下對凹槽葉頂進行了氣動分析,認為葉頂射流雖然降低了凹槽葉頂的氣動效率,但同等射流條件下凹槽葉頂相對于平葉頂降低了20%的泄漏損失。許承天等[20]研究了凹槽葉頂射流的脈動特性對氣熱性能的影響。

確定造型參數后,結合優化算法可以進一步地提升葉片的氣動及冷卻性能。Kang等[21]采用肩壁厚度、前彎半徑、后彎半徑、凹槽深度對凹槽葉頂進行了參數化,結合Kriging方法繪制了不同葉頂間隙下渦輪性能參數隨凹槽深度與肩壁厚度變化的曲線。金家輝等[22]通過Kriging代理模型擬合了葉頂形狀對泄漏流量及總壓損失的影響趨勢,最優葉頂結構有效提升了氣動性能。李琛璽等[23]采用全局優化算法對凹槽葉頂冷卻孔布局進行了優化,有效提升了氣膜冷卻效率,同時通過數據挖掘技術辨明了具有顯著影響的參數。

調整葉頂冷氣孔傾斜角度可以在提高冷卻效率的同時有效降低泄漏流量,目前雖然有較多關于凹槽葉頂射流影響的研究,但仍缺少關于凹槽葉頂冷卻孔偏轉角影響的系統性研究,對于葉頂冷卻孔偏轉角也缺少合適的參數化方法,進而難以開展系統的優化研究。因此,本文提出了一種適用于凹槽葉頂的圓形孔及橢圓孔的組合偏轉角參數化方法,并基于Kriging代理模型開展了優化研究,設計結果有效提高了氣膜冷卻效率并降低了泄漏流量,具有一定的凹槽葉頂氣動與換熱優化設計的參考意義。

1 計算模型與數值方法

1.1 幾何模型

本文數值模擬參考模型為Ahn等[24]的單列動葉葉柵實驗平臺,研究工況為靜止葉柵的穩態流動。圖1展示了葉柵的幾何模型及其參數,葉柵軸向長度為86.1 mm,進氣方向與軸向夾角為32°,垂直進氣截面寬度為77.75 mm。葉片型線為GE-E3燃機第一級動葉葉頂型線等比放大3倍,葉頂冷卻布局采用簡化模型,僅設置冷卻孔,未劃分充氣室。含凹槽葉身高度為127.08 mm,葉頂間隙取葉高的1.5%(1.97 mm),肩壁厚度為2.286 mm,凹槽深度為5.08 mm,圓形冷卻孔直徑為1.27 mm,橢圓孔保持相等截面面積,長短軸比為4∶1,沿中弧線布置7個冷卻孔。

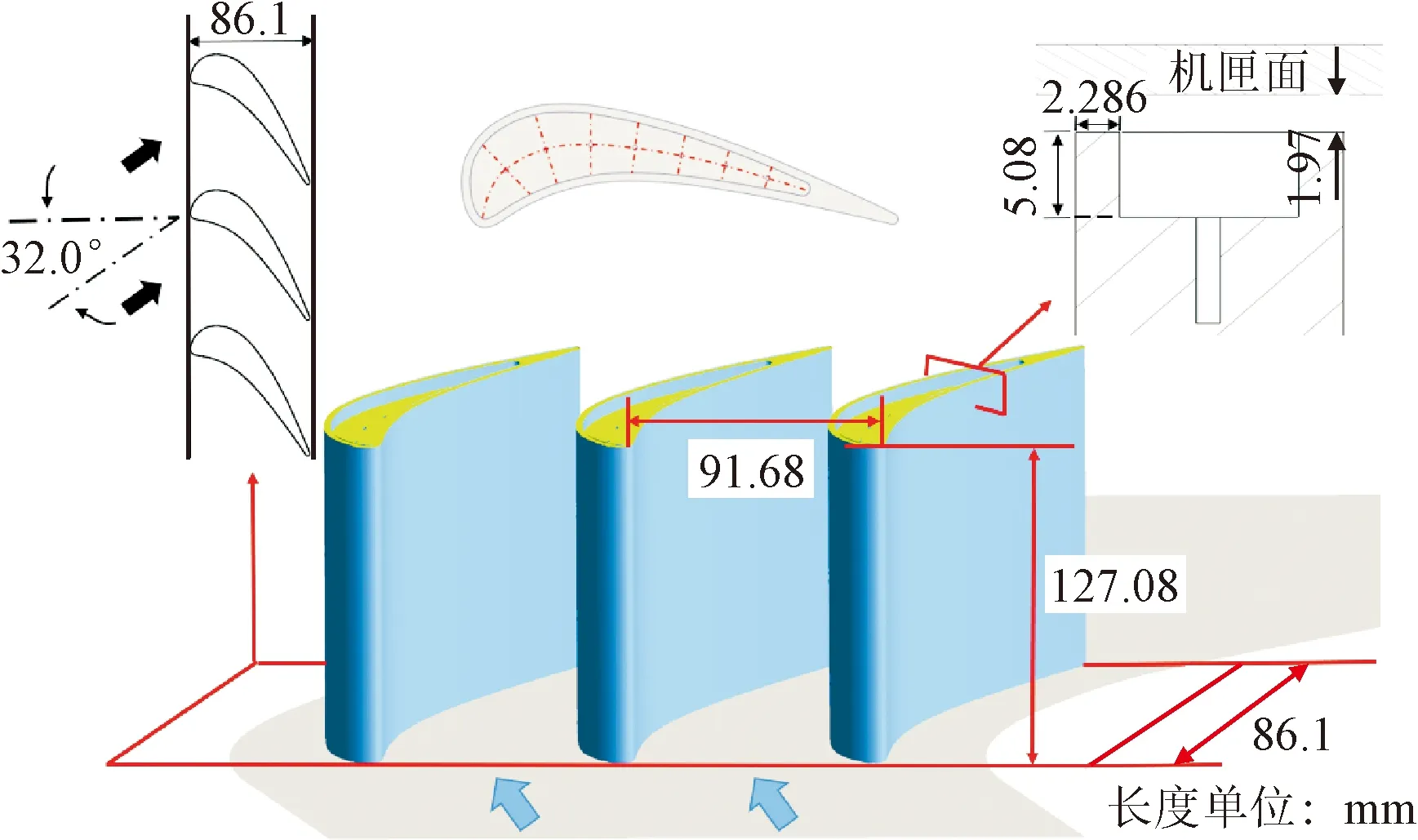
圖1 葉柵與凹槽葉頂幾何模型Fig.1 The geometry of the cascade and the squealer tip

1.2 參數定義

用流向渦量表征當地的旋流強度,定義如下

ωs=[(?w/?y-?v/?z)u+(?u/?z-?w/?x)v+

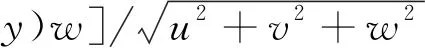
(1)

(2)

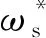
1.3 邊界條件

使用ANSYS ICEM 19.2商業軟件劃分結構化網格,對壁面邊界層網格進行加密,給定壁面第一層網格高度為1 μm,使計算得到的主要關注區域的邊界層第一層網格Y+<1,整體Y+<2,網格模型如圖2所示。

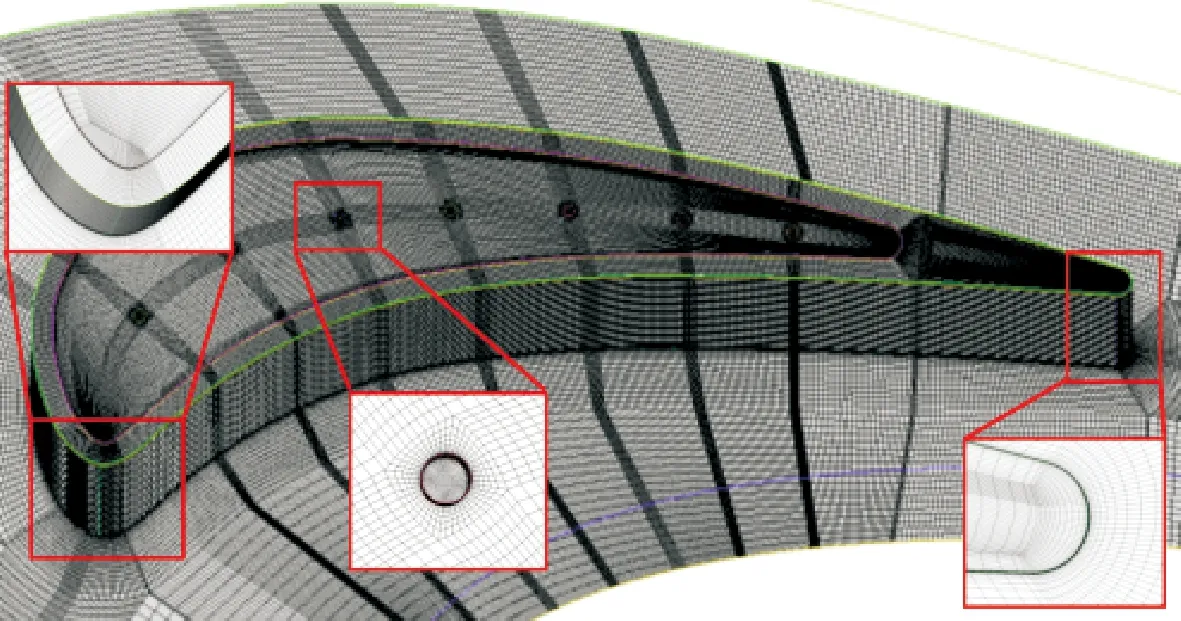
圖2 網格模型Fig.2 Numerical grid

采用ANSYS CFX 19.2商業軟件求解穩態RANS方程組,參考Ahn等[24]的實驗參數設定流道進出口邊界條件,如表1所示。主流湍流度為9.7%,特征長度為0.015 m;給定冷卻射流流量為1.60 8 g/s,折合吹風比為M=1.0,可視作燃機氣膜冷卻的典型工況;流道兩側設置為周期性邊界條件。

表1 邊界條件

1.4 數值驗證

葉頂間隙泄漏流屬于壁面約束流動,采用近壁面湍流模型能更好的模擬流動換熱情況,本文選用標準k-ω、SSTk-ω兩種低雷諾數模型以及標準k-ε高雷諾數模型進行對比。由于具有葉頂氣膜孔的流動換熱實驗數據較少,此處選取了無氣膜冷卻的凹槽葉頂實驗數據[25]進行驗證,如圖3所示。可以發現,在凹槽前緣存在泄漏流再附區,產生了高換熱系數區域,而標準k-ω模型區域分布范圍與實驗數據最為接近。從橫向平均換熱系數對比可以發現,湍流模型對前緣高換熱系數區域普遍存在過預測現象,而標準k-ω模型的換熱系數變化區域與實驗數據最為符合,可以認為標準k-ω模型具備較好地預測凹槽葉頂間隙內流動、換熱特性的能力,本文之后的研究均將采用標準k-ω模型。

(a)實驗數據[25]

(b)標準k-ε

(c)標準k-ω

(d)SST k-ω

(e)橫向平均換熱系數

表2對比了6.41×106、8.72×106、13.46×106這3種網格節點數計算得到的凹槽底部氣膜冷卻效率。可以看出,當網格數增長到8.72×106后,計算誤差率已經小于0.1%,計算結果的網格無關性已達到較高水平,滿足開展凹槽葉頂氣動換熱研究要求,因此此后的研究均將采用該網格數量下的網格節點設置方式。該網格節點設置方式也與湍流模型驗證時使用的網格一致。

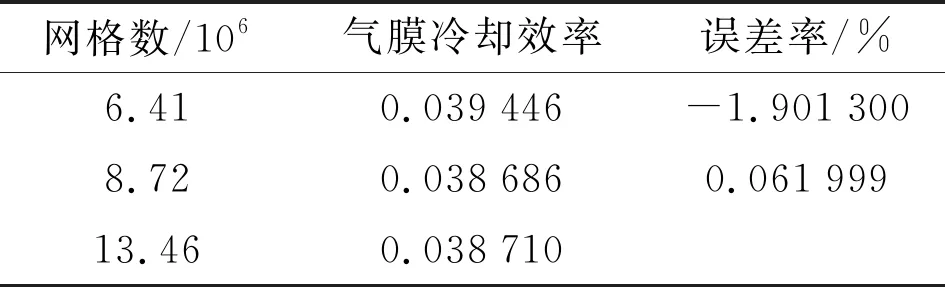
表2 網格無關性驗證

2 優化設計方法

2.1 優化框架與平臺

根據組合偏轉參數化方法,構建凹槽葉頂冷卻孔參數化模型,耦合三維RANS定常流場求解方法、Kriging代理模型優化方法,建立了凹槽葉頂冷卻孔組合偏轉角氣熱優化框架,如圖4所示。該框架可分為:①Kriging代理模型優化模塊,該模塊根據樣本變量與目標函數建立響應面,在響應面內按EI準則進行尋優,將搜尋到的設計變量值返回并輸入幾何模型,通過多次迭代更新響應面以獲取最優解;②幾何建模模塊,該模塊獲取輸入值并替換初始模型的設計參數,通過二次建模的方式構建幾何模型并導入CFD模塊;③數值模擬模塊,該模塊根據導入的幾何模型生成對應的網格模型,在CFD工程中根據預設的邊界條件進行流場求解,提取計算結果的性能參數并構建目標函數,將對應的幾何參數與目標函數輸入Kriging代理模型中進行更新。3個模塊分別依靠pyKriging開源程序包、UG商業軟件、ANSYS ICEM與ANSYS CFX商業軟件實現,通過自主編寫的優化軟件進行調用并實現自動優化。

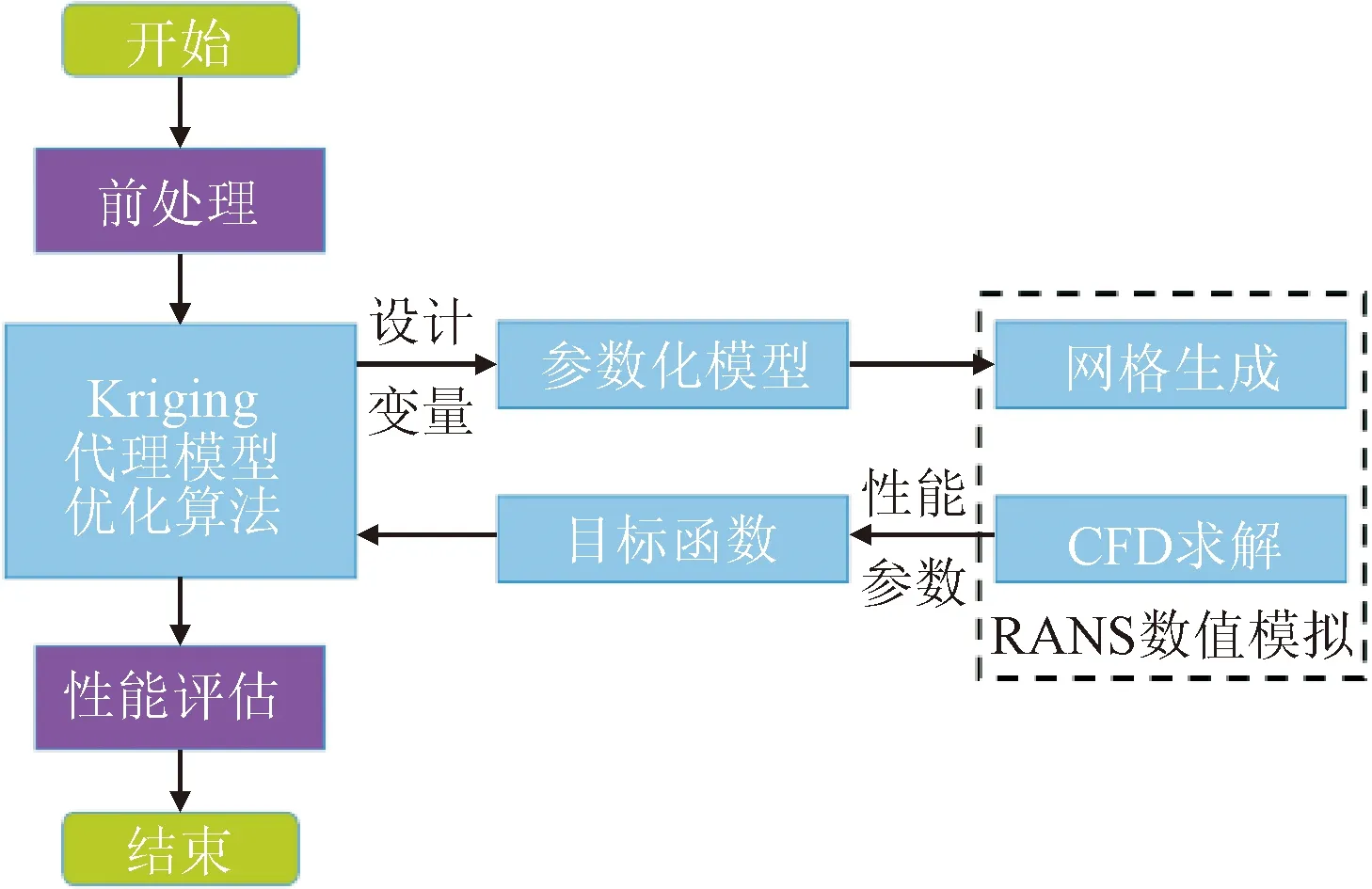
圖4 基于Kriging代理模型的優化框架Fig.4 Optimization procedure based on Kriging surrogate model

2.2 優化算法

本文采用的Kriging代理模型優化算法結合了EI加點準則,也稱為EGO優化算法,該算法的實現流程如下:①采用拉丁超立方采樣方法對設計空間進行采樣;②計算得到全部樣本性能參數及對應的目標函數,使用Kriging方法構建響應面并獲得響應面內的最優值;③根據EI準則計算得到目標函數最優值提升期望最高的空間點,計算該位置的實際目標函數值并更新代理模型,反復迭代直至獲得最優值。

該優化算法能快速、可靠地建立設計變量與性能參數的對應關系,所需建立的樣本量較少,適合本文所進行的凹槽葉頂冷卻孔組合偏轉角的影響研究。

2.3 參數化方法

組合偏轉結構的構建方法如圖5所示,該參數化方法依靠中弧線劃分偏轉方向,對于圓形冷卻孔的組合偏轉參數化共兩個維度,分別為徑向偏轉與軸向偏轉,橢圓孔則增加了自偏轉維度。在中弧線的垂面與切面內分別存在徑向偏轉角(α)與軸向偏轉角(β),根據矢量合成原理做出組合偏轉線(紅色標注),在組合偏轉線的垂面內作出冷卻孔型線,向下切削出成型孔。橢圓孔存在自偏轉角度(γ),該偏轉角存在于組合偏轉線的垂面內。

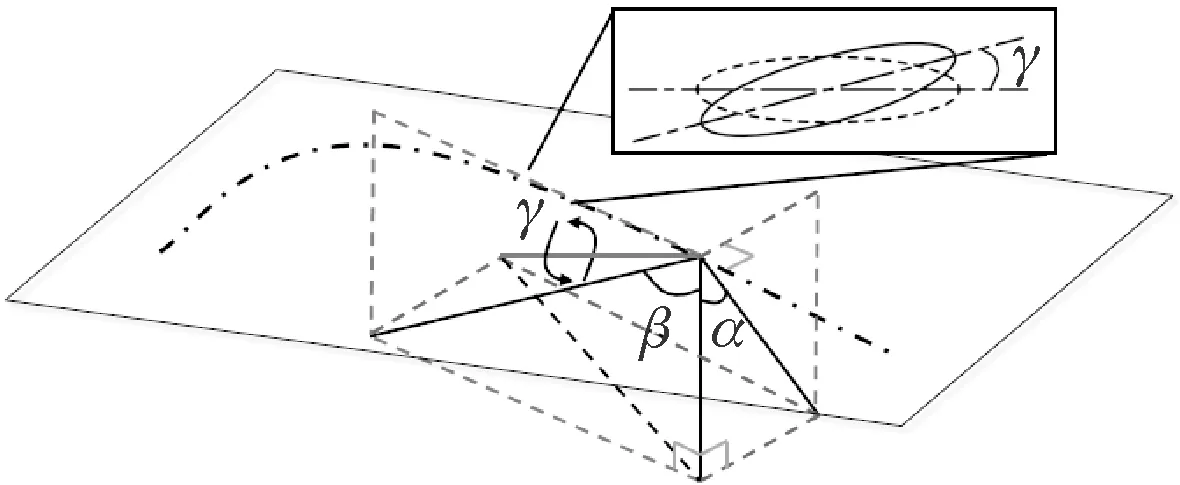
圖5 冷卻孔組合偏轉結構示意Fig.5 Schematic of the combined inclination cooling hole

以徑向偏轉出口朝向壓力面作為正徑向偏轉角,以軸向偏轉出口朝向凹槽尾緣作為正軸向偏轉,橢圓孔初始長軸方向為組合偏轉線垂面與凹槽底面的交線方向,并將逆時針方向作為正自偏轉方向,圖中所標識的偏轉角(α、β、γ)均為正偏轉角。該組合偏轉的參數化方法具有方向特征明確、偏轉角度獨立、參數變化靈活的特點,對于給定的偏轉角度具有唯一對應的幾何結構,即結構的建立不依靠偏轉角的指定順序,適合進行結構優化方面的研究,圖6給出了橢圓冷卻孔組合偏轉的三維構型。

圖6 冷卻孔組合偏轉三維結構Fig.6 Schematic of the combined inclination cooling hole

2.4 優化變量與目標函數

本文分別開展了基于圓形冷卻孔的徑向與軸向組合偏轉優化、基于橢圓孔的自偏轉優化兩個算例的研究。對于圓形冷卻孔而言,設計變量分別為1～7冷卻孔的徑向偏轉角和軸向偏轉角。為減少設計變量的數量以提高優化計算速度,根據冷卻孔所處位置的流動復雜程度,共設置了4組獨立變化的組合角。第1、2冷卻孔由于靠近泄漏流再附區,偏轉角各自獨立變化;第3、4冷卻孔位于過渡區,徑向、軸向偏轉角分別設置為相等;第5～7冷卻孔靠近尾緣區,徑向、軸向偏轉角分別設置為相等。共獲得8個設計變量,如表3所示。

根據圓形冷卻孔優化結果中的組合偏轉角度,將冷卻孔替換為橢圓孔,并開展橢圓孔自偏轉角的優化研究,7個冷卻孔的自偏轉角度獨立變化,共獲得7個設計變量,如表4所示。

表3 圓形孔設計變量及變化范圍

表4 橢圓孔設計變量及變化范圍

本文的優化期望為通過組合偏轉優化的同時提高凹槽葉頂的冷卻性能與氣動性能,故將目標函數設置為葉頂氣膜冷卻效率的變化率與比泄漏流率的變化率的加權和。本文對比泄漏流率與冷卻效率的考量具有相同比重,但由于比泄漏流率的變化率遠小于冷卻效率,故在比泄漏流率變化量前設置了較高系數來保證變化范圍的平衡,目標函數構建為

(3)

3 優化結果討論

為直觀對比圓形孔與橢圓孔的性能表現差異,同時也為減少橢圓孔優化時的變量維度,本文以逐步優化的形式先后開展了圓形孔優化與橢圓孔優化,其中圓形孔優化獲得的軸向與徑向偏轉角在橢圓孔優化中保持恒定。

3.1 圓形孔優化

對圓形孔開展優化,采用拉丁超立方采樣方法建立80個初始樣本,包含更新迭代共預設了98個優化樣本。采用交叉驗證方法重構Kriging代理模型并對驗證點進行預測,以預測值與實際值的差值評價Kriging代理模型預測的準確性,驗證結果如圖7所示。可以看出,驗證點整體分布在中心線附近,特別是最優值點附近(左下角的驗證點)的實際值與預測值符合較好,說明預測精度位于較高的水平,可以認為響應面已捕捉到了設計空間的整體特征,圓形孔的優化結果具有較高可信度。

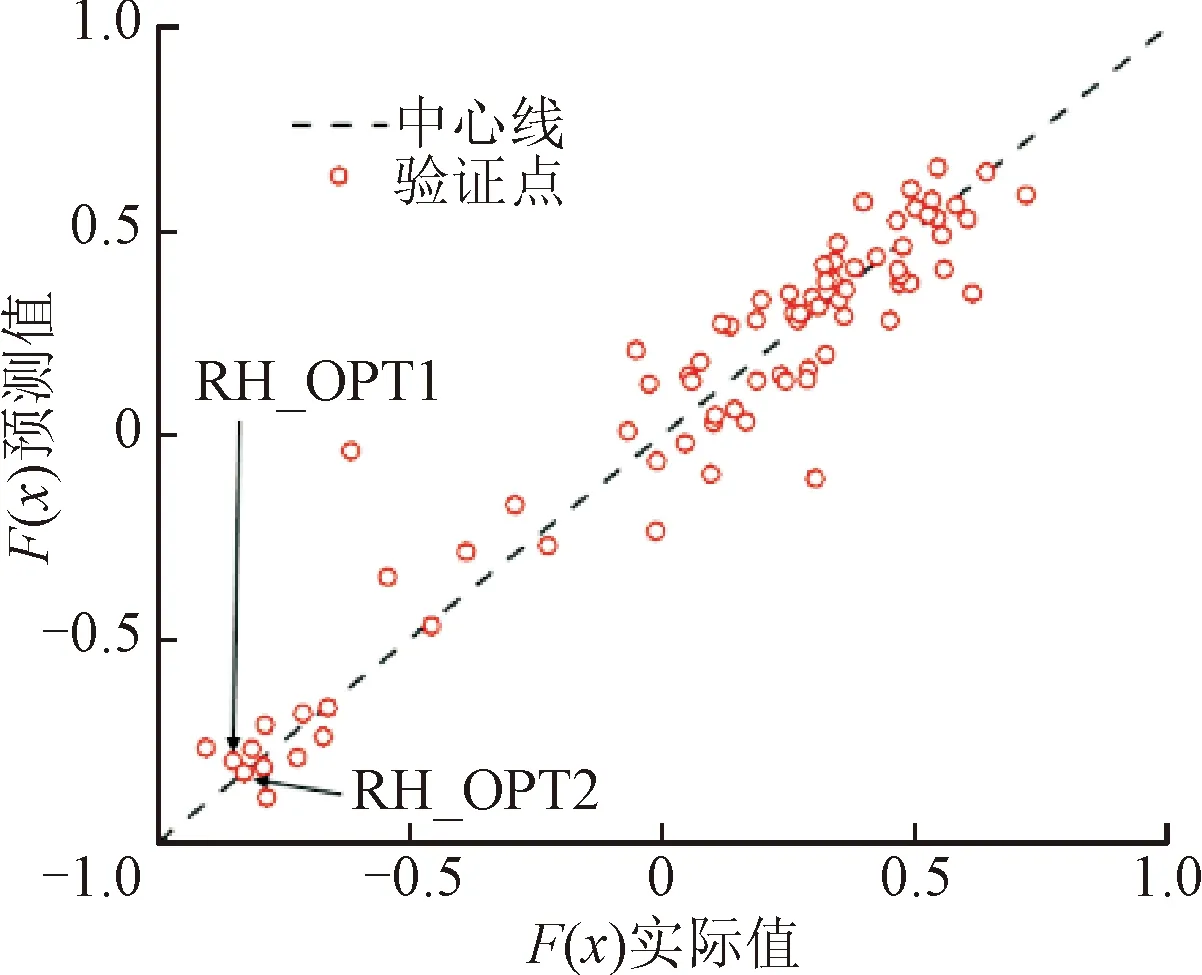
圖7 圓形孔優化設計交叉驗證Fig.7 Cross validation for round hole optimization

在圓形孔的優化工程中獲得了兩個具有較高性能的優化結果,即圖7中的RH_OPT1與RH_OPT2,對應的幾何結構如圖8所示。可以發現,兩種優化結構均大量采用了負徑向偏轉與正軸向偏轉的冷卻孔組合方式,僅有第一冷卻孔的徑向偏轉方向存在區分,其設計參數如表5所示。

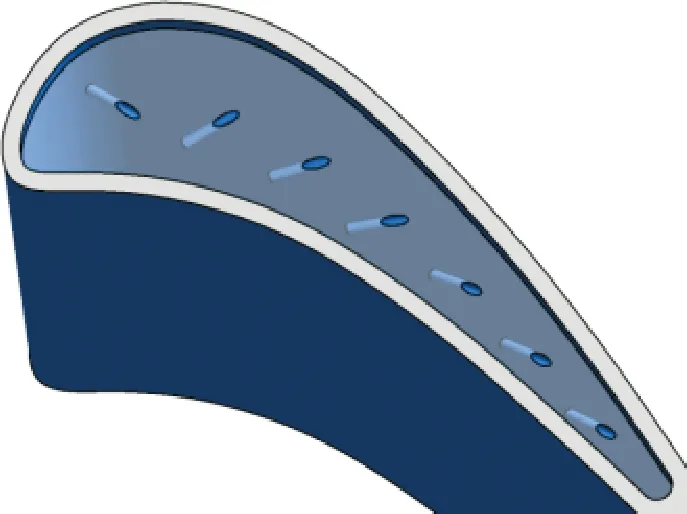
(a)RH_OPT1

(b)RH_OPT2

表5 圓形孔優化結構參數

以無偏轉角的圓形冷卻孔作為參考結構(RH0),對比了葉頂射流的流線分布,如圖9所示。可以看出,在無偏轉結構中,雖然冷卻射流受凹槽渦影響向壓力面側肩壁出流,但流線的軸向移動距離有限,導致在吸力面肩壁的出流位置靠前。在優化結構RH_OPT1、RH_OPT2中,大角度的軸向偏轉保持了流線的貼壁性,延長了射流的軸向覆蓋范圍,增強了冷卻流下游的堆積,射流的肩壁出流位置集中在凹槽尾緣。此外,流線還依靠負徑向偏轉擴大了軸向移動的轉折角,使中弧線附近區域得到了流線包覆。RH_OPT1結構由于第一冷卻孔未采用負徑向偏轉結構,導致其孔后流線包覆范圍相對較窄,但流線貼壁性的提高使其在肩壁的出流位置相對靠后。

(a)RH0

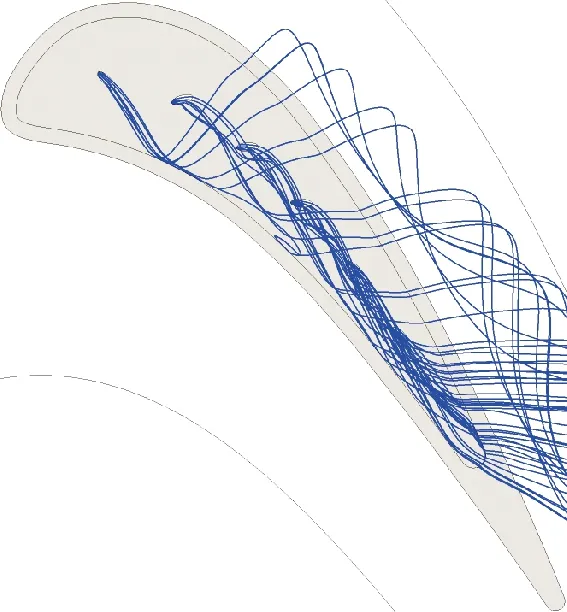
(b)RH_OPT1

(c)RH_OPT2

圖10對比了前緣泄漏流再附著位置、冷卻孔及孔后位置的流向渦量分布。參考結構RH0僅在尾緣區域能觀測到較高的孔后射流渦量,但仍相對集中分布在壓力面側,同時也能觀測到顯著的壁面射流渦脫離現象。相對于參考結構,可以發現優化結構RH_OPT1、RH_OPT2由于擴大了流線覆蓋范圍并增大了軸向傾角,使射流的出流高度降低,射流渦分布更寬,凹槽尾緣射流渦與壁面的貼附也保持較好。RH_OPT1中第二冷卻孔孔后角渦渦量增大,說明在正徑向、正軸向組合偏轉冷卻孔影響下前緣射流保持了良好的貼壁性能。RH_OPT2的第一冷卻孔由于采用了負徑向偏轉,孔后射流渦受凹槽渦影響分布相對分散,同時在第二冷卻孔截面上部的刮削渦有一定增大,反映了射流流線在此處與泄漏流的摻混加劇。

(a)RH0

(b)RH_OPT1

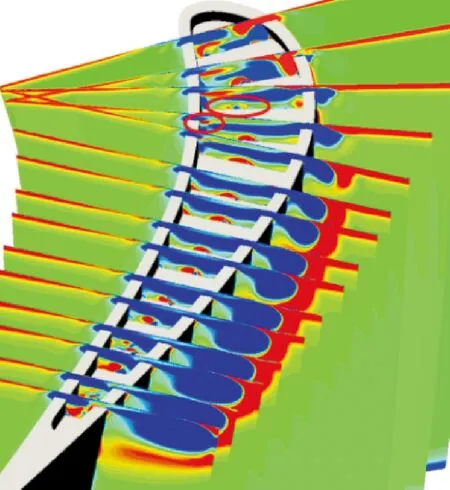
(c)RH_OPT2

圖11展示了凹槽葉頂絕熱氣膜冷卻效率η分布與橫向平均氣膜冷卻效率對比,RH0、RH_OPT1、RH_OPT2的葉頂平均氣膜冷卻效率分別為0.019 259、0.083 147、0.088 267。可以看出,參考結構RH0由于氣膜抬升導致孔后氣膜覆蓋范圍與冷卻效率顯著降低,優化結構RH_OPT1與RH_OPT2在保持較好氣膜貼壁性的同時依靠負徑向偏轉擴大了孔后氣膜覆蓋范圍,顯著提升了氣膜冷卻效率,凹槽尾緣的氣膜冷卻效率依靠較好的流線堆積效應也有大幅增加。RH_OPT1的前緣氣膜冷卻效率略低于RH_OPT2結構,但在下游略有增長,原因是RH_OPT2雖然依靠第一冷卻孔的負徑向偏轉擴大了氣膜覆蓋范圍,但也削弱了下游的流線堆積,RH_OPT1則保持著較好的氣膜貼壁性,從而提高了下游的冷卻效率。

(a)RH0

(b)RH_OPT1

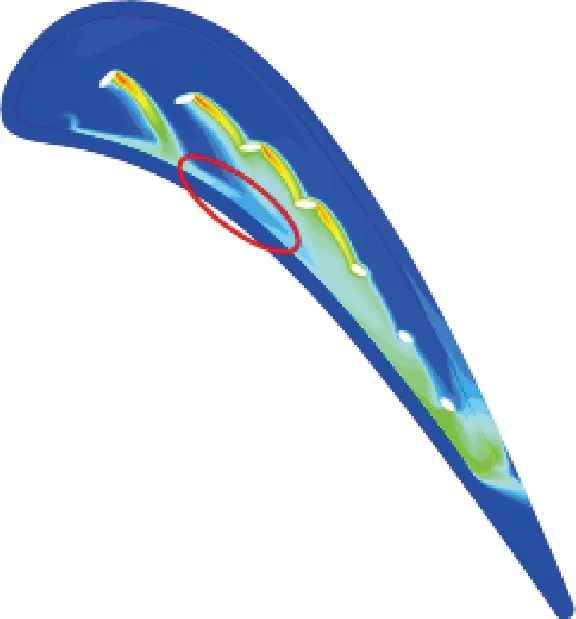
(c)RH_OPT2

(d)橫向平均氣膜冷卻效率

圖12對比了凹槽底面的換熱系數分布與橫向平均換熱系數,RH0、RH_OPT1、RH_OPT2的平均換熱系數分別為649.748、648.971、636.325。可以看出,參考結構RH0中射流受凹槽渦影響向壓力面側肩壁出流,使低換熱系數區分布在壓力面側。優化結構依靠冷卻孔的負徑向偏轉增大了射流出流的轉折角,擴大了低換熱系數區域范圍,并有效降低了中弧線附近的換熱系數,但凹槽前緣冷卻孔的壓力面側區域由于缺少氣膜包覆出現了局部換熱惡化,其中優化結構RH_OPT2擴大了前緣區域的氣膜覆蓋范圍,顯著降低了前緣橫向平均換熱系數。

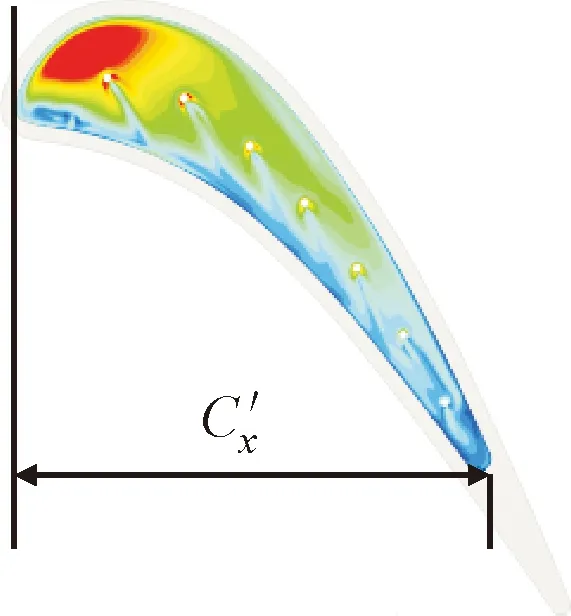
(a)RH0

(b)RH_OPT1

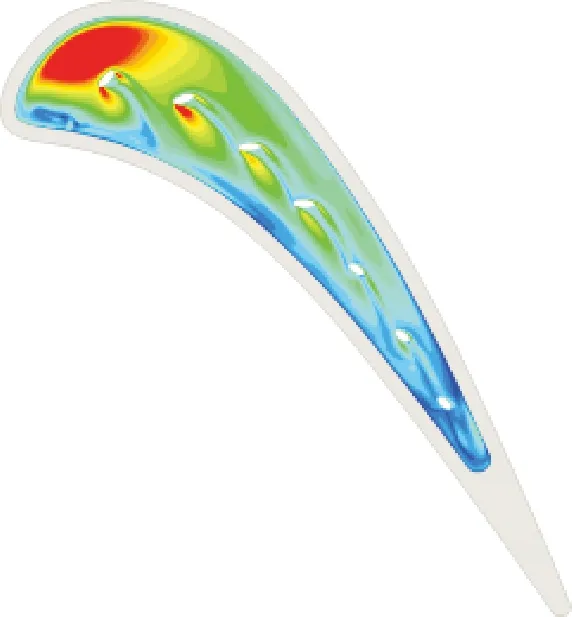
(c)RH_OPT2

(d)橫向平均換熱系數

圖13對比了凹槽葉頂泄漏流總量與主流之比,以及泄漏流占比沿軸向弦長的分布。可以看出,優化結構中由于保持了良好的射流貼壁性,有效減弱了射流渦強度,使泄漏流量從凹槽中后部開始逐步下降,同時在凹槽尾緣由于射流的堆積效應導致射流集中出流,形成的大尺度刮削渦阻塞了通流狀態的葉頂泄漏流,大大減小了凹槽尾緣的泄漏流量。RH_OPT2由于前緣采用了負徑向偏轉,大角度的流線翻轉使第一冷卻孔的射流渦得到了一定程度發展,導致了前緣區域的泄漏流量略微增長。

(a)泄漏流量整體變化

(b)泄漏流量沿軸向弦長分布

3.2 橢圓孔優化

從圓形孔優化結果的對比可以看出,RH_OPT2冷卻、換熱性能較優于RH_OPT1,但RH_OPT1氣動性能更為優秀,而橢圓孔具有大寬高比的優勢,結合氣動性能最優的優化結果能獲得更好的綜合性能,所以在橢圓孔優化研究中,將以RH_OPT1模型的軸向、徑向偏轉角為基準,以橢圓孔替代圓形冷卻孔,開展自偏轉角優化研究,設計變量如前文表3所示。

橢圓孔優化研究共設置90個優化樣本,初始樣本為60個,交叉驗證結果如圖14所示。由于式(3)中選用的參考值變更為橢圓孔參考結構的計算結果,所以導致目標函數的分布范圍有所變化。可以看出,驗證點整體分布相對集中并靠近中心線位置,可以認為優化結果具有較高可信度。

圖14 橢圓孔優化交叉驗證Fig.14 Cross validation for oval hole optimization

圖15展示了橢圓孔參考與經過優化得到的最優解結構的三維模型。參考結構OH_REF僅將RH_OPT1的孔型替換為橢圓孔,自偏轉角度均為0°;優化結構OH_OPT調整了射流的出流方向,除第一冷卻孔外均減小了橢圓孔短軸與中弧線切線間的夾角,OH_OPT的自偏轉角參數如表6所示。

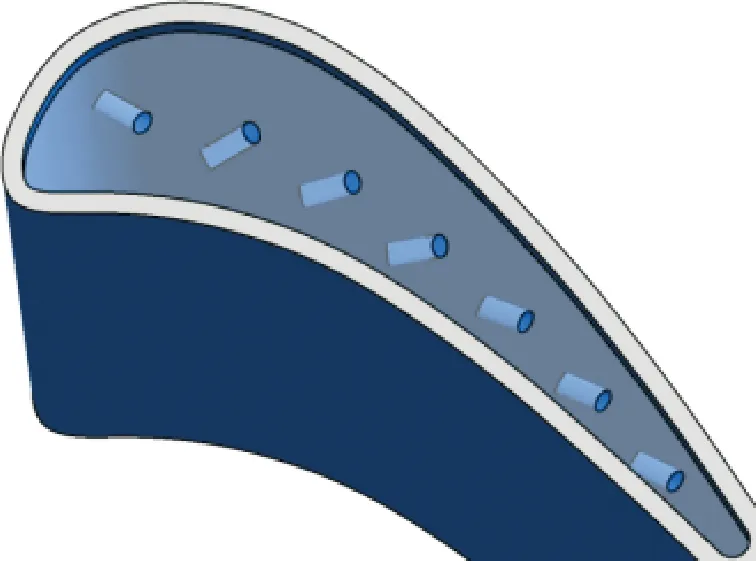
(a)OH_REF

(b)OH_OPT

表6 橢圓孔優化結構參數

圖16對比了優化結構的射流流線分布。可以看出,OH_REF相比RH_OPT1擴大了第一冷卻孔射流氣膜的覆蓋范圍,并且在凹槽尾緣可以觀測到部分流線的匯聚及出流,OH_OPT則進一步增強了凹槽下游的流線堆積效應,同時射流在肩壁的出流位置向尾緣方向收縮,凹槽尾緣匯聚及出流的流線顯著增加。

(a)RH_OPT1

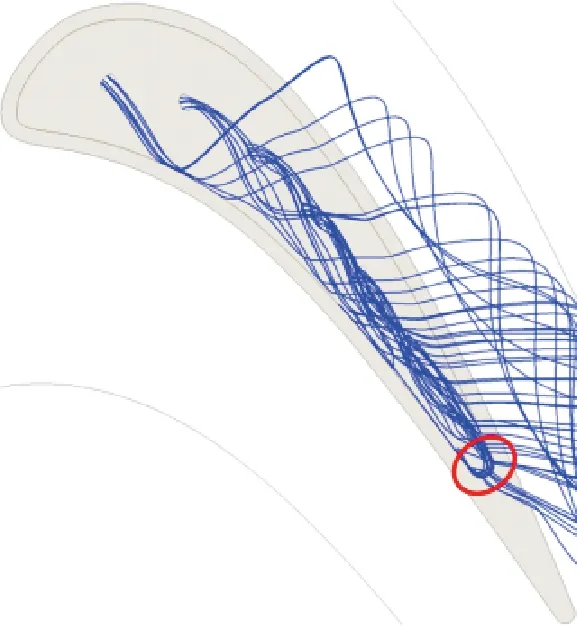
(b)OH_REF

(c)OH_OPT

圖17對比了橢圓孔優化結構的流向渦量分布。可以看出,OH_REF與RH_OPT1的前緣及中部射流的渦量分布相似,均具有較寬的射流覆蓋范圍及較低的射流高度。在RH_OPT1的凹槽近尾緣區域,可以看到位于肩壁的出流轉向渦,而OH_REF、OH_OPT該處的渦量顯著減小,說明橢圓孔結構的貼壁性能相對優于圓形孔結構,使射流保持了軸向移動從而減小了近尾緣肩壁的出流流量。優化結構OH_OPT由于調整了射流角度,相對OH_REF進一步提高了射流的覆蓋范圍并降低了射流高度。在凹槽尾部截面對比中,可以看到OH_OPT射流渦與上游射流渦的融合,表明OH_OPT在凹槽下游具有更優的冷氣貼壁性能。

(a)RH_OPT1

(b)OH_REF

圖18對比了橢圓孔優化結構的氣膜冷卻效率分布及橫向平均氣膜冷卻效率,RH_OPT1、OH_REF、OH_OPT的平均氣膜冷卻效率分別為0.083 147、0.115 504、0.128 092。可以看出,OH_REF、OH_OPT結構在不依靠冷卻孔負徑向偏轉的情況下顯著擴大了前緣的氣膜覆蓋范圍,且高氣膜冷卻效率區的范圍也顯著提升。這是由于橢圓孔依靠低曲率的出流邊提高了氣膜的貼壁性能,擴大了冷卻孔出口的氣膜覆蓋范圍。橢圓孔結構的凹槽尾緣也由于較好流線堆積效應提高了氣膜冷卻效率。圓形孔結構由于具有較大的冷卻孔出口形變,可以依靠橫向流擴大氣膜覆蓋范圍,而OH_REF中橢圓孔由于出口形變較小導致中部冷卻孔的射流偏角過大,不利于氣膜覆蓋范圍與冷卻效率的提升。OH_OPT在OH_REF的基礎上調整了射流與橫向流的夾角,進一步提高了凹槽中部的氣膜覆蓋范圍與冷卻效率。

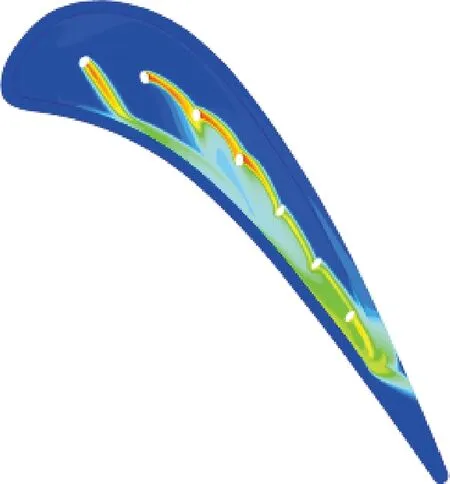
(b)OH_REF

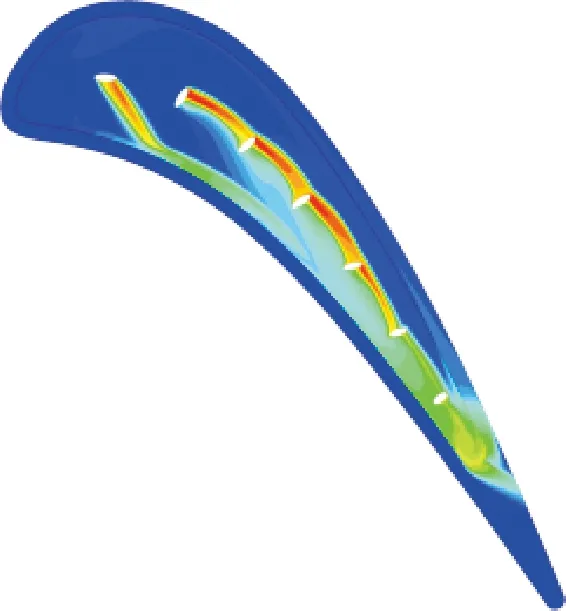
(c)OH_OPT

圖19對比了凹槽底部的換熱系數分布與橫向平均換熱系數,RH_OPT1、OH_REF、OH_OPT的平均換熱系數分別為648.971、664.95、657.116,計算前70%區域的換熱系數分別為755.900、755.530、753.075。可以看出,橢圓孔結構在凹槽尾緣存在大量流線累積,促進了尾緣射流的貼壁性能進一步提升,形成的渦系結構破環了凹槽尾緣的邊界層發展,導致了換熱系數的上升。但是,凹槽尾緣屬于低換熱系數區,在實際工作環境下對熱防護的考量比重較小,而橢圓孔優化結構OH_OPT則在凹槽前、中部高換熱系數區域的促進了孔后換熱系數的降低,具有較高的工程價值。

圖20對比了橢圓孔結構的葉頂泄漏流量。可以看出,泄漏流量的整體變化較小,橢圓孔及優化結構在RH_OPT1的基礎上保持了泄漏流量的下降趨勢。對圖20(b)分析可以發現,橢圓孔結構進一步提高了凹槽下游的流線堆積效應,導致了射流對泄漏流的阻塞作用增強,凹槽尾緣的泄漏流量下降,OH_OPT則是在OH_REF的基礎上對凹槽尾緣的阻塞作用有微弱提升,進一步降低了凹槽尾緣及后肩壁的泄漏流流量。

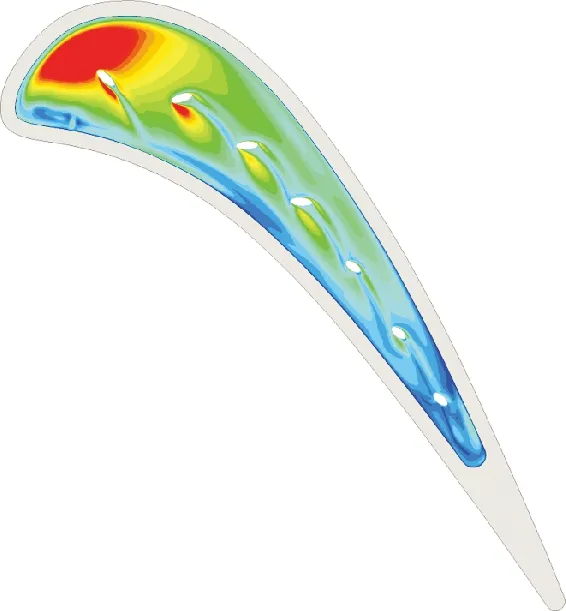
(a)RH_OPT1

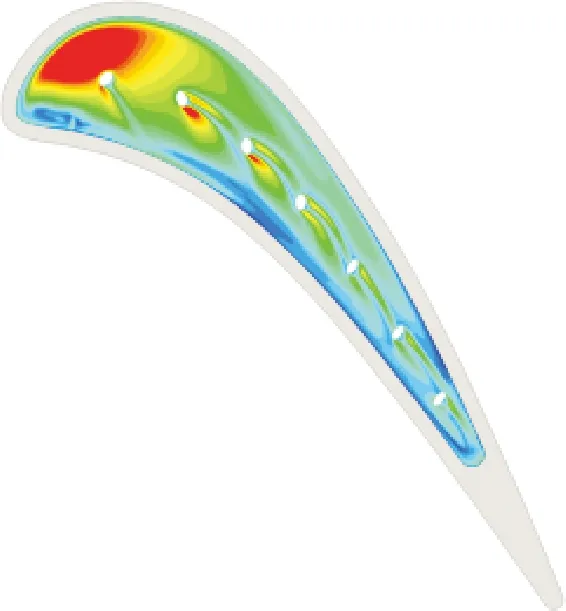
(b)OH_REF

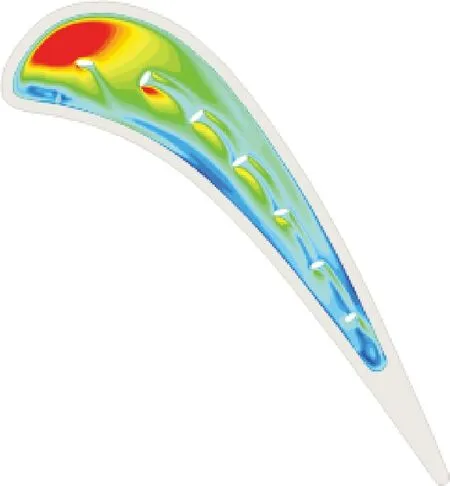
(c)OH_OPT

(d)橫向平均換熱系數

(a)泄漏流量整體變化

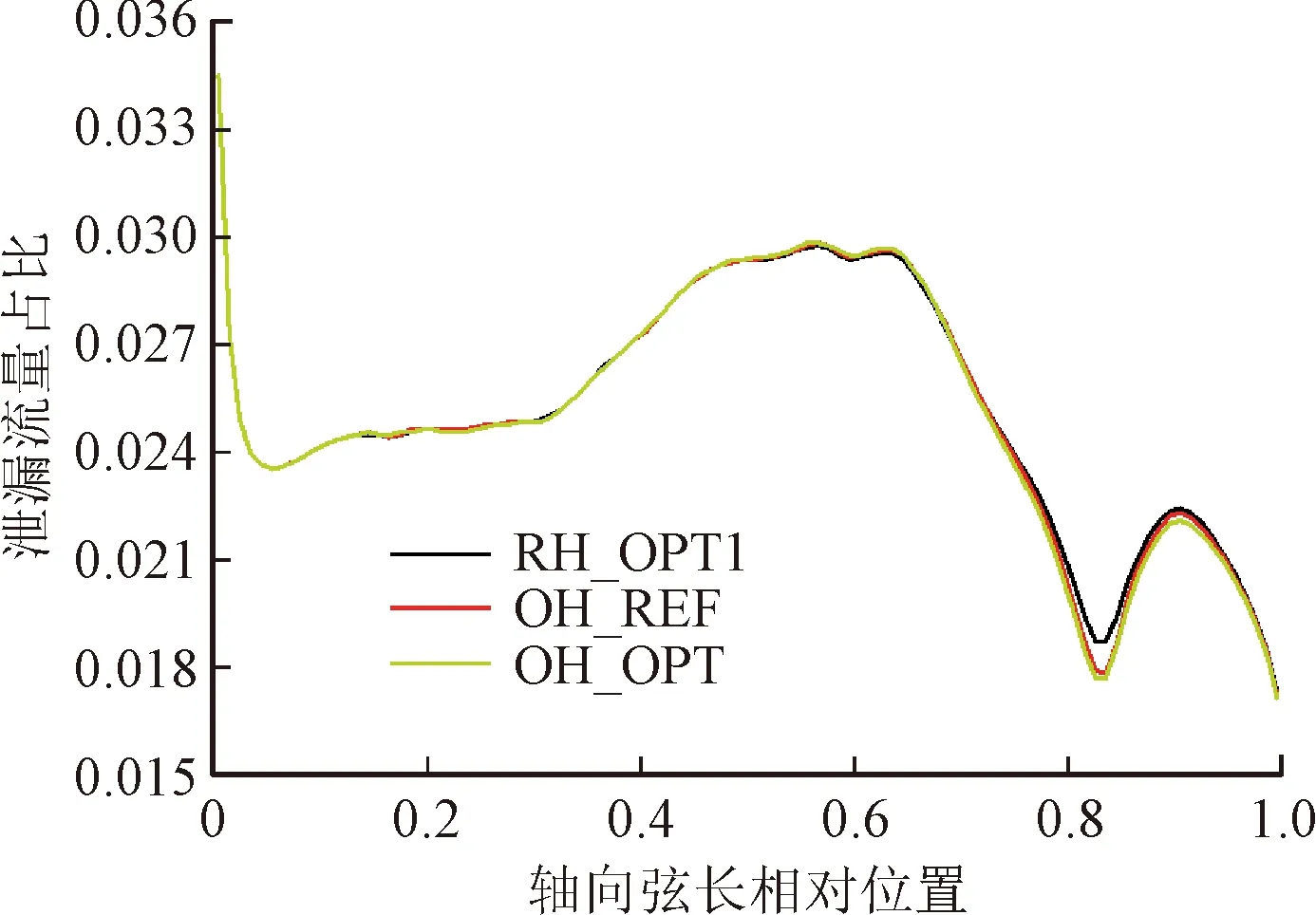
(b)泄漏流量沿軸向弦長分布

表7對比了優化前后各結構的性能參數,優化目標為冷卻效率與泄漏流量。可以看出,針對凹槽葉頂冷卻孔偏轉角的優化有效提升了冷卻效率并降低了泄漏流量。橢圓孔優化結構相比圓形孔進一步提升了冷卻性能與泄漏流控制效果,但由于干擾了凹槽尾緣的邊界層發展,導致了換熱系數上升。

表7 性能參數對比

3.3 變吹風比工況校核

為進一步校核優化結構在變工況環境下的冷卻與氣動性能,研究了各優化個體在吹風比M=0.5,1.0,1.5時的葉頂平均氣膜冷卻效率及泄漏流占比的變化情況。圖21展示了變吹風比工況下葉頂平均絕熱氣膜冷卻效率的變化情況。可以看出,變工況中各優化結構及參考結構的氣膜冷卻效率變化趨勢保持一致,吹風比增長至1.5后出現了氣膜分離現象,導致了葉頂平均冷卻效率的下降。變吹風比工況中,優化結構的氣膜冷卻效率在參考結構的基礎上依舊保持著較高的增長率,特別是OH_OPT在橢圓孔及組合偏角的影響下,大幅擴張了氣膜覆蓋范圍并提高了貼壁性能,使其在變工況環境中保持著較高的冷卻效率,并在低吹風比下展現了最高的增長斜率。

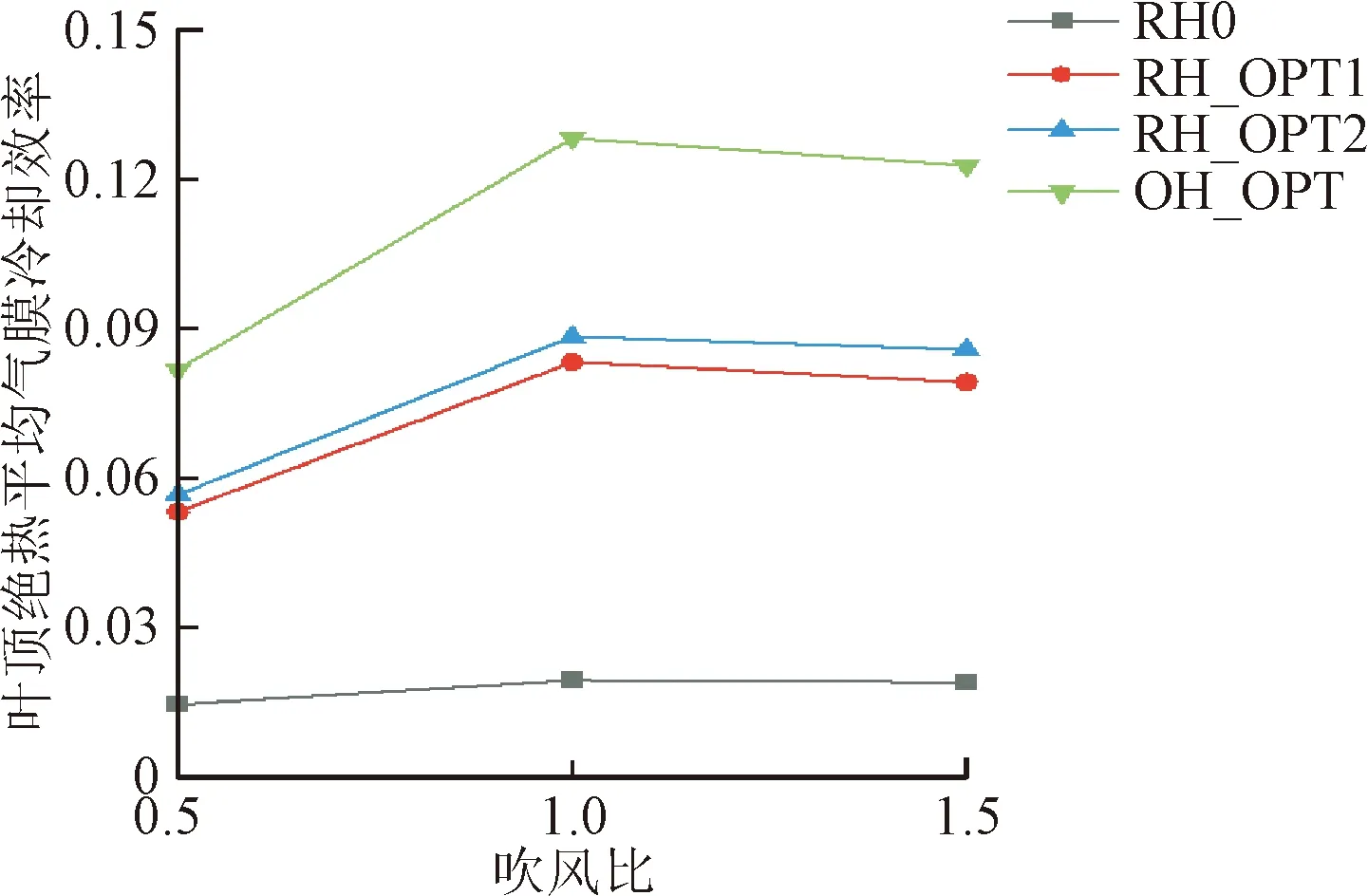
圖21 變工況氣膜冷卻效率對比 Fig.21 Comparison of film cooling effectiveness in variable operating conditions

圖22對比了不同吹風比下泄漏流量占比的變化情況。可以看出,優化結構及參考結構的泄漏流量變化趨勢保持一致,且隨著吹風比的增加,由于葉頂射流的阻塞效應逐步增強,泄漏流量占比有顯著降低。相同吹風比下,優化結構的泄漏流量顯著低于參考結構,且該差值隨著吹風比增加而逐步提升,其中OH_OPT在優化結構中保持著最低的泄漏流量占比。

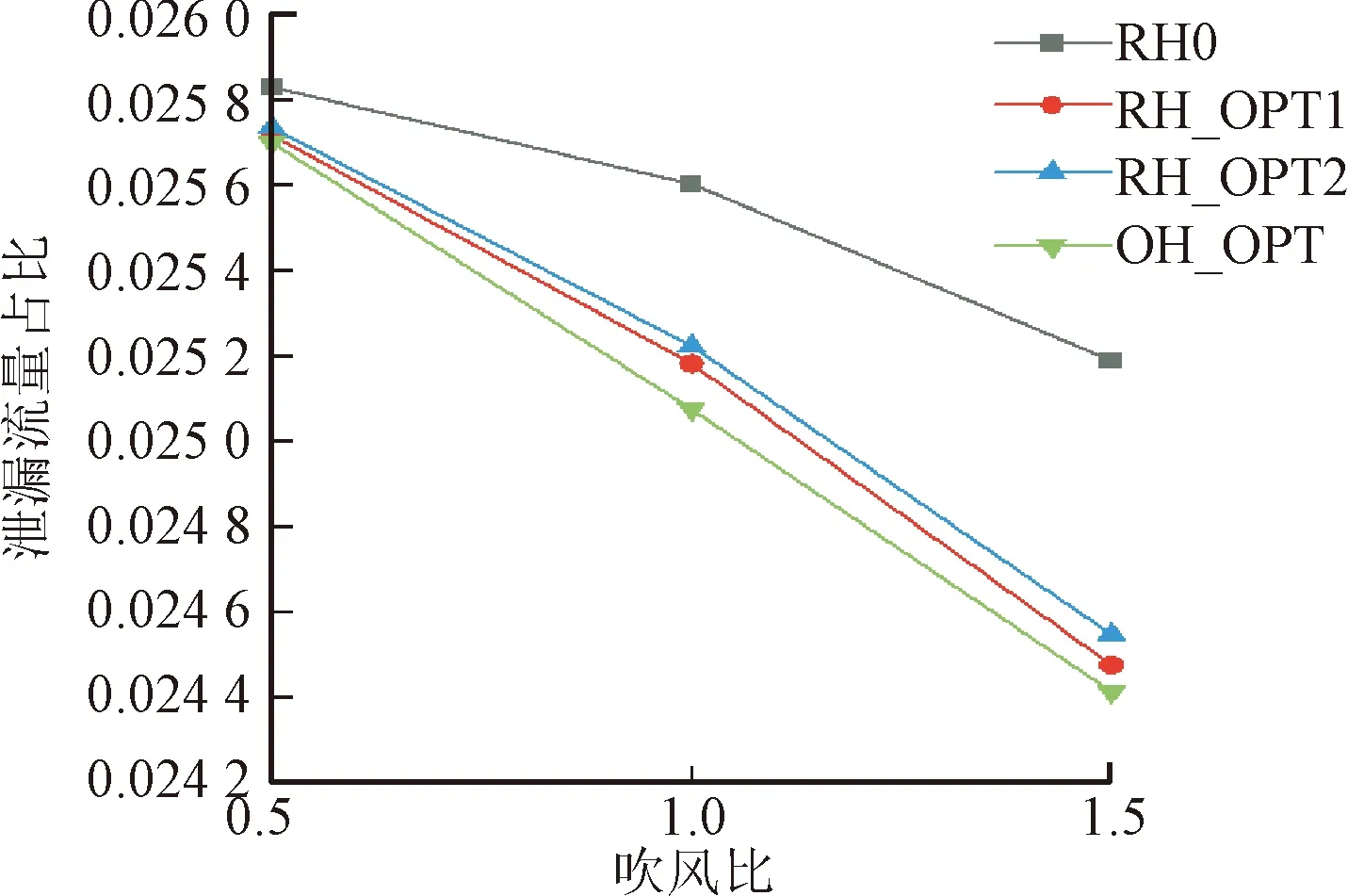
圖22 變工況泄漏流量對比 Fig.22 Comparison of leakage flow in variable operating conditions

4 結 論

本文采用數值方法研究了凹槽葉頂冷卻孔組合偏轉角對氣熱特性的影響,基于Kriging代理模型、結合EI加點準則的優化算法,首先對圓形冷卻孔進行了組合偏轉角優化,再以獲得的組合偏轉角為基礎開展了橢圓冷卻孔自偏轉角優化,獲得的主要研究結論如下。

(1)本文提供了一種適用于凹槽葉頂的圓形孔及橢圓孔組合偏轉角參數化方法,設計了徑向偏轉角、軸向偏轉角、橢圓孔自偏轉角等多個優化變量,該方法參數變化靈活、特征指定明確,參數與結構間具有一一對應關系,適合開展優化設計工作。

(2)圓形孔優化中,采用負徑向偏轉與正軸向偏轉的組合偏轉結構能在提高氣膜冷卻性能的同時保持氣膜的貼壁性能,進而同時提高了凹槽葉頂的換熱與氣動性能,圓形孔優化結構RH_OPT2相比無偏轉圓形孔結構RH0的氣膜冷卻效率提高了358.3%。同時,組合偏轉射流減小了凹槽前、中部射流渦尺度,增強了凹槽下游的射流阻塞效應,其中RH_OPT1泄漏流量相對減少量達到了1.641%。

(3)橢圓孔短軸方向與主流間保持小角度的夾角能較大程度的提升氣膜冷卻效率,橢圓孔優化結構OH_OPT相比RH0的氣膜冷卻效率提升了565.1%。橢圓孔射流凹槽下游的流線堆積增強,提升了射流阻塞效應,泄漏流量相對RH0減少了2.063%。

(4)橢圓孔相比圓形孔的出口孔周曲率更小,能有效提高射流的貼壁性能,促進氣膜覆蓋的擴大與冷卻效率的提高,同時橢圓孔增加了自偏轉角這一設計變量,擴展了設計空間維度,能通過優化設計進一步提高葉頂的氣熱性能。

(5)通過變吹風比工況校核可以發現,優化結構在低、高吹風比及設計工況中均可以獲得較高的冷卻、氣動性能,證明了優化結構相對于參考設計的優越性及優化設計方法的可靠性。