精選學材，引發學生思維自然生長

福建武夷山市興田中心小學 （354305） 余麗平

福建武夷山市興田中心小學 （354305） 王盛忠

一、起點準確的學材讓思維“扎根”

學生思維的種子只有在已有經驗土壤中才容易“扎根”。數學知識層層遞進、螺旋上升，教師要結合學生的已有經驗，確定學材，讓學生能夠在原有知識的基礎上更進一步。

例如，三年級教材中“認識分數”內容直接圖示一盤桃子，要求把這盤桃子平均分給4 只小猴，并求出每只小猴分得這盤桃子的幾分之幾。筆者在教學時，先將教材資源拓展為適合學生的學習資源（如圖1-1）：設置了小猴過生日，邀請了3位好朋友來吃生日蛋糕的情境，并提問怎樣把這個蛋糕平均分給4 只小猴呢？每只小猴分到這個蛋糕的幾分之幾呢？為什么可以用表示？在學生對這些問題有一定了解后，再出示教材中的一盤桃子（如圖1-2），讓學生分一分，涂一涂。

圖1-1 “認識分數”教材資源拓展

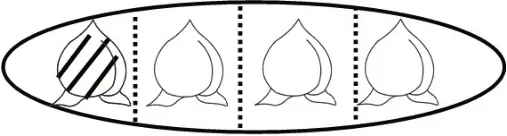
圖1-2 “認識分數”教材圖示

數學知識的教學，要注重知識的生長點與延伸點。學材的設計也應注意研究學生的已有知識經驗對新知學習的影響，研究新知的起點。如果教師直接出示教材中的情境圖，學生自然會想到每只小猴分到1 個桃子，并沒有考慮用分數表示。因此，需要有連接作用的學習資源充分喚醒學生的已有經驗，通過引入的情境，從“每只小猴吃了一個蛋糕的”過渡到“吃一盤桃子的”，自然引出分數。

再如，教學“圓的認識”一課時，教材創設學生熟悉的套圈游戲情境，讓學生去思考套圈時三種站法的公平性。通過生活經驗，學生很容易得出以玩具熊為中心，圍成一個圓的形式是最公平的。這恰恰是圓的本質——圓的中心到圓上任何一點的距離都相等。課上“投石入水”的情境，蕩開的一圈圈波紋都是圓形的，這是生活常識，但其中的道理卻少有人去關注或深入研究。因而在教學“圓的認識”時，筆者便圍繞水的波紋形狀展開，讓學生去思考為什么蕩起的波紋是圓形的。以石子入水的地方為圓的中心，水面上的波紋以同樣的速度向四周擴展，形成了一個個圓。通過思考這個自然現象，學生再一次感受圓的本質。

二、啟迪思考的學材讓思維“萌芽”

提供產生問題溫床的學材，利于學生發現和提出問題，讓學生的思維順利“萌芽”。學生主動思考并積極提問，才能激發學習的活力，激起探索發現的欲望。例如，在教學“平年和閏年”一課，教師充分尊重學生的問題，以問題驅動來展開學習，這更易燃起學生的學習熱情。

生1：為什么會有平年和閏年？

師（演示）：地球繞太陽轉一周的時間是1 年，但是精確的時間是365 天5 小時48 分46 秒。為了方便記憶，人們將整天數365天規定為1年，余下的時間約為每四年積累一天。

生2：公歷年份是4的倍數的一般是閏年，那有沒有特殊情況？

教師提供1897年～1904年的二月月歷（如圖2）讓學生自己判斷。

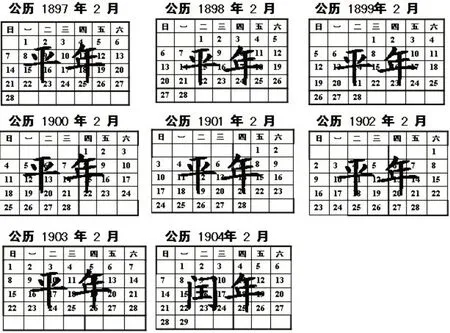
圖2 1897年～1904年的二月月歷

生3：1900年為什么不是閏年？

師：我們把5 小時48 分46 秒看作6 小時，1 年就多算了11 分14 秒，可別小瞧了這11 分14 秒，日積月累，400年過去了，差不多要多出來3天呢！多了3 天也不行，得想辦法拿掉啊。于是規定，從每相鄰的4 個整百年份中，拿掉3 天。例如，1700 年、1800 年、1900 年、2000 年，我們把1700 年的2 月29日拿掉，變成了平年；1800 年也拿掉1 天，也是平年；1900 年拿掉1 天，也是平年；3 天拿完了，那么2000 年就是閏年。也就是說，整百年份必須是400的倍數的才是閏年。

在教學中，平年和閏年看似是比較枯燥的內容，判斷方法也比較簡單。教師以平年和閏年產生的知識背景為學材，鼓勵學生問“為什么”，以“為什么”推動教學，既鼓勵學生提問，也保證學生在感興趣的學材中對數學知識理解更透徹。

三、層層遞進的學材讓思維“拔節”

教師除了要準確把握每節課的重點和難點，還應換位思考，找出學生在學本課的內容時容易出錯的地方和困惑點，結合學生的情況提供學材。

例如，在“分數的初步認識”的教學中，學生認識了把4 個桃子平均分給4 只小猴，每只小猴分得這些桃子的。但是這個表示的是將整體平均分成4 份，其中1 份恰好是1 個桃子，如果從整體分得的是2 個桃子呢？學生是否能理解？因而對于中的“1”是表示1 份，學生的理解還是模糊的。因此，教師又給學生設計了一個學習情境：將8 個桃子平均分給4 只小猴，每只小猴分得這些桃子的幾分之幾呢？教師引導學生分析得到，將8 個桃子平均分成4份，每份有2個桃子。

為了展現知識的本質，教師讓學生進行第三次分桃子：將12 個桃子平均分給4 只小猴，每只小猴分得這些桃子的幾分之幾？這次學生很快就說出每只小猴分得這些桃子的。

學生三次分桃子的過程是對自己原有經驗的不斷調整和擴充的過程，1 個桃子是4 個桃子的比較直觀，學生比較容易接受。2 個桃子是8 個桃子的，學生要把2個桃子的具體數量轉化為份數，2 個也是1 份，需要形成新的知識結構，用份數的眼光來觀察部分與整體的關系。第三次分桃子，學生能用新的經驗來處理問題。可見，學生的學習是在已有經驗上，擴充新知在相同或類似的情境中遷移概括，在原有知識結構上不斷充實自己的結構，實現思維的“拔節”。

再如教學“角的度量”時，教師可精心設計如下層層遞進的學材：猜一猜，下面的角可能是多少度？第一題：角的一條邊指向量角器左邊的40 度，另一邊不給出。第二題：角的一條邊指著量角器左邊60 度，另一邊暫不給。第三題：角的一條邊指著量角器左邊70 度，另一邊暫不給。第四題：角的一條邊指著80 度，另一邊暫不給。這樣的學材設計折射出教師靈動的教學思維，蘊含著豐富的數學思考。學生在一波三折的思維波瀾中不斷經歷著認知結構的失衡與平衡，在成功突破“角的度量”的認知難點同時，思維能力也在不斷提升。

四、形象直觀的學材給思維“澆水”

形象直觀的學材可以在學生困惑時提供感悟的營養，給思維這棵大樹“澆水”。教師應從一個概念的不同方向，和解決問題的不同途徑，引導學生靈活理解數學知識。

例如，教學“認識小數”一課時，筆者從標價牌引入。

師：這三個數是小數，大家在生活中見過嗎？

生1：0.5 元就是5 角，0.8 元就是8 角，1.2 元就是1元2角。

師：小數和分數有關系嗎？

學生在生活中經常看見小數，也認識小數，最常見的就是以元為單位，用小數表示的標價牌。因此，標價牌對學生來說就是最直觀、熟悉的學材。尊重學生的原有認知，讓他們用自己的方式理解，也將認識小數和小數的大小比較銜接起來。

再如，在教學“長方形和正方形的周長”時，學生計算長方形周長大多用長乘2，寬乘2，然后相加的方法。很多學生不太喜歡用先算一個長與寬的和，再乘2 的方法。這是因為學生缺乏直觀的長方形表象。教學中，營造直覺思維情境，可以引導學生運用自己的手指，圍成一個長方形（如圖3），再拿開一只手，通過兩只手的拼與分，學生直觀感悟到周長就是兩個長與寬的和。

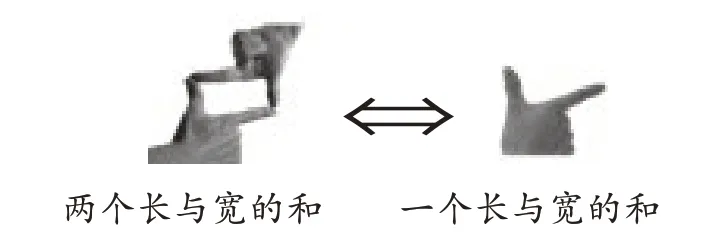
圖3 手指圍成長方形的長和寬

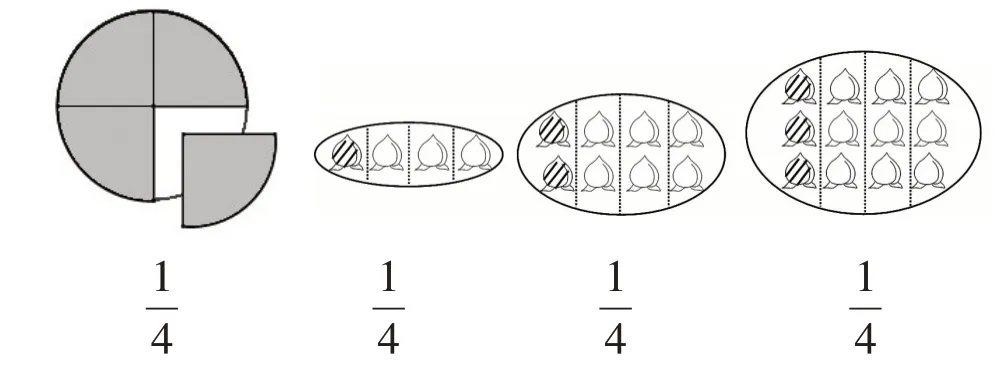
圖4 “認識分數”學習資源

形象直觀的學材讓抽象的知識形象化，讓所學內容看得見、摸得著。在這種有趣、現實的情境中，學生基于聯系觀的直覺發現，豐富了體驗過程，培養了數學思維能力。

五、比較辨析的學材促思維“開花”

比較辨析的學材可以催生學生思維之花綻放。比較是把一些事物的個別屬性加以分析，而后確定它們之間異同點的邏輯思維過程。在充分體驗的基礎上，學生不再是就題看題，而是將相關聯的一組題目進行比較，讓比較成為常用的思考方式。

例如，在“認識分數”教學中，筆者引導學生對本節課所用的學習資源進行回顧總結。

生1：平均分一個物體，每份都是一塊一塊的，不是一整個。平均分一個整體，每份可能是一個或者幾個。

生2：把一個物體平均分成幾份，其中的一份可以用幾分之一表示。

生3：把一個整體平均分成幾份，其中的一份也可以用幾分之一表示。

在學習本課的基礎上，提供學材將其和原有知識進行比較，引導學生將本課的新知自覺納入已有知識結構中，讓學生從更高層次理解分數的意義。

六、總結提升的學材讓思維“結果”

提升的學材讓學生獲得的知識更加飽滿。在數學概念和方法間建立聯系，從不同知識點的簡單聯系，到不同領域的內在聯系，有助于學生將知識有機整合，重新構建。

例如，在教學“分數的初步認識”一課時，教師提供學材讓學生讀一讀，比一比。

①一盤蘋果，我吃了2個，盤子里還有蘋果嗎？

生1：第①題，盤子里面可能有，也可能沒有了。原來只有2 個蘋果，吃了2 個后，就沒有了，如果原來不止有2個蘋果，就還有蘋果。

生2：第②題，盤子里面一定有蘋果，因為是把盤子中的蘋果平均分成2份，吃了其中的1份，所以盤子里面還有1份。

學生接觸了分數后，對于分數到底有什么用，需要更加深刻地理解，筆者提供了兩個問題，讓學生在不同情境的學材中總結出分數的意義，深入思考分數的產生過程，體會分數的作用。

學材是學生學習和教師教學的重要媒介。富含生命力的學材是學生樂意探究、有效學習、提升思維的保證。學材應成為教師預設的重要因素，是教師研究教材，融數學知識、思想方法為一體的產物。有了富含生命力的學材，學生的學習就不是踩著教師的腳印一步一步地前進，而是由學生自己建構，以自己的經驗為背景，來分析知識的合理性，對新知進行分析、總結和歸納，讓學生的思維如種子般獲得自然生長。