試論《事林廣記》與宋元古典管理數學的兩個問題

呂變庭

《事林廣記》的作者陳元靚有可能生活在南宋后期，也有可能“以遺民身份入元”①王珂：《陳元靚家世生平新證》，《圖書館理論與實踐》2011 年第3 期，第60 頁。。據考證，《事林廣記》中的古典數學問題主要分為兩類：算術與數術，前者為《九章算術》系統，后者則為《周易》象數系統。以前學界較少關注《事林廣記》中的數學問題。相較于《事林廣記》中的飲食、樂律、醫學、寓言、繪畫、指南針、釀造、養生等熱門領域而言，迄今尚未見有專論《事林廣記》數學問題的研究成果，人們之所以忽視《事林廣記》中的數學問題，不是說它所記載的數學內容不重要，也不是說它除了重復前人的東西，幾乎沒有增加任何新的思想元素，因而不值得去做研究，而是說它僅僅是一部“日用百科全書類型的中國古代民間類書”②盛博：《宋元古地圖集成》上，星球地圖出版社，2008，第7 頁。，這種文獻性質決定了它的數學內容絕少抽象性，因為它的突出特色就是實用。事實上，“日用之繁”③華羅庚：《數學的用場與發展》，《現代科學技術簡介》，科學出版社，1978，第219 頁。恰恰是數學這門學科的重要特征，現在如此，古代亦復如此。

一、初等算法與胥吏階層的數學管理

中國古代實用數學的發展與秦漢之后胥吏階層的出現有很大關系?！皾h武帝元狩六年（前117 年），在丞相府的382 名官吏中，僅屬吏就有162 名，占官吏總數的42%。”④（日）大庭修：《漢簡研究》，廣西師范大學出版社，2001，第210 頁。這些胥吏都被納入國家官職序列，其所享受的祿秩多少也不等。就他們的職責來說，主要從事日常煩瑣的事務性工作，諸如鄉里治安、賦稅征收、戶籍管理以及公文的抄寫、傳送等。

首先，《事林廣記》載有兩套算術口訣，即“九九算法”和“累算數法”。“九九算法”早在先秦時期就出現了，《管子·輕重戊》云：“虙戲作，造六法（峜）以迎陰陽，作九九之數以合天道，而天下化之?！雹莨苤伲骸遁p重戊》，岳麓書社，1993，第1450 頁?！熬啪胖當怠北M管是一種“薄能”⑥（漢）劉向：《尊賢》，岳麓書社，1993，第600 頁。，但它卻是管理國家的一種有力工具。因此，漢人非常重視“九九之術”，如深圳南頭紅花園發掘的一座漢墓中出土了刻有“九乘”口訣磚⑦深圳博物館：《深圳考古發現與研究》，文物出版社，1994，第232 頁。，揚雄《太玄經》又說：“陳其九九，以為數生?！雹啵h）揚雄：《玄首》，岳麓書社，1993，第2006 頁。此“九九”按照郭金彬先生的解釋：“我國古代九九之術，其含義不僅是乘法口訣，它也是我國古代初等數學的代名詞，是我國古代初等數學的一種簡稱。”⑨郭金彬：《〈周髀算經〉與道》，上?？茖W技術文獻出版社，2018，第160 頁。

其次，“累算數法”是民間對“九九之術”的另一種記憶方法，如果說“九九之術”適用于籌算，那么，“累算數法”則主要用于珠算。但在“累算數法”里，僅見“三三單九”一句口訣，沒有籌算所用數字。因此，明代成書的《盤珠算法》（1573）將《事林廣記》中的“累算數法”命名為“初學累算數法”，表明這個口訣是學習珠算的一道門階?！按缶啪拧彪m然比“小九九”多出了27 句口訣，但在珠算實踐中，民間算家還是非常認可“大九九”的，因為“大九九”對于珠算來說比“小九九”更加方便①華印椿：《中國珠算史稿》，中國財政經濟出版社，1987，第148 頁。?？肌按缶啪拧敝辽僭谀纤螚钶x的《乘法通變算寶》卷既已出現，楊輝曾云：

因九九錯綜而有合數陰陽，凡八十一句，今人求簡，止念四十五句，余置不用，算家唯恐無數可致，豈得有數不用者乎？②（宋）楊輝：《楊輝算法·乘除通變算寶》，河南教育出版社，1995，第1060 頁。

從內容上看，《事林廣記》72 句“大九九”較楊輝所講的81 句“大九九”，僅僅減少了乘數和被乘數都是1 的17 句口訣，然而卻增加了乘數是10 的8 句口訣。一般來說，“大九九”口訣符合乘法的定義，有利于乘法試商，尤其在計算時，無須顛倒乘數與倍乘法的順序，因此，計算速度較快，且不易出現差錯③胡振燦：《珠算技術》，重慶大學出版社，1978，第83 頁。。由此可見，珠算在宋元之際已經開始普及，故朱世杰《算學啟蒙》講到了“九歸除法”口訣，至元二十四年（1287 年）太史院開設算子教學，這應是元朝唯一的珠算教學機構。

除了“小九九”和“大九九”之外，《事林廣記》還載有以下算法：

（一）足數展省，共10 句口訣，是珠算乘法的一種

“足數”是10，故“足數展省”（見圖1）的含義是指從1 到9 每個數字的3 倍之得數是多少。于是，10 句口訣是：一加三，二加六，三加九，四加十二，五加十五，六加十八，七加二十一，八加二十四，九加二十七，十與一同。④（宋）陳元靚：《算法類》，中華書局，1999，第201 頁。

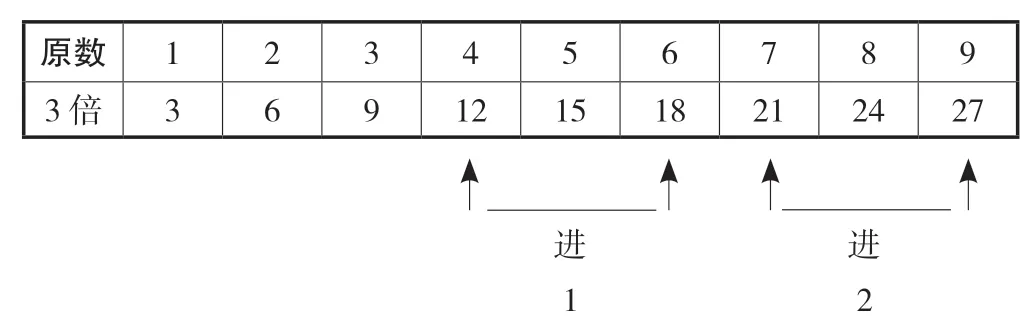
圖1 “足數展省”示意圖⑤孫道義：《速成普及珠算》，中國農業出版社，1998，第75 頁。

可見，“四加十二”的含義就是指前位進一，本位加五；“七加二十一”的含義就是指前位進2，本位加一。

（二）省數歸足，共10 句口訣，是珠算捷法的一種

南宋楊輝在《乘除通變算寶》一書中講了許多“省數歸足”捷法。《事林廣記》具體總結為10種， 即“ 一· 七七， 二· 一五四， 三· 二卅一，四·三一八，五·三八五，六·四六二，七·五卅九，八·六一六，九·六九三，十·與一同”⑥（宋）陳元靚：《算法類》，中華書局，1999，第201 頁。。楊輝舉例云：“銀二百三十七鋌，每鋌二十三兩，問共重幾何？答曰：五千四百五十一兩。術曰：置銀鋌數為實，如省錢歸足七十七法，從尾位損之?！雹撸ㄋ危钶x：《楊輝算法·乘除通變算寶》，河南教育出版社，1995，第1060 頁。對此，華印椿先生用現代數式解釋“省錢歸足七十七法”為：237×23=237×（100-77）=23700-237×77。

（三）置位加減因折法

此法最早見載于《孫子算經》，后來《夏侯陽算經》作了更明晰的表述：“夫乘除之法先明九九。一從十橫，百立千僵，千十相望，萬百相當。滿六已上，五在上方。六不積算，五不單張。上、下相乘，實居中央?！雹啵ㄌ疲╉n延：《明乘除法》，遼寧教育出版社，1998，第1 頁?！妒铝謴V記》則進一步凝練為8 句口訣：“橫千豎百，臥十立一，五不單張，六不積聚。因從上因，折從下折，加從下加，減從上減?！雹幔ㄋ危╆愒n：《算法類》，中華書局，1999，第202 頁。文中“六不積聚”是說“六”這個數字用不著擺六根籌棍，而是用一橫一縱兩根籌棍來表示，“五不單張”則是指5 不能單用一根籌表示，這也就是后來算盤中檔下有五珠的緣由⑩韓慧：《計算機》，中國建材工業出版社，1998，第4 頁。。

二、《事林廣記》對細數、斤秤數和斛粟數等度量衡經濟的管理

“錙銖必較”這個成語首見于宋人陳文蔚的《陳克齋集》，“錙銖”是古代很小的重量單位，“錙”為四分之一兩，“銖”為二十四分之一兩?！妒铝謴V記》載：“算細數長短之法謂之度，起于忽，忽者，蠶口中初出絲也，若有若無。”①（宋）陳元靚：《算法類》，中華書局，1999，第202 頁。具體言之，則十忽成一絲，十絲成一毫，十毫成一厘，十厘成一分，十分成一寸，十寸為一尺，十尺成一丈，四丈為一匹，五丈為一端。②（宋）陳元靚：《算法類》，中華書局，1999，第202 頁。

據《文獻通考》載：“（南宋）時東南諸路歲起綢三十九萬匹，絹二百六十六萬匹，綾羅絁三萬余匹?！雹郏ㄔR端臨：《市糴一》，中華書局，1999，第200 頁。在這上供的背后是民間絲織業的發達，如南宋葉茵《蠶婦吟》：“九日三眠火力齊，五朝又報四眠時。辛勤一月方能繭，繅得成絲卻賣絲。”④（宋）陳起：《葉茵順適堂吟稿·蠶婦吟》，文淵閣四庫全書本。陳旉《農書》曾給湖州一代專以養蠶織絹為生的農戶算了一筆經濟賬，他說：

彼中人唯借桑蠶辦生事，十口之家，養蠶十箔，每箔得繭一十二斤，每斤取絲一兩三分，每五兩絲，織小絹一匹，每匹易米一碩四斗，絹與米價常相侔也，以此歲計，衣食之給極有準的也。⑤（宋）陳旉：《種桑之法篇》，中華書局，1985，第21 頁。

像文中的“每斤取絲一兩三分”，在日?？壗z的買賣過程中應當是經常遇到的問題。因此，南宋秦九韶《數書九章》、楊輝《乘除通變本末》及元代《丁巨算法》都載有不少涉及絲絹斤兩銖的換算題，即反映了這種民間絲絹交易的生活現實。除了“算細數長短之法”，還有“斤秤數輕重之法”?！妒铝謴V記》釋：“斤秤數輕重之法謂之衡，起于黍，黍者輕者末也?！雹蓿ㄋ危╆愒n：《算法類》，中華書局，1999，第202 頁。由于中國古代是用木桿秤來權衡物體的輕重，其中“權”是指秤砣，“衡”是指秤桿，所以“權衡”有時簡稱“衡”，有時也簡稱“權”，二者同義。其計量時以10 黍為基本單位，即“十黍為一絫，十累為一銖，二十四銖為一兩，十六兩為斤，三十斤為一鈞，四鈞為一石”⑦（唐）李淳風：《孫子算經》，遼寧教育出版社，1998，第1 頁。。這是《孫子算經》所采用的衡制，時稱“五權”，但漢代的“五權”比較復雜，存在多種“銖兩之制”。

根據史書記載，宋代的衡制變化比較大，出現了“十有五斤為一秤之則”。如《宋會要輯稿·食貨》之“量衡”載：“御書真、草、行三體淳化錢，較定實重二銖四絫為一錢者，以二千四百得十有五斤，為一秤之則?！雹啵ㄇ澹┬焖奢嫞骸端螘嫺濉罚腥A書局，1957。同時，還出現了“二斤二兩為裹”的衡制。如秦九韶《數書九章》卷17“推求物價”題中有“沉香三千五百裹”⑨（宋）秦九韶：《推求物價》，河南教育出版社，1995，第624 頁。的計量單位，有學者認為，題中的“裹”是指包裹的物品⑩陳信傳：《〈數書九章〉今譯及研究》，貴州教育出版社，1992，第474 頁。，恐怕有望文生義之嫌。因為《事林廣記》很清楚地記載著宋元之際的“衡”制：

一黍為一絫，十絫為銖，六銖為一分，四分為一兩，十六兩為斤，二斤二兩為裹，十五斤為一秤，三十斤為鈞，四鈞為一石。11陳元靚：《算法類》，中華書局，1999，第202 頁。

與重量相應，還有一種容量。《事林廣記》載：“斛粟數多少之法謂之量，起于粟之一粒?！?2陳元靚：《算法類》，中華書局，1999，第202 頁。量的標準亦以一粒小米的體積為基礎，共分9 個等級。如《孫子算經》云：

量之所起，起于粟。六粟為一圭，十圭為一抄，十抄為一撮，十撮為一勺，十勺為一合，十合為一升，十升為一斗，十斗為一斛。13（唐）李淳風：《孫子算經》，遼寧教育出版社，1998，第1 頁。

關于上述“量”“衡”的內涵，學界已經發表了大量成果，在此不再贅述。這里需要說明的是，在《事林廣記》一書里，不僅記載了社會上通用的度量衡制，還開列了大量藥劑處方，這些處方用藥一般都有專門的量具，有些香藥甚至還要用精美的戥秤來稱量。《事林廣記》載有許多保健處方，藥材的用量都比較少，例如“南陽公主香”組方中載“丁香，麝香，當歸，豆蔻，各一分”14陳元靚：《宮院事宜》，中華書局，1999，第541 頁。。方中“一分”等于“一錢”，文與錢同。這樣的實例亦見于《香譜》與《香乘》兩書，如《香譜》有“麝香一文”的用量，而《香乘》則載“麝香二兩”15（宋）陳敬：《香譜》，江蘇鳳凰文藝出版社，2019，第257 頁。，即可為證。