基于多工作面的鐵路特長隧道施工進度計劃優化
周國華, 張華珂
(西南交通大學 經濟管理學院,四川 成都 610031)
0 引言
鐵路特長隧道指鐵路工程中長10000米以上的隧道,近年來隧道工程逐漸表現出長大、特長的特點。截止2020年底,我國投入運營的特長鐵路隧道209座,總長2811km;在建特長鐵路隧道116座,總長1675km;規劃特長鐵路隧道340座,總長5078km。特長隧道常常是關鍵工程,對于工程按時完工和降低成本意義重大。然而目前特長隧道施工進度計劃大多基于人工經驗編制,輔助坑道的數量和位置等缺少科學高效的決策方法。
隧道工程是施工作業在空間上連續且不斷重復進行的重復性項目[1],傳統CPM等網絡計劃方法在編制這類工程進度計劃時具有諸多缺陷,如破壞了其施工連續性特點[2]、只能用時間維度表達工程進度等[3]。線性計劃方法(Linear Scheduling Method, LSM)由于其能在時間和空間兩個維度上表達工程項目施工進度等優點而被廣泛應用于重復性項目中。如GEORGE[4]研究了基于LSM的資源均衡問題。TANG等[1]在LSM框架下提出了包含多種優化目標的約束規劃模型。
軟邏輯最早由TAMIMI和DIEKMANN[5]提出,相較于固定邏輯而言,軟邏輯指工序在施工單元的執行順序可以變化,而非固定。EL-SERSY[6]指出,通常情況下,帶軟邏輯關系的工序在不同單元上可以同時發生或者交換發生順序。
特長隧道通常開挖輔助坑道來增加工作面實現“長隧短打”,增加工作面則引起工序在不同單元上同時發生,施工方向的改變又使工序發生的順序產生變化,此時隧道邏輯施工順序表現為軟邏輯。軟邏輯關系會引起關鍵路線改變從而縮短工期,但它在具備這種優點的同時增加了問題的復雜性[7],對求解算法也具有更高的要求。FAN等[8]在工序施工隊數量和規模存在多種模式的情況下,構建了基于遺傳算法的軟邏輯調度優化模型。張立輝等[7]針對三類離散時間費用權衡問題,提出了帶有軟邏輯、多模式的項目調度優化模型并采用遺傳算法進行求解。王偉鑫等[9]構建了基于軟邏輯關系的工期-成本多目標調度優化模型,運用通過云模型改進后的遺傳算法求解問題。ZOU和ZHANG[10]考慮了施工隊在不同單元轉移時會產生額外的時間和成本,建立了基于約束規劃的軟邏輯調度模型。已有軟邏輯研究成果的應用對象主要為施工作業空間沒有物理限制的工程,如橋梁工程等,其單元的施工順序既可相互交換,又可并行施工。相較而言,特長隧道作業空間較為封閉,其存在的軟邏輯關系主要是多工作面并行施工,且同一工作面施工單元必須相連,施工順序約束與橋梁工程有很大不同, 如圖1。因此,需要結合隧道工程特點,從新的視角研究具有軟邏輯關系的特長隧道多工作面進度計劃問題。
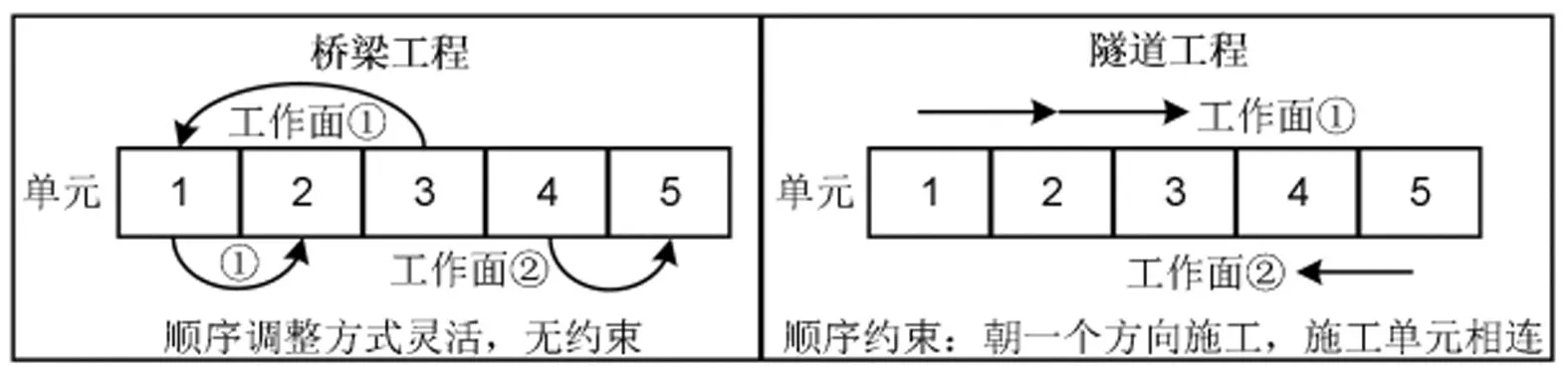
圖1 不同工程施工特點對比
實施多工作面施工時,項目工期縮短使得管理成本等間接成本減少,但同時會引起額外的資源投入導致直接成本增加,進而可能提高項目總成本[11]。如何對工期和成本進行權衡是管理者關注的核心問題。離散時間-費用權衡問題包括三個子問題:(1)工期受限下成本最小化;(2)成本受限下工期最小化;(3)構建時間-費用的Pareto最優解集。本文聚焦于工期受限下成本最小化的問題,以期為施工單位在滿足建設方提出的工期要求下控制施工成本提供一定指導。
基于特長隧道多工作面施工表現出的軟邏輯關系以及項目工期和成本的背反關系,提出工期受限下施工成本最小化的進度計劃優化模型。針對帶有軟邏輯關系的離散時間-權衡問題求解的復雜性以及隧道工程規模龐大的特征,提出改進的遺傳算法對模型進行求解。最后,通過鐵路特長隧道算例驗證模型的有效性和算法的優越性。
1 問題描述及數學模型
1.1 問題描述
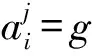
1.2 假設條件
(1)輔助坑道形式為斜井、豎井或橫洞;
(2)可利用輔助坑道單向施工正洞或雙向同時施工正洞;
(3)各班組中每個員工和機械的工效及成本相同[8];
(4)增加工作面引起額外的人工成本和機械成本[8]。
1.3 數學模型
隧道施工進度計劃模型優化目標為最小化隧道施工成本C,由正洞施工人工成本、機械成本、材料成本,輔助坑道成本以及間接成本三部分組成。
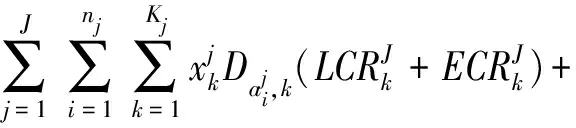
(1)
(2)
(3)
(4)
(5)
(6)
T≤Tmax
(7)
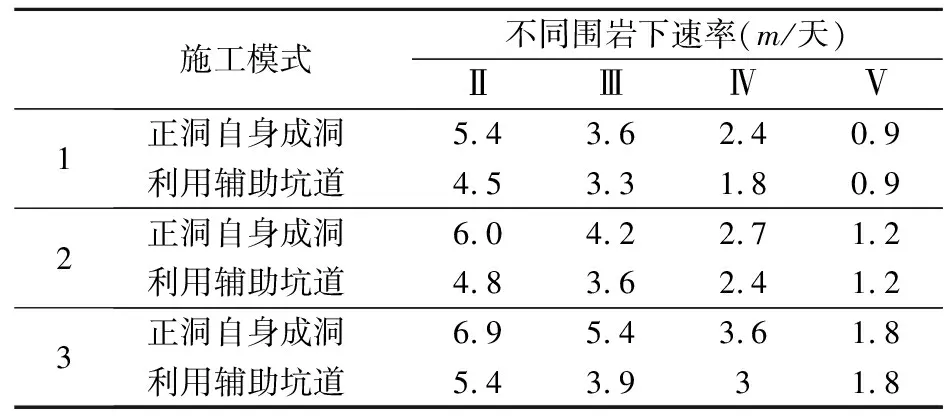
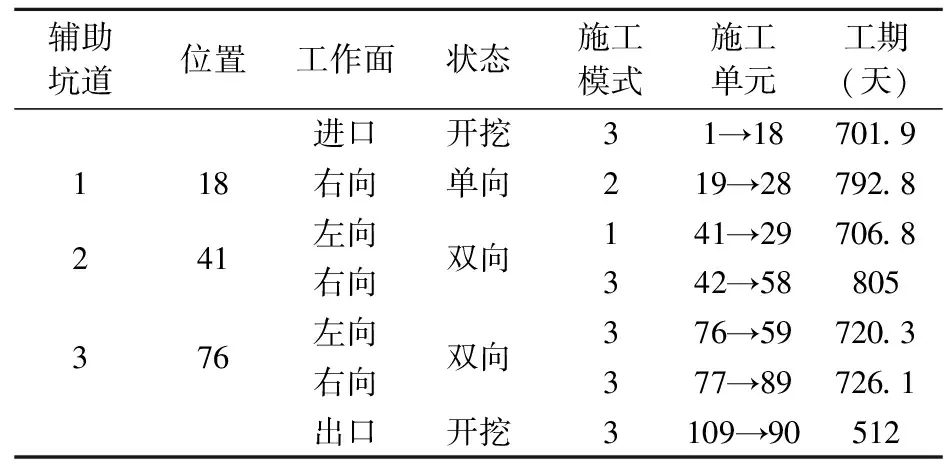
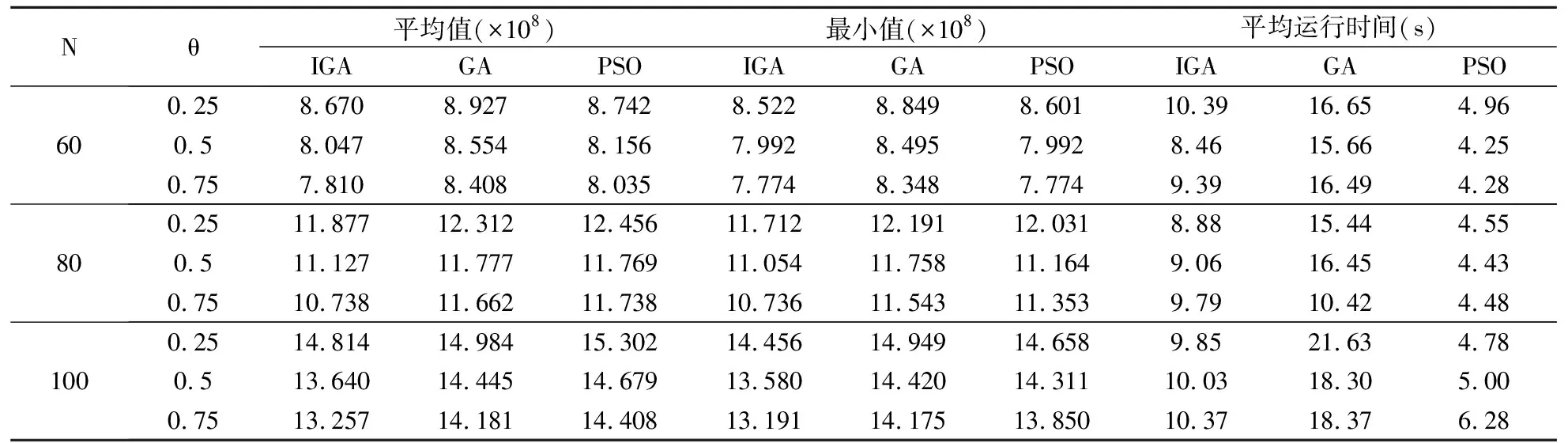
1≤wp (8) yp∈{0,1},p=1,…,2M+1 (9) zj∈{0,1},j=1,…,2M+2 (10) (11) 離散時間-費用權衡問題屬于NP-hard問題[12],精確算法難以對其求解。遺傳算法由于其具有較好的解決NP-hard問題的能力而被廣泛運用于離散時間-費用權衡問題的研究中。本文采用自適應的交叉、變異概率和災變算子以增強遺傳算法的全局搜索能力。同時,為了增強局部搜索能力,將變異算子改進來提高變異后解的質量。 (1)編碼與解碼 圖3 染色體示意圖 (2)初始化種群 每段染色體在各自定義域范圍內隨機生成值,重復Pop次,構成初始種群。其中,Pop為種群規模。由于初始種群的質量對于求解結果影響較大,因此當初始種群所有個體都不滿足截止工期約束時,重新生成初始種群。 (3)適應度函數 在種群中,適應度值越高的個體越優。適應度函數取成本的倒數,對于違反截止工期約束的個體,令其適應度值為足夠小的數。 (4)選擇算子與精英保留 采用輪盤賭選擇算子。同時,為保證算法的收斂性,采用精英保留策略。對于每一代種群,將當代種群中適應度值最高的染色體直接復制進入下一代,替換下一代適應度值最小的染色體。 (5)自適應交叉算子 對于第一段染色體(分段點位置),交叉方式為:隨機選擇交叉點,染色體在交叉點處斷開,父代1分為[Pa1,Pb1],父代2分為[Pa2,Pb2]。保持父代1交叉點前的基因Pa1不變,交叉點后的基因依次選擇父代2中與Pa1不相同的基因,形成子代1;保持Pa2不變,交叉點后的基因依次選擇父代1中與Pa2不相同的基因,形成子代2。對于后三段染色體,分別對每段染色體進行單點交叉。 運用自適應交叉概率。采用變形的sigmiod函數調整概率,使得在遺傳前期交叉概率較大,加強算法的搜索能力,而在后期概率減小,保護優秀個體不被破壞;對于個體而言,讓適應度值更高的個體更容易發生交叉,使優良基因片段更容易傳播,避免早熟現象。遺傳代數為t時第i次交叉的概率見式(12)。 (12) 檢驗生成的子代染色體,如果違反截止工期約束則放棄子代,保留父代。 (6)多重檢驗的變異算子 對每段染色體分別進行基本位變異,特別地,對于第一段染色體,當隨機生成的基因與父代中任一基因相同時,重新生成該基因。采用自適應的變異率,將式(12)中的pc1,pc2分別替換為pm1,pm2(0 為了增強算法的局部搜索能力,對變異后的個體進行檢驗。第一,判斷子代個體是否滿足截止工期約束;第二,判斷子代個體適應度值是否大于父代種群中的最差值。任何一個條件不滿足則放棄子代,保留父代。 (7)改進的災變算子 為了增強算法的全局搜索能力,引入災變算子。對災變方式進行改進。災變條件和災變方式設計如下:1)災變條件:當連續Ca代種群中最高適應度值相同時,發生災變;2)災變方式:在原有種群中隨機選擇比例為pz的個體,其余1-pz個體重新生成。將種群中適應度最差的個體替換為保留的精英個體,形成新種群。 (8)算法終止條件 當算法迭代次數達到Mt終止算法,輸出最優值和最優解。 Step1輸入工程進度和成本相關參數,輸入遺傳算法參數,種群規模Pop、最大迭代次數Mt,交叉概率pc1,pc2,變異概率pm1,pm2,災變參數Ca,pz。 Step2生成初始種群。令進化代數t=1。 Step3計算適應度值并執行精英保留。 Step4執行輪盤賭選擇操作。執行交叉操作,隨機選擇兩條染色體,判斷是否進行交叉,循環Pop/2次。執行變異操作,隨機選擇一條染色體,判斷是否執行變異操作,循環Pop次。 Step5判斷是否執行災變算子,若是則對Step4中生成的種群進行災變;否則跳過該步驟。令t=t+1。 Step6判斷:若t>Mt,轉Step7;t≤Mt,轉Step3。 Step7進化完成,輸出第Mt代的最優值及相應最優解。 以鐵路特長隧道工程數據為算例。算法編程在MATLAB R2018b上實現。 鐵路特長隧道全長18226米,為了滿足工期要求,采用開挖輔助坑道、增加工作面的方式來縮短工期。增加的工作面的數量、施工范圍和方向的改變會引起隧道邏輯施工順序的變化,該特長隧道施工順序從而表現為軟邏輯。以該鐵路特長隧道工程數據對模型和算法的有效性進行驗證。 將該特長隧道按圍巖級別劃分施工單元,單元長度超過300米時,以300米為界進行細分,單元工作量和圍巖情況見表1。不同施工模式下正洞進度指標見表2,正洞自身成洞指從隧道進、出口開挖,不利用輔助坑道,其與利用輔助坑道開挖的速率不同。備選輔助坑道數量為5,不同工作面數量下不同模式對應的成本信息見表3。不同位置處輔助坑道施工時間及成本見表4。工程間接成本率ICR為20000元/天。截止工期Tmax為810天。 表2 正洞施工進度指標 表4 輔助坑道備選位置施工時間及成本 運用提出的改進遺傳算法求解,設置算法參數如下:種群規模Pop為100,自適應交叉概率pc1為0.9,pc2為0.5,自適應變異概率pm1為0.1,pm2為0.001,災變參數Ca為10,pz為0.1。經過多次試驗設置最大進化次數Mt為1000代,以在保證解的有效性的同時算法具有較高的運行效率。進度計劃輸出結果見表5。 表5 進度計劃輸出結果 求解結果表明:共需開挖3個輔助坑道,設置7個工作面,總工期為805天。總成本為1.65×109元,其中,正洞施工人工成本2.98×108元,機械成本3.98×108元,材料成本9.16×108元,輔助坑道開挖成本1.75×107元,間接成本1.61×107元。 運用提出的算法得出了滿足截止工期前提下,施工成本最小化的特長隧道施工進度計劃以及成本構成信息,模型和算法的有效性得以驗證。 為測試本文算法,保持其它參數不變,設計規模和截止工期不同的算例。單元規模N包括60,80,100,單元從表1中隨機抽取并隨機排列。截止工期的設置方式如下:首先計算出無輔助坑道進、出口工作面以最小速率施工時的最長工期LT,再計算所有工作面同時以最大速率施工時的最短工期UT,最后設置截止工期Tmax=UT+(LT-UT)θ,其中,θ表示截止工期的松弛度,θ∈{0.25,0.5,0.75}。 對于每個算例,將提出的改進遺傳算法(IGA)、標準遺傳算法(GA)和粒子群算法(PSO)各運行20次,仿真結果見表6。取θ=0.5時三種規模下各算法的運行結果進行比較,見圖4。GA中交叉概率設置為0.9,變異概率為0.1;PSO中慣性權重為0.8,個體學習因子和群體學習因子均為2,最大速度為1,其余參數和輸入數據與3.2中一致。運算環境為操作系統為Windows 10,處理器為Intel Core i7-8565U,CPU主頻1.99GHZ,內存為8GB的個人電腦。 表6 算法仿真結果 由表6可以看出,三種算法分別運行20次,IGA得到的平均值和最小值均較GA和PSO更小,證明IGA具有更強的尋優能力。另外,由圖4可知,隨著問題規模增大,GA和PSO在求解時極易陷入局部最優,且PSO得出的解的波動性較大,而IGA求得的解更小且更加穩定。在運行速度上,IGA較于傳統的GA更快,這是由于IGA優化了GA的搜索機制,提高了運行效率。IGA的速度不及PSO是因為PSO無需進行遺傳算法中的交叉變異等運算。以上結果說明所提的IGA對于大規模隧道進度計劃優化問題具有較好的尋優能力和較快的運行速度。 針對多工作面的特長隧道進度計劃優化問題,構建了工期受限下施工成本最小化的軟邏輯進度計劃優化模型,設計了自適應的交叉和變異概率、多重檢驗的變異算子和改進的災變算子對算法進行優化,并基于不同算例開展了實驗研究。結果表明:(1)提出的軟邏輯施工進度計劃優化模型和算法能夠有效地應用于特長隧道工程,優化后的進度計劃能夠為施工單位實際施工提供一定參考。(2)改進后的遺傳算法相較于標準遺傳算法和粒子群算法具有更強的全局尋優能力,在運行速度上比標準遺傳算法更快,在求解大規模特長隧道進度計劃優化問題上表現出更好的性能。 本研究適用于輔助坑道為斜井、豎井或橫洞的情形,當輔助坑道為平導加橫通道時,需要根據平導超前開挖情況調整施工順序,將通過進一步研究對其完善。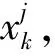
2 算法設計
2.1 算法基本要素


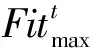
2.2 算法求解步驟
3 算例分析
3.1 算例描述

3.2 求解結果
3.3 算法對比
4 結論

