基于演化博弈的生產作業現場工人安全紐帶締結的驅動機制研究

吳春林, 楊 洋, 翟峰羽, 趙墨非

(1.北京航空航天大學 經濟管理學院,北京 100191; 2.東北財經大學 投資工程管理學院,遼寧 大連 116023)

0 引言

安全是人類最基本的需求,社會經濟發展和追求美好生活必須以安全為前提。習近平總書記強調,人命關天,發展絕不能以犧牲人的生命為代價。目前,我國安全生產形勢依然嚴峻復雜, 2020年全國生產安全事故3.8萬余起,死亡人數高達2.74萬余人[1]。作為最危險的行業之一,建筑業每年都有近4000人死于施工現場[1]。受個體先天差異、崗位角色差異、組織環境差異等影響,工人不安全行為在現場具有極為多樣、動態且復雜的表現,一直是事故防控體系最薄弱的環節[2],對于科學研究還是安全管理實踐都是根本性難題。

傳統上,改進作業現場工人安全狀況的最直接思路是加強管理,通過制定嚴格的規章制度,禁止工人的不安全行為[3-6]。這一思路屬于“自上而下”,通過法規約束,實現“要工人安全”;但很顯然,對工人的約束規則制定不同于對自動機器(Automata)的規則設定,工人會自主進行決策,決定是否遵守法規約束,是完全遵守還是打折扣地遵守,因此,考慮工人的決策偏好,激發工人產生“我要安全”的主觀意愿尤為重要。事實上,近年來一批文獻發現:與硬性安全規章相比,工人對同一作業小組內班組長、工友等相似層級人員的安全提醒、指導和溝通有更高的接受度[7],當工人面臨安全問題或身處險境時,可以倚賴同組工友保護自己免受傷害。TR?STER等[8]研究將工人間的個體紐帶引入考慮,假設作業現場人員之間存在兩種紐帶關系,工作型紐帶單純是以工作為目的而產生的信息傳遞和人際互動,不依賴于雙方的情感和友誼基礎,可以為單向關系,也可以為雙向關系;而友誼型紐帶可以為個體提供社會和情感支持,其形成依賴于雙方的互惠和積極反饋,必須為雙向關系。根據社會交換理論,在接受他人幫助后,工人也會主動幫助他人,如向工友傳遞有價值的安全信息、傳授安全知識與技能、提醒身處險境的工友注意安全等,這些無形的安全紐帶實現了人員的互幫互惠,從而及時、全面地控制現場安全隱患,防范安全事故[7]。本文即從工人自主結成安全紐帶的策略性問題出發,研究其對作業安全的影響。

本文采用演化博弈方法刻畫作業現場工人的動態安全交互關系。工人個體具備有限理性,根據自身需求和未來損益預期而調整行為策略、追求個體利益改善、并依據過去與工友的多次交互博弈的結果,來緩慢調整自身是否發起安全交互的決策傾向性和概率,直至紐帶穩定,這些特征較好地對作業現場工人的決策環境進行了概括[9-12]。尤其值得注意的是,工人間締結友誼型紐帶對工人的收益具有超模性[13],即友誼型紐帶的締結會導致工人雙方收益的增多,且增多的額外收益具有不確定性,該種額外收益能在模型中發揮“引力點”的作用,吸引并驅動工人雙方通過發起安全交互而締結友誼型紐帶以獲得更多的收益,進一步地,影響工人雙方最終作出的決策。

此外,生產安全不同于其他管理學問題。在演化博弈過程中,安全紐帶的締結通常依賴于反復嘗試過程中的損益的激勵和引導。然而“安全無小事”,每一次損益的實現都可能帶來財產乃至生命的代價。因此,對締結安全紐帶的演化博弈系統而言,重要的不僅是演化結果,還有演化速率。本文從微觀視角尋找驅動系統加速演化至理想狀態的關鍵因素,使系統在短時間內到達穩定點。

綜上所述,本文運用演化博弈方法分析作業現場工人間安全紐帶的締結機理及促使該過程快速進行的方法,以促使工人“要我安全”向“我要安全”的意愿轉變,解決作業現場工人不安全行為的治理問題。

1 作業現場工人安全交互演化博弈模型構建

本文考察任意一對作業現場工人,并對雙方的策略和收益進行如下假設和說明:

(1)工人間安全行為的發起的博弈中,將博弈雙方工人分別記為工人A和工人B。工人有兩種策略,即可以選擇發起安全交互(I)或不發起安全交互(NI)。雙方基于有限理性,在博弈過程中不斷學習進而調整策略,直至形成穩定策略。

(2)若工人A和工人B不與彼此發生安全交互,在對方有困難(陷入安全險境、遭受安全隱患)時也不提供任何幫助,則雙方不締結任何安全紐帶,雙方的安全意識和安全知識也不會得到有效提升,記雙方此時收益為0。

(3)當工人單方發起安全交互,如:工人A主動向工人B發起安全交互,工作型紐帶便會締結。工人A的利他行為有一定概率(P1)被領導識別,并獲得獎勵R1(R1≥0),受協助的工人B以提升自身安全意識和安全知識,獲得收益R2(不論是否被領導識別)。此外,對于博弈雙方均發起安全交互,設置參數Q(Q≤1),用以區分在博弈中因雙方發起先后或發起情況不同導致R1不同(例如,當A先發起,可設置Q1=0.9,Q2=0.8;當只有一方發起時Q=1)。

(4)由于雙方的主觀性格因素(SPF)、雙方對組織的歸屬感(SOB)等的差異,使得友誼型紐帶無法在每一次共同發起安全交互時都能形成,因此假設友誼型紐帶締結的概率為P3。

(5)工人主動與別人發生安全交互需消耗成本,如時間成本、精力成本以及潛在的事故風險,假設該成本為C。根據以上假設,在不同策略組合條件下,工人收益矩陣如表1所示。

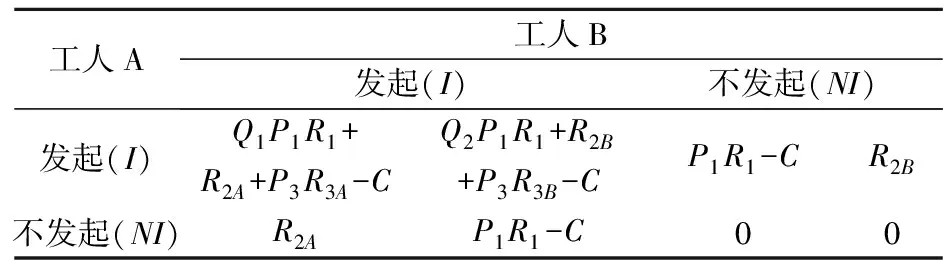
表1 演化博弈支付矩陣

2 演化博弈分析

2.1 復制動態方程與系統演化平衡點的求解

假設作業現場工人A采取發起(I)策略的比例記為x(0≤x≤1),則采取不發起(NI)比例的概率為1-x;同時,假設作業現場工人B采取發起(I)策略的比例為y(0≤y≤1),采取不發起(NI)策略的比例為1-y。

根據表1所示的博弈支付矩陣,當工人A選擇發起(I)策略時,其獲得的期望收益為:

U1A=y(Q1P1R1+R2A+P3R3A-C)+(1-y)(P1R1-C)

(1)

當工人A選擇不發起(NI)策略時,其獲得的期望收益為:

U2A=yR2A

(2)

因此,工人A在上述兩個策略條件下的綜合期望收益為:

(3)

同理,可以得到工人B采取發起(I)策略時的期望收益為:

U1B=x(Q2P1R1+R2B+P3R3B-C)+

(1-x)(P1R1-C)

(4)

工人B采取不發起(NI)策略的期望收益為:

U2B=xR2B

(5)

綜上,工人B在上述兩個策略條件下的綜合期望收益為:

(6)

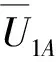
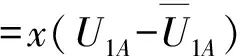
=x(1-x)[y(Q1P1R1+P1R3A-

P1R1)+P1R1-C]

(7)

同理,設M(y)表示工人B采取發起(I)策略的概率的變化率,工人B采取發起(I)策略的復制動態方程為:

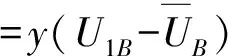
=y(1-y)[x(Q2P1R1+P3R3B-

P1R1)+P1R1-C]

(8)

工人A和工人B的安全交互可由微分方程構成的二維動態系統描述,具體如式(9)所示:

(9)

由微分方程穩定性理論[15]可知,復制動態方程穩定點是其零點處一階導數小于0的點,即需滿足:

{dF(x)/dx≤0|F(x)=0,x∈[0,1]}

(10)

因此,令F(x)=0,可解得x=0,x=1或x0=(P1R1-C)/[(1-Q2)P1R1-P3R3B] ;同理,令M(y)=0,可解得y=0,y=1或y0=(P1R1-C)/[(1-Q1)P1R1-P3R3A] ,因此,系統的平衡點為E1(0,0),E2(0,1),E3(1,0),E4(1,1),E5(x0,y0)。且當(1-Q2)P1R1-P3R3BP1R1-C>0且(1-Q1)P1R1-P3R3A>P1R1-C>0成立時,E5滿足演化平衡點的要求。

2.2 演化平衡點穩定性分析

根據FRIEDMAN[9]提出的方法,對于由微分方程系統描述的動態博弈過程,平衡點的穩定性和演化穩定點,可由該動力系統的雅可比矩陣的局部穩定性分析得出。為了分析在不同參數條件下平衡點的穩定情況,設置三個條件。條件一:P1R1-C<0;條件二:Q1P1R1+P3R3A-C<0;條件三:Q1P1R1+P3R3B-C<0。三個條件的滿足與否,會產生8種不同情景,且每種情景對應一種可能成立的穩定點組合。可根據雅克比矩陣的穩定性來驗證這些點組合是否為雙方最終達成的演化穩定策略。對x′,y′分別關于x,y求偏導數,相應的雅可比矩陣為:

(11)

記行列式為detJ,矩陣的跡為trJ,由FREIDMAN提出的方法可知:只有當detJ>0,trJ<0時,策略為演化穩定策略[9]。將4個平衡點代入雅克比矩陣,如表2所示。

表2 系統演化穩定性表征

由表2可進一步得到博弈雙方不同條件下的平衡點組合,歸納于命題1中。

命題1系統均衡收斂的情形如下:

a.如果P1R1-C<0,Q1P1R1+P3R3A-C<0且Q1P1R1+P3R3B-C<0,僅有平衡點(0,0)。

b.如果P1R1-C<0,Q1P1R1+P3R3A-C<0且Q1P1R1+P3R3B-C>0,僅有平衡點(0,0)。

c.如果P1R1-C<0,Q1P1R1+P3R3A-C>0且Q1P1R1+P3R3B-C<0,僅有平衡點(0,0)。

d.如果P1R1-C<0,Q1P1R1+R3R3A-C>0且,Q1P1R1+P3R3B-C>0,系統有平衡點(0,0)與(1,1)。

e.如果P1R1-C>0,Q1P1R1+P3R3A-C<0且Q1P1R1-C<0,系統有平衡點(0,1)與(1,0)。

f.如果P1R1-C>0,Q1P1R1+P3R3A-C<0且Q1P1R1+P3R3B-C>0,僅有平衡點(0,1)。

g.如果P1R1-C>0,Q1P1R1+P3R3A-C>0且Q1P1R1+P3R3B-C<0,僅有平衡點(1,0)。

h.如果P1R1-C>0,Q1P1R1+P3R3A-C>0且Q1P1R1+P3R3B-C>0,僅有平衡點(1,1)。

以子命題a為例,當條件一、二、三均滿足,即P1R1-C<0,Q1P1R1+P3R3A-C<0且Q1P1R1+P3R3B-C<0,將該三式帶入表2中可計算得到(P1R1-C)2>0,且2(P1R1-C)<0,由FRIEDMAN[9]提出的判定定理可知,該條件下(0,0)點對應的行列式的值detJ>0且跡trJ<0,可判定(0,0)點為穩定點。對于(0,1)點,Q1P1R1+P3R3A-C<0且P1R1-C<0,故對應的行列式detJ=(Q1P1R1+P3R3A-C)×(C-P1R1)<0,因此(0,1)點為不穩定點。同理,Q1P1R1+P3R3B-C<0且P1R1-C<0,故(1,0)點所對應的行列式的值小于0,因此(1,0)點也不是穩定點。對于(1,1)點,由于Q1P1R1+P3R3A-C<0且Q1P1R1+P3R3B-C<0,其對應的跡小于0,因此(1,1)點也不是穩定點。同理,對于子命題b至g,將條件帶入表2中,計算方法如上述過程,則命題可得到證明。

由于本文主要討論工人的決策如何快速向雙方同時發起安全策略演化(即如何快速演化至(1,1)),可發現命題1的子命題d與h中,(1,1)點均為穩定點,即博弈雙方均可能演化至該點。其中h中,由于僅存在(1,1)為穩定點,因此整個系統經過一段時間的演化后,只會在(1,1)點達到穩定。對于情況d,(0,0)也是穩定點,工人的決策將會在(發起,發起)與(不發起,不發起)間演化。接下來,本文即針對d情形進行演化博弈穩定性分析。

2.3 博弈雙方策略穩定性分析

當時間t不斷增大時,系統中,博弈雙方的策略會在多次博弈后演化至穩定。對于一個由微分方程組成的動態系統,當F′(x)<0時,且x本身是穩定狀態的平衡點時,則x為博弈一方的穩定策略。根據Friedman提出的方法,可用雅克比矩陣的局部穩定性來驗證雙方所形成的策略組合是否為演化穩定策略(ESS),并分析影響策略選擇的因素。

對于工人A:

對F(x)關于x求導,得:

F′(x)=(1-2x)[y(Q1P1R1+P3R3A-

P1R1)+P1R1-C]

(12)

當F′(x)<0時,記:

y0=(P1R1-C)/[(1-Q1)P1R1-P3R3A]

(13)

命題2當滿足命題1中d情形時:

(1)當工作滿意度期望值P3R3A<(1-Q1)P1R1時,工人雙方會選擇“不發起”策略。

(2)當工作滿意度期望值P3R3A>(1-Q1)P1R1時,工人雙方會選擇“不發起”或“發起”策略。

(3)當工作滿意度的期望值P3R3A<(1-Q1)P1R1時,因P1R1-C<0,安全投資總額固定且作業現場工人因博弈雙方均發起安全交互使得工人獲得的領導者的青睞和獎勵減少的收益差額部分與締結友誼型紐帶所獲得的收益的大小關系確定,可計算得對于?x∈[0,1],由于存在F′(0)<0,F′(1)>0,說明此時x=0時穩定決策,即工人雙方會選擇“不發起”策略。

當工作滿意度的期望值P3R3A>(1-Q1)P1R1時,因P1R1-C<0且Q1P1R1+P3R3A-C<0,可知對于任意一個x均有y屬于一個開集,使得F′(0)<0,F′(1)>0或F′(0)>0,F′(1)<0,且臨界值y=y0。說明對于不同初值的(x,y),在系統經演化后博弈雙方可能會同時選擇“發起”或同時選擇“不發起”策略。

2.4 作業現場工人雙方演化博弈結果的比較靜態分析

為具體分析影響雙方是否發起安全行為的因素,選擇研究演化穩定點為(1,1),(0,0)時的情景,即滿足命題1中子命題d的條件。

依據雅可比矩陣的穩定性分析,(1,1),(0,0)為演化穩定點組合,(1,0),(0,1)為不穩定點組合。對于點((P1R1-C)/((1-Q2)P1R1-P3R3B),(P1R1-C)/((1-Q1)P1R1-P3R3A)),其雅可比矩陣detJ<0,而trJ=0,則記其為鞍點。

對于(x0,y0)未知的情況,建立ABCM面積S1和區域面積S2的函數計算式,四邊形面積即代表工人演化至某均衡點的概率,因而四邊形面積表達式的參數為系統演化穩定策略的影響因素,若S2>S1,系統將朝著理想點D(1,1)演化的概率更大。即當初始條件確定時,當任意落在S2中的點(x0,y0)都會向(1,1)演化,可知初始狀態在M點附近時,細微變化都會影響最終演化結果。根據演化相位圖中信息可求得:

(14)

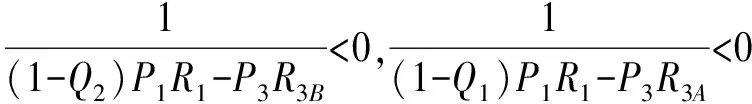
當其他參數不發生變化時,求S2關于C的導數,得到:

(15)

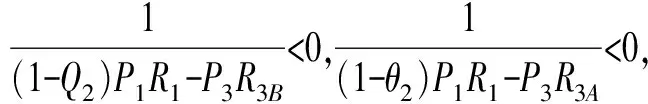
所以該偏導數的值小于0,即當其他參數保持不變的情況下,隨著參數C的增加,四邊形的面積S2會逐漸減小,博弈雙方向(不發起,不發起)演化的概率增大。這說明隨著工人發起安全行為的成本的增加,工人更可能會趨向于不發起安全行為。

對于其他因素,如P1,R1,Q1,Q2,P3等分析方法相同,所得結論匯總如表3所示。

表3 雙方博弈影響因素的分析結果

3 演化速率分析

演化博弈,即博弈雙方基于以往經驗選擇相應策略。本文用t表示該系統在處于特定環境下從演化過程開始至雙方演化至穩定點的整個過程所經歷的時間。顯然,對于同樣的系統環境,若經驗積累的過程越快,則演化的速率越高。而對于不同的系統環境,本文從微觀視角研究演化時間t,有助于尋找加速系統演化至理想狀態的關鍵因素,從而使系統在短時間內到達穩定狀態。

為探究系統環境參數與期望時間t的關系,聯立發起安全交互概率的微分方程表達式:

(16)

可通過求解該非齊次非線性微分方程組得到x與y關于時間t的表達式。對于工人A發起安全交互的比例x,設求解后表達式為x=W(t)+μ1。當t0=0時,系統處于初始未演化狀態。當演化完成,工人選擇發起安全交互比例x與y為1或0,即當t>t1,對于任意x和t都有x′=0,即x′=x″=0。因此,工人A發起安全交互的演化時間為系統演化完成的時刻減去系統開始演化的時刻,即t-t0,又因為t0=0,所以工人A發起安全交互的演化時間為t1。同理,工人B發起安全交互比例為y=G(t)+μ1,演化時間為t2。則整個系統的演化時間為t1與t2的較大值。由t1與t2分別對應的是W′(t)=W″(t)=0、G′(t)=G″(t)=0的解,且表達式含環境變量C,R1,Q1等,演化時間與環境變量的取值有關。

對于方程組的求解,由于其為一般非齊次非線性微分方程組,并無顯示解,因此本文通過設定特定情景,利用Matlab 2018b軟件對模型進行數值仿真,并進行分析。

4 演化博弈模型的仿真分析

為了定量分析各因素對系統最終演化結果以及演化速率的影響,本文使用Matlab 2018b軟件對該系統進行了仿真分析。此時,博弈系統的最終穩定狀態取決于博弈模型中的參數值以及雙方初始發起安全交互的比例(x,y)。本文選用ode45指令求解復制動態方程、以及模擬系統的演化過程,討論系統中參數對演化結果與速率的影響。各參數的初始值設定如表4所示,通過設定一定的系統參數初值,可得到系統演化趨勢圖如圖1(a)-圖1(d)所示。

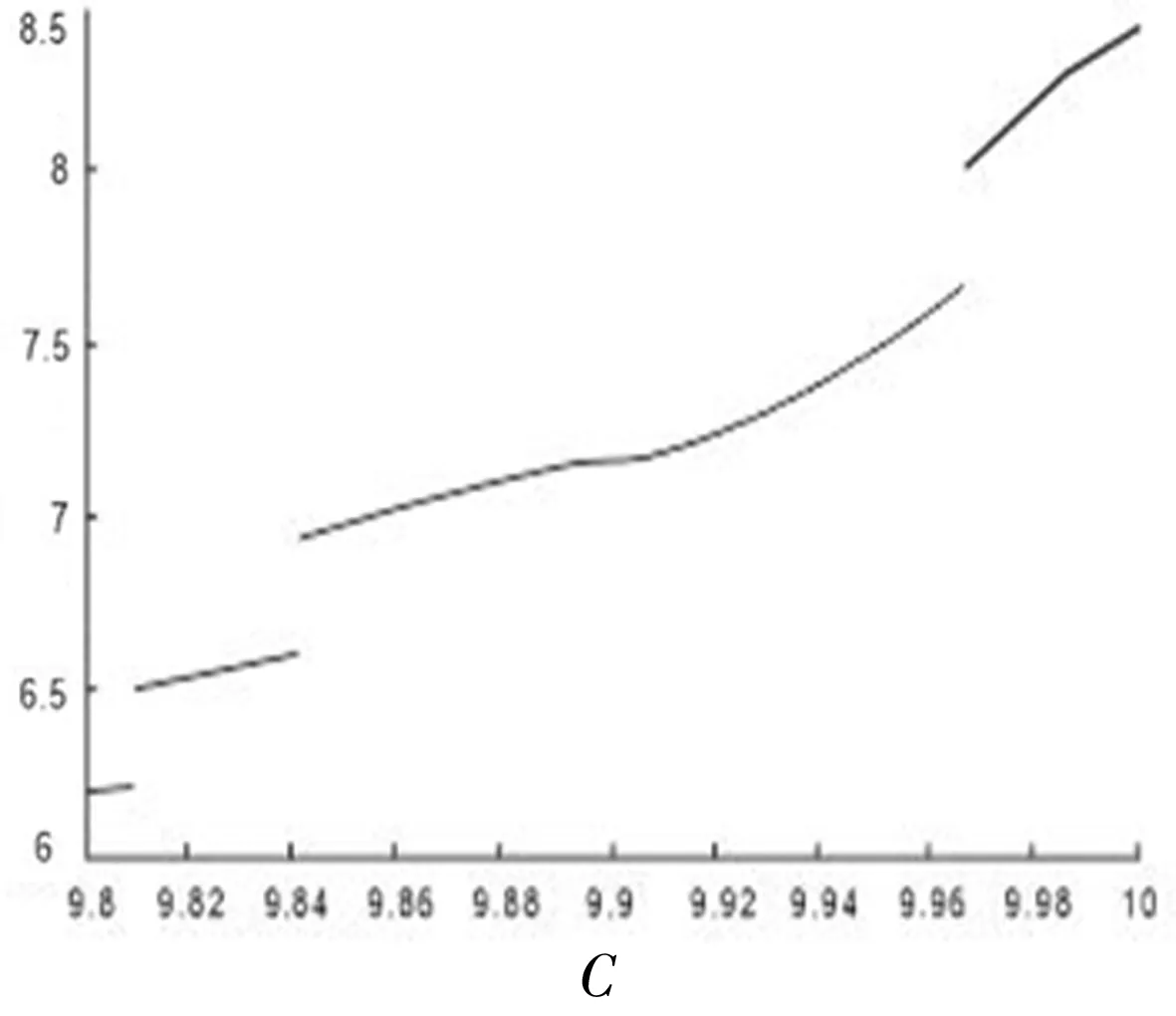
(a)發生安全交互的成本(C)的影響

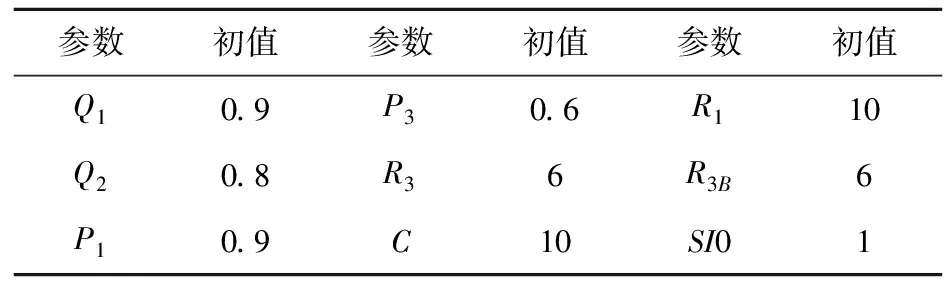
表4 參數初始化數值表

4.1 工人發起安全交互的初始比例

工人發起安全交互的初始比例是本文系統中的一個重要參數,它影響著工人是否選擇發起安全交互。設置三組不同的(x,y)的初值(如表5所示),得到系統演化過程的仿真結果。結果表明了在給定參數不變的情況下,當工人發起安全交互的初始比例均等于0.5時,博弈雙方的策略均最終演化至發起安全交互。由情況1、情況2與情況3相互對比可發現,若某一方工人發起安全交互的比例較低(如情況2與情況3),則博弈系統需經過更長的一段時間才能演化至博弈雙方均選擇發起安全交互,或演化至博弈雙方均不發起安全交互。在此情況下,由于演化從起點至終點的位移發生變化,固探究期望時間t失去意義,因此本文僅探究環境參數對于期望時間的影響。

表5 三組不同(x,y)的初值

4.2 博弈系統環境參數

工人發起安全交互的成本、工人發起安全交互后得到的期望獎勵、締結安全紐帶的期望收益以及收益系數均是決定工人的收益情況的關鍵因素,因此影響著工人發起安全交互的比例以及系統演化的速率。根據表五初值進行仿真實驗的結果說明:降低工人發起安全交互的成本或提高工人發起安全交互后得到的期望獎勵、締結安全紐帶的期望收益以及收益系數能促使工人的決策向發起安全交互演化,并能縮短工人雙方均發起安全交互的系統的演化時間。

5 結論與建議

本文構建了作業現場工人安全紐帶締結演化博弈模型,分析了作業現場工人之間安全交互策略選擇動態變化過程,發現單方發起安全交互獲得的組織獎勵小于發起成本,或工人雙方均發起安全交互情況下獲得的組織獎勵小于締結友誼型安全紐帶得到的收益時,博弈雙方最終演化穩定策略為(1,1),(0,0)。作業工人策略選擇以及工人發起安全交互概率最終沿哪條路徑演化與博弈初始狀態以及博弈支付矩陣的參數密切相關。系統演化的速率與工人發起安全交互的次數正相關,且受系統環境參數初值影響。基于以上分析結論,并結合生產安全事故高發的行業工人的特點,提出如下管理建議:

(1)構建核心作業團隊。為減少工人不安全行為,使工人主動發起安全交互,鼓勵企業培育并建立自有核心作業工人隊伍,提升工人專業技能與安全知識。并制定安全交互獎勵機制,對樂于進行利他互動的工人予以專項獎勵。

(2)完善職業技能培訓體系。強化企業技能培訓主體作用,推行終身職業技能培訓制度,可統一在培育基地培訓,增強組織凝聚力、歸屬感,提高工人們的風險感知能力,從而促進工人從情感上更愿意發起安全交互行為。

(3)健全保障薪酬支付的長效機制。聘用工人時須簽訂勞動合同,未訂立勞動合同并實名登記的工人不得進入現場作業,推動按項目參加工傷保險,結合實名制管理,確保工傷保險覆蓋作業現場所有工人,讓工人感受到政府或企業對自己人身的關懷。

(4)關注并調動工人發起安全交互的主觀能動性。設計用于測試工人主動發起安全交互意愿的問卷,于招聘工人時用作參考,選取更主動發起安全交互的工人,以減少不安全行為,減少安全事故的發生。同時,在作業期間定期開展工人安全交互主觀能動性測驗并對測驗成績優秀者給予一定獎勵,以調動工人發起安全交互主觀能動性。