基于遺傳算法的裝配線平衡與物料超市規劃協同優化

彭運芳, 孫魯蒙, 彭雪芬, 夏蓓鑫

(上海大學 管理學院,上海 200444)

0 引言

近年來,越來越多的制造企業開始使用線邊物料超市來代替傳統的中央倉庫以保證裝配線上零件的準時化供應。裝配線平衡和物料超市規劃是裝配系統設計的兩個重要決策,企業通常在裝配線平衡階段獲得最優工作站的數量,再進行物料超市的布置,這種尋優過程可能會造成超市數量或搬運成本的增加。裝配線平衡和物料超市規劃協同優化是站在整體的角度更系統地進行生產線規劃,有效地提高裝配線系統的速度和柔性,減少投資風險,增強企業競爭力。

裝配線平衡問題(Assembly Line Balancing Problem,ALBP)需要在滿足有限資源約束的情況下將裝配工序有效地分配到各個工作站,多采用啟發式算法求解,如遺傳算法[1]、蟻群算法[2]、粒子群算法[3]、以及集數搜索算法[4]等。BATTINI等[5]運用分步程序來確定何時何處建設物料超市。EMDE[6]提出了一個數學模型來確定超市最佳數量和布局。ALNAHHAL和NOCHE[7]使用整數規劃模型和實數遺傳算法來求解超市的數量和位置,以減少運輸和庫存系統的固定成本。ZHOU和TAN[8]以運營成本和運輸成本最小為目標建立數學模型,提出了一種具有差分進化策略的分布自適應估計算法研究超市選址問題。針對兩者結合的問題,BATTINI[9]提出作為零件供應中的長期決策問題的超市規劃問題應與ALBP一起考慮。針對兩者結合的問題,NOURMOHAMMADI和ESKANDARI[10]提出了分階段的數學模型,NOURMOHAMMADI等[11]提出了綜合模型,但綜合模型并未考慮超市的分配問題以及運輸成本。2019年他們增加了對工序時間和需求的不確定的考慮,但仍然通過分階段法進行求解[12]。2020年FATHI等[13]利用模擬退火算法對裝配線平衡和超市選址問題進行求解。

綜合以上研究可以發現,目前對于裝配線平衡和超市規劃的問題仍以分階段方法為主,協同優化依然是一個新鮮領域。本文從裝配線規劃的整體角度出發,建立以最小化工作站及物料超市的建設成本和加權運輸成本為目標的混合整數規劃模型,設計了一種新的編碼方式對遺傳算法進行改進,以求解大規模問題。

1 問題描述

裝配線平衡問題(ALBP)就是將具有優先次序的一系列裝配工序合理地分配到各個工作站上,是生產線設計階段的核心決策[14]。各個工序之間的優先關系,一般用優先關系圖來表示,圖1為經典的Bowman平衡問題,圓圈代表工序,圓圈內的數字是工序序號,箭頭表示工序間的優先關系,圓圈上方的數字表示工序j的加工時間tj,圓圈下方的數字表示工序j的零件料箱需求量dj。

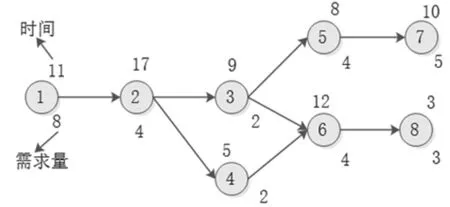
圖1 優先關系圖示例

圖2顯示了一個帶有2個物料超市,10個工作站的直線型裝配線布局圖。物料超市位于其底部,裝配線上所需要的零部件都按照標準尺寸裝箱,貯存在物料超市里。每個工作站只能由一個超市供應物料,每個超市只能供應一段連續的工作站。每個超市s都有容量限制Caps,每個超市所負責的一段工作站(從工作站k至工作站l)的物料需求量demkl不能超過其容量限制。牽引小車從超市出發,將料箱送至對應的工作站,再返回至超市結束一次行程。牽引小車一次運送的路程distskl計算式如下:

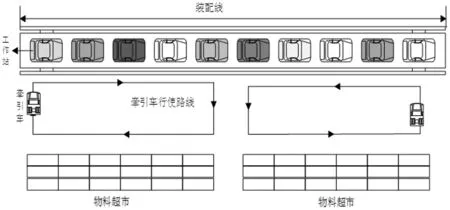
圖2 裝配線布局圖

distskl=|xs-xk|+|xs-xl|+|xk-xl|+

|ys-yk|+|ys-yl|+|yk-yl|

(1)

其中,xs,ys,xk,yk,xl,yl分別為超市s、超市負責的第一個工作站k和最后一個工作站l的橫縱坐標,超市s到任意工作站k的路程bsk為:

bsk=|xs-xk|+|ys-yk|

(2)

圖3和圖4針對上述簡單例子給出了分階段法和協同優化法下的結果。其中生產節拍設定為20,每個超市容量為20,超市和工作站的建設成本均為300,單位距離成本為1,各工作站和超市橫坐標分別為0,3,6,9,12,和0,9,縱坐標分別為5和0。分階段法中先在生產節拍的約束下最小化工作站數量。小車從物料超市滿載出發,每到達一個工作站而后卸下一部分物料,權重也隨之改變,最后完成全部運送任務后空載返回。因此上述過程中總成本分為超市建設成本、工作站建設成本和運輸成本。分階段法的總成本計算過程如下:2×300+5×300+5×16+3×8+3×4+11+16×5+3×9+8=2342。而協同優化中,得出總成本為2330,比分階段成本低,說明協同優化能夠有效降低總成本。

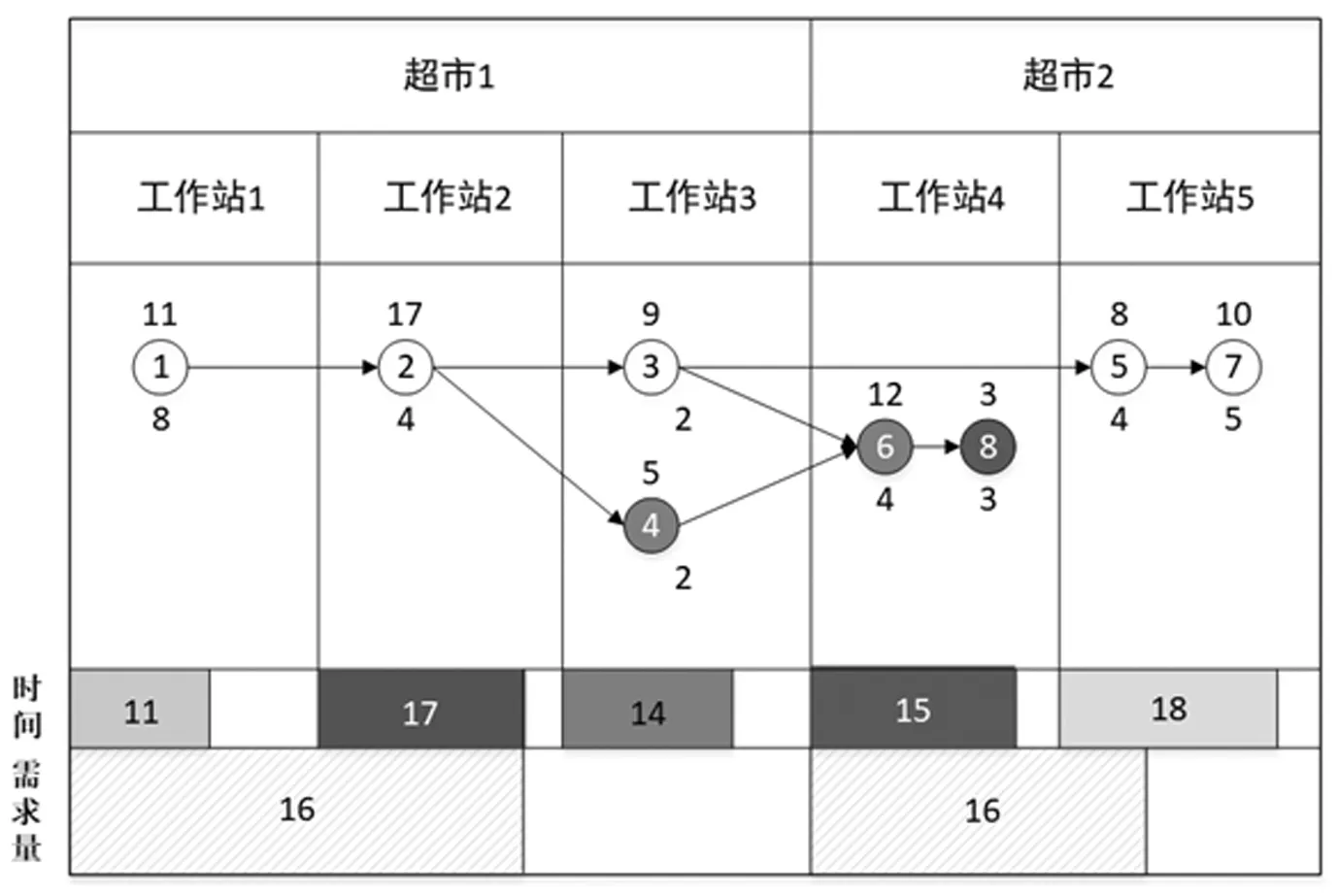
圖3 分階段法優化的最優裝配線平衡與物料超市規劃方案

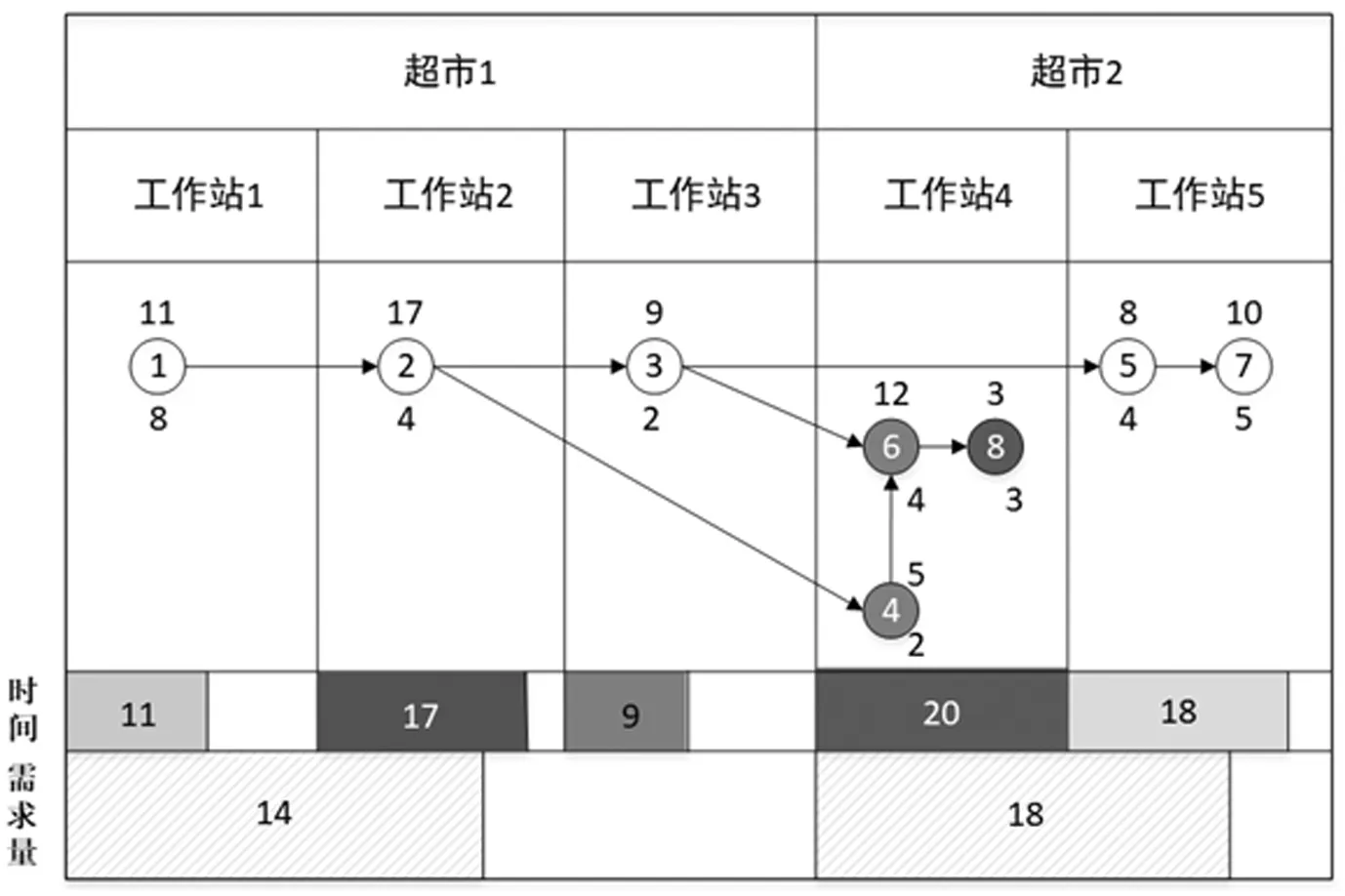
圖4 協同優化的最優裝配線平衡與物料超市規劃方案

2 混合整數規劃模型

本文用到的符號定義如下:

(1)集合與索引

N:工序集合;K:工作站集合;S:超市集合;i,j:工序,i,j∈N={1,2,…,N};k,l,m:工作站,k,l,m∈K={1,2,…,K};s:超市,s∈S={1,2,…,S}。

(2)參數

CT:生產節拍;Pij:如果工序i是工序j的緊前工序則為1,否則為0;tj:工序j的時間;dj:工序j的需求量;IC:超市的單位建設成本;SC:單位移動距離成本;xk:工作站k的橫坐標;yk:工作站k的縱坐標;xs:超市s的橫坐標;ys:超市s的縱坐標;distskl:從超市s到工作站k再到工作站l最后返回的距離;Caps:超市s的容量;KC:工作站的單位建設成本;a:工作站之間的距離;bsk:超市s到工作站k的距離;cls:工作站l到工作站s的距離。

(3)決策變量

M:最優工作站數量;Xjk:工序j分配給工作站k為1,否則為0;Zskl:工作站k到l由超市s負責為1,否則為0;NS:最優超市數量;Yk:工作站k建立為1,否則為0;Tdemkl:從工作站k到l的需求量;Wdisskl:從超市s到工作站k再到工作站l再返回的總加權距離。

(4)模型

建立的整體規劃模型如下:

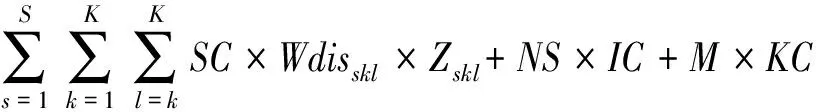
(3)

(17)

模型的目標函數(3)是最小化工作站和超市的建設成本以及總加權運輸成本,其中單位建設成本和運輸成本都轉化為單節拍下的成本;約束(4)(5)計算開啟的工作站數量和最優超市數量;約束(6)確保只有當工作站啟用了才能分配工序;約束(7)(8)保證每個工序只能分配給一個工作站,每個物料超市只能負責一段工作站的物料供應;約束(9)保證工作站是連續開啟的,避免出現工作站1、3開啟,工作站2卻未開啟;約束(10)限制每個工作站的時間不能超過節拍;約束(11)(12)分別計算每個工作站的物料需求量和一段(從k到l)工作站的物料需求量;約束(13)限制了工序之間的優先關系;約束(14)限制了超市提供的物料供應不能超過超市的容量;約束(15)確保了開啟的工作站都被超市供應;約束(16)計算了物料需求的加權距離;約束(17)限定了開啟的超市數量的取值范圍。

3 改進遺傳算法設計

本文研究的問題屬于分配問題,若采用傳統遺傳算法的兩段式編碼方式存在算子不可行、工序排列順序不直觀和算子修正難度增加的缺點。針對上述缺點,本文提出了改進遺傳算法,采用了新的編碼方式和種群初始化方法,其操作過程包括編碼、種群初始化方法、選擇算子、交叉算子、變異算子、解的修正,如圖5所示。

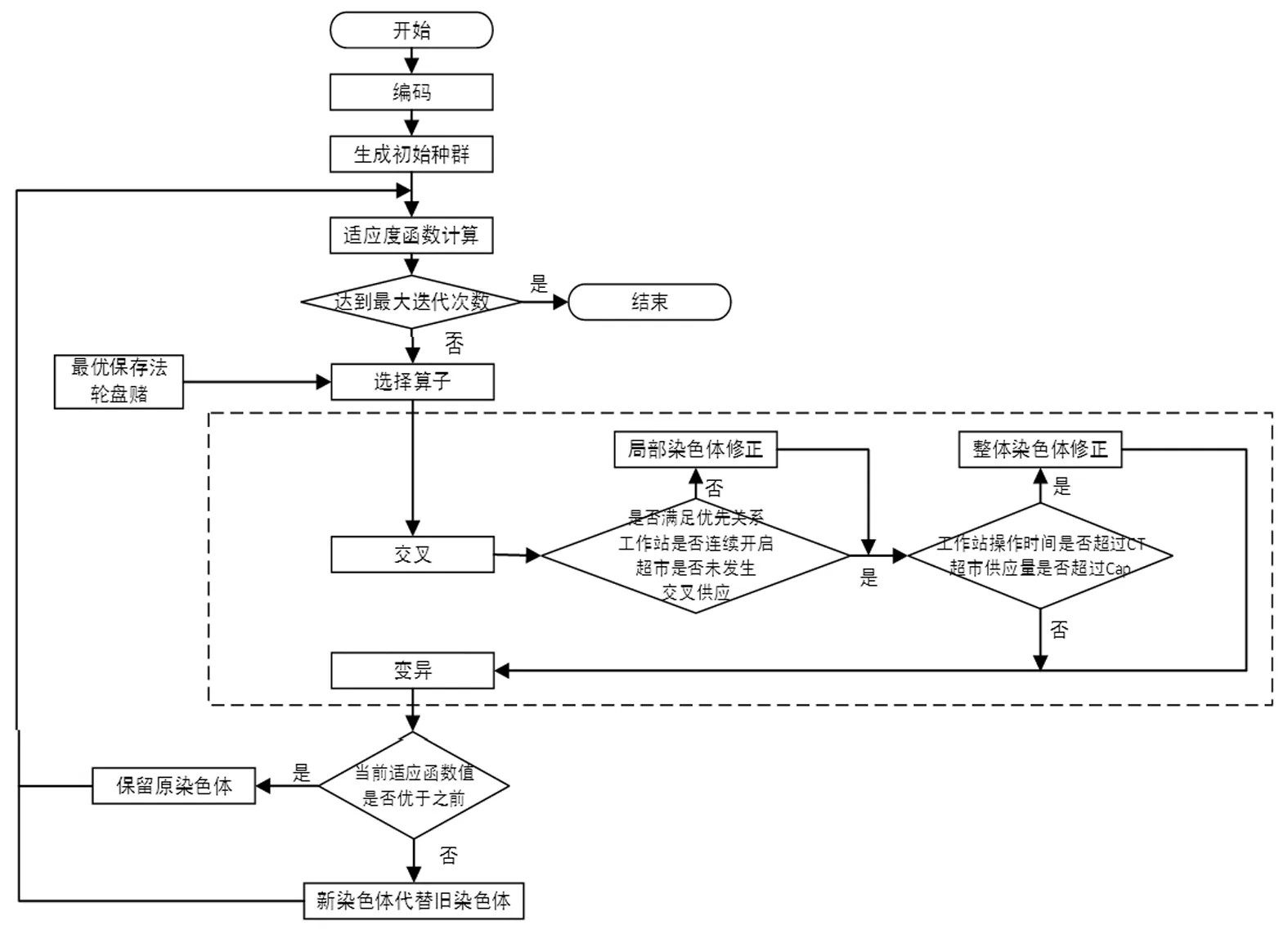
圖5 遺傳算法流程圖

3.1 編碼

本文采用三部分組成的實數編碼:根據工序優先關系形成工序序列POA,再以此得出工序的分配方案形成第二段染色體POB,其基因位與POA 的工序編號相對應,基因值為該工序被分配至的工作站的編號;第三段染色體POC 的基因位為工作站編號,基因值為該工作站被分配至的物料超市編號,0為該工作站沒有開啟。以圖1中Bowman平衡問題為例,給出了兩個染色體的編碼,如圖6所示。

圖6 編碼示例

3.2 種群初始化

本文初始種群的20%的工序分配染色體按照傳統遺傳算法生成[15],根據優先關系依次計算工序累計時間Ti,當第i工序時,Ti大于生產節拍,則將前i-1個工序分配給第1工位,依次計算直到分配完畢;另外80%染色體采用新方式生成,即根據工序的排列順序,在不超過生產節拍和最大備選工作站的前提下將工序隨機分配給工作站,并保證工作站的連續。工作站的分配是根據各工作站的工序需求量,依次計算累積作業需求量,并與物料超市容量Cap進行比較,當計算到第j個工作站的累積作業需求量大于物料超市容量時,則將前j-1個工作站分配至第1個物料超市,依次進行計算,直到分配完畢。

3.3 適應度函數構造及選擇

適應度函數的值是衡量個體優劣的指標,本文中的目標函數為最小化問題,將其轉化為最大化問題,個體p的適應度函數如式(18)所示。

(18)

本文采用的選擇方法是最優保存方法與輪盤賭相結合,為了使進化過程中的最優解不被交叉或變異操作所破壞,種群中適應度最高的n個染色體直接復制到下一代中,然后對剩余染色體進行輪盤賭選擇,適應度大的被選擇概率越高。選擇概率Sp如式(19)所示。

(19)

3.4 交叉

本文對POA采用單點交叉,對POB和POC采用雙點交叉,具體交叉過程如圖7、圖8所示。通過交叉操作之后獲得了新的染色體,但新染色體可能違反了容量或分配關系約束條件。此時需要對染色體進行整體修正以保證染色體的可行性。具體修正思路如下:以節拍限制為例,在子代1中,原先工序6、7均置于第6個工作站,工序時間總和為22,超過生產節拍,所以子代11中需修正為工序7分配到第5個工作站, 6、8分配到第6個工作站。

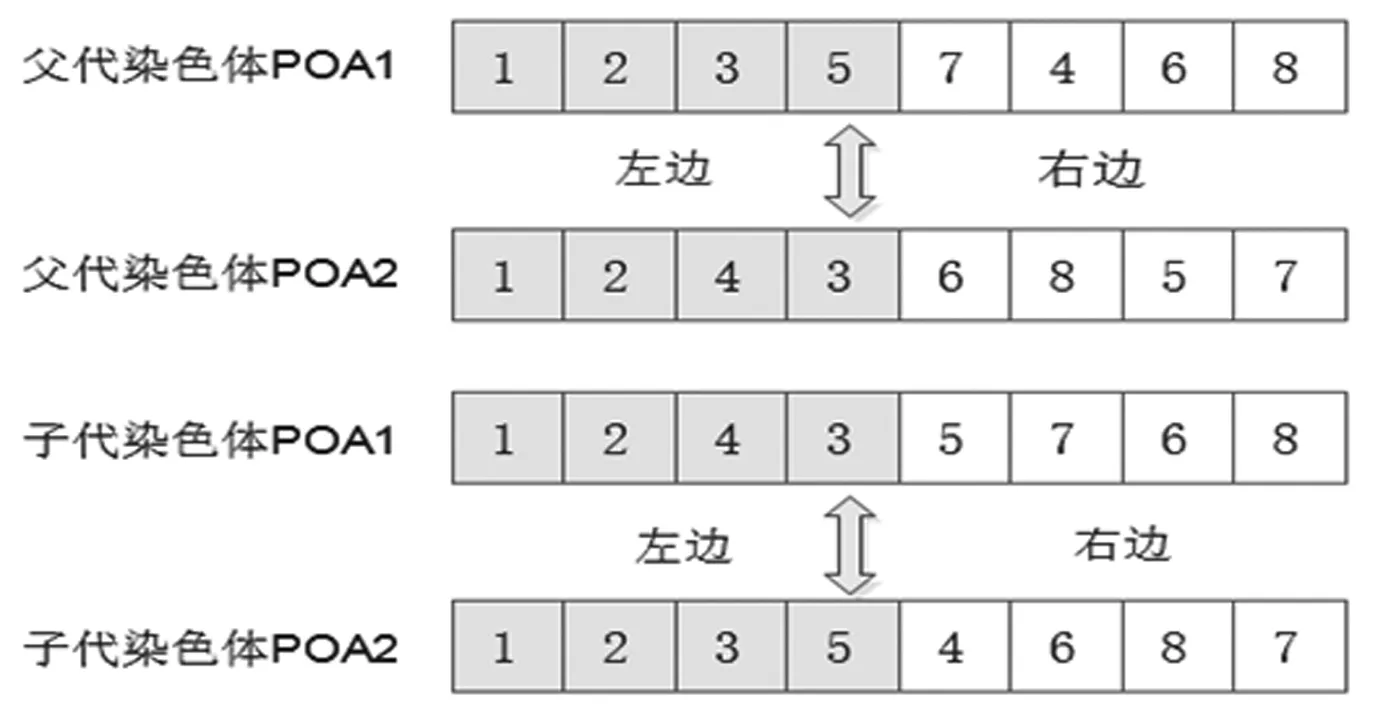
圖7 染色體POA的交叉操作

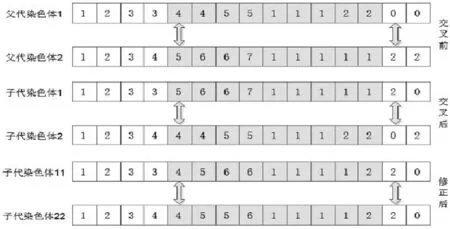
圖8 染色體POB+POC的交叉操作

3.5 變異

本文的變異操作是對三段染色體分別進行變異。染色體POA采用位移變異法,任意選擇一個基因進行變異,將進行變異的基因重新插入不違反先后關系的任意一個位置,如圖9(a)所示。POB染色體的變異方式是隨機挑選一個基因,在不超過節拍的前提下將該基因位對應的基因值隨機等于左邊基因值或右邊基因值,且工作站連續開啟。其變異操作如圖9(b)所示。為了保證工作站分配的多樣性,本文對染色體POC采用雙點變異,隨機產生兩個變異點,將兩個變異點之間的基因值在不違反相關約束的前提下隨機更換物料超市編號,其變異操作如圖9(c)所示。

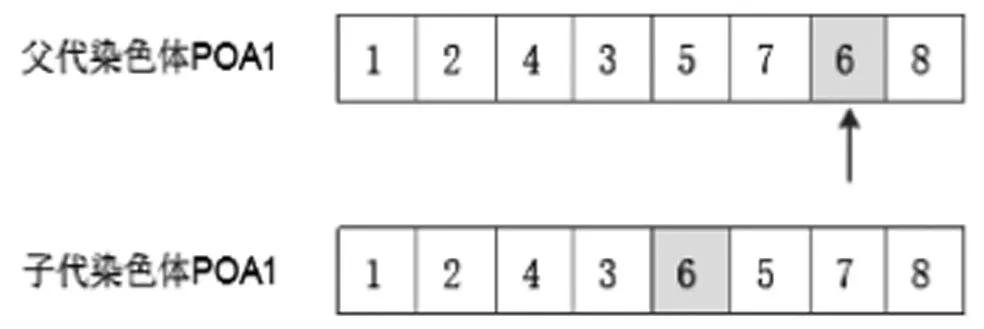
(a)染色體POA

4 算例驗證

為了驗證協同優化模型及其遺傳算法的有效性和可行性,采用了SCHOLL[16]中的SALBP1測試問題進行驗證。工作站間距為定值3,備選工作站及超市的數量為標準算例的1.2～1.5倍之間隨機生成。各工序的物料需求在1～20內隨機產生,超市至工作站距離參數需根據不同的問題規模進行設置,當超市負責一個工作站時總行程為10,之后每增加一個工作站等值遞增4,依此類推。所有測試在配置為Intel○R CoreTMi7-8250U CPU處理器進行求解。

本文的數學模型用CPLEX 12.6.1進行精確求解,最長運算時間為3600秒。遺傳算法在MATLAB R2017a中進行編程實現,種群規模為500代,最大迭代次數為100次。本文將結果與Amir[10]所提出的分階段模型求解結果進行比較,驗證本文所提出的協同優化的必要性。

協同優化的CPLEX、遺傳算法、傳統遺傳算法以及分階段方法的CPLEX運算結果如表1所示,其中M為最優工作站數量、NS為最優物料超市數量、TC為總成本。第一欄和第二欄是算例的問題和工序數量,第三欄是節拍時間CT,第四欄是超市的容量,不同的超市容量建設成本不相同[10],如表2所示。

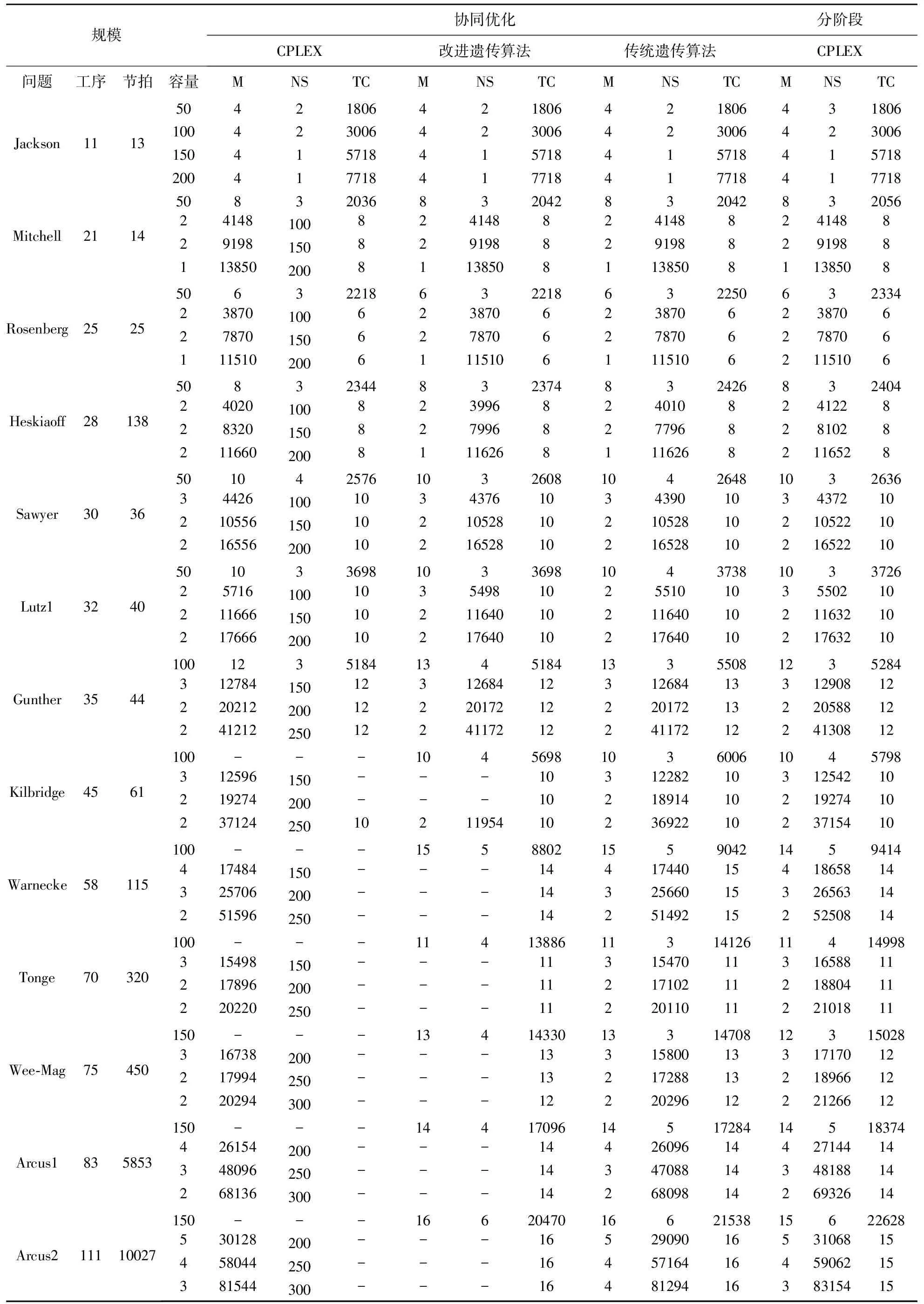
表1 運算結果分析表

表2 工作站與物料超市建設成本

由表1可知對于小規模算例,CPLEX 和遺傳算法均可在最大運行時間內找到最優解,但隨著工序數量及優先關系復雜度上升,協同優化下CPLEX無法在規定時間內找到最優解,遺傳算法可以很好的求解,證明遺傳算法有更好的適用性;通過表中的運算結果顯示,協同優化下總成本優于分階段方式下的總成本,且在工作站數量和物料超市數量方面的決策稍有不同。綜上所述,本文的協同優化方法在降低總成本方面更具有優勢;改進遺傳算法和傳統遺傳算法雖然都能找到問題的最優解和近似解,但是隨著問題規模的擴大,改進遺傳算法具有更好的性能,能在較短時間內找到更接近精確解的目標值。

圖10為傳統遺傳算法和改進遺傳算法的迭代曲線,橫坐標表示進化代數,縱坐標代表目標函數值。可以看出傳統遺傳算法的適應度值在將近60代進化后才趨于近似最優解,且極易陷入局部最優解。而改進遺傳算法隨著進化代數的增加迅速收斂,在10代左右趨于穩定,達到近似最優解,說明改進遺傳算法能夠快速收斂找到近似最優解。

(a)傳統遺傳算法

5 結論與展望

本文針對裝配線平衡和物料超市規劃這兩個相互關聯的決策問題來優化裝配線,從整體出發建立協同優化模型,并根據實際生產中的復雜性和連續性設計了適用于大規模問題的遺傳算法,可以在較短時間內獲得滿意解。與分階段方法的結果進行比較,協同優化方法在降低總成本方面更具有優勢。本文考慮的主要是直線型裝配線,在實際生產中還有其他種類的裝配線,如U型裝配線、雙邊裝配線等,未來可以根據不同的裝配線類型進行優化。同時,在現實生產中,工人的體力、精神狀態、機器設備故障、工序復雜等都會對裝配線生產活動產生影響。未來的研究可考慮從這幾個方面隨機化來進一步完善數學模型。