基于博弈論偏序集的煤礦瓦斯爆炸風險評價模型研究

賴文哲, 邵良杉

(1.遼寧工程技術大學 工商管理學院,遼寧 葫蘆島 125105; 2.遼寧工程技術大學 系統工程研究所,遼寧 葫蘆島 125105)

0 引言

煤炭資源是我國社會發展的重要基礎。目前,煤炭資源緊缺且需求量不斷增加,致使煤礦開采深度逐年遞增,這在一定程度上加大了煤礦事故發生的可能性[1]。在眾多種類的煤礦事故中,瓦斯爆炸事故具有難識別、強破壞、高死亡率等特點,這給煤炭開采工作帶來嚴重危害。因此,風險評價作為預防與控制瓦斯爆炸事故工作中的重要環節已成為研究重點。

煤礦瓦斯爆炸誘因復雜多變,樣本數據常表現出難確定、高維度等特性,這對評價方法的準確性與穩定性提出了更高要求。近年來,智能算法在瓦斯爆炸風險評價領域得到普及。施式亮和李潤求[2]首次將AHP理論引入到瓦斯爆炸事故的危險性評價中,對瓦斯爆炸的評價目標進行了修訂并給出了對應的評價標準;LI等[3]建立PSO-SVM模型為智能算法在瓦斯爆炸風險評價領域中的應用奠定了基礎;汪瑩和蔣高鵬[4]建立以RS-SVM為基礎的煤礦安全風險預測模型,雖然在大量數據支持下結果較為理想,但對于數據量的依賴性引發了方法的局限性,進而無法保證模型具備較好的穩定性;謝國民等[5]通過果蠅算法對支持向量機進行優化并建立FOA-SVM模型,進一步提高了瓦斯爆炸風險評價精度。但是,仍無法擺脫對訓練樣本的大量需求;蒲天添[6]與汪圣偉等[7]對AHP算法進行了改進并與集對分析法相結合對瓦斯爆炸風險等級作出評價,但方法過于復雜。很多研究成果在該領域仍存在少許不足,尚具有改進空間。例如,樣本自分類模式下的支持向量機等算法,雖然有較強的適用性,但在應用過程中若無大量樣本數據的支持會降低對樣本識別的準確性。模糊層次分析法,灰色評價法等雖算法簡單,但容易融入過多的主觀意愿,所得結果難以讓人信服。針對以上問題,本文首次運用博弈論法對偏序集模型中權重向量進行優化,構建博弈論偏序集模型。由此,指標權重所蘊含的信息便可在模型中體現,并且對權重精確賦值的要求便可由偏序關系替代,可有效降低計算量,且不會過多的要求數據的體量。以博弈論法對指標權重的保序性可進一步提升偏序集模型的穩定性。

1 博弈論偏序集理論

1.1 偏序集基本原理

偏序集是一種具備較強層次性的理論方法[8],揭示了集合中各元素間所處的等級與位置。應用過程中,不需了解指標權重的精確賦值,只需知道指標間重要程度的排序關系。

偏序集定義如下:

定義1[9]設R是集合A上的一個關系,若滿足:

自反性:對任意x∈A有關系xRx;

反對稱性:對任意x,y∈A,若xRy且yRx,則x=y

傳遞性:對任意x,y,z∈A,若xRy,yRz,則xRz。

則可稱R為A上的一個偏序關系。方法構建過程中通常使用“?”表示待評價集合M=(A,IC,E)的偏序關系,與A一同組成偏序集,記為:(A,?)。對?x,y∈A,有如下公式:

x≤y?cj(x)≤cj(y),j=1,2,…,n

(1)

在任意偏序集(A,?)內部,Dw(x)={y∈A|x?y}為A的劣集,Up(x)={y∈A|x≥y}稱為A的優集,N(x)為拒比集合即無法比較,且N(x)=A-Dw(x)-Up(x)。若取|Dw(x)|、|Up(x)|、|N(x)|分別表示對應集合元素個數,則有m個待選方案的(A,?)滿足:

|Dw(x)|+|Up(x)|+|N(x)|

(2)

則A中任意待選方案的高度為:

(|Dw(x)|+|N(x)|)+

(3)

(A,?)內部待選方案按照hav(x)的比較關系進行排序。

定義2[10]對于待評價集合M=(A,IC,E)所構成若矩陣Q,若第i行大于或等于第j行,便可得出AiAj即i與j對應的方案前者優于后者。由此便可得出方案間的層級關系。對于?ai,aj∈A,若aj?ai,則記作rij=1;若aj和ai不可比或ai?aj,則記作rij=0,稱R(rij)mn為(A,?)的比較關系矩陣,再通過公式(4)計算得到Hasse矩陣[11]:

HR=(R-I)-(R-I)*(R-I)

(4)

式中:HR為Hasse矩陣;R為關系矩陣;I為單位陣;*為布爾運算即(1+1=1,1+0=1,0+0=0,1×1=1,1×0=0,0×0=0)。

f(x)=ω1x1+ω2x2+…+ωnxn

f(y)=ω1x1+ω2x2+…+ωnxn

(5)

(6)

此時定理1的改進形式矩陣表示為:

(7)

矩陣Y中,當yit≤yjt(t=1,2,…,n)則有ai≤aj(i,j∈1,2,…,m)。

1.2 博弈論法優化原理

在定理1基礎上通過對多種賦權法的博弈結合,使偏序集模型中權重因子ω迅速達到最佳平衡狀態。在該平衡狀態下定理1中權重因子ω1≥ω2≥…ωn的排序關系可具備持續的穩定性,當偏序集模型中權重因子排序趨于穩定后,可用偏序關系取代原有對權重準確賦值的要求。對權重因子ω具體優化原理如下:

對于x種權重因子的最佳結合,有z個權重向量可表示為:

W(z)=[wz1,wz2,…,wzm](z=1,2,…,x)

(8)

式中W(z)表示第z種方法所得權重向量;此時,這x個權向量的線性組合可由公式(9)表示:

(9)

其中:βz為組合系數;W為向量集合。該方法以離差最小化為最終目標,對βz進行優化,得到最佳權重。離差最小化如公式(10)所示。

(10)

式中:W(c)為第c種方法所得權重。

根據最優化一階導數條件[13]:

(11)

得到矩陣形式的方程:

(12)

1.3 博弈論偏序集模型的評價步驟

Step1構建評價指標體系并劃分安全等級;

Step2構建樣本集合并對數據進行預處理;

Step3博弈優化得出最佳平衡權重,并由此確定指標權重排序轉化為偏序關系;

Step4數據累加變換得到比較關系矩陣,并轉化為Hasse矩陣;

Step5依據Hasse矩陣生成Hasse圖,以此對各樣本進行歸類與評價;

Step6結果分析,若精度達到要求則停止計算,否則應用公式(13)繼續計算秩均值并由此進行結構性解讀:

(13)

模型評價流程圖如圖1:

圖1 模型評價流程圖

2 模型的構建及實例應用

2.1 特征指標選取及風險安全等級劃分

指標體系的構建是煤礦瓦斯爆炸風險評價的重要依據,指標選取的合理性直接影響到采礦工作的安全與管理[14]。對于人因、設備、采礦環境在管理缺失的條件下隨著時間的推移將埋下安全隱患[15]。當瓦斯濃度、引火溫度、氧氣含量不斷上升達到某一臨界值時,瓦斯爆炸事故就此發生。由此,建立煤礦瓦斯爆炸事故致因過程見圖(見圖2)。

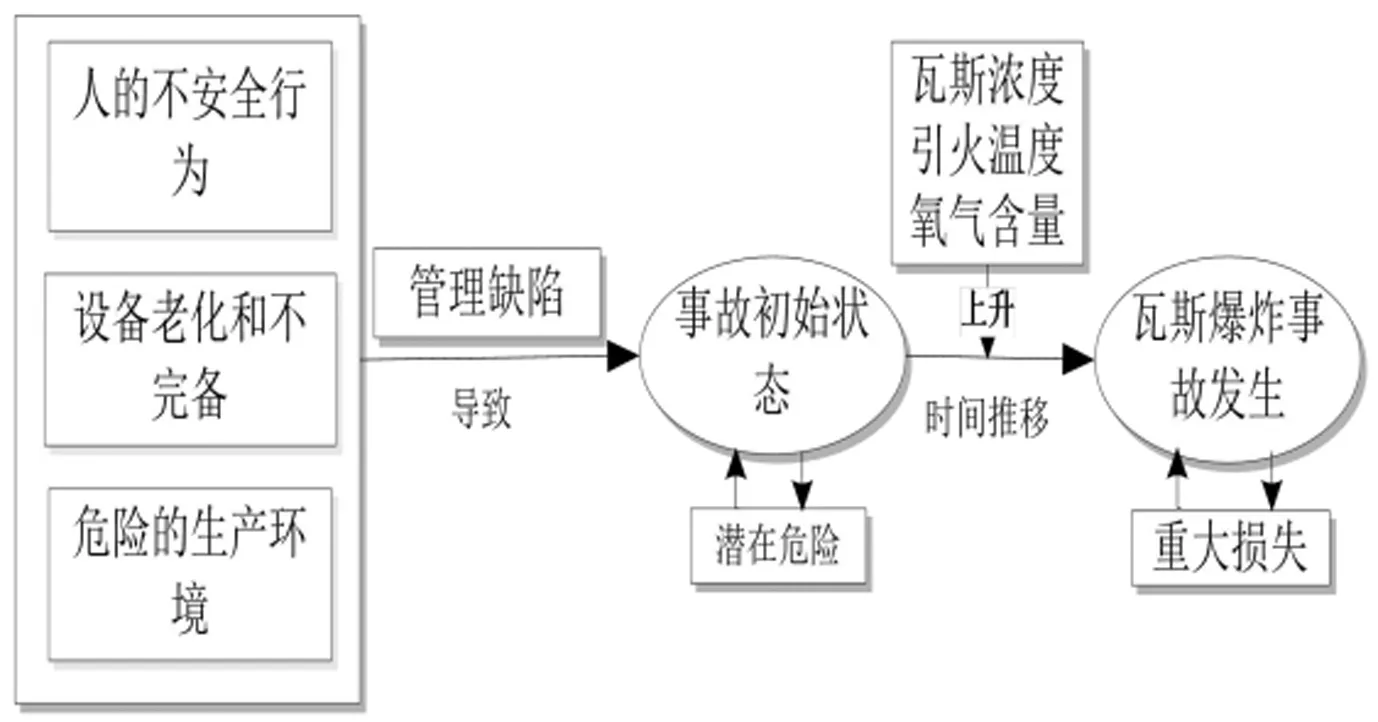
圖2 煤礦瓦斯爆炸事故致因過程圖

在圖2基礎上,結合煤礦實際生產過程中的40份瓦斯爆炸事故調查報告給出的事故致因因素進行綜合分析,最終向下篩選出通風設施設備、機電設備、瓦斯涌出量、風量供需比、安全教育與培訓等14項二級指標(記為y1-y14)構成評價指標體系。在14項指標中,存在許多綜合性指標如安全教育與培訓(y5)、防護設施(y7)、通信設施(y8)等屬于定性指標,本文中以100分制的分級形式給出。有些指標如瓦斯涌出量(y3)、瓦斯體積分數(y10)等屬于定量指標,則需根據實際的物理化學等屬性來確定。為了準確評價風險程度,本文依據危險性等級劃分標準,將瓦斯爆炸風險安全等級劃分為:(B1)不安全;(B2)較不安全;(B3)一般安全;(B4)較安全;(B5)安全。各風險安全等級所對應的評價指標數據區間見表1。

表1 各指標風險安全等級劃分區間

2.2 樣本數據選取及預處理

選取內蒙古伊泰集團下屬煤礦中具有相似災害特征的20個瓦斯礦井數據作為評價樣本(記為A1-A20),該些樣本來源于2015年數據收集。20個樣本根據上述14個評價指標(y1-y14)所對應的部分數據如表2所示。

表2 煤礦瓦斯爆炸風險評價初始數據表

為進一步評價礦井樣本所處的安全等級,本研究采用中點插值法獲得數據,并將所得到的數據作為分級樣本的對應數據。

以安全等級B1級的y1指標插值為例:指標y1在65～75范圍屬于B1等級,將65～75的區間2等分,所得插值樣本點為70;同理y1指標在75～85區間內的插值樣本點為80屬于B2等級;在85～90區間內的插值樣本點為87.5屬于B3等級;在90～95區間內的插值樣本點為92.5屬于B4等級;在95～100區間內的插值樣本點為97.5屬于B5等級。按此方法,得到其余14個指標各區間內插值樣本數據,并根據數據得到5個分級樣本:A21,A22,A23,A24,A25與上述20個評價樣本共同組成新的樣本集合。

在14個指標中y3、y9、y10均為反向指標,即數值越小屬性越優與其它指標相反,需對其取倒數處理,即1/aij。由于各指標間單位和量級不同無法直接運用,需對25個樣本數據采用公式:xij=(aij-amin)/(amax-amin)進行無量綱化處理,結果見表3。

表3 無量綱化處理結果

2.3 指標權重計算及排序

偏序集評價方法只需要獲取指標權重的排序信息進而轉化為偏序關系。本文采用較為客觀的熵權法與較為主觀的層次分析法通過公式(9)-公式(13)進行博弈結合,并對原有偏序集方法中各指標權重ω進行優化。選取前述20個評價樣本(A1-A20)進行計算并優化。優化過程的表現形式如圖3所示。

在分別應用熵權法與層次分析法計算指標權重時,部分指標未進入最佳平衡區域(即圖3圓形區域內,區域內各指標對應的權重具備保序性且越靠近圓心權重排序越靠前)且兩種方法在計算指標權重時個別指標在排序上出現歧義,產生了主客觀賦權的爭議問題。通過博弈優化后,各指標對應權重均進入平衡區域內具備了保序性,為偏序關系的轉化創造了條件,高度契合偏序集模型自身的優點。這在一定程度上解決了賦權爭議難題。由圖3的B部分所示,依據各指標所處位置與圓心距離的的大小可反饋各指標的重要程度(見表4)。

表4 比較關系矩陣各指標權重博弈排序結果

按重要程度由高到低排序為:y9>y10>y3>y4>y5>y1>y12>y11>y14>y7>y8>y2>y6>y13。指標進行排序后,以便后續得出比較關系矩陣進而轉化為Hasse矩陣。

2.4 Hasse矩陣

依據權重排序結果,對25個樣本數據(20個評價樣本與5個人為構建的分級樣本)組成的矩陣進行相應的累加變換過程,得出比較關系矩陣R(rij)mm(i,j=1,2,…,m)。矩陣中若存在aiaj的關系則可認為第i行較好與于第j行,記rij=1;若aiaj或ai與aj不可比,記rij=0,如表5所示。再由轉換公式(4)得到Hasse矩陣,如表6所示。

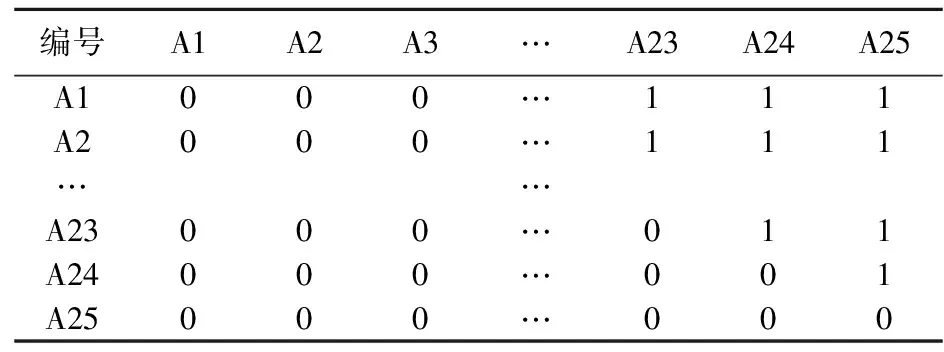
表5 比較關系矩陣

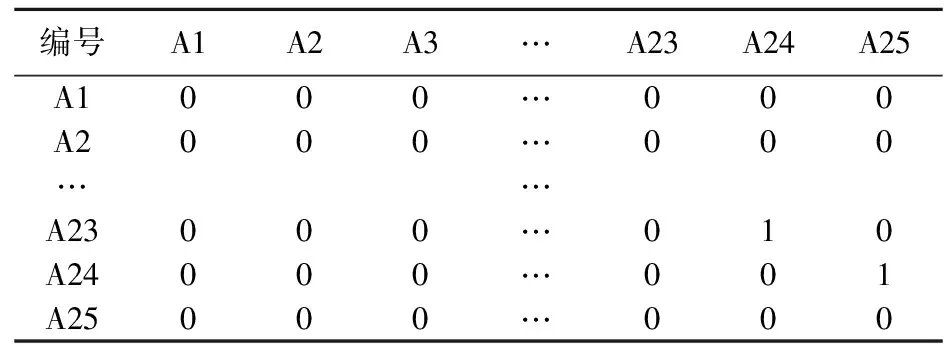
表6 Hasse矩陣

2.5 Hasse圖

依據矩陣行與列的關系生成Hasse圖,如圖4所示。通過保留最大路徑來體現出各樣本與所處層級間的對應關系,可更好的用于后續的對比與評價。

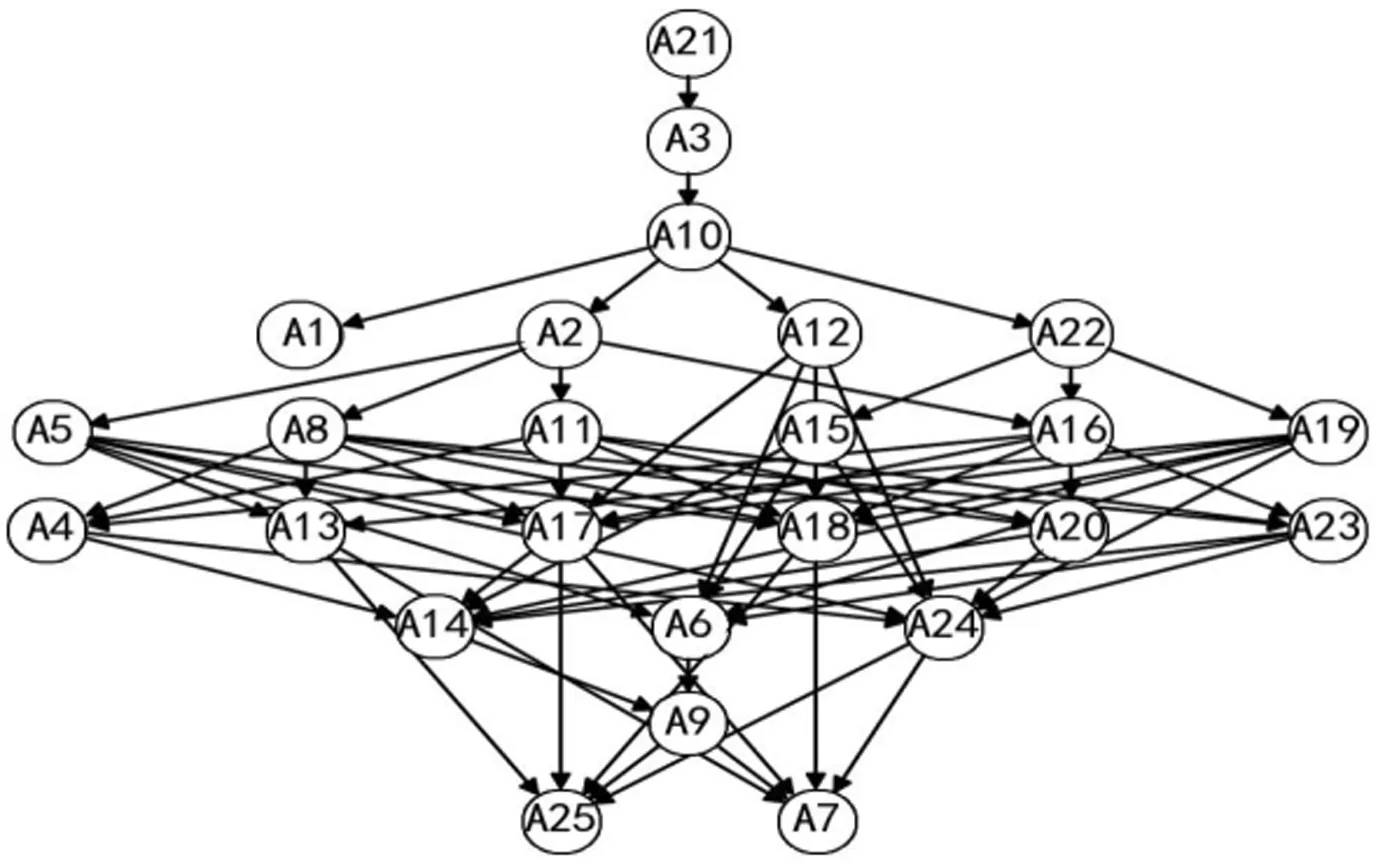
圖4 危險性等級Hasse圖

2.6 結果分析

圖4中越靠上的樣本越能表現出較強的安全性,例如圖中A2是A8的上級,表現為A2優于A8。同時,各樣本間的安全性具備相互傳遞的特點,例如A2優于A8,A8優于A4,這時可認為A2優于A4。同理可知樣本間安全性的優劣關系。

圖中的20個樣本被分級樣本劃分為五個安全等級標準群如下:

1)B5級(安全)標準群:A21、A3、A10

2)B4級(較安全)標準群:A22、A1、A2、A5、A8、A11、A12、A15、A16、A19

3)B3級(一般安全)標準群:A23、A4、A13、A17、A18、A20

4)B2級(較不安全)標準群:A24、A6、A9、A14

5)B1級(不安全)標準群:A25、A7

2.7 模型準確性與穩定性分析

通過博弈論偏序集、博弈論模糊綜合評價和支持向量機、三種模型對上述20個樣本進行評價,所得結果與實際情況的對比情況如圖5所示:

圖5 實際與評價結果對比圖

可以看出,博弈論偏序集模型評價準確性要優于另外兩種模型。在應用博弈論-模糊綜合評價模型進行風險評價時,由于瓦斯爆炸誘因復雜多變,隨著樣本量的變化指標權重值會出現波動。雖然博弈論法能確保權重值排序的穩定性,但無法滿足模糊綜合評價法對權重值精度的要求,對20個樣本進行評價時出現2處安全等級評價偏差。然而,權重排序值的穩定性卻可以滿足偏序關系的轉化條件,進而保證了偏序集模型的準確性;在應用支持向量機算法構建模型時,因訓練樣本數量較少導致訓練不充分,無法跳出局部最優解而獲得全局最優解,所得結果與實際相比往往出現偏差。

在對于上述三種模型的準確性進行對比時,因考慮到單獨一組數據與模型之間的偶合性或許難以讓人信服,故重新選出6組數據,每組數據包含10個礦井樣本所對應的指標數據,同樣采取上述三種模型進行評價并與實際情況進行對比,結果如表7所示。

由表7可以看出,相對于其他兩種方法所建立的模型,博弈論偏序集模型在對6組隨機選取的數據進行評價時準確率均保持在90%及以上,大于支持向量機、博弈論模糊綜合評價,表現出良好的穩定性,說明該模型更適用于多指標高維度下的煤礦瓦斯爆炸風險評價問題。

3 結論

(1)基于偏序集理論建立了博弈論偏序集煤礦瓦斯爆炸風險評價模型,將該模型應用于20個煤礦樣本,可以通過Hasse圖直觀地了解到各個煤礦所處安全等級,并合理的反饋出引起煤礦瓦斯爆炸事故的主導因素。經檢驗該方法所構成的模型在面對多指標高維度體系等問題時評價結果是準確且穩定的。

(2)采用博弈論法保證了指標權重排序的穩定性,在與偏序集方法結合后確保了偏序關系的轉化,且不再要求指標權重的精確賦值,整體上降低了模型對樣本數量的需求。在對煤礦瓦斯爆炸風險評價過程中具備較高的可行性,是一種較為理想的評價模型。