基于BP的隨機混合生產前沿面模型

路世昌, 劉雨詩, 于智龍, 劉 舒

(1.遼寧工程技術大學 工商管理學院,遼寧 葫蘆島 125000; 2.中國銀行保險監督管理委員會鐵嶺監管分局,遼寧 鐵嶺 112000)

0 引言

數據包絡分析(DEA)通過對多投入多產出決策單元建模,構建具有凸性、錐性及最小性的生產集合,再確定決策單元的包絡面,即生產前沿面,決策單元與生產前沿面之間的距離為無效部分,決策單元在生產前沿面上的投影為最有效的投入產出組合,從而估計決策單元的效率值。作為非參數多產多投模型,DEA模型及其擴展模型避免了對生產效率函數具體形式的依賴性,在解決實際問題時更具有普適性和實用性,被廣泛應用于政府效率評估[1,2]、銀行效率評估[3,4]、保險業效率評估[5]等多個領域,相關論文數量成指數級上升趨勢。然而,DEA模型基于確定性假設構建生產前沿面的過程中,忽略了模型中噪音、隨機誤差和環境變量等不確定因素,而實際的生產集合由非理論數據構成,常帶有誤差等其他干擾項,因此在使用DEA模型估計實際生產集合的效率時,生產前沿面極易受到特異數據影響而偏移。

針對這一問題,學者們從不同角度給出了解決辦法。馬生昀等[6]利用隨機規劃方法構建了參數或決策單元服從一定概率分布的DEA隨機擴展模型,王美強和李勇軍[7,8]利用模糊數學方法量化非確定性變量構建DEA模型,在模糊環境下形成模糊生產前沿面,KUOSMANEN等[9]和謝輝軍等[10]通過DEA模型與隨機前沿面分析(SFA)結合的方式進行數據分析,增加模型的隨機性。上述方法中,隨機規劃方法需依賴于特定參數或概率分布,模糊數學方法中模糊數的轉化效果直接影響模型效率評估結果,在與SFA結合的方法中只能將誤差歸因于一個投入或一個產出變量上。

近幾年,由于機器學習算法在處理不確定性問題上具有一定優勢而成為數據處理的主流方法,將DEA模型與機器學習算法結合使用,能夠實現對具有多重特征且不確定性數據的分析,減少對特定參數或概率分布的依賴,形成具有可擴展性的集成模型。其中,神經網絡算法在處理多維、復雜數據上具有優勢,在與DEA模型結合時效果更為突出,被越來越多的學者選擇使用[11,12]。目前在DEA模型與神經網絡算法結合的方法中,一般選用投入或產出數據作為自變量,已生成的效率值作為因變量,進行回歸分析,實現效率值的校正,模糊了DEA模型中包絡面與決策單元之間的關系。馮長敏等[13]根據DEA模型中決策單元在生產前沿面上的投影值,利用BP神經網絡重新估計生產前沿面并實現了決策單元的排序。但僅通過決策單元有效值進行再估計,極大的依賴原有生產前沿面,易受到特異數據影響。

本文考慮構建一種隨機混合生產前沿面(BP_SHPF)模型,將有效決策單元與貼近生產前沿面的無效決策單元分組混合,通過BP神經網絡訓練,確定新的生產前沿面位置,并根據新建立的生產前沿面估計決策單元效率值。BP_SHPF模型通過BP神經網絡避免了非機器學習方法的局限性,同時保留了決策單元與生產前沿面的位置關系,校正了生產前沿面前置問題,在對實際生產集合進行效率評估時得到更易區分、更合理的決策單元效率值與效率排序。

1 BP_SHPF模型

BP_SHPF模型流程如圖1所示,主要包括以下4個步驟:求解確定生產前沿面;混合有效單元與無效單元;神經網絡訓練;重新計算決策單元(DMU)效率。

1.1 DEA模型求解確定生產前沿面

BP_SHPF模型作為一種集成模型,適用多種DEA模型。本文將以DEA模型中的BC2模型為例說明BP_SHPF模型的構建方法。BC2模型能夠在變動規模報酬下實現純技術效率與規模效率的評估,其生產可能性集為pB={(x,y)|x≥Xλ,y≤Yλ,eλ=1,λ≥0},其中,條件eλ=1為凸性約束條件,減少了模型的可行域范圍。

下面以面向產出的BC2模型為例:

(BCC-O0) maxηB

s.t.Xλ≤x0

ηBy0-Yλ≤0

eλ=1

λ≥0

如圖2所示,BC2模型構建了生產前沿面A-B-C,生產前沿面上的決策單元為有效單元,效率值為1,其他無效決策單元在生產前沿面上的投影為該決策單元的有效值,BC2模型中投影值計算如下所示:

圖2 BC2模型生產前沿面

根據投影值可計算決策單元效率,公式如下:

BCCefficiency=DT/ST

1.2 混合決策單元

如圖3所示,BP_SHPF模型為增加DEA模型隨機性,減少特異數據影響,認為位于生產前沿面附近的決策單元仍有一定概率是有效決策單元,將這些決策單元與有效決策單元混合,重新生成生產前沿面,將一定程度改善DEA模型生產前沿面前置情況。

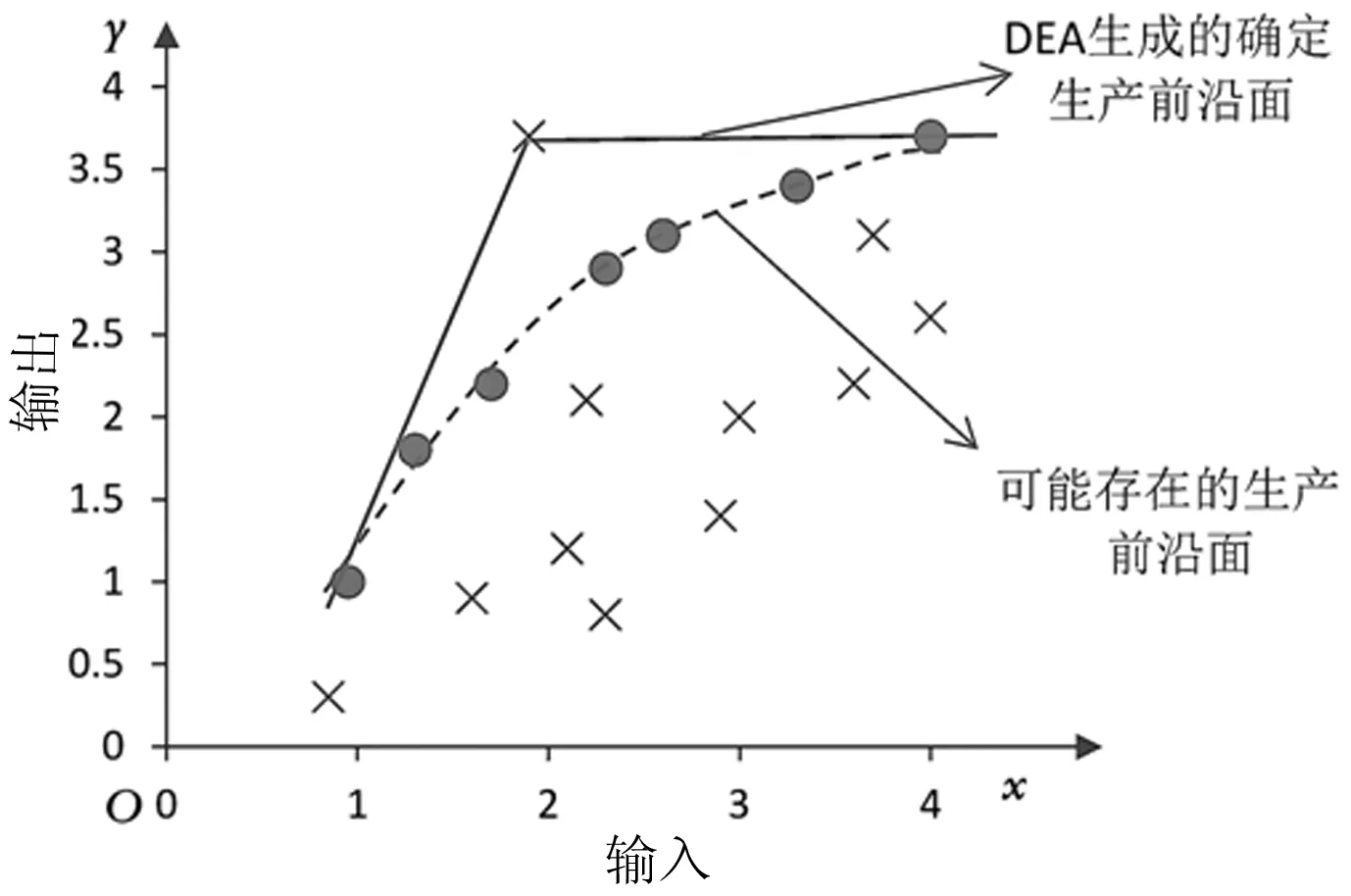
圖3 特異數據影響生產前沿面

在投入集合X中,投入相近的決策單元的效率評估應采用同一參考標準,因此本文將采取分段最優方法進行數據混合,算法過程描述如下:

(1)將投入集合X按序均分為N個子集合記為Xn,并將子集中包含最多的有效決策單元數記為m。

(2)對第n個子集內的決策單元按效率降序排列,取效率最大的m個決策單元,標記為混合單元集合S。

(3)計算各子集中混合決策單元平均效率Pn,比較求得全部子集的最低混合決策單元效率P′。

(4)對任意非最低效子集Xn,將效率降序排序m+1至m+a個決策單元添加至集合S,使得Pn≤P′且S是Xn內決策單元效率均值最大的子集。

1.3 BP神經網絡訓練

本小節將混合決策單元集合的投入值作為輸入,產出值作為輸出,進行BP神經網絡訓練,通過誤差反向傳播進行各層神經元參數調整,實現集合X的期望產出值估計。BP神經網絡最終目標是誤差最小化,通常采用梯度下降算法,按誤差梯度反向調整神經元參數,一定程度存在無法獲得全局最優、學習效率低、收斂速度慢及理論依據不足等問題。為此許多學者提出了BP神經網絡優化方法,包括隨機梯度下降、擬牛頓法、自適應梯度算法、共軛梯度法等。本文采用自適應梯度算法訓練神經網絡,學習速率根據誤差大小調整,無需設定,使神經元參數向誤差減小方向調整,算法過程簡述如下:

1)構建BP神經網絡net包括X個輸入,H個隱藏單元,Y個輸出;

2)初始化神經網絡權值w;

4)與n-1次迭代誤差進行比較,若E(n)E(n-1)則減小學習步長η(n)=η(n)×b,b∈(0,1);

5)net權值與步長η(n)存在以下關系w(n+1)=w(n)-η(n)×(δE(n)/δw(n));

6)重復步驟1至步驟5直到誤差值小于預設誤差或實驗迭代次數滿足要求。

BP_SHPF模型中神經網絡結構如下:

神經網絡層數:多位研究學者通過理論及實踐得出,具有單隱藏層的BP神經網絡能夠逼近閉區間的任意連續函數,因此BP_SHPF模型使用如圖4所示的“輸入層—隱藏層—輸出層”三層結構神經網絡訓練數據集。

圖4 三層結構神經網絡

輸入輸出節點數:神經網絡模型目標是校正生產前沿面位置,輸入、輸出結點數應與DEA模型中投入、產出數相對應。

隱藏層節點數:隱藏層節點數是直接影響神經網絡準確性的重要參數,對于三層神經網絡結構而言,隱藏節點數H過大會導致過擬合,H過小會導致誤差較大。本文假定隱藏層節點與訓練樣本數量和輸入輸出數存在以下關系:

其中,H為隱層節點數,X為輸入個數,Y為輸出個數,a為常數[1,10]。在實驗過程中對a取1至10的整數,計算對應的H值,并分別進行神經網絡訓練,計算每次訓練對應總誤差Ea,比較Ea大小,選取Ea最小時的H值作為實際隱層節點數。

1.4 決策單元效率再計算

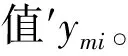
決策單元m的實際產出值與生產前沿面上產出值的距離為該決策單元的無效部分。如圖5所示,在DEA模型中決策單元的效率通過原生產前沿面A-B-C-D上的投影點F計算,在BP_SHPF模型中構建了新的生產前沿面A-B-E-D,決策單元m的效率通過投影點G計算。

2 實驗結果

2.1 Monte Carlo模擬

本節通過Monte Carlo模擬對BP_SHPF模型分別進行單產單投及多產多投驗證。

(1)單產單投模型

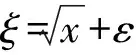
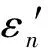
實驗中隨機生成兩個樣本數據,數據大小分別為N=100,N=300,重復實驗次數M=100,實驗結果如圖6、圖7所示。其中,“*”為DEA模型生成的前沿面,“+”為DEA_BP模型,即BP僅對有效決策單元校正結果,“◆”為BP_SHPF模型生成的前沿面,“▲”為計算目標值ξ,折線為實際目標值′ξ,可以發現DEA模型前沿面存在明顯前置,DEA_BP模型增加了前沿面的隨機性,但并不能有效校正前沿面,甚至出現有效值高于DEA模型的情況,而BP_SHPF模型通過生成光滑非線段構成的生產前沿面,有效的校正其前置問題,更貼近真實情況。

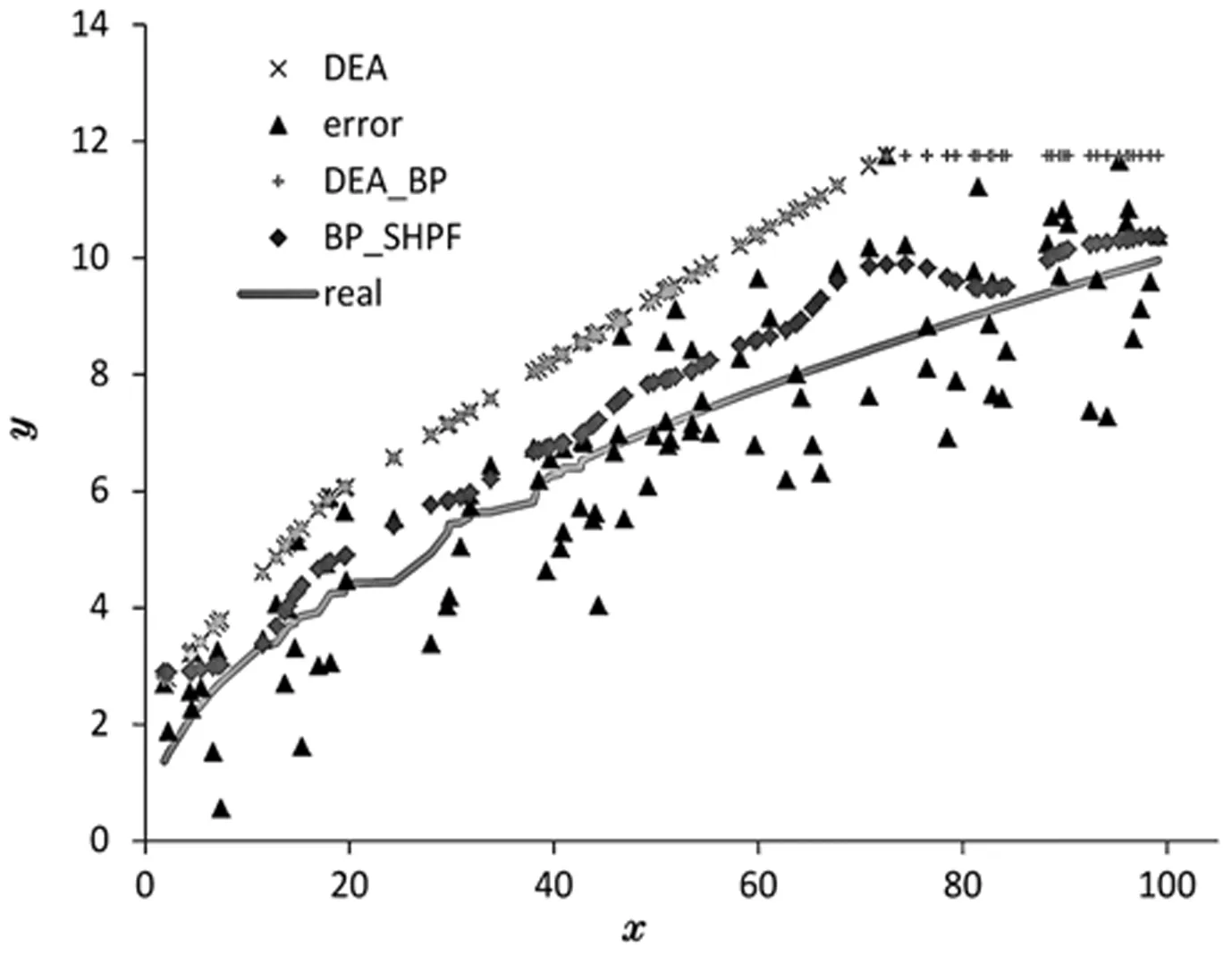
圖6 N=100投入產出估計結果

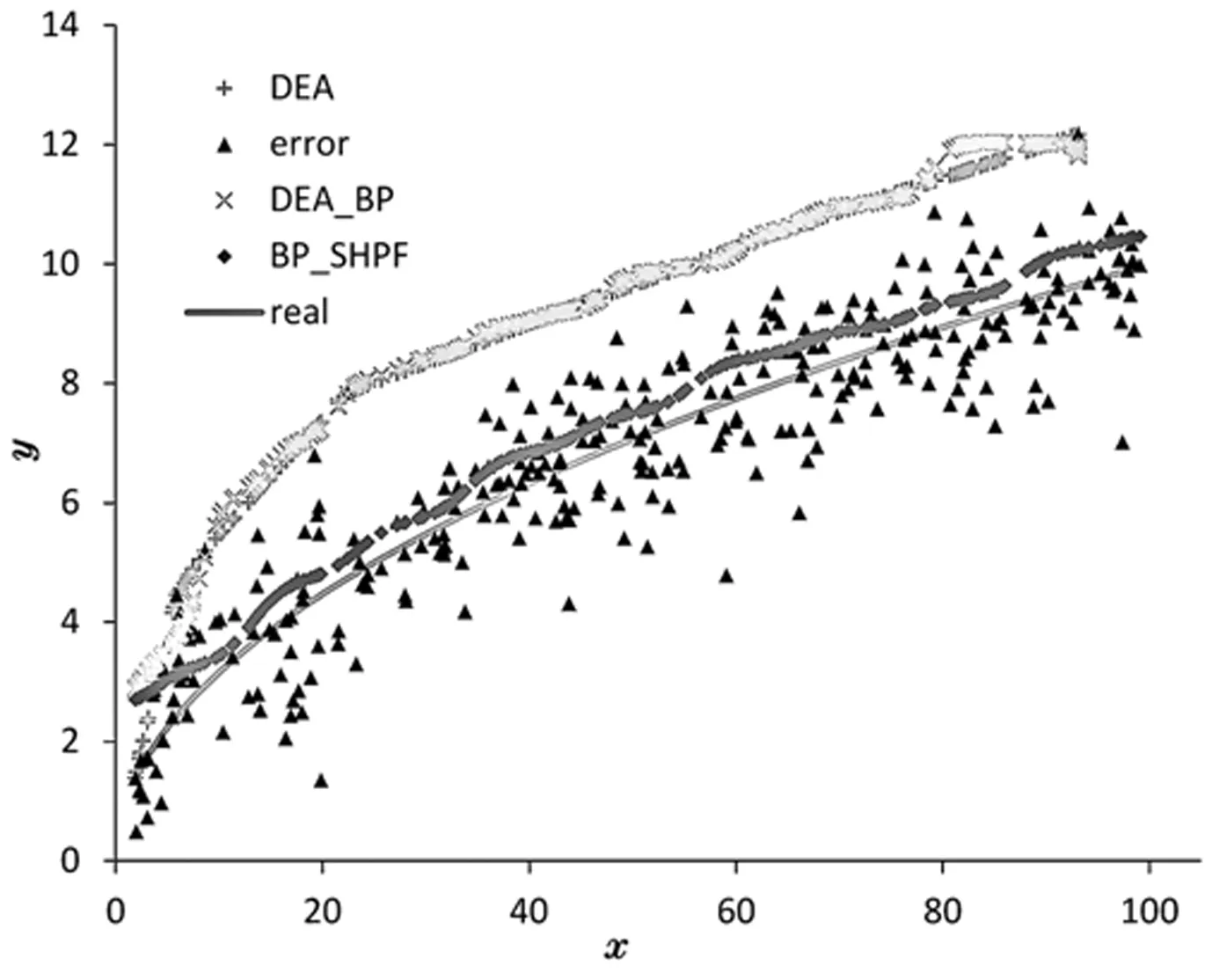
圖7 N=300投入產出估計結果

模型誤差結果比較如表1、表2所示,表中E為各模型誤差均值,MSE為均方誤差,BIAS為偏差。對比表中結果可以發現,BP_SHPF模型MSE和BIAS均明顯小于DEA和DEA_BP模型,BP_SHPF模型一定程度上有效,且樣本數量N=300時BP_SHPF模型MSE和BIAS值小于N=100,說明隨著樣本數量增加,BP_SHPF模型估計效果有所提升。

表1 N=100單產單投E、MSE、BIAS值

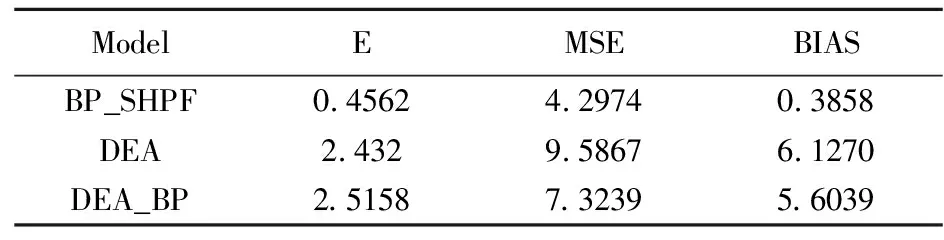
表2 N=300單產單投E、MSE、BIAS值

(2)多產多投模型

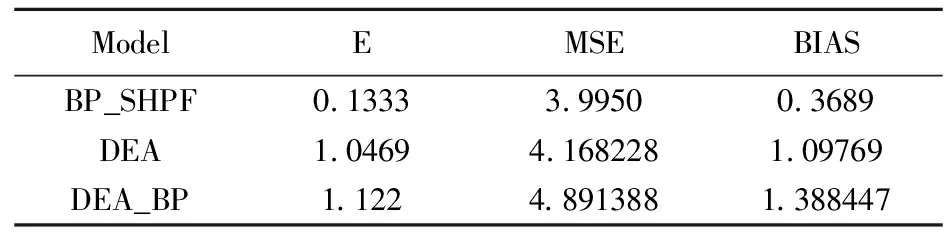
表3 N=100多產多投E、MSE、BIAS值

表4 N=300多產多投E、MSE、BIAS值

2.2 Spearman 秩相關分析

本節通過Spearman秩相關分析驗證BP_SHPF模型計算的效率值與傳統DEA模型計算的效率值的相關性,證明BP_SHPF模型效率排序有效。根據第3節中BP_SHPF模型與傳統DEA模型實驗結果計算決策單元效率并按降序排列,記為序列X,Y。令Pi為序列X中Xi的秩,Qi為序列Y中Yi的秩,使用參數Bi=Pi-Qi表示兩者排序的一致性,則Spearman相關系數可以計算如下:

Spearson相關系數計算結果如表5所示,可發現單產單投BP_SHPF模型與DEA模型相關性系數均大于0.8,多產多投BP_SHPF模型與DEA模型相關性系數均大于0.5,認為兩者存在相關性,BP_SHPF模型效率排序可靠。

表5 Spearman相關系數

3 107家農村商業銀行生產效率分析

本節將BP_SHPF模型應用于中國農村商業銀行效率分析與排序,共收集135家農村商業銀行2010年至2018年數據,數據來源為國泰安金融數據庫CSMAR及銀行機構按規定披露的財務報表。由于農村商業銀行公司治理能力弱,部分銀行年度報表數據存在缺失現象,對數據進行整理后共獲得2014年至2018年107家農村商業銀行數據用于模型實證分析,按地區對其進行分類,其中東部地區64家,中部地區36家,西部地區7家,資產負債情況如表6所示。依據謝建輝等[10]實驗數據選擇,本文選用營業支出、管理費用支出作為投入變量,利息收入和其他收入為產出變量,分別通過BP_SHPF模型和DEA模型計算得出2018年各地區農商行效率均值及標準差如表6所示。實驗結果表明,BP_SHPF模型和DEA模型計算的效率均值大小排序一致,均為東部地區農商行效率均值大于西部地區農商行效率均值大于中部地區農商行效率均值。但DEA模型得出的各地區間農商行效率均值差距不明顯,東、中地區農商行效率均值差和東、西地區農商行效率均值差分別為0.0365和0.0046,BP_SHPF模型計算東、中地區農商行效率均值差和東、西地區效率農商行均值差分別為0.1818和0.0512,更好的體現了各地區農商行間效率差距。通過實驗得出的效率標準差可以發現,經BP_SHPF模型處理后,同一地區決策單元效率值的標準差大于DEA模型,這表明同一地區的農商行效率值更加分散,更好的體現了農商行之間的效率差距。

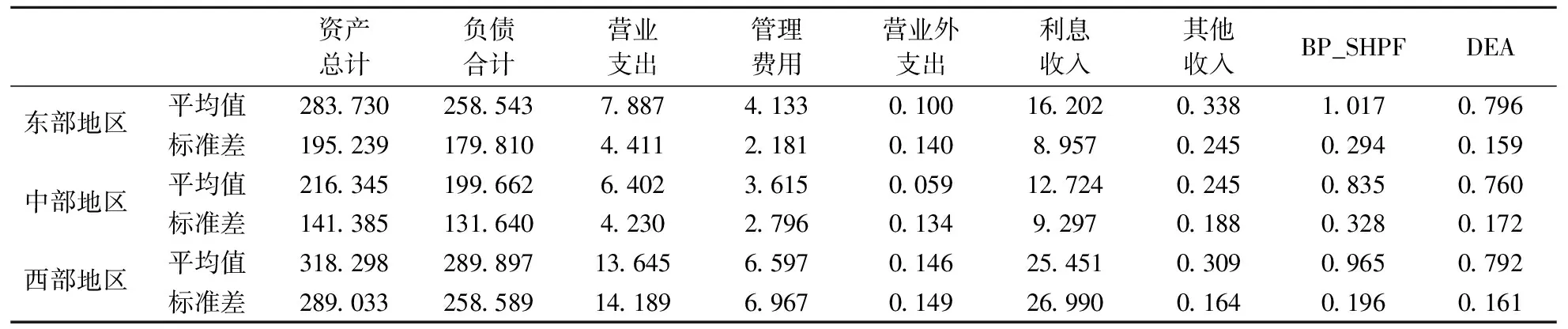
表6 東、中、西部地區銀行機構投入、產出及效率均值

圖8表示了2014年至2018年期間東、中、西部地區農商行效率變化情況。總體上,2014年至2018年期間東部地區農商行效率均值最優。各地區農商行效率均值呈現先上升再下降后趨于平穩狀態,其中,東、西部地區農商行效率均值于2015年達到峰值,中部地區農商行效率均值于2017年達到峰值。值得注意的是2014年至2015年西部地區農商行效率均值明顯提升,2016年至2017年中部地區農商行效率均值呈現明顯上升,但2018年出現急速回落。

圖8 東、中、西部地區年度效率均值

4 結論

在DEA模型的基礎上,本文假設貼近生產前沿面的無效決策單元一定概率有效,通過對生產前沿面的后置校正,改善特異數據對生產前沿面的影響,并通過Monte Carlo模擬實驗驗證模型在單產單投及多產多投生產集合上的效率評估,并證明模型能有效校正DEA模型誤差,使用Spearman相關系數分析BP_SHPF模型估算效率與傳統DEA模型估算效率的相關性,證明其效率值及效率排名有效。同時,對107家中國農村商業銀行效率進行評估,體現BP_SHPF模型具有可用性和實用性。

BP_SHPF模型是一種效率評估方法,其中所使用的BP神經網絡主要用于生產前沿面重置,在使用過程中可以嘗試用其他機器學習算法進行替代,進一步將模型擴展為DEA模型與機器學習算法結合的集成模型。在實驗過程中發現,如數據存在指標為負或數據缺失等數據問題時,則無法使用BP_SHPF模型,如何對不完全數據進行效率分析將是進一步的研究方向。