考慮半剛性連接的輸電塔結構離散優化設計方法

李正良，彭思思，王濤,2

（1. 重慶大學 土木工程學院，重慶 400045;2.哈爾濱工業大學 交通科學與工程學院，哈爾濱150090）

隨著國家輸電電網建設步伐的加快以及電網工程向著特高壓不斷升級[1]，輸電線路的要求日益提高，不僅要考慮結構的安全性，更要考慮其經濟性。輸電塔作為輸電線路的重要組成部分，其用鋼量大、工程造價成本占比高，對其進行結構優化設計具有重要現實意義和經濟效益。

1971年Beck等[2]敘述了計算機對輸電線路設計產生重要影響，此后，基于計算機的輸電線路優化設計得到了極大拓展，國內外學者將不同優化方法應用于輸電塔優化設計領域，對輸電塔塔身、塔腿、斜材等的截面、形狀、拓撲以及組合優化設計展開大量研究[3-11]，相關研究成果頗豐：Taniwaki等[3]探究了包含218根桿件的輸電塔整塔在靜載和地震荷載作用下的組合優化問題；Rajeev[4]、王藏柱[5]、郭惠勇[6-7]等對除塔頭以外的輸電塔塔身進行優化設計；張卓群等[8]研究了輸電塔塔身局部截面、形狀、拓撲和組合優化問題；鄧洪洲[9]等提出了針對輸電塔交叉斜材的拓撲優化方案；崔磊[10]、郭惠勇[11]等采用不同優化算法實現輸電塔下部塔腿的拓撲優化設計。在輸電塔結構優化設計中，通常假定桿件之間的連接為鉸接進行計算，在實際工程中，由于輸電塔節點板連接處螺栓群和節點板共同受力并產生剪切變形，節點的受力特征往往介于二者之間，即半剛性連接。與鉸接的零剛度以及剛接的無窮大剛度不同，輸電塔的半剛性連接節點具有一定轉動剛度，因此在受力變形過程中能夠傳遞部分彎矩，且產生一定相對轉角，這種半剛性力學特征會對輸電塔整體受力性能產生不可忽視的影響。

為考慮連接節點的半剛性特性對輸電塔結構受力-變形的影響，王朋等[12]探究了角鋼輸電塔螺栓滑移性能及其對輸電塔的受力-變形特征的影響；Jiang等[13]針對不同節點的連接剛度，總結了構造節點對輸電塔動靜態特征的影響規律；安利強等[14]采用一種剛度可調的半剛性連接單元模擬特高壓鋼管塔節點連接，分析了半剛性節點對鋼管塔靜力特征的影響；錢程等[15]提出考慮節點半剛性連接對輸電塔自振特征和風致響應的影響，表明考慮半剛性連接的輸電塔模型更為合理。

綜上所述，輸電塔結構中不宜簡單忽略半剛性節點的影響，但目前考慮半剛性連接輸電塔的相關研究仍較少，尤其考慮半剛性連接的輸電塔結構優化設計現有文獻更少。筆者建立了考慮半剛性連接的輸電塔有限元模型，提出考慮半剛性連接的輸電塔優化數學模型，進而基于粒子群優化(PSO)算法發展了一種考慮半剛性連接的輸電塔離散優化設計方法。

1 考慮半剛性連接的輸電塔有限元模型

以沿海地區某220 kV角鋼輸電塔為例，其結構如圖1所示。該塔高60.4 m，根開10.56 m，水平檔距350m，垂直檔距為550 m。

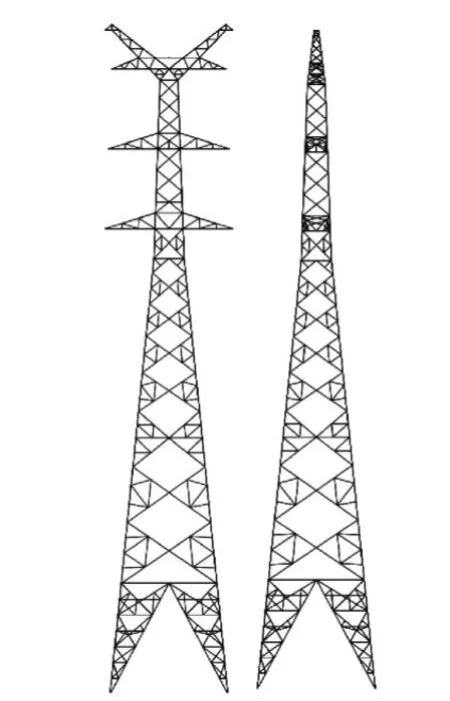
圖1 輸電塔K形節點構造示意圖Fig. 1 K-joint of transmission tower

筆者采用ANSYS軟件建立輸電塔有限元模型，其中輸電塔桿件采用BEAM單元進行建模，桿件采用理想彈塑性本構關系模型，鋼材密度為7 850 kg/m3，彈性模量為2.06×105MPa，屈服強度設為345 MPa。輸電塔所受荷載包括永久荷載以及可變荷載，其中永久荷載主要為輸電塔塔身構件的自重荷載以及導線、地線的重力荷載，施加在輸電塔有限元模型的可變荷載主要包括塔身的風荷載、導地線傳至塔身的風荷載和金具絕緣子的風荷載。

為考慮半剛性連接對輸電塔結構的影響，通過輸電塔半剛性節點的彎矩-轉角(M-θ)關系描述其力學性能，采用參考文獻[16-17]中提供的角鋼輸電塔半剛性節點彎矩-轉角(M-θ)曲線，如圖2所示。為簡化計算，有限元模型中各半剛性節點在X、Y、Z方向上的空間轉動均采用同一條M-θ曲線[18]。

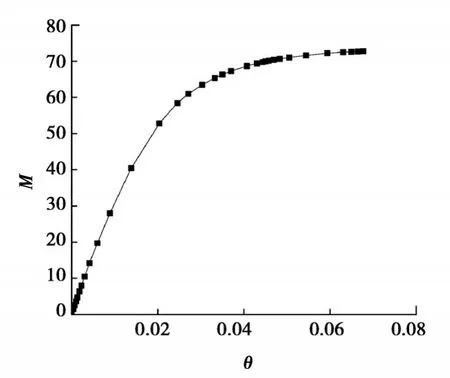
圖2 半剛性節點的M-θ曲線Fig. 2 The M-θ curve of semi-rigid joints

在考慮半剛性連接的輸電塔有限元模型中，將圖1 所示的輸電塔塔身部分主材與交叉斜材的連接節點視為半剛性連接，其連接處簡化模型如圖3所示，使用COMBIN39彈簧單元模擬半剛性節點的力學行為，可通過定義實常數輸入節點的彎矩-轉角曲線。

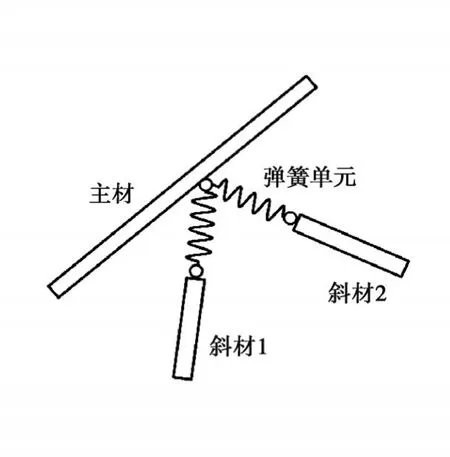
圖3 K形節點有限元模型Fig. 3 The finite elements model of K-joint

2 考慮半剛性連接的輸電塔優化數學模型

對考慮半剛性連接的輸電塔進行離散優化設計，其目的是在滿足各項要求前提下，實現結構輕量化、經濟化設計。在對輸電塔結構進行優化設計前，首先建立相應的優化設計數學模型。

2.1 優化設計變量

優化設計變量的選取即確定自變量及其取值范圍。在考慮半剛性連接的輸電塔優化問題中，對輸電塔除塔頭以外塔體部分的主材桿件進行截面優化設計，故優化設計變量為輸電塔塔身主材構件截面尺寸，其取值是不連續的，可以根據不同主材截面所采用的型鋼種類，將其設為多個離散設計變量。每個設計變量的取值需滿足

式中：n為設計變量個數；優化設計變量X={x1,x2,…,xn}；Si為第i個離散變量的取值集合，一般來源于常用的輸電塔角鋼型號表。

2.2 優化目標函數

優化設計目標函數是以設計變量為自變量的函數表達式，函數值應與自變量的取值對應。對于輸電塔塔架結構，其工程造價主要來源于結構的鋼材用量，故在滿足結構安全性的前提下，造價成本成為了設計人員主要的考慮因素。在考慮半剛性連接的輸電塔離散優化設計中，為降低成本、節省材料，以結構桿件的總質量作為優化目標函數，即

式中：W表示輸電塔桿件的總質量；n為設計變量總數，即優化中主材桿件數目；ρi為第i根桿件的材料密度，統一取鋼材密度ρ=7 850 kg/m3；Ai為第i根桿件的橫截面面積；li為第i根桿件的計算長度。

2.3 約束條件

為了防止輸電塔塔身主材構件發生強度破壞，保證結構的安全使用，荷載作用下的桿件應力絕對值不應大于材料的容許應力值，故桿件應滿足下列應力約束條件

式中：σi表示第i根桿件的應力；Ni表示第i根桿件的軸力；Ai為第i根桿件的橫截面面積；φi為第i根桿件的穩定系數；[σ]i為第i根為桿件的容許應力值，可通過調節容許應力值使設計的半剛性連接輸電塔結構具有一定安全裕度。

同時，為保證結構正常使用，在荷載作用下輸電塔整體結構應具有足夠剛度，限制結構的最大位移絕對值不大于給定的位移上限值，故變形約束條件為

式中：umax為荷載作用下考慮半剛性連接輸電塔結構產生的最大位移；[u]為給定的容許位移值。

2.4 優化數學模型

對于考慮半剛性連接的輸電塔離散優化設計問題，其數學模型可寫為如下形式

式(5)所示的輸電塔經濟性優化設計數學模型中給出了設計變量約束條件和狀態變量約束條件，得到最優設計結果既能滿足所有的約束條件又能得到最小的目標函數值，實現結構的安全性指標，同時保障了經濟性。

3 半剛性連接的輸電塔離散優化設計方法

3.1 優化算法

在考慮半剛性連接的輸電塔離散優化設計中，采用計算簡單、易于實現的粒子群優化(particle swarm optimization，PSO)算法[19]進行尋優，通過MATLAB軟件編寫基于代理模型的離散優化設計算法程序，其中PSO算法參數設定如表1所示。

表1 PSO算法參數值Table 1 The parameter values of PSO algorithm

在式(5)所示的優化數學模型中，應力約束條件和變形約束條件是與設計變量相關的狀態變量約束條件，對于該約束優化問題，需進一步采用罰函數法計算優化目標函數的適應度值。定義罰函數P(x,a)為

式中：系數a被稱為懲罰系數，通常為一個很大的正數；h1(x)和h2(x)可分別如下計算

進而，PSO優化算法中適應度函數F(x)為

3.2 考慮半剛性連接的輸電塔優化設計流程

對考慮半剛性連接的輸電塔進行截面優化設計（如圖4所示），即改變結構桿件的截面尺寸，尋找滿足約束條件的最優截面面積，使構件的應力接近滿應力狀態，實現材料的充分利用。

圖4 考慮半剛性連接的輸電塔離散優化設計流程Fig. 4 Discrete optimization flowchart for transmission tower with semi-rigid joints

基于半剛性連接的輸電塔離散優化設計方法的流程如圖4所示，其具體步驟為：

1)建立基于半剛性連接的代理模型優化設計的數學優化模型，確定離散優化設計變量x、約束條件以及優化目標函數W；

2)獲取輸電塔連接節點的實際彎矩-轉角曲線；其次在ANSYS軟件中采用彈簧單元模擬半剛性連接節點的力學行為，建立考慮半剛性連接的輸電塔有限元分析模型；然后設置輸電塔有限元模型中單元屬性、網格劃分、接觸單元、荷載大小、非線性分析等相關參數，計算輸電塔的結構響應；

3)采用粒子群算法求解離散優化問題：初始化優化算法參數后，在設計空間中抽取一定數量的初始樣點X0={x1,x2,…,xn}，通過有限元模型計算樣本點對應的輸電塔桿件的應力σ和結構的最大位移umax，并根據等式(8)計算優化算法中粒子的適應度函數，依據算法規則進行尋優，直至優化迭代次數達到給定的最大迭代次數，輸出結構最優設計結果{xmin、Wmin}。

4 優化設計結果分析

在考慮半剛性連接的輸電塔結構離散優化設計中，共涉及64根輸電塔主材桿件，將主材截面尺寸按不同高度、不同區域分為16組，故離散優化設計變量的個數n=16，在優化過程中每根角鋼有6種不同截面型號可供選擇，其取值如表2所示。

表2 離散變量的尺寸集合Table 2 Allowable values for the discrete design variables

1)優化過程分析

采用基于罰函數法的PSO算法對半剛性連接的輸電塔進行離散優化設計，其優化收斂曲線如圖5所示。

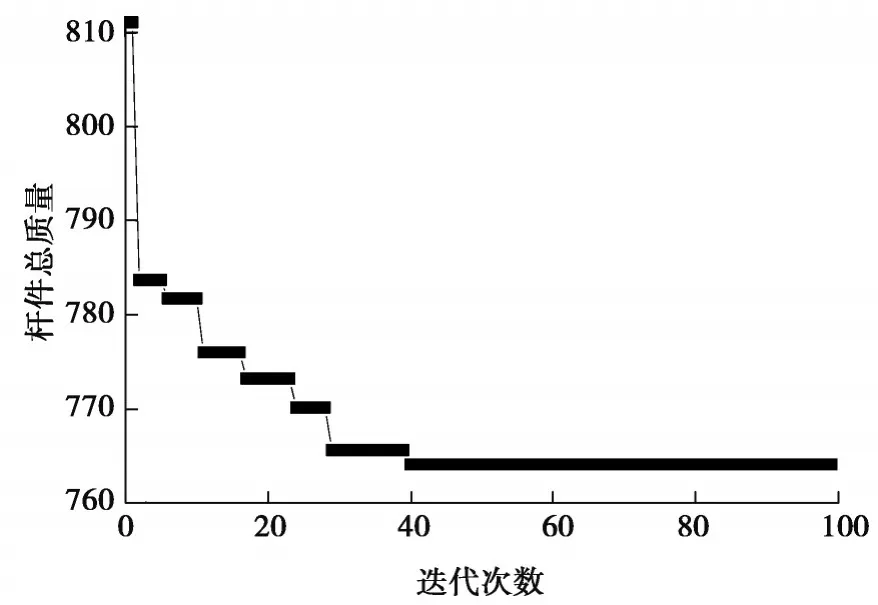
圖5 離散優化過程Fig. 5 The process of discrete optimization

圖5中展示了優化的輸電塔桿件總質量隨PSO算法迭代次數的變化趨勢，隨著優化次數的增加，構件總質量逐漸下降并最終趨于一個穩定值，在前40代，優化算法在設計空間中不斷探尋潛在最優解，收斂速度較快；在40代左右找到一個最優解，此后桿件總質量最小值不再發生變化。

2)優化前后桿件質量對比

依據方法對半剛性連接的輸電塔主材進行離散優化設計，并對優化結果進行分析。優化設計前后桿件截面尺寸發生變化的情況如表3所示。

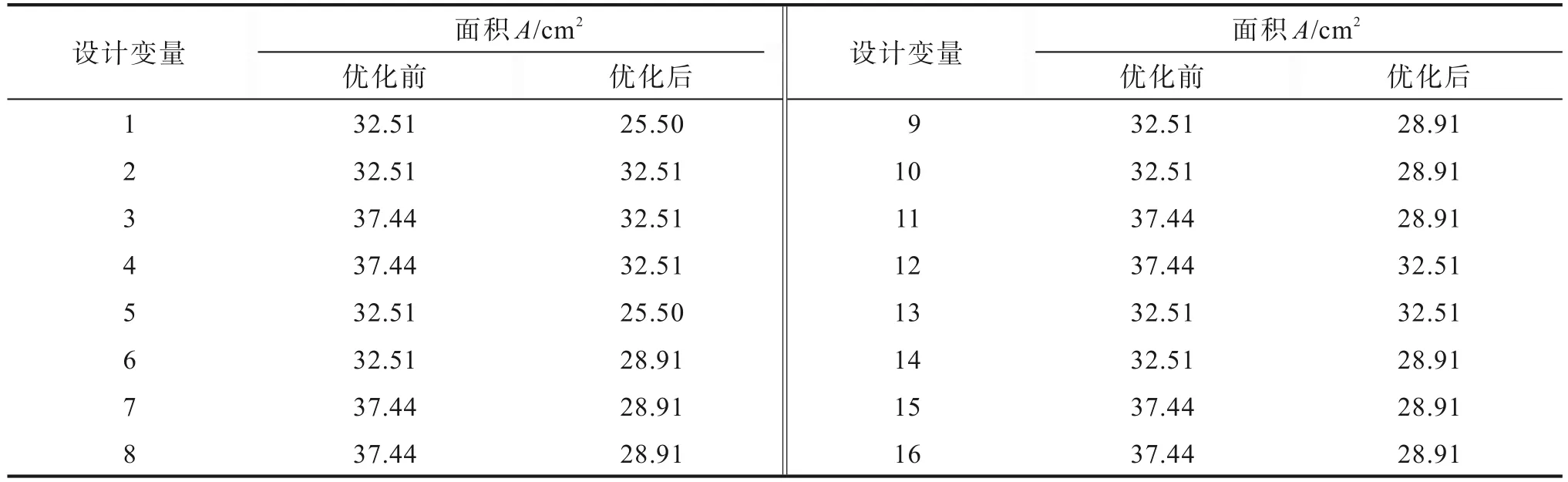
表3 優化前后截面面積對比Table 3 Comparison of section area before and after optimization

從表3可以觀察到，在優化后各桿件的截面設計發生了顯著變化，其截面面積有所下降，進一步比較優化目標函數結果，優化設計前后構件重量的對比情況見表4。

表4 優化前后總重量對比Table 4 Comparison of weight before and after optimization

由表4可知，對考慮半剛性連接的輸電塔主材進行離散優化有效降低鋼材的總質量，減少鋼材消耗量，節約經濟成本，該輸電塔離散優化設計的優化效率ξ為

3)優化前后桿件應力、位移對比

對優化設計前后考慮半剛性連接的輸電塔進行結構響應分析，輸電塔主材桿件的應力以及輸電塔結構的最大位移分別如表5和表6所示。

表6 優化前后桿件位移比較Table 6 Comparison of displacement before and after optimization

由表5可知，在離散優化設計后，輸電塔主材的應力隨著桿件橫截面面積變化發生相應變化，與優化前對比，除桿件9、44、46的應力基本不變或略有減小，其他桿件的應力均在原基礎上小幅上升，對桿件材料的利用效率更高；為保證結構具有一定的安全裕度，在應力約束條件中設置的應力容許值較小，故上述桿件應力變化幅度較小，且均未達到嚴格的滿應力狀態，在應用中設計者可根據實際要求做出相應調整。

此外，由表6可知，對輸電塔主材截面尺寸進行優化設計后，由于絕大多數截面尺寸減小，輸電塔整塔結構在X、Y、Z3個方向上的最大位移均有所上升，但影響較小，處于所給定的位移約束要求范圍內。

5 結 論

對考慮半剛性連接的輸電塔結構進行離散優化設計，主要結論如下：

1) 通過引入實際輸電塔半剛性節點的彎矩-轉角曲線，采用彈簧單元模擬半剛性節點的力學性能，建立考慮半剛性節點的輸電塔有限元模型；

2) 建立了考慮半剛性連接的輸電塔結構離散優化設計數學模型和方案，提出考慮半剛性連接的輸電塔優化設計方法；

3) 對半剛性連接的輸電塔結構進行離散優化設計，在滿足結構應力及變形約束的條件下減少了13.39%的輸電塔用鋼量，提高材料利用率，有良好的工程經濟效益。