剪力墻構件恢復力模型在OpenSees中的應用

羅國勝，顧冬生

（江南大學 環境與土木工程學院，江蘇 無錫 214122）

鋼筋混凝土剪力墻因具有較大的抗側剛度，能有效控制結構水平位移，而廣泛應用于高層與超高層建筑結構中。雖然高層結構總體抗震性能良好，但是在歷次大地震中高層結構出現嚴重損壞的案例也屢見不鮮，在2010年智利地震[1]和2011年新西蘭地震[2]中大量剪力墻出現嚴重破壞，表明對于剪力墻抗震性能還需進一步研究，特別是對于剪力墻變形能力相關的計算。大量的研究表明：數值計算已經成為高層結構抗震研究的一個有效手段，其中OpenSees (open system for earthquake engineering simulation)作為一款有限元軟件已經得到廣大研究人員的重視，其豐富的材料庫和單元庫，以及高效的算法使之成為抗震領域重要的開放科研平臺[3]。

對剪力墻受力行為的模擬可以有很多方法，在OpenSees中可以采用纖維梁柱單元來模擬，該模型能較好地考慮彎矩和軸力的耦合，但是不能直接考慮剪切變形，一般要結合另外的單元來模擬剪切變形[4]。近年來能考慮彎曲和剪切耦合作用的SFI模型（shear-flexure interaction model，SFI）得到了較多的應用[4]。國內陸新征等[5]開發了精細分層殼單元來模擬剪力墻彎剪行為，也得到了滿意的效果。總體上這幾種方法，模擬精度都比較高，但模型單元多、計算量大、計算效率較低。

對于剪力墻變形能力的計算方法已經有了較多的研究。Abdullah等[6]通過對164片剪力墻進行參數分析，提出了剪力墻位移能力的計算公式，并與剪力墻試驗結果比較，驗證了計算公式的準確性。梁興文等[7-8]通過截面分析計算了矩形剪力墻的屈服位移，提出剪力墻的4折線彎矩-曲率模型并計算了關鍵點，但提出的模型沒有考慮剪切變形，且對比的試驗數據較少，精確度有待研究。張松等[9]通過15片剪力墻擬靜力試驗提出了剪力墻三折線骨架曲線并給出了關鍵點計算方法，但擬合公式的參考數據較少，試件參數的范圍也有一定的局限性。錢稼茹等[10]通過較多的剪力墻試驗數據回歸出了屈服轉角和極限轉角的計算公式。李宏男等[11]提出了RC剪力墻的多彈簧宏觀計算模型，并通過9片剪力墻試驗驗證了模型的正確性。

在上述相關研究的基礎上，筆者提出剪力墻構件的恢復力模型，骨架曲線用彎矩-轉角三折線模型來定義。收集了105片剪力墻試驗數據，提出了考慮剪跨比影響的有效剛度計算公式，研究了受彎承載力最大值計算方法，對現有的剪力墻變形能力計算模型進行評估，對于承載力和剛度退化行為，采用OpenSees中成熟ModIMK滯回規則進行模擬。提出的恢復力模型可以直接用于模擬剪力墻從彈性到彈塑性，以及最后進入軟化段全過程的非線性變形行為。與精細的SFI模型和分層殼模型進行比較表明，文中提出的模型有足夠的精度，計算效率高收斂性好，并通過增量動力分析(incremental dynamic analysis, IDA)來進一步驗證該模型的有效性。

1 恢復力模型骨架曲線

1.1 三折線骨架曲線

剪力墻在側向荷載作用隨著側向荷載的增加，墻體經歷混凝土開裂和鋼筋屈服等過程，側向荷載達到最大值后逐步下降，墻體發生破壞。這一過程可以簡化為三折線模型，如圖1所示，分為屈服段、強化段和軟化段。受拉區最外側混凝土開裂前，剪力墻處于彈性階段，當側向位移角達到θ′y時，剪力墻首次屈服，M′y為首次屈服彎矩，定義為最外側混凝土壓應變達到0.002或者最外側受拉鋼筋屈服時彎矩的較小值[12]。當軸壓較小時一般鋼筋受拉屈服先于混凝土受壓屈服。My為屈服彎矩，取最外側混凝土壓應變達到0.004時的截面彎矩[12-13]。構件達到屈服彎矩后，一般受彎承載力會有一定上升，其最大值Mc為峰值彎矩，峰值位移角為θc。

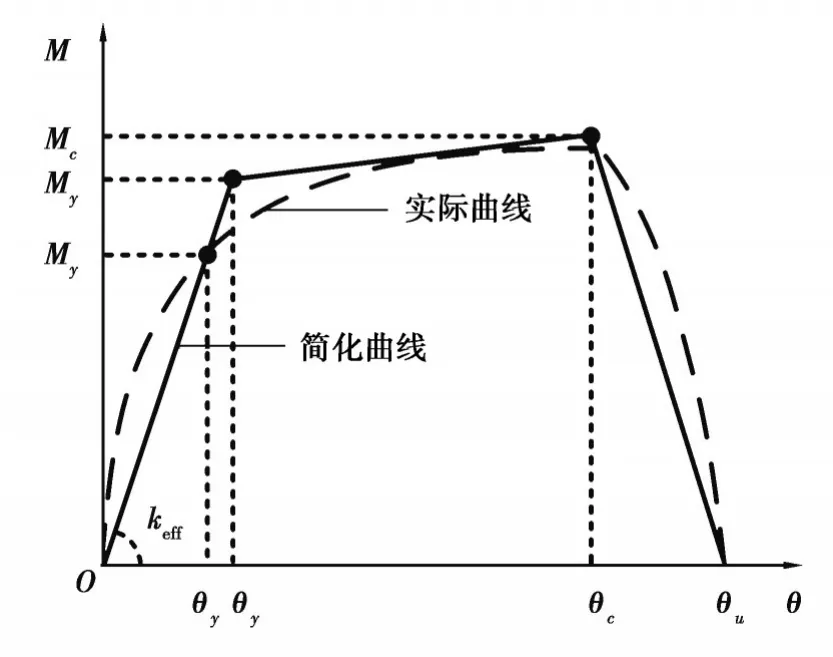
圖1 剪力墻彎矩-轉角骨架曲線Fig. 1 Moment-Angle skeleton curve of shear wall

1.2 彈性段定義

側向位移位移角可以表示為屈服位移角θy和塑性位移角θp之和

對于懸臂剪力墻彎曲變形，根據彈性理論

式中：EcIeff為截面有效剛度；heff為剪力墻高度。鋼筋混凝土剪力墻側向位移主要由彎曲、剪切、底部鋼筋從基礎中滑移引起的側向變形3部分組成，滑移變形一般相對較小，不足10%。當剪力墻剪跨比較小時，剪切變形不能忽略，試驗表明剪跨比低于1.0時剪力墻的剪切變形能達到總變形的50%左右，所以要通過試驗結果研究剪跨比對截面有效剛度的影響。

2 截面有效剛度計算

2.1 現有的計算模型

當剪力墻剪跨比變小時，剪切變形占比會逐漸增加，可以通過減小式(3)截面有效剛度來考慮剪切變形的影響。Paulay等[14]通過試驗研究與數值分析提出了考慮剪切變形的剪力墻截面有效剛度計算公式

式中：EcIg為剪力墻毛截面剛度；fy為縱筋屈服強度；lw和bw分別為剪力墻截面的長和寬；n為軸壓比；F為

由式(4)和式(5)可以看出隨剪跨比heff/lw增大，F減小，從而截面有效剛度增大。當fy取400 MPa，n=0.1時，heff/lw從1.5增加到3，EcIeff/EcIg從0.22增加到0.27。

Li等[15]在Paulay等[14]研究基礎上對剪跨比小于2.0的試件進一步研究，提出了截面有效剛度的建議公式，為

同樣的heff/lw從1.5增加到3，EcIeff/EcIg從0.12增加到0.29。可以看出在剪跨比較小時，式(6)計算結果顯著小于式(4)。

Haselton等[16]對鋼筋混凝土柱試驗結果研究認為截面有效剛度只與軸壓比n和剪跨比heff/lw有關，并在大量試驗數據基礎上提出

2.2 截面有效剛度試驗結果

為了驗證截面有效剛度計算方法，筆者對國內外試驗結果進行總結。選擇矩形截面兩端有約束邊緣的試件，端部約束區箍筋間距不超過100 mm，箍筋間距與縱筋直徑比值不超過10，以保證塑性變形區有較好的約束。共收集了105片剪力墻試驗結果，剪跨比范圍為1.0~6.0，軸壓比范圍為0~0.51，基本涵蓋了剪力墻工程參數常用范圍。對于每個試件，用OpenSees建立剪力墻的纖維模型，通過截面分析，提取墻截面最外側混凝土壓應變達到0.004時的截面彎矩作為屈服彎矩理論值My；根據試驗屈服位移，通過式(3)計算截面有效剛度試驗值。剪力墻基本信息和計算結果見表1所示。根據公式(4)、(6)和(7)計算截面有效剛度，圖2給出了有效剛度計算值和試驗值的比與剪跨比的關系。

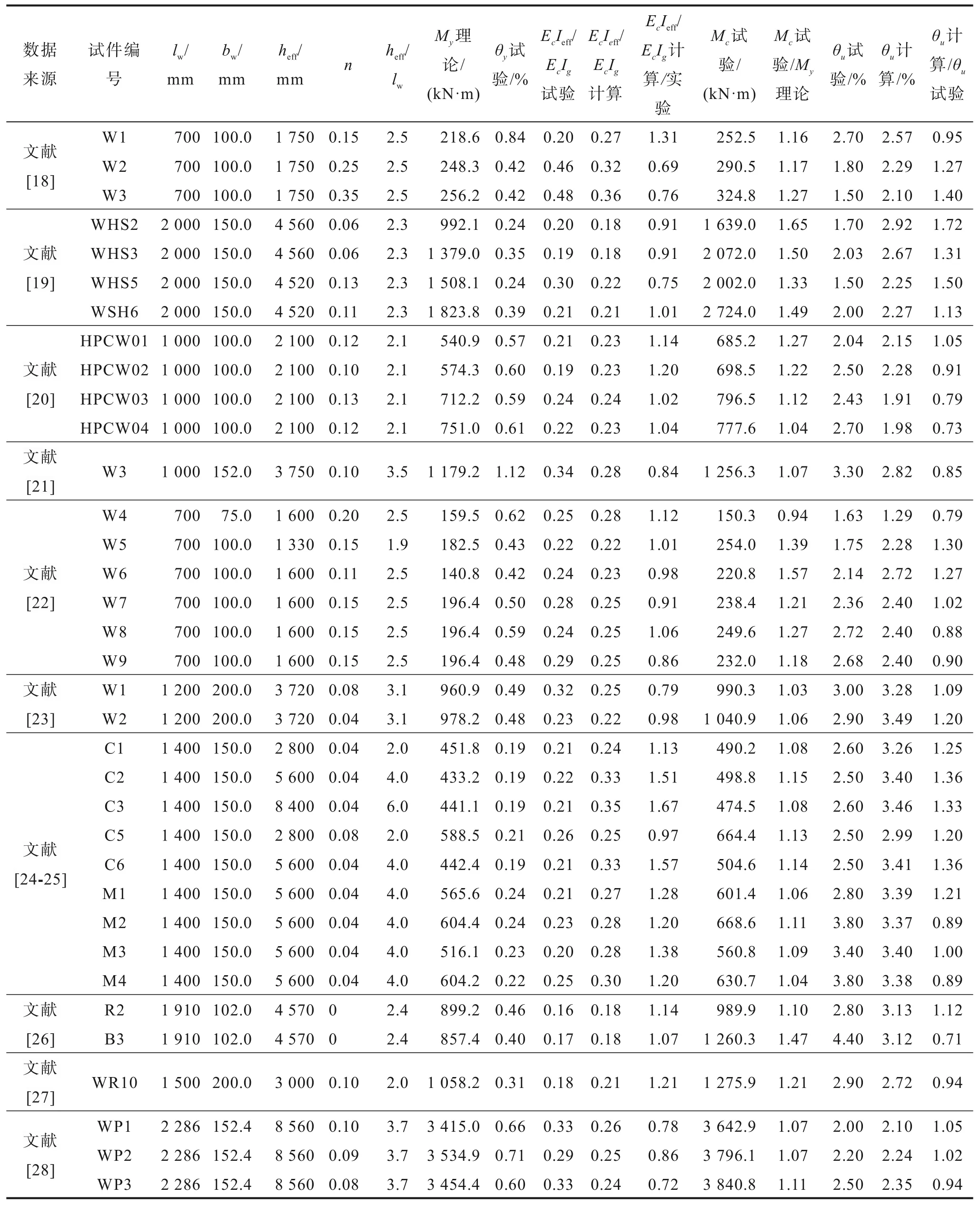
表1 試驗數據與計算結果Table 1 Test data and calculation results

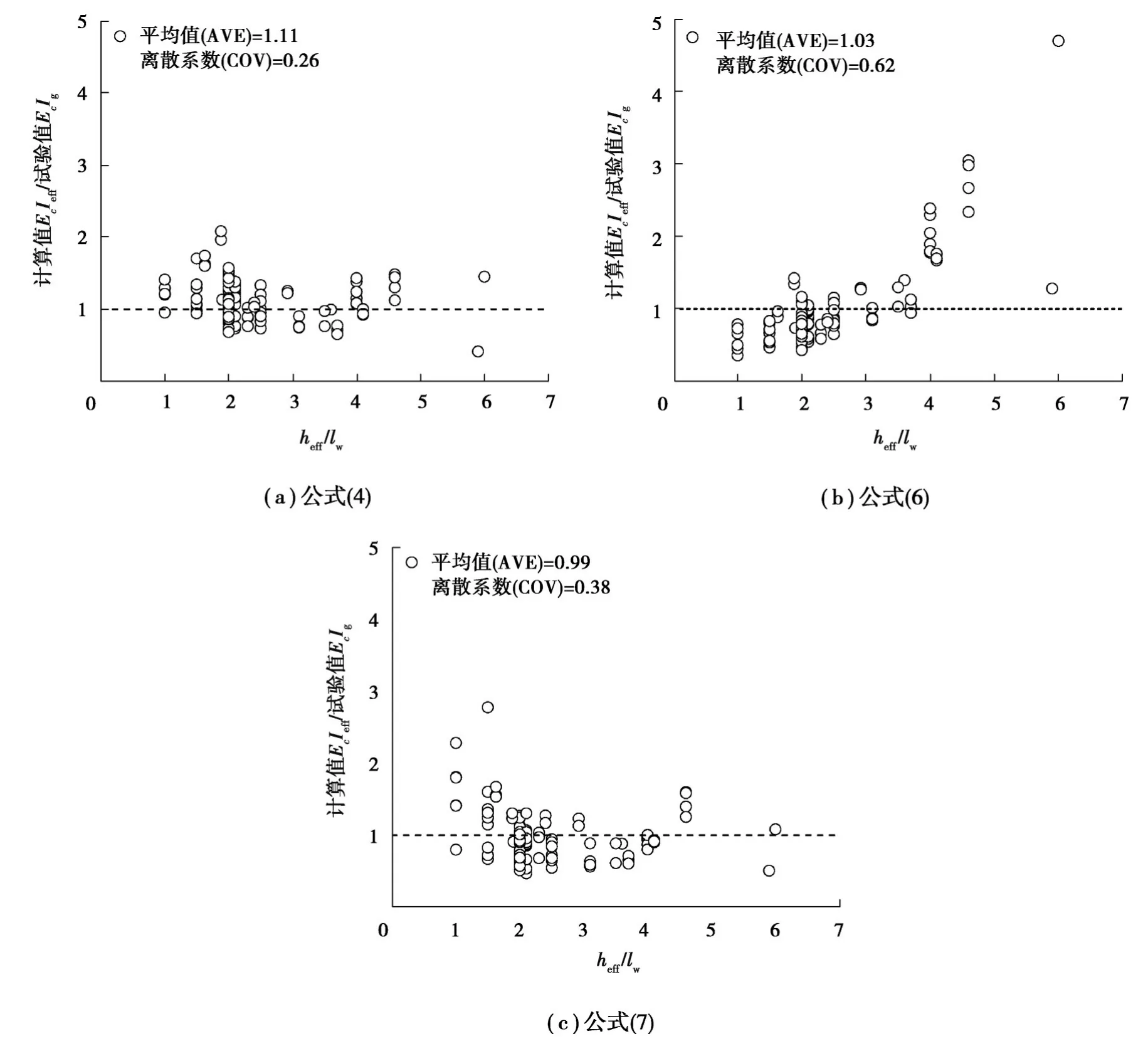
圖2 有效剛度計算結果與剪跨比的關系Fig. 2 Relationship between effective stiffness calculation results and shear span ratio

式(6)是通過低剪跨比的試驗結果回歸出來的，適用于低剪跨比的截面有效剛度計算，其計算值與實驗值比的平均值為1.03，離散系數為0.62。heff/lw在2.0~6.0范圍內式(4)和式(7)的計算結果與試驗值吻合較好，但在heff/lw小于2.0時誤差相對較大，計算結果都偏大的比較多。從圖2結果可以看出總體上式(4)的計算結果精度最好，筆者對式(4)進行了系數調整：

圖3給出了文中建議的式(8)計算結果與剪跨比的關系，在剪跨比小時計算精度有所提升，截面有效剛度計算值與試驗值比值的均值1.04，離散系數0.26，說明調整后的計算公式可以較為準確地預測截面有效剛度。

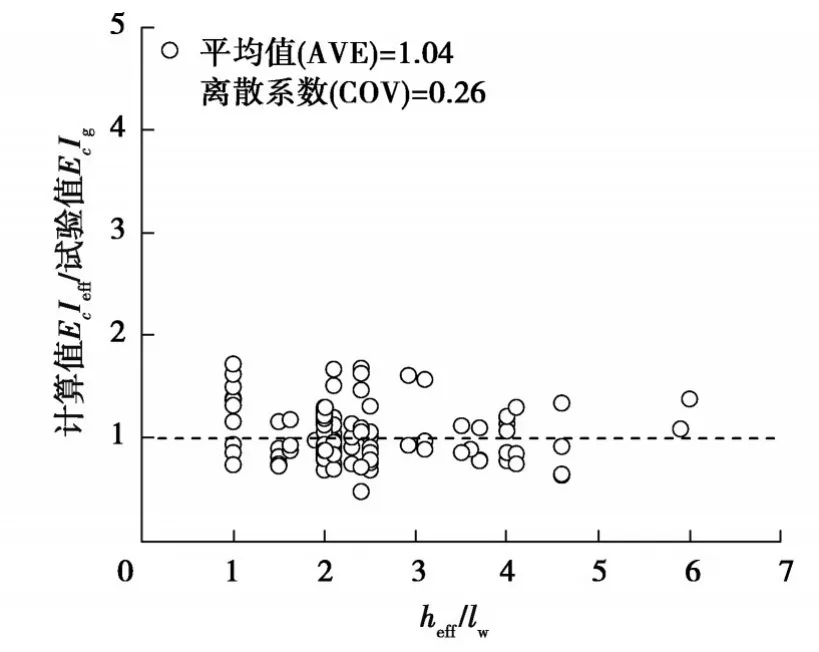
圖3 式(8)計算結果與剪跨比的關系Fig. 3 Relationship between the calculation results of equation 8 and shear span ratio

對于截面屈服彎矩My，文中用的是OpenSees計算的值，也可以根據Panagiotakos等[17]提出的公式進行計算。文中也對這2種計算結果進行了比較，根據統計，公式計算值與程序計算值比值的平均值為1.0，離散系數為0.13，說明文獻[17]提出的方法計算結果精度很高，可以用于計算屈服彎矩。

3 強化段定義

3.1 峰值彎矩確定

剪力墻進入塑性階段后，隨著位移增加，受彎承載力會有所增大，這是由于鋼筋進入強化階段以及混凝土受到箍筋約束共同作用的結果，承載力達到峰值之后開始進入下降段，直到剪力墻破壞。根據文獻[42]對于RC柱受彎承載力的研究，峰值彎矩Mc為

計算了收集的105片剪力墻的峰值彎矩，并與實驗值對比，計算值與實驗值比值的平均值為1.11，離散系數為0.17，計算結果相對偏大。圖4給出了105個試件Mc試驗值與My理論值的比值與軸壓比的關系，可以看出軸壓增加對彎矩的增長效果并不顯著，主要是剪力墻的軸壓比一般較小，絕大部分在0~0.3之間，所以影響較小。從圖4可以看出，Mc/My均值為1.10，離散系數為0.17，離散較小。峰值彎矩Mc可由式(10)進行簡化計算，對于RC柱，文獻[42]建議這一比值為1.13。

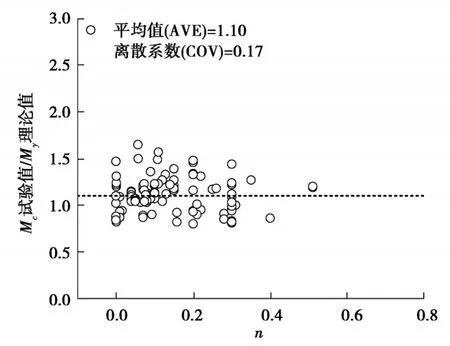
圖4 彎矩增強系數與軸壓的關系Fig. 4 Relationship between moment enhancement factor and axial pressure ratio

3.2 峰值轉角的計算

剪力墻變形達到一定值時，底部塑性區的破壞逐漸嚴重，受壓區約束混凝土出現壓碎，局部鋼筋出現屈曲，承載力迅速下降，構件發生破壞。對于峰值變形能力主要與軸壓比和約束區箍筋用量有關[9]。近年來Abdullah等[6]經過大量大尺寸試驗研究發現，當約束箍筋滿足一定要求時，峰值變形能力主要與受壓區高度和截面的長寬比（lw/bw）相關，箍筋的用量不會影響變形能力，隨著截面寬度增加，峰值變形能力能有較大增加。這也和大量剪力墻震害現象吻合，截面寬度小時，剪力墻破壞特別嚴重[2]。文獻[6]在試驗研究基礎上提出了峰值位移的計算公式

式中：vmax為最大剪應力，通過峰值彎矩計算值計算；c為最外側混凝土應變0.004時受壓區高度。受壓區高度一般與軸壓比和縱筋配筋率有關。文獻[43]提供了的63片矩形剪力墻混凝土應變達到0.004時的受壓區高度，根據這些數據進行回歸分析，提出

式中：kf為腹板縱筋配筋特征值，kf=ρwfyw/fc計算，式中ρw為腹板縱筋配筋率，fyw為腹板縱筋屈服強度。

計算結果與文獻[43]的數據對比見圖5所示，計算值與對比數據的比值平均值為1.04，離散系數為0.24，可以看出計算結果較好，說明式(11)可以比較準確地計算剪力墻受壓區高度。

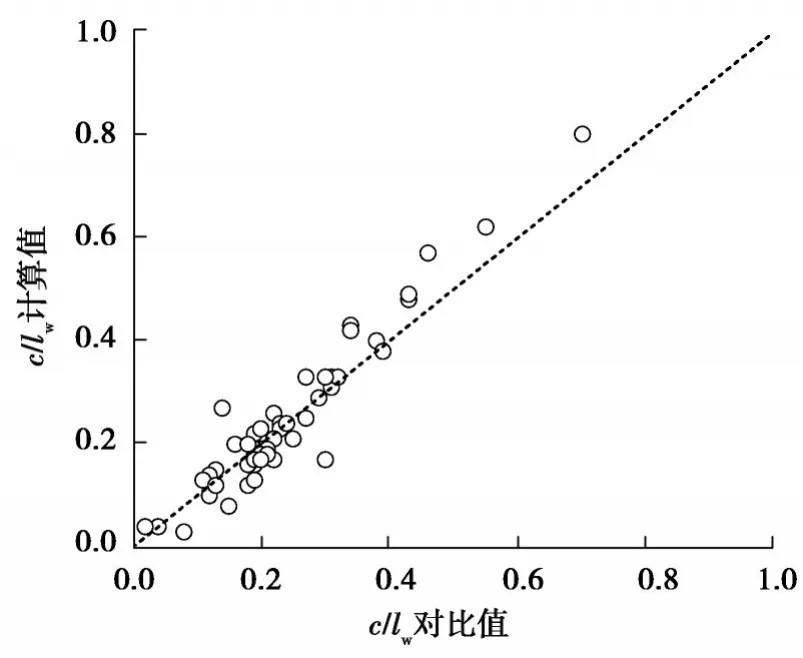
圖5 式(11)計算結果Fig. 5 Calculation results of equation 11

用式(11)計算文中收集的105片剪力墻峰值轉角，受壓區高度由式(12)計算，計算值和試驗值的比值與約束區箍筋的配箍特征值關系見圖6所示，比值平均值為1.03，離散系數為0.29，計算結果離散性較小。

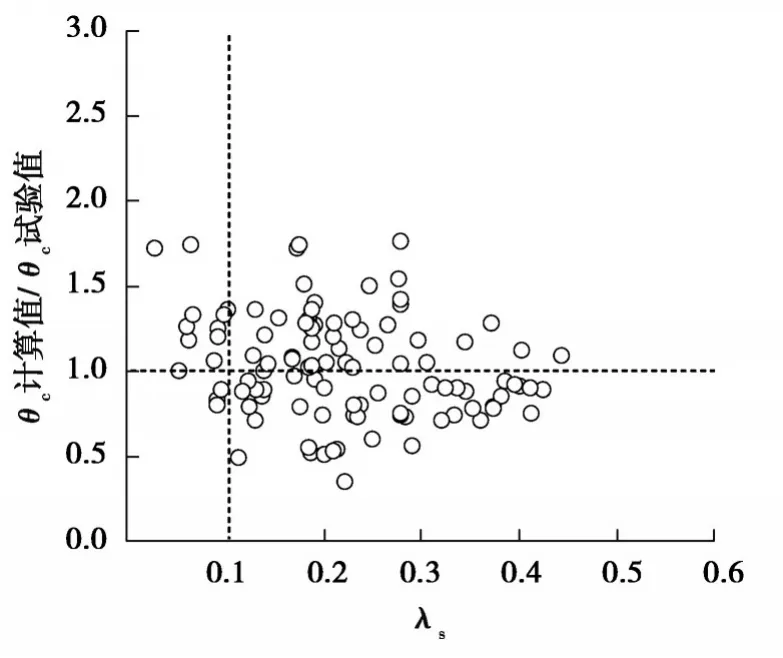
圖6 峰值轉角計算精度與配箍特征值關系Fig. 6 Relationship between the peak rotation

從圖6 可以看出對于配箍特征值小于0.1的13個試件，計算值大于和等于試驗值的試件數量有11個，說明在箍筋用量較小時，式(11)的計算結果偏大。當配箍特征值大于0.1時，計算值與試驗值比值大于1的試件數量并不明顯多于小于1的試件數量，說明不考慮箍筋用量不會顯著影響計算精度。圖6統計結果表明在箍筋用量較少時，增加箍筋用量對變形能力是有利的，這和文獻[10-11]結論吻合，當箍筋用量達到一定量時再增加，就不能顯著增加剪力墻的變形能力；另外，文獻[44]通過對端部有約束箍筋的剪力墻試驗進行分析也得到了類似結論，并建立有限元模型進行了驗證。這一現象的主要原因是隨著箍筋用量的增加，剪力墻的破壞從混凝土受壓破壞轉變為縱筋屈曲受拉斷裂破壞為主，而當箍筋間距滿足一定要求時，箍筋用量的進一步增加并不能顯著增加縱筋的抗屈曲斷裂的能力。根據這些討論，說明式(11)適用于箍筋用量較多的試件，在應用時要予以注意。

4 數值模擬

4.1 低周反復模擬

4.1.1 滯回規則確定

選擇OpenSees中的可以考慮強度與剛度退化的ModIMK材料來定義剪力墻的滯回規則，如圖7所示，剪力墻的骨架曲線關鍵點用文中提出的計算方法計算。剪力墻在往復加載下耗能增加，會出現強度和剛度退化[45]，在ModIMK材料中可以通過4個退化系數來控制，分別是屈服強度退化系數、峰值后強度退化系數、卸載剛度退化系數和再加載剛度退化系數。

退化由能量耗散能力Et控制，根據Haselton等[42]，能量耗散能力Et由屈服彎矩My和峰值轉角θc計算，計算公式為：

式中，λ為能量耗散系數，Haselton等[42]建議λ=30(0.3)n。ModIMK材料中4個退化系數可取相同值[42]，其表達式為30(0.3)nθc。由于剪力墻變形能力相對于RC柱明顯偏小，其強度和剛度的退化并不明顯。

根據文獻[45]，骨架曲線過了峰值點進入下降段的剛度kc=αckeff。對于RC柱，αc根據約束箍筋情況取-0.1~-0.5；對于剪力墻，承載力進入下降段一般破壞比較迅速，這里建議取-1，由此可以計算最終破壞時的轉角大小。

4.1.2 滯回模型應用

應用文中提出的滯回模型，采用OpenSees對剪力墻試驗進行了模擬，這里給出了文獻[29]中的C10剪力墻模擬結果。剪力墻試件部分參數見表1，保護層厚度為27 mm，混凝土強度32.7 MPa；邊緣約束區配有20根直徑為16 mm的縱筋，屈服強度為543 MPa；約束箍筋直徑為6 mm，箍筋間距65 mm；腹板區長1 430 mm，共配20根直徑10 mm縱筋，屈服強度為507 MPa。圖8給出了剪力墻對稱截面配筋信息。

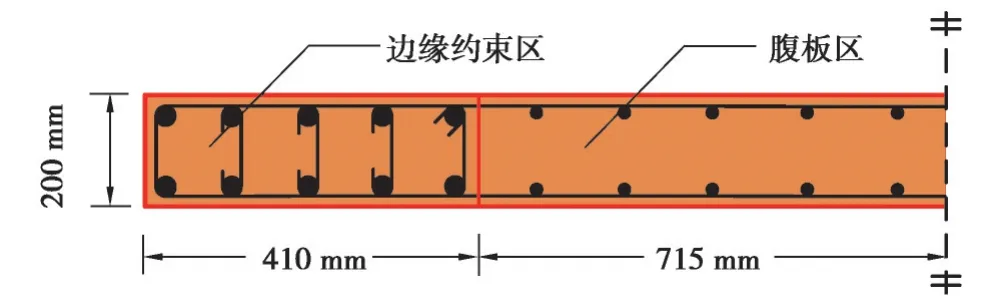
圖8 C10剪力墻截面Fig. 8 Shear wall section of C10

剪力墻的ModIMK分析模型如圖9所示，OpenSees建模時，剪力墻采用彈性單元(elasticBeamColumn element)模擬，底部設零長度單元(zeroLength element)，通過ModIMK材料來定義零長度單元轉動關系來模擬剪力墻變形，其材料本構關鍵點采用文中提出的計算方法計算。表2列出了C10關鍵點計算結果，可以看出計算結果精度較高，說明文中提出的三折線計算模型能有效預測剪力墻的受力行為。

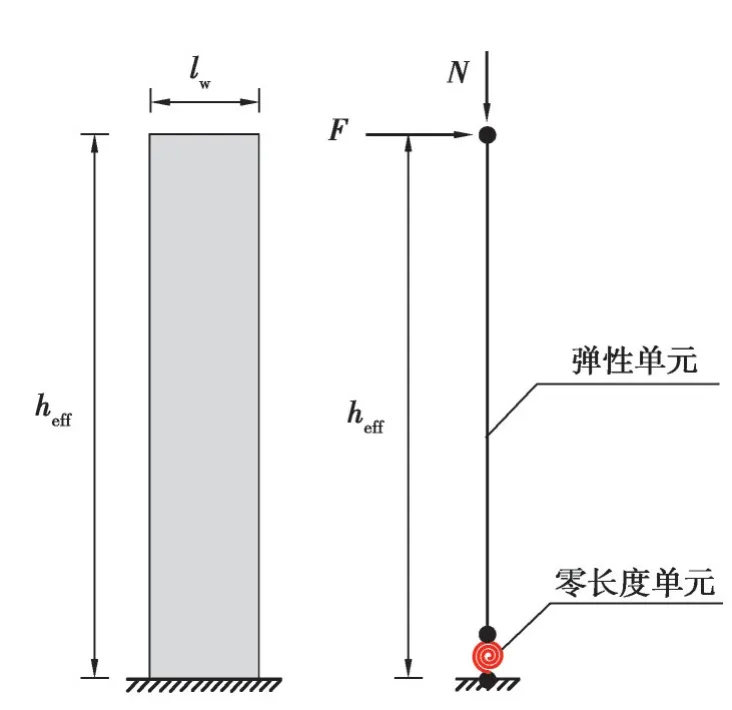
圖9 C10剪力墻ModIMK模型Fig. 9 Shear wall ModIMK model of C10

圖10為剪力墻數值模擬結果和試驗結果對比，從圖中可以看出兩者曲線吻合較好，強度、剛度退化也能很好模擬。計算的峰值位移點和試驗結果比較接近，在加載負方向，計算結果很好地模擬了破壞過程。

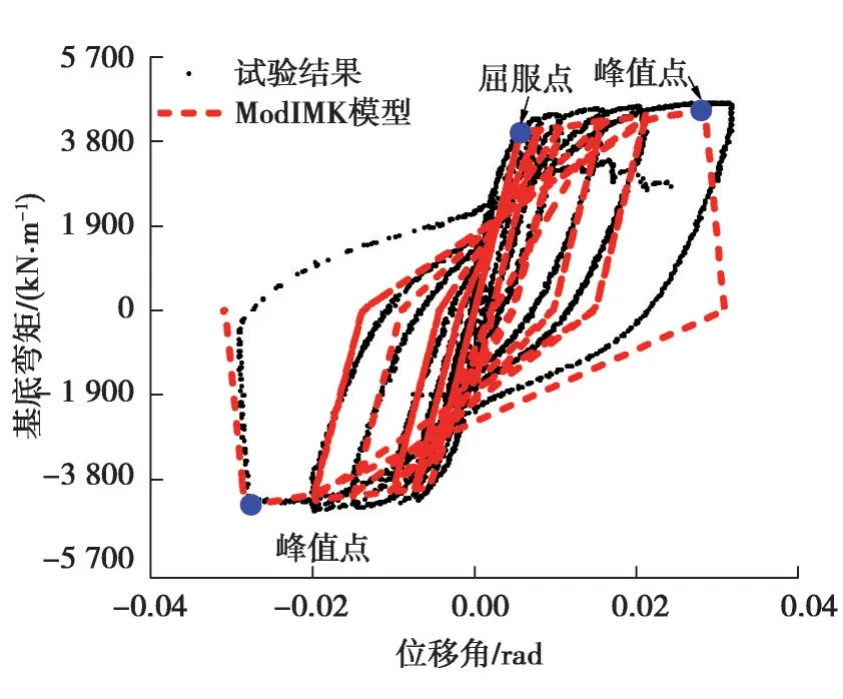
圖10 C10 ModIMK模型模擬結果Fig. 10 ModIMK model simulation result of C10

4.1.3 與分層殼模型對比

文獻[5]開發的基于OpenSees平臺的分層殼單元可以很好地模擬剪力墻受力過程，在應用時，腹板區和邊緣約束區分別由不同層數的鋼筋和混凝土材料層組成，通過定義每一層鋼筋或混凝土本構來計算單元的應力和應變。謝琳琳等[46]用這一單元對文獻[41]中試件SW1-1進行了模擬，剪力墻高2 000 mm，墻截面長為1 000 mm，寬125mm；混凝土強度為20 MPa，剪力墻軸壓比為0.1；單測邊緣約束區長200 mm，配有6根直徑為10 mm的縱筋，屈服強度為352 MPa，約束箍筋直徑為6 mm，箍筋間距為80 mm，屈服強度為392 MPa；腹板區配10根直徑為6 mm的縱筋。

建立剪力墻的ModIMK模型，建模方法與上文一致。低周反復模擬結果如圖11(a)所示，按2個方向骨架曲線平均值計算，屈服位移試驗值為6.4 mm，模擬結果為5.3 mm，比試驗值小17%，峰值剪力分別為195 kN和183 kN，誤差只有6%，可以看出ModIMK模型屈服點、峰值點和破壞段都與試驗結果吻合很好，特別是負方向過了峰值點的下降段很準確地模擬了試驗破壞過程。

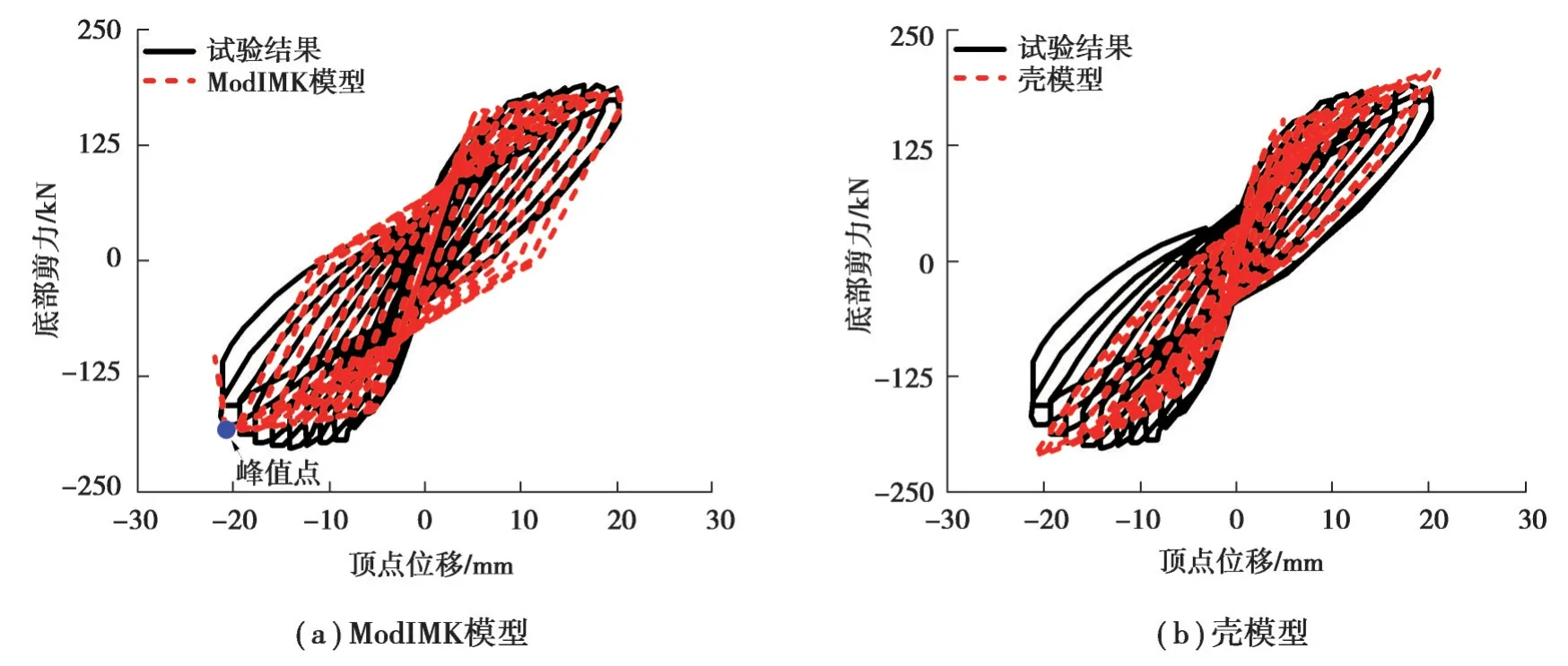
圖11 SW1-1試驗和模擬結果對比Fig. 11 Comparison of SW1-1 test and simulation results

殼模型模擬結果如圖11(b)所示，可以看出殼模型可以精確模擬剪力墻的剛度和承載力，特別是卸載段剛度吻合很好，但達到峰值后沒有承載力沒有下降趨勢，對于破壞和下降段的模擬似乎值得進一步探討。

4.2 時程分析模擬

為驗證文中的剪力墻滯回模型在地震作用下的適用性，選擇文獻[4]中的5層框架剪力墻進行時程分析模擬。剪力墻每層高3 660 mm，長6 100 mm，厚度為305 mm，一側邊緣約束區配16根直徑為36 mm的縱筋，屈服強度為410 MPa，箍筋直徑為13 mm，間距為102 mm；混凝土強度為34 MPa；框架跨距為6 100 mm，框架柱為710 mm×710 mm的矩形柱，梁尺寸為460 mm×810 mm。

框架剪力墻的ModIMK模型如圖12所示，由于除頂層外每一層剪力墻上下兩端都存在彎矩，都有可能進入塑性，需在兩端各設一個轉動彈簧以模擬其轉動，并賦予相同的ModIMK材料本構。需要注意的是，上下兩端都設彈簧的情況下，式(3)中系數3應為6，建模時線剛度采用一半層高計算。對于框架梁柱，采用文獻[4]中建模方法，框架梁柱采用彈性單元模擬，梁柱結點和支座處的塑性鉸區設轉動彈簧以模擬其轉動，彈簧采用ModIMK材料定義。剪力墻與框架之間采用剛性連接，控制每層框架和剪力墻的水平位移相等。

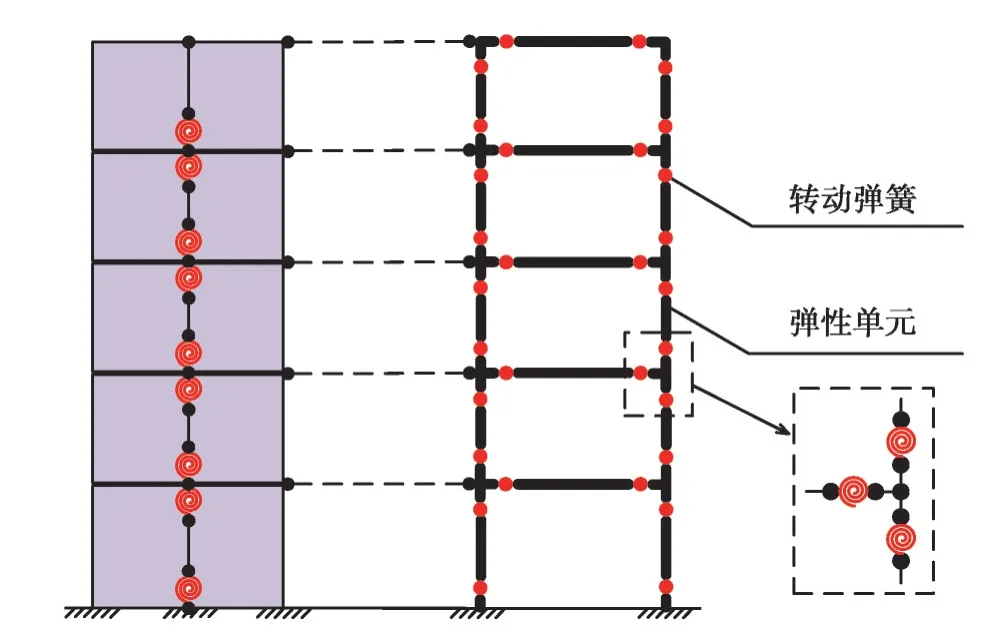
圖12 5層框架剪力墻ModIMK模型Fig. 12 5 storey frame-shear wall ModIMK model

文獻[4]采用OpenSees中的彎剪耦合多連桿模型SFI-MVLEM單元模擬剪力墻，框架部分的建模與上文一致。每層剪力墻由2個相同的SFI_MVLEM單元模擬，混凝土采用ConcreteCM材料，Steel02材料模擬鋼筋，把鋼筋和混凝土賦予FSAM材料定義剪力墻纖維板，并對每個SFI-MVLEM單元設6個纖維板定義剪力墻單元[47]。

SFI-MVLEM和ModIMK模型采用倒三角形加載方式Pushover的結果見圖13所示，可以看出2種模型的屈服段比較吻合。SFI-MVLEM隨著側向位移的增加，底部剪力逐漸增加，頂部位移達到1 100 mm時進入下降段，此時頂點位移角達6.1%，這一位移角明顯高估了剪力墻的變形能力。ModIMK模型剪力墻發生破壞時的峰值位移為430 mm，轉角為2.4%，分析結果更合理，圖中剪力墻破壞之后底部剪力還有一定值是因為框架還沒破壞。

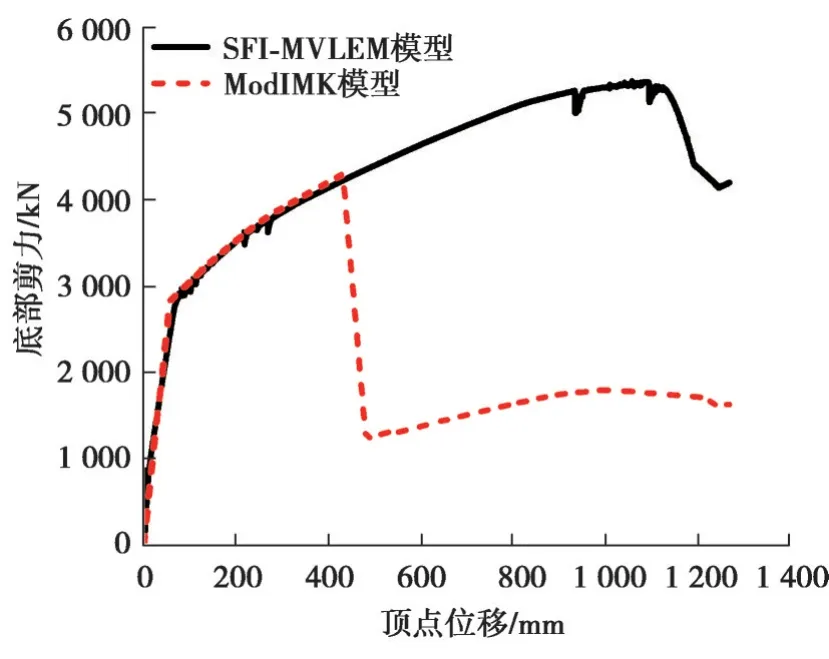
圖13 Pushover分析對比Fig. 13 Pushover analysis

文獻[4]還用SFI-MVLEM模型進行了時程分析模擬，結果如圖14所示，采用同一條波對文中的ModIMK模型進行分析，從圖中可以看出2種模型時程分析結果基本吻合，說明ModIMK模型可以和精細有限元一樣有效預測框架剪力墻在地震作用下的響應。

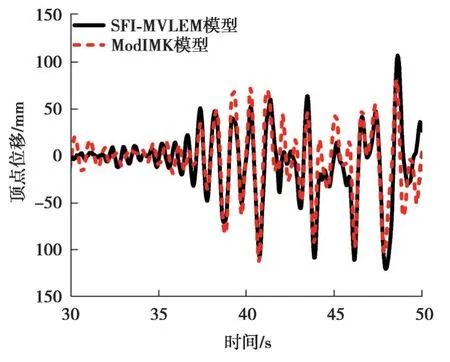
圖14 時程分析對比Fig. 14 Time history analysis

4.3 IDA計算

增量動力分析(IDA)可以預測結構在地震作用下的倒塌概率，在太平洋地震工程研究中心(PEER)地震波數據庫中下載了13條遠場地震波，對文獻[48]的8層剪力墻進行增量動力分析，地震波信息見表3所示。剪力墻首層高4 000 mm，其余層高3 600 mm，剪力墻截面長7 000 mm，厚度500 mm，保護層厚度為59 mm，混凝土強度fc=38.8 MPa。兩端約束加強區共配32根直徑為12.5 mm的縱筋，中間腹板區配有30根直徑10 mm的縱筋，縱筋屈服強度fy=567.3 MPa；約束加強區箍筋間距為100 mm，直徑為10 mm，屈服強度fv=300 MPa。

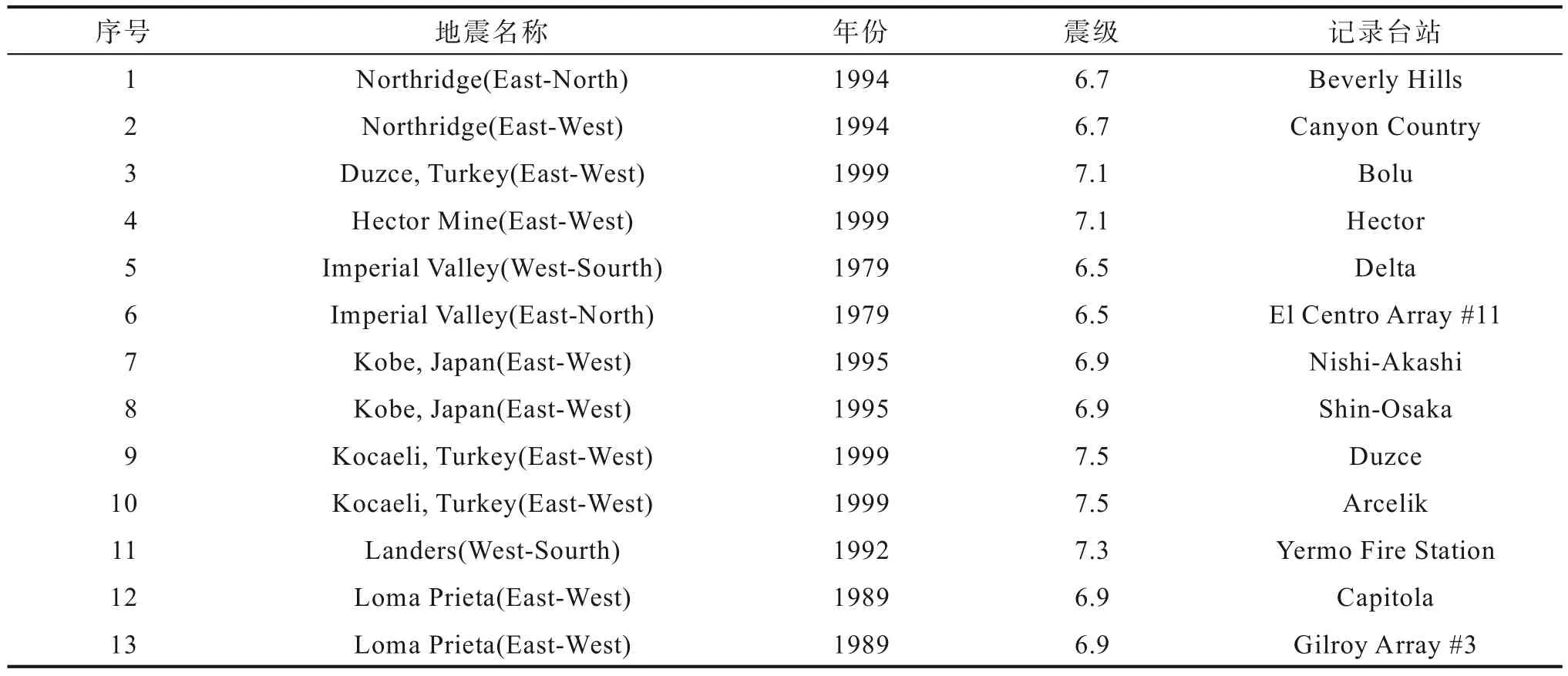
表3 13條遠場地震波Table 3 13 far-field seismic waves

文獻[48]用纖維模型進行了模擬計算，纖維模型鋼筋材料采用Steel02模擬，并用Minmax材料包裹來控制鋼筋的受壓和受拉極限應變，以此定義剪力墻的破壞準則。結構第一周期T1為0.95 s，阻尼比為5%，根據文獻[49]，以結構第一周期對應的地震譜加速度Sa(T1,5%)作為地震強度指標IM，以最大層間位移角θmax作為地震響應指標DM，文中分析時IM按0.2g的間隔增加。

圖15為2種模型的IDA結果，分析不收斂導致結構變形趨向無限大作為達到倒塌狀態。文獻[50]建議以5%的位移角作為剪力墻的上限倒塌指標，計算中最大位移角超過5%時，即便計算還能收斂也應視為結構倒塌，因為剪力墻變形位移角基本很難達到5%。圖15給出了確定Sa下對應的最大層間位移角的中值曲線(50%分位曲線)。從分析結果對比可以看出2種模型在低IM下DM指標比較吻合，在較高IM下ModIMK模型倒塌點基本在5%左側，且倒塌位移角均值接近剪力墻的極限轉角0.033。纖維模型倒塌點的最大位移角相對較大，中值曲線也驗證了這一點，原因主要是纖維模型對于破壞狀態的模擬比較復雜，其應變限值受較多的因素影響[50]。

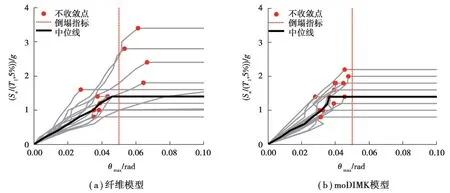
圖15 IDA結果Fig. 15 IDA results

在計算過程中ModIMK模型計算收斂性較好、計算速度快，所用的時間大約為精細模型和纖維模型的百分之一左右。

5 結 論

筆者在試驗結果和理論分析的基礎上，提出了基于ModIMK滯回規則的RC剪力墻彎矩-轉角三折線計算模型，通過數值模擬對模型進行驗證。

1）通過理論分析與試驗總結把剪力墻側向變形過程分為3段：屈服段、強化段、破壞段，提出了剪力墻的彎矩-轉角三折線模型，模型計算簡單，便于實際應用。

2）提出了模型關鍵點計算方法，通過105個試件試驗結果分析提出了截面有效剛計算方法，通過對3種計算方法對比發現剪跨比對有效剛度影響明顯，尤其在剪跨比小于2.0時有效剛度計算誤差稍大，通過對試驗數據重新擬合，文中提出的計算方法精度較高。對構件的峰值位移計算進行了研究，當箍筋間距滿足一要求時，箍筋用量達到一定量時再增加不能顯著增加剪力墻的變形能力。105個剪力墻試件的計算與試驗對比結果表明提出的彎矩-轉角三折線模型能有效預測剪力墻的非線性變形行為。

3）采用OpenSees中的ModIMK材料定義模型的滯回規則，對剪力墻低周反復試驗進行模擬，結果表明剪力墻的ModIMK模型與試驗結果吻合很好，驗證了模型的準確性；與分層殼模型的對比表明提出模型對剪力墻破壞段的模擬更有優勢。5層框架剪力墻的時程分析表明ModIMK模型能有效模擬框架剪力墻在地震作用下的響應。8層剪力墻的增量動力分析(IDA)對比表明ModIMK模型預測的剪力墻倒塌位移角比纖維模型小。