平面向量中的情境題賞析
王生云
(青海省海東市互助縣第一中學)
?普通高中數學課程標準(2017 年版2020 年修訂)?提出,選取恰當的問題情境是考查數學學科核心素養的重要載體.情境是高考數學命題的三大要素之一,情境是多樣的、多層次的,包括社會熱點、數學文化、現實生活、科學情境等.情境題是基于數學學科核心素養導向的命題,是為“問題”服務的,應以情境為命題背景,靈活進行設問,但需要注意情境背景與問題的融合.試題以考查知識、能力為基礎,通過數學情境、社會情境或科學情境提出問題,進而綜合考查學生的數學學科核心素養.筆者結合平面向量中的情境題來進行分析.
1 緊跟社會熱點
例1 圖1是2022年北京冬奧會會徽的圖案,奧運五環的大小和間距如圖2 所示.若圓的半徑均為12,相鄰圓圓心水平距離為26,兩排圓圓心垂直距離為11.設五個圓的圓心分別為O1,O2,O3,O4,O5,則=( ).

圖1

圖2
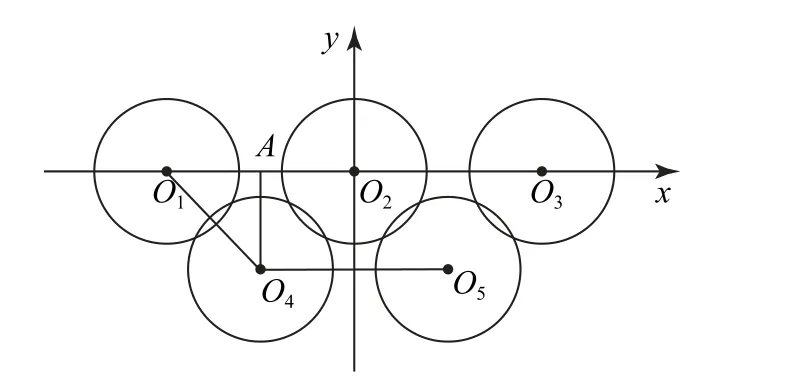
圖3
A.-507 B.-386
C.-338 D.-242


本題以社會熱點事件中某一個圖標為背景,結合平面向量的數量積來命制試題.背景材料的選取恰好符合平面向量的要求,是一道難得的好題.此類問題需要在理解情境的基礎上,尋找合適的數學模型解決.這樣的試題在高考和平常的模擬考試中出現的頻率越來越高,同時對學生的要求也越來越高,學生不僅要掌握數學的基本知識和基本技能,還需要理解問題的本質,從情境中抽離出數學問題.
2 滲透數學文化
例2 “趙爽弦圖”是數形結合思想的體現,是中國古代數學的圖騰,還被用作第24屆國際數學家大會的會徽.如 圖4 所 示,大 正 方 形ABCD由4 個全等的直角三角形和中間的小正方形組成,若,E為BF的中點,則=( ).
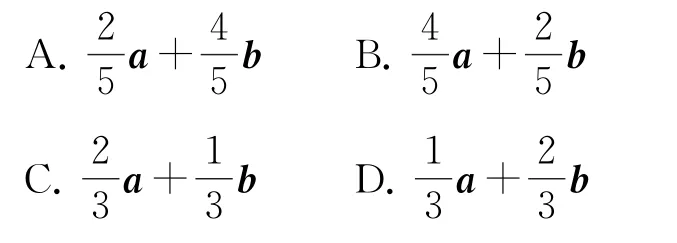

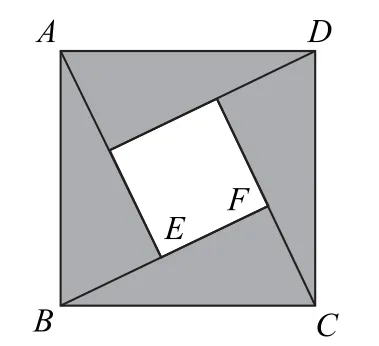
圖4
以A為原點建立平面直角坐標系,如圖5所示.不妨設AB=1,BE=x,則AE=2x,所 以x2+4x2=1,解 得.設∠BAE=θ,則,所以
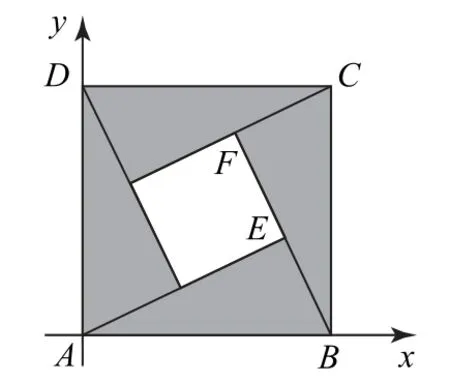
圖5
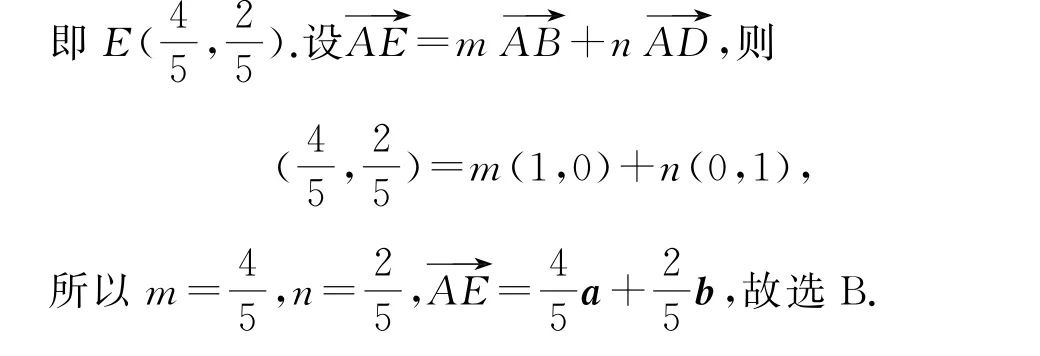

本題以學生熟知的“趙爽弦圖”為背景立意試題,考查平面向量的基礎知識及學生對基本問題的處理能力.
3 現實生活情境
例3 (多選題)圖6是一款家居裝飾物——博古架,博古架是類似于書架式的木器,其每層形狀不規則,前后均敞開,無板壁封擋,便于從各個位置觀賞架上放置的器物.某博古架的部分示意圖如圖7中實線所示,網格中每個小正方形的邊長為1,則下列結論正確的是( _).



圖6

圖7
以A為坐標原點,AD,AJ所在直線分別為x軸、y軸,建立如圖8 所示的平面直角坐標系.


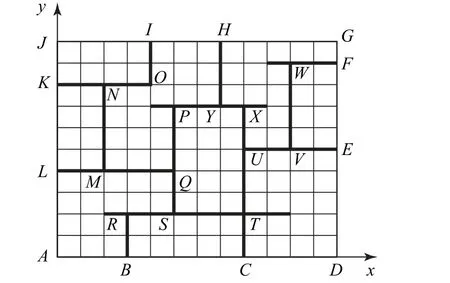
圖8
綜上,選AD.

情境題的背景是多樣的,但來源于現實生活的少之又少,本題就是一道經典題.取現實生活為素材,進行試題命制,體現了命題者的智慧,給學生留下了寶貴的資源,讓學生在理解熟悉情境的基礎上,進一步提升解題能力.
學生能靈活應用數學知識解決各類問題的能力,是為將來在社會生活中用數學解決問題積累經驗,對學生具有一定的挑戰,也考查了學生的數學核心素養,所以好的題目來源于生活.
(完)

