關(guān)注動(dòng)態(tài)立體幾何問題

安 霞

(貴州省都勻第一中學(xué))

1 正方體中的動(dòng)態(tài)問題

例1 如圖1 所示,已知正方體ABCDA1B1C1D1的外接球的表面積為12π,點(diǎn)P在該正方體的對(duì)角面BDD1B1內(nèi)(包括邊界),則下列說(shuō)法錯(cuò)誤的是( ).

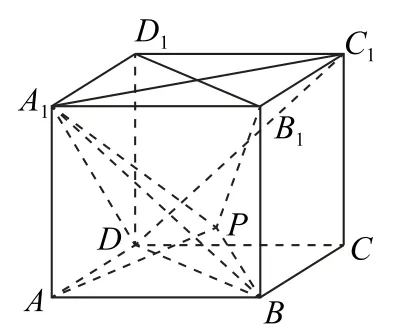
圖1

A.若B1P//平面A1C1D,則點(diǎn)P的軌跡長(zhǎng)度為6

B.若BP⊥平面A1C1D,則點(diǎn)P的軌跡長(zhǎng)度為2 3

C.若點(diǎn)P到平面A1B1C1D1的距離與到點(diǎn)B的距離相等,則點(diǎn)P的軌跡是橢圓的一部分

D.PA＋PA1的最小值為2 3

設(shè)正方體的外接球的半徑為R,則根據(jù)題意知4πR2＝12π,解得R＝3.設(shè)正方體的棱長(zhǎng)為a,則有,即,解得a＝2.

對(duì)于選項(xiàng)A,設(shè)AC∩BD＝O,連接B1O,則易知平面B1AC//平面A1C1D,所以B1O//平面A1C1D.又注意到點(diǎn)P在該正方體的對(duì)角面BDD1B1內(nèi)(包括邊界),若B1P//平面A1C1D,則點(diǎn)P的軌跡為線段B1O(除去端點(diǎn)B1).又△BB1O是直角三角形,所以,則點(diǎn)P的軌跡長(zhǎng)度為6,故選項(xiàng)A 正確.

對(duì)于選項(xiàng)B,連接BD1,易知BD1⊥平面A1C1D,又點(diǎn)P在該正方體的對(duì)角面BDD1B1內(nèi)(包括邊界),所以點(diǎn)P的軌跡為線段BD1(除去端點(diǎn)B).又△BDD1是直角三角形,則,則點(diǎn)P的軌跡長(zhǎng)度為2 3,故選項(xiàng)B正確.

建立全校的安全管理體系。明確網(wǎng)絡(luò)安全責(zé)任制，由校領(lǐng)導(dǎo)牽頭做到分級(jí)管理、自主保護(hù)、責(zé)任明確。各學(xué)院建立網(wǎng)絡(luò)安全員機(jī)制，做到出現(xiàn)問題與信息中心及時(shí)溝通，提高工作效率。信息中心形成網(wǎng)絡(luò)通報(bào)制度，定期對(duì)學(xué)校各系統(tǒng)安全掃描，對(duì)有安全的高危漏洞進(jìn)行通報(bào)，并提出整改方案。對(duì)事發(fā)的安全事故要及時(shí)做出通報(bào)，并協(xié)助處理安全問題。落實(shí)網(wǎng)絡(luò)安全考核制度，對(duì)各部門的網(wǎng)絡(luò)管理員建立評(píng)分與問責(zé)制度，明確各部門的網(wǎng)絡(luò)安全的負(fù)責(zé)人，將責(zé)任落實(shí)到人。

對(duì)于選項(xiàng)C,作PQ⊥B1D1,垂足為Q,則PQ⊥平面A1B1C1D1,所以點(diǎn)P到平面A1B1C1D1的距離就是線段PQ的長(zhǎng)度,也就是點(diǎn)P到直線B1D1的距離.根據(jù)點(diǎn)P到平面A1B1C1D1的距離與到點(diǎn)B的距離相等,可知點(diǎn)P到直線B1D1的距離等于到點(diǎn)B的距離.根據(jù)拋物線的定義,可知點(diǎn)P的軌跡是拋物線的一部分,故選項(xiàng)C錯(cuò)誤.

對(duì)于選項(xiàng)D,設(shè)A1C1∩B1D1＝O1,連接PO1,則A1C1⊥平面BDD1B1,且PO1?平面BDD1B1,所以A1C1⊥PO1.又點(diǎn)O1為線段A1C1的中點(diǎn),所以PA1＝PC1,則PA＋PA1＝PA＋PC1≥AC1＝2 3,所以PA＋PA1的最小值為2 3,故選項(xiàng)D正確.

綜上,選C.

本題以熟悉的正方體為載體,靈活設(shè)計(jì)動(dòng)點(diǎn),對(duì)解題能力要求較高.其中選項(xiàng)A 和B均考查了動(dòng)點(diǎn)的軌跡長(zhǎng)度,需要先明確動(dòng)點(diǎn)的軌跡,再求解其長(zhǎng)度;選項(xiàng)C的求解充分體現(xiàn)了轉(zhuǎn)化思想與拋物線定義的綜合運(yùn)用;求解選項(xiàng)D 的關(guān)鍵是分析出PA1＝PC1,這樣有利于靈活運(yùn)用三角形三邊關(guān)系探求目標(biāo)最小值.

2 圓錐中的動(dòng)態(tài)問題

例2 (多選題)如圖2所示,已知圓錐PO中,PO為高,AB為底面圓的直徑,圓錐的軸截面是面積為2的等腰直角三角形,C為母線PA的中點(diǎn).點(diǎn)M為底面上的動(dòng)點(diǎn),且OM⊥AM,點(diǎn)O在直線PM上的射影為H.當(dāng)點(diǎn)M運(yùn)動(dòng)時(shí),下列說(shuō)法正確的是( ).

圖2

A.三棱錐M-ABC體積的最大值為

B.直線CH與PA不可能垂直

C.點(diǎn)H的軌跡長(zhǎng)度為π

D.AH＋HO的值小于2

對(duì)于選項(xiàng)B,由PO為圓錐的高可知PO⊥AM,又OM⊥AM,PO∩OM＝O,所以AM⊥平面POM,故AM⊥OH.由點(diǎn)O在直線PM上的射影為H,可知OH⊥PM,又AM∩PM＝M,所 以O(shè)H⊥平 面PAM,所以O(shè)H⊥PA.因?yàn)辄c(diǎn)C是Rt△PAO斜邊的中點(diǎn),所以PA⊥CO.又OH∩CO＝O,所以PA⊥平面COH,則PA⊥CH,故選項(xiàng)B錯(cuò)誤.

對(duì)于選項(xiàng)C,因?yàn)镻A⊥平面COH,且經(jīng)過(guò)點(diǎn)C與PA垂直的平面僅有一個(gè),所以點(diǎn)H的軌跡一定在平面內(nèi).由OH⊥平面PAM,可知OH⊥CH,所以點(diǎn)H的軌跡是以CO為直徑的圓(除去C,O兩點(diǎn)),又,所以點(diǎn)H的軌跡長(zhǎng)度為π×CO＝π,故選項(xiàng)C正確.

綜上,選ACD.

本題以圓錐為背景,靈活設(shè)計(jì)動(dòng)點(diǎn)問題,側(cè)重考查空間想象能力、推理論證能力以及運(yùn)算求解能力.在選項(xiàng)A 中,關(guān)鍵是求解點(diǎn)M到平面ABC的距離的最大值;選項(xiàng)B 側(cè)重考查了線面垂直的判定和性質(zhì)在解題中的靈活運(yùn)用;判斷選項(xiàng)C 的關(guān)鍵是準(zhǔn)確分析點(diǎn)H的軌跡是什么圖形;選項(xiàng)D 綜合考查了立體幾何與柯西不等式的綜合運(yùn)用,對(duì)能力的要求較高.

3 翻折過(guò)程中的動(dòng)態(tài)問題

例3 如圖3所示,在矩形ABCD中,AB＝3,AD＝3,現(xiàn)將△ACD沿直線AC向上翻折(如圖4).在翻折過(guò)程中,當(dāng)點(diǎn)D到點(diǎn)B的距離在內(nèi)變化時(shí),點(diǎn)D的運(yùn)動(dòng)軌跡形狀為_________.

圖3

圖4

如圖5所示,過(guò)點(diǎn)D作DF⊥AC,垂足為F,設(shè)DF的延長(zhǎng)線與AB交于點(diǎn)G,過(guò)點(diǎn)B作AC的平行線與DG的延長(zhǎng)線交于點(diǎn)E.將△ACD沿直線AC向上翻折,結(jié)合圖6可知始終有AC⊥DF,AC⊥FE,又DF∩FE＝F,所以AC⊥平面DFE.又過(guò)點(diǎn)F與直線AC垂直的平面唯一存在,所以點(diǎn)D的軌跡必在平面內(nèi).注意到線段DF的長(zhǎng)度保持不變,從而可知點(diǎn)D的軌跡是以F為圓心,且以為半徑的一段圓弧.

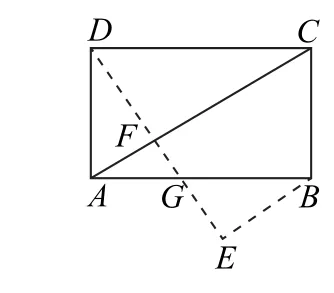
圖5

圖6

解題的關(guān)鍵是通過(guò)巧作輔助線,充分利用翻折過(guò)程中的“不變性”,準(zhǔn)確判斷點(diǎn)D的運(yùn)動(dòng)軌跡.

關(guān)注動(dòng)態(tài)立體幾何問題可幫助我們熟悉此類問題的常見考查方式,明確常用解題方法,有利于進(jìn)一步強(qiáng)化空間想象能力、邏輯推理能力、運(yùn)算求解能力以及立體幾何與其他知識(shí)的綜合運(yùn)用能力.

(完)