基于DDPG算法的電動拖拉機雙電機耦合傳動參數優化*
張勇剛,劉孟楠,胥文翔,徐立友
(1.河南科技大學車輛與交通工程學院,河南洛陽,471003; 2.洛陽拖拉機研究所有限公司,河南洛陽,471039)
0 引言
中國正處于綠色農業的轉型時期,在碳達峰、碳中和的環境政策下,農業機械對排放與效率的要求變得更加嚴格[1]。農業生產中對農作物產量和品質的要求越來越高,在農業機械領域對拖拉機的精準控制與自動化作業提出了更高的要求,而電動拖拉機在精準控制和綠色農業中發揮著重要作用,因此提高電動拖拉機的傳動系統性能已經成為重要的研究方向[2-3]。
國內外學者已經在電動拖拉機做了大量的工作,Chen等[4]提出了一種基于雙電機耦合驅動模式的電動拖拉機動力傳動系統參數匹配與優化設計方法;李書苑等[5]對多種雙電機耦合方案進行參數化建模,有限元分析,并結合動力學評估最終選出一種最優傳動方案;Li等[6]建立了雙電機電動拖拉機傳動系統的數學模型,采用對偶的協調控制策略對電機驅動系統進行設計,得到了雙電機的功率分配規律;徐立友等[7]采用基于模塊的設計方法,搭建了可滿足90 km以下的電動拖拉機綜合測試平臺,為電動拖拉機測試提供了設備支撐;盛繼新等[8]采用雙擋機械自動變速器(AMT)的傳動方案,建立了多目標遺傳算法的參數匹配模型,為優化雙速比自動變速器提供了參考。
綜上所述,雙電機耦合傳動系統經過不斷的論證和發展逐漸成為電動拖拉機一種主流的傳動方案,但是傳動系統耦合速比的優化研究較少;本文以東方紅1804拖拉機為研究對象,通過靜態計算在滿足拖拉機各項性能的前提下求出傳動系列最小傳動比;然后利用Simscape搭建雙電機耦合傳動模型,并且在Simulink中搭建電動拖拉機仿真環境;在靜態優化的基礎上,采用DDPG算法在運輸模式與旋耕模式對雙電機耦合傳動比進行動態優化,得到傳動比的最優值。
1 雙電機耦合傳動結構方案
電動拖拉機雙電機耦合傳動系統結構三維模型如圖1所示。驅動電機和PTO電機連接在變速器的前部;主輸入軸和副輸入軸一端連接在變速器殼體上,另一端分別連接在行星架太陽輪上;行星架作為動力輸出元件,分別輸出給主減速器和PTO軸。

圖1 電動拖拉機動力耦合三維結構
雙電機耦合傳動原理如圖2所示,當PTO軸負載較大時,主電機動力將通過中間軸傳遞給PTO軸;當驅動軸負荷較大時,PTO電機將動力通過中間軸傳遞給驅動軸;最終驅動力通過主減速器傳遞到后橋;在運輸模式和旋耕模式下,兩個同步器和兩個制動器能夠組合出四種動力傳遞路線。
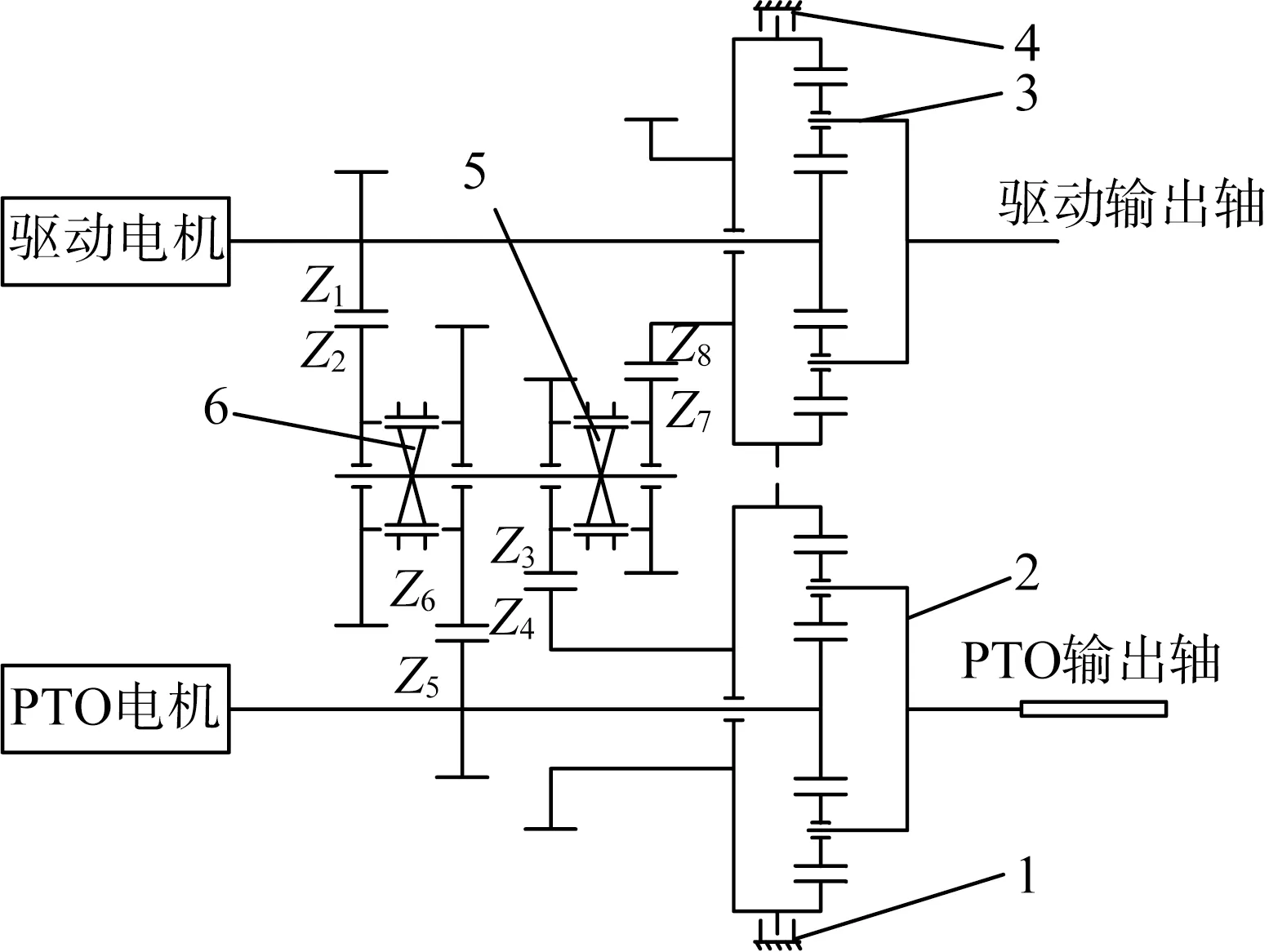
圖2 雙電機驅動系統原理圖
2 傳動系統驅動模式與參數計算
2.1 驅動模式
拖拉機有三種典型工作模式即運輸模式、耕犁模式、旋耕模式,其中運輸模式和耕犁模式都屬于大負荷拖拽作業,并且動力都是通過驅動輪輸出,因此在優化計算中只計算一種模式[9]。
在運輸模式下,PTO軸無動力輸出;當拖拉機需求的動力較小時,動力由驅動電機單獨提供;此時為驅動電機單獨驅動;動力由主電機傳遞到驅動軸,齒圈鎖死,通過主減速器傳遞到車輪;利用杠桿法[10]與圖論法[11]得出轉速與轉矩,計算如式(1)所示。
(1)
式中:nq——驅動電機輸出轉速,r/min;
nb——輸出到半軸的轉速,r/min;
Tq——驅動電機輸出轉矩,N·m;
Tb——輸出到半軸的轉矩,N·m;
k——行星輪系特性參數;
ia——主減速器傳動比。
當拖拉機需求的動力超過驅動電機的高效區間時,PTO電機參與驅動,轉矩、轉速計算如式(2)所示。
(2)
式中:np——PTO電機輸出轉速,r/min;
i56——PTO電機輸入軸到中間軸傳動比,r/min;
i78——中間軸到驅動軸齒圈傳動比,r/min;
Tp——PTO電機輸出轉矩,N·m。
在旋耕模式下,拖拉機驅動輪既要輸出驅動力,PTO軸又要輸出旋轉動力;要同時考慮兩種動力輸出;但是考慮到旋耕模式下,拖拉機前進阻力較小,動力主要從PTO輸出,因此主要討論PTO的動力輸出。
當PTO功率需求較小時由PTO電機單獨提供動力,PTO轉速、轉矩計算如式(3)所示。
(3)
當PTO軸負荷超過PTO電機的高效區間時,驅動電機將一部分動力傳遞到PTO軸,PTO軸轉矩、轉速計算如式(4)所示。
(4)
根據拖拉機的典型工作模式,切換相應的控制器,改變動力耦合方式,對于運輸模式和旋耕模式,驅動系統元件動作順序如表1所示。

表1 不同作業工況電動拖拉機控制元件動作表
2.2 傳動系統參數選取
為同時滿足彎曲疲勞強度和接觸疲勞強度,齒輪模數按齒根彎曲疲勞強度設計;分度圓直徑按齒面接觸疲勞強度設計。
(5)
式中:d1t——試算分度圓直徑;
KHt——試選載荷系數;
φd——齒寬系數;
T1——主動齒輪傳遞轉矩;
u——傳動比;
ZH——區域系數;
ZE——彈性影響系數;
Zε——重合度系數;
Zβ——螺旋角系數;
σH——接觸疲勞許用應力。
利用以上計算方法,參考東方紅1804拖拉機性能參數,根據拖拉機作業功率需求和變速器結構原理圖通過靜力學計算得出齒輪參數配置表,如表2所示。
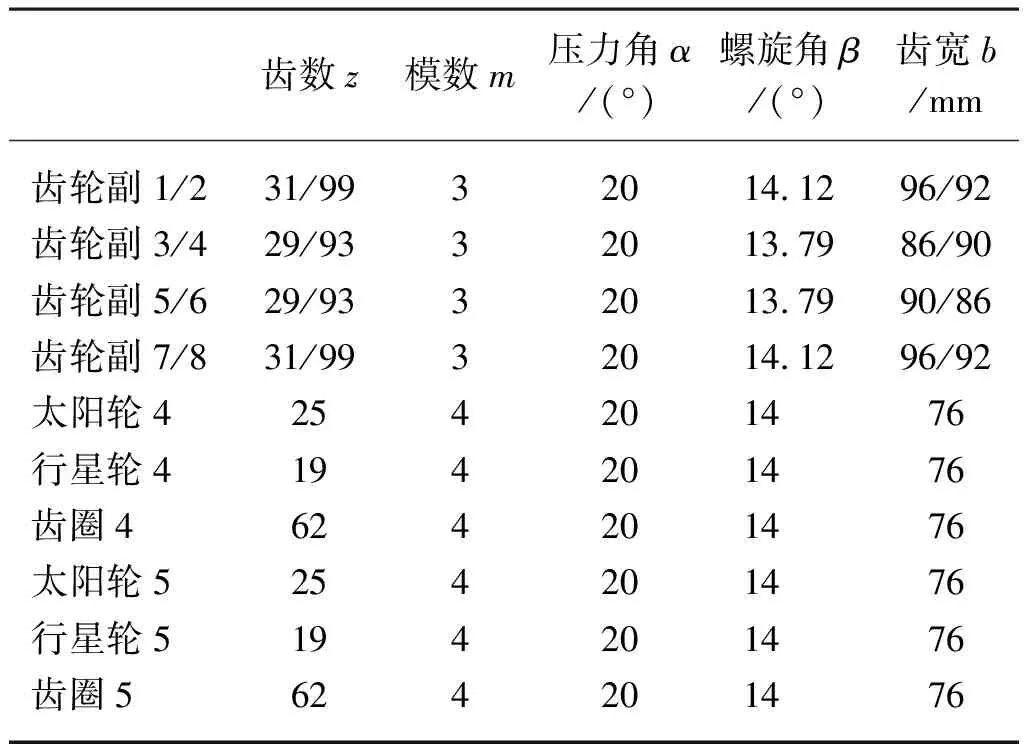
表2 動力耦合裝置主要參數
3 仿真模型搭建
3.1 電機效率模型
動力系統采用了兩臺永磁同步電機,選擇合適的型號,避免功率過剩造成浪費[12];本文根據東方紅1804拖拉機的功率需求,通過動力匹配得到驅動電機和PTO電機主要參數,如表3所示。

表3 雙電機耦合傳動系統主要參數
為了獲得電機效率模型,搭建了測試平臺,通過臺架試驗測出轉速、轉矩和母線電壓、電流,電機效率計算式如式(6)所示。
(6)
式中:Pout——電機機械輸出效率;
Pin——電機輸出功率;
U——母線電壓;
I——母線電流;
Tm——電機轉矩;
nm——電機轉速。
通過試驗測出電機在對應轉速和轉矩下效率的數據,驅動電機,PTO電機效率如圖3所示。根據電機效率模型得出驅動電機高效工作區間集中在800~2 500 r/min,PTO電機高效工作區間集中在2 000~4 500 r/min;符合拖拉機工作需求。
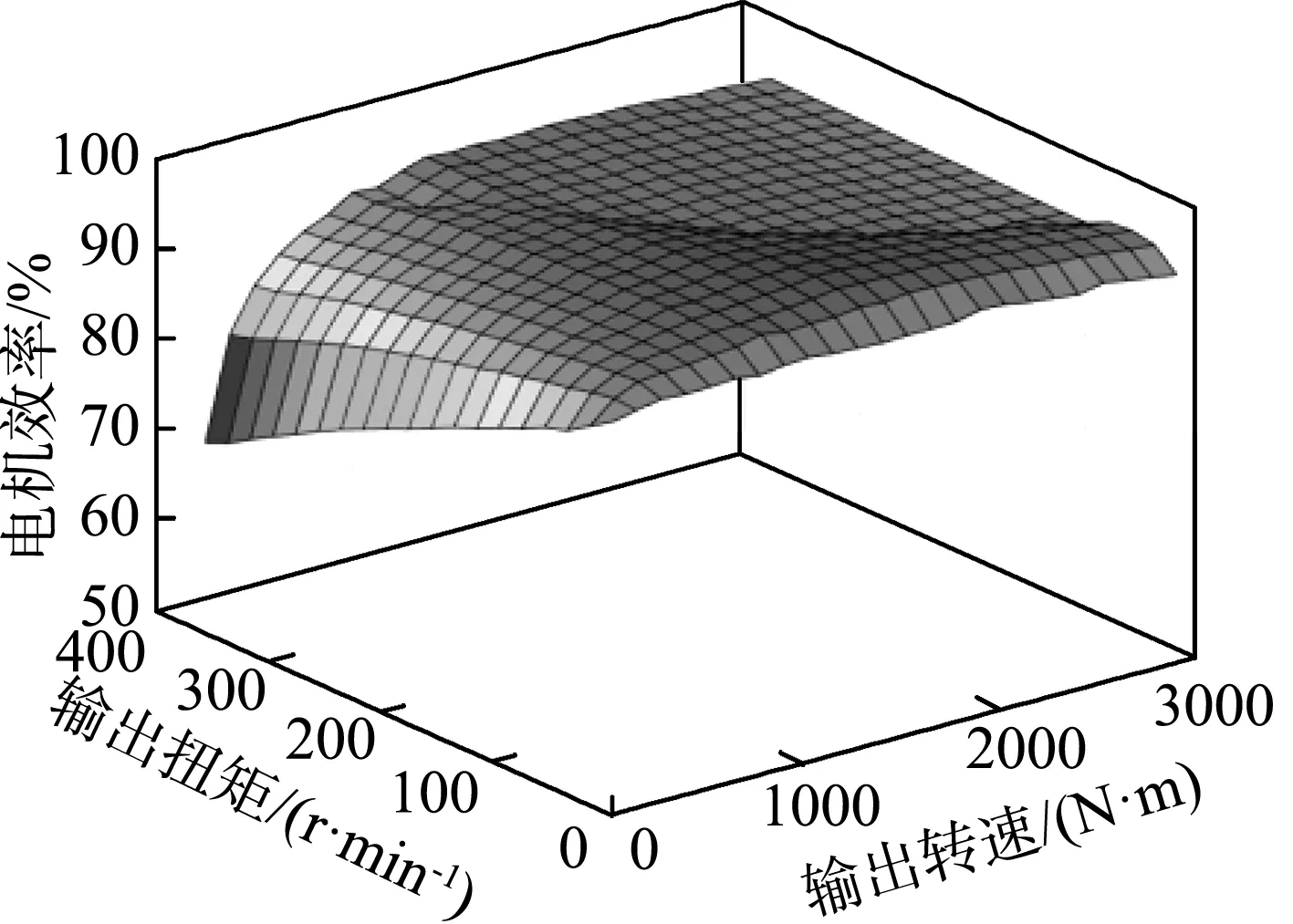
(a) 驅動電機
3.2 搭建DDPG算法模型
深度確定性策略梯度網絡(Deep Deterministic Polity Gradient,DDPG)算法是一種無模型、非策略的強化學習方法;能夠利用模型的輸入和輸出數據在自我學習的基礎上建立被控對象的數學模型,通過系統反饋給被控對象并實現最優控制。DDPG算法是DQN和策略梯度的結合算法,不僅可以實現DQN單步更新,而且保持了確定性政策梯度數據的高利用率和優勢的趨同;觀測空間支持連續與非連續兩種狀態,動作空間支持連續狀態;非常適合電動拖拉機耦合傳動的狀態仿真;DDPG算法流程與模型配置如圖4所示。
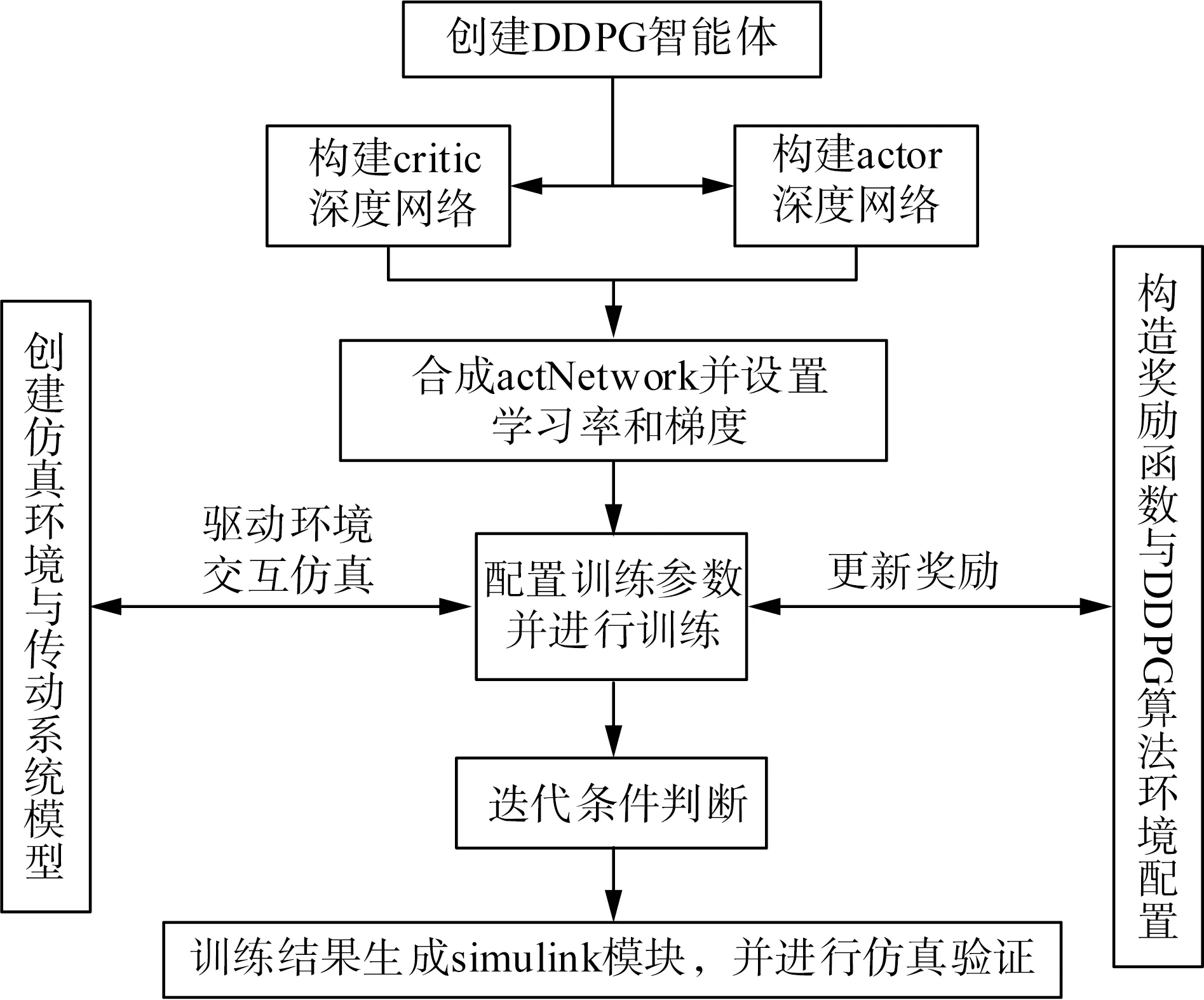
圖4 模型與優化算法工作流程
函數的目標值為執行獎勵值與未來折扣到當前獎勵的和;為了計算累積獎勵,智能體將下一個觀測從抽樣經驗傳遞給目標動作來計算下一個動作,在通過將下一個動作傳遞到critic來獲得累積獎勵。通過最小化所有采集應驗的損失來更新critic參數。使用下面的采樣策略梯度更新執行參數,以最大化預期折扣回報。
(7)
式中:Gai——critic輸出相對于actor網絡計算的動作的梯度;
Gπi——actor輸出相對于actor參數的梯度;
?θ——每個批次計算的獎勵值;
M——每個批次計算個數;
Si——觀測值;
θ——隨機參數值。
在獎勵函數的設計中考慮了4個參數,分別是驅動電機的效率、PTO電機效率、目標車速跟隨誤差和總傳動比,并由4個參數構建獎勵函數,如式(8)所示。
r=-(0.1Ed+0.1Ep+0.3Es+0.05R2)+100B
(8)
式中:r——單次循環獎勵值;
Ed——驅動電機效率;
Ep——PTO電機效率;
Es——實際車速與目標車速的差值;
R——耦合傳動比;
B——動作空間邊界值。
在m腳本中配置算法環境、仿真時間和步長;構建critic和actor深度網絡框架,使用rlDDPGAgent函數生成智能體,配置智能體訓練參數;在simulink中搭建算法模型,為算法訓練創建環境接口;設置觀測器模塊,評價器模塊和動作模塊。
3.3 雙電機耦合驅動系統模型
耦合傳動模塊如圖5所示。
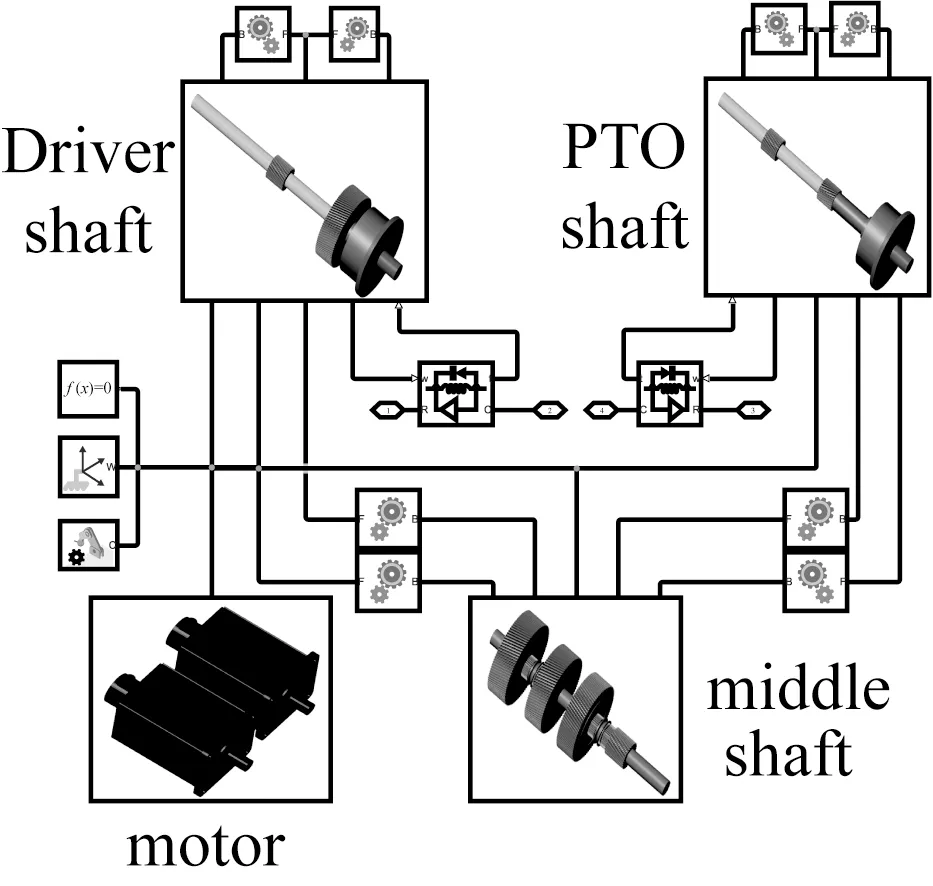
(a) Simscape物理模型
在SOLIDWORKS中構建動力耦合機構參數化模型;將模型文件導入Simscape中;調整模塊位置關系,添加轉動約束與齒輪約束,添加物理驅動信號,驗證傳動系統符合設計要求。添加驅動力后運行物理模型,輸入軸將在驅動電機扭矩的作用下進行轉動,經過齒輪傳動將動力從行星架輸出,通過測量輸出驗證模型。
3.4 搭建電動拖拉機仿真環境
設置電動拖拉機為后輪驅動,添加魔術公式輪胎,路面傾斜角度為,忽略空氣阻力;建模中僅考慮拖拉機縱向力構建拖拉機參數化模型[13-14]。通過采集駕駛員加速踏板、制動踏板和PTO操縱開關的信號,在Stateflow實現工作模式切換,仿真環境模型如圖6所示。
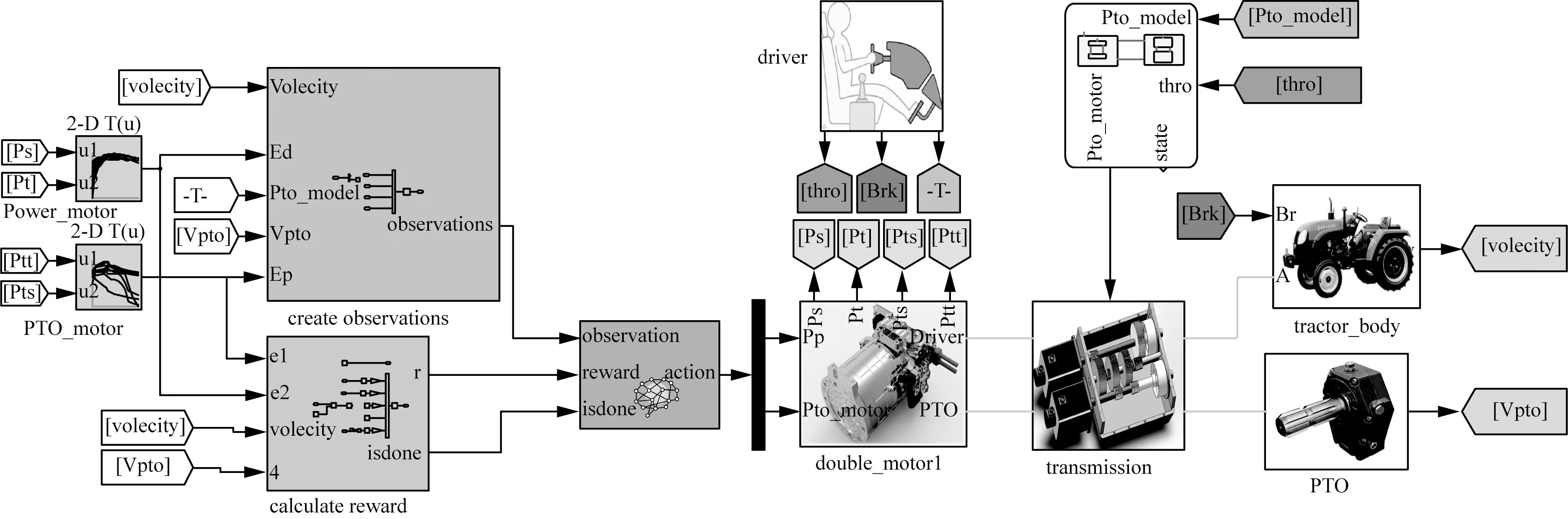
圖6 電動拖拉機仿真環境模型
仿真環境中分別建立了駕駛員模型,雙電機模型,傳動系統模型,拖拉機運動模型以及模式切換模型。
4 齒輪速比仿真分析
在傳動系統結構和動力選型參數確定以后,齒輪速比的選擇是影響拖拉機性能的重要因素,齒輪速比的優化是一個多目標多變量優化問題[15-18];在靜態優化的基礎上借助拖拉機動態工況能夠調節齒輪速比在可行域的偏移,求出在動態優化約束條件下的最優值。
4.1 運輸模式
訓練采用兩種代表工況,在運輸模式下,拖拉機被施加恒定載荷,車速從0加速到20 km/h過程中,PTO電機動力經過Z5/Z6,Z7/Z8與驅動電機動力耦合傳遞到驅動軸。在訓練過程中兩個電機的功率耦合關系由DDPG算法訓練生成,保證每對傳動比都匹配適合的功率耦合關系,排除固定的功率耦合關系對不同傳動比的影響,提高最優傳動比的可靠性。訓練結果如圖7所示。
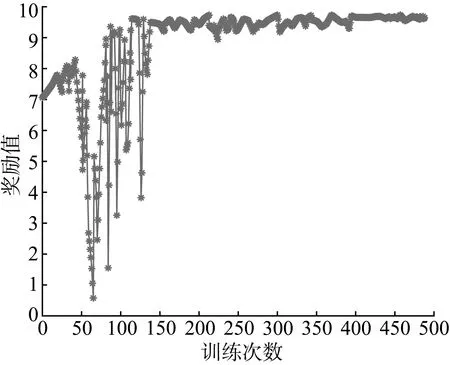
(a) 評價值與訓練周期關系
在訓練次數接近500次時評價值逐漸趨于穩定,此時獎勵最大,兩對齒輪傳動比如圖7(b)所示;可以看出此時Z5/Z6速比逐漸穩定在3.2,Z7/Z8速比逐漸穩定在2.5;根據仿真結果得出運輸模式下優化后的傳動比相比優化前降低了0.7;通過傳動系統參數匹配,確定Z5/Z6的齒數比為30/96,Z7/Z8的齒數比為34/80。通過優化前后仿真對比得到驅動電機和PTO電機控制關系與效率,如圖8所示。

(a) 靜態優化Z5/Z6=26/93,Z7/Z8=31/99
動態優化下拖拉機最先加速到20 km,比靜態優化下提前0.3 s;加速過程與勻速行駛過程中靜態優化下電機平均效率為82%,動態優化下電機平均效率為92%,電機效率提升了10%。
4.2 旋耕模式
在旋耕模式下,對PTO軸施加固定載荷,拖拉機加速到15 km/h后勻速前進,此時拖拉機工作模式由1迅速切換為2,驅動電機部分動力經過Z1/Z2和Z3/Z4傳遞到PTO軸;拖拉機加速到15 km/h后并保持勻速行駛。經過訓練得到最佳傳動比關系如圖9所示,經過500次仿真,Z1/Z2的速比穩定在2.6,Z3/Z4穩定在2.2,由傳動系統參數匹配確定Z1/Z2的齒數比為34/88,Z3/Z4的齒數比為36/79。旋耕模式下優化后的傳動比降低了1.6。

(a) 旋耕模式訓練次數
分別在兩種不同的傳動比下,仿真得出對應的驅動電機和PTO電機的控制規律與效率,如圖10所示。PTO軸采用定轉速輸出模式,從仿真結果得出,在動態優化和靜態優化下PTO軸都能很快地達到350 r/min,并且能夠保持穩定輸出;動態計算下拖拉機2.5 s時達到目標車速15 km/h,靜態優化下3.5 s時達到目標車速,加速時間提前了1 s;動態計算下驅動電機,PTO電機工作的平均效率為95%,比靜態優化下提高了5%。
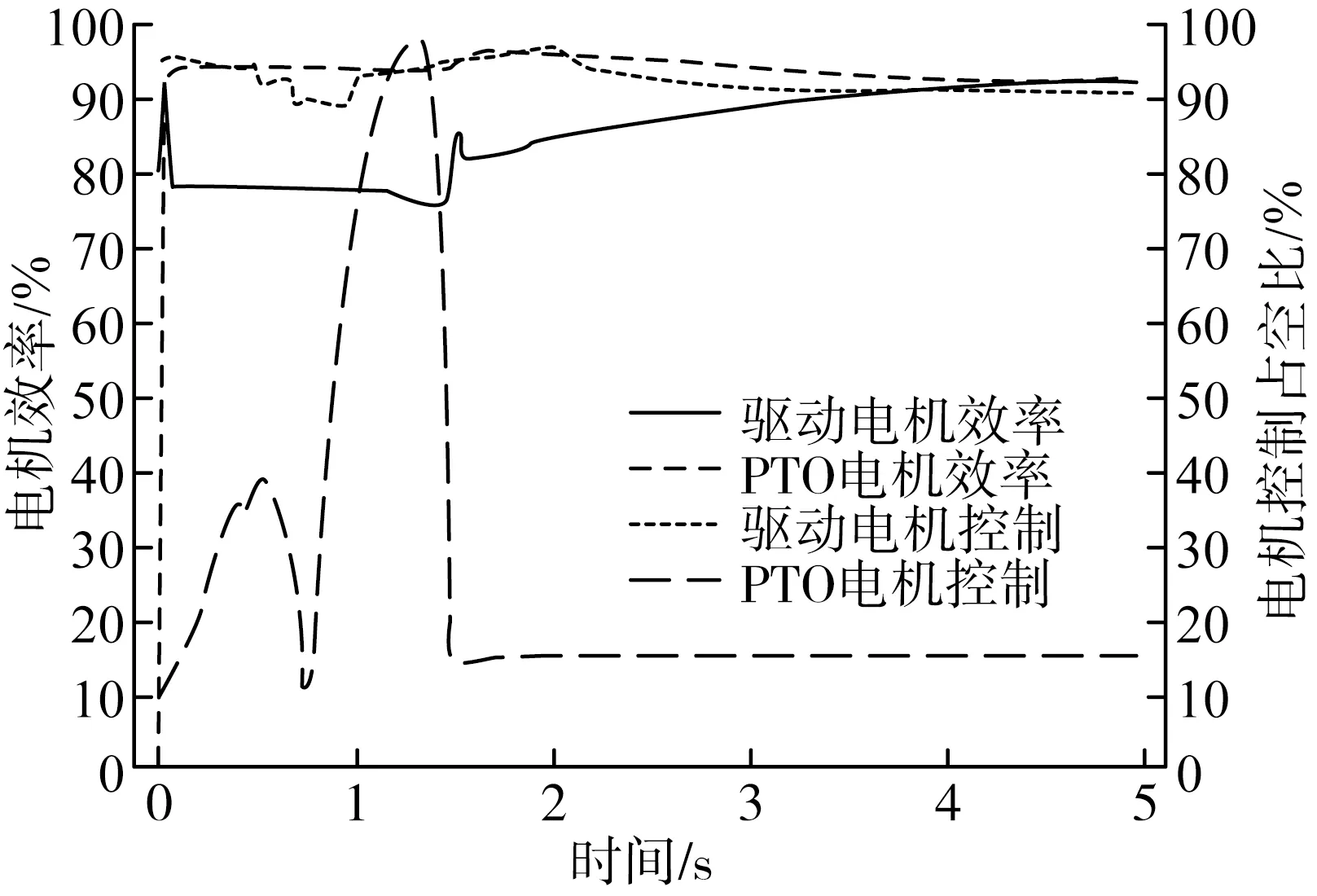
(a) 靜態Z1/Z2=31/99,Z3/Z4=29/93
5 結論
1) 依據東方紅1804拖拉機參數,通過靜態計算確定電機選型與雙電機耦合傳動系統速比;然后對雙電機耦合傳動系統建模,采用DDPG算法,以耦合傳動比最小,加速時間最短,電機效率最高構建目標函數;通過Simscape搭建拖拉機傳動系統模型關聯到Simulink中創建的拖拉機仿真環境;迭代過程中自動匹配電機耦合規律,排除因固定耦合規律對不同傳動比的影響。
2) 選擇在較大負荷下的運輸模式和旋耕模式進行優化,動態優化結果顯示:在運輸模式下,傳動比下降了10.9%,拖拉機從0~20 km/h時間提前了13.6%,電機綜合效率提升10%。在旋耕模式下,傳動比下降了25%,拖拉機從0~15 km/h時間提前了28.5%,電機綜合效率提升5%,PTO跟隨性能優化前后基本保持一致。

