從自動計算的可行性看數據與表征

陳凱 上海市位育中學

0這個數字可能有很多含義，有時候用來代表沒有，有時候用來代表正數和負數交界的那個特殊的數字，在很多程序語言中，0這個數字代表布爾值的“假”，但有時候也用來代表函數運行成功。人們可以在頭腦中輕松地進行0*x這樣的數學運算，或者0andx這樣的邏輯運算，當然，用計算機也可以輕松地做到這些，但這種輕松掩蓋了事情背后的實際情況。若將當前的計算機拆解至晶體管那樣細小的程度，盡管復雜，還是能夠觀察到機器是如何將某種低電壓作為0、高電壓作為1（或者其他對應方式）從而控制開關電路實現信號的傳遞和計算的——相對而言，倒是人頭腦內部的工作情況更難以直觀地顯現出來。周以真說，“計算思維是人的思維方式而不是計算機的思維方式”，“計算思維是思想，不是人造物。不只是我們生產的軟件硬件等人造物將以物理形式到處呈現并時時刻刻觸及我們的生活，更重要的是還將有我們用以接近和求解問題、管理日常生活、與他人交流和互動的計算概念”[1]，對這些話的理解也許會產生分歧，但筆者從中得到一個重要的啟發，就是在求解問題的過程中，可以先將以物理形式的時時刻刻觸及我們的軟硬件人造物——這個人造物基本上就是人們日常使用的計算機——先行排除出去，而將目光放置在計算得以實現的概念上。在周以真的原文中，“計算概念”一詞是“computational concepts”，指的是與計算機有關的諸多概念，這提示了求解問題過程中概念先行的重要性。本文圍繞二進制編碼的數據與數據的表征方式，從概念出發對求解問題的計算裝置進行設計和創造，討論將這樣的過程用于信息技術教學的可能性。

●交替轉向行為與計算

這里給出一個稍微有點奇怪的例子，有一種甲殼動物名為鼠婦，除了平時喜歡生活在陰暗潮濕的地方，它還有一種有趣的習性叫做交替轉向行為，如當它行走時遇見障礙，就向右轉彎，又遇到障礙，就向左轉彎，再遇到障礙，就向右轉彎… …如此左右交替。

這種基于條件的行為的變化提示了將其用于計算的可能性，與計算機有關的二進制編碼數據與表征的概念，恰好對應了鼠婦行走過程中要么這樣、要么那樣的二分選擇行為。例如，可以將鼠婦向左轉表示數據0，向右轉表示數據1；或者，將沒有障礙表示數據0，有障礙表示數據1；或者，將鼠婦無法到達目的地作為0，能夠到達目的地作為1。以二進制解碼器為例，假設輸入兩位二進制數，則需要輸出相對應的0、1、2、3這4個十進制數字，在設計裝置之前，就需要思考如何實現對數據的表征。輸入部分相對容易處理，因為數據可以和鼠婦行為的兩種狀態進行直接對應；輸出部分則比較困難，因為需要找到對應兩位二進制數的4個數字的4種狀態。

圖1展示了一種設計方案：用積木擋板建造一個“迷宮”，將鼠婦放置其中，在迷宮中，標為B的擋板表示二進制數的第一位（低位），標為A的擋板表示二進制數的第二位（高位），擋板撤走代表數字0，擋板放下代表數字1，這樣，鼠婦最終行走的方向就可以用來指示兩位二進制數所代表的4個不同的數字。由于鼠婦在不同環境中的行走路徑不同，可以在“迷宮”周圍放置若干個“蘋果”標記，通過觀察鼠婦觸碰到哪個蘋果來獲知計算的結果，如圖2所示。在現實中，生物的這種強迫性的交替轉向行為因各種因素的影響，是存在一定出錯概率的[2]，這里假設鼠婦會以一種理想的狀態嚴格遵守交替轉向的行為規則。為了讓鼠婦的行動更直觀地顯現出來，可以編寫一個簡單的程序來進行模擬。

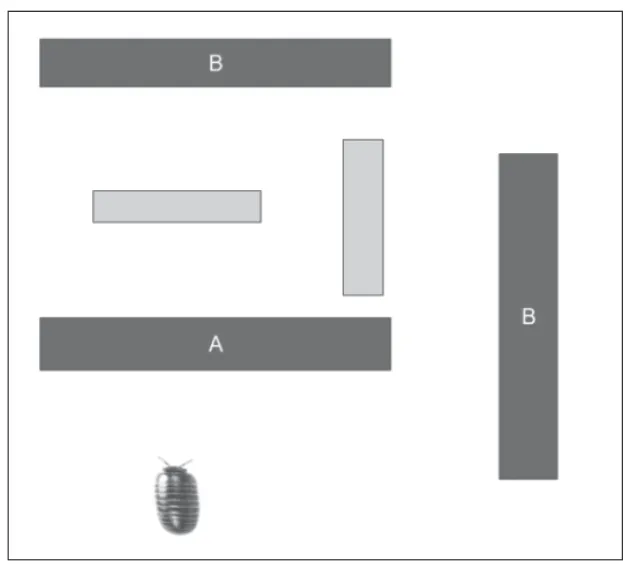
圖1 初始狀態下的擋板和鼠婦

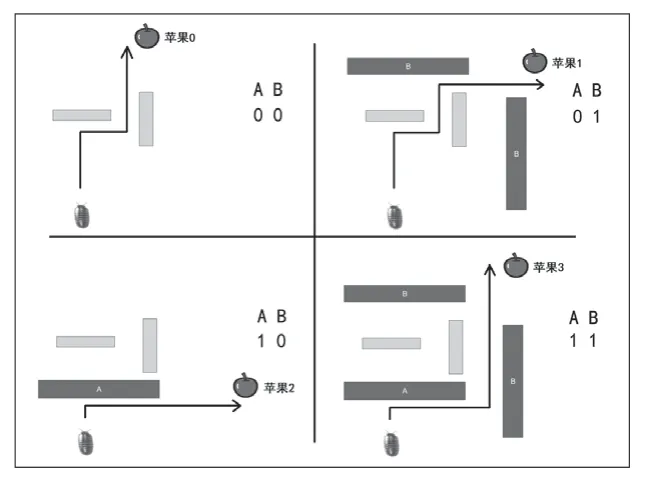
圖2 對應兩位二進制數4種情況的鼠婦行走路徑

上面的例子是用兩塊擋板的有和無代表兩個二進制數1或0，來實現二進制解碼運算。其實，也很容易借助類似的方法來實現邏輯運算。與邏輯運算和或邏輯運算裝置的設計

都非常容易實現，這里就不占用篇幅介紹了。相對難一些的是異或邏輯運算，其裝置構造仿佛一種智力游戲，圖3給出一種可行的設計：當擋板A或擋板B其中之一被撤除后，鼠婦就能走到蘋果的位置，表示結果為1；當兩塊擋板都保留或都被撤除后，鼠婦就無法走到蘋果的位置，表示結果為0，這樣，鼠婦在走迷宮的過程中就實現了異或運算。接下來還可以進一步加以擴展，將異或運算和與運算結合起來，實現一個二進制加法裝置，如圖4所示。

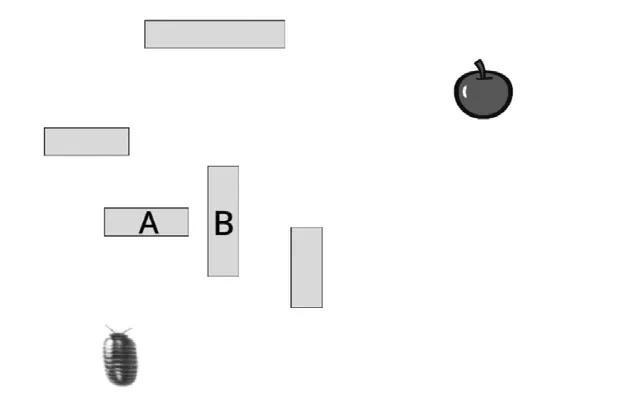
圖3 一種異或邏輯運算的設計

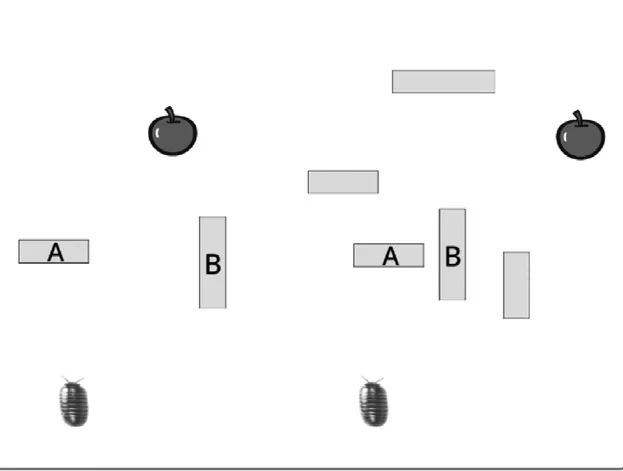
圖4 一種加法運算裝置的設計

●鼠婦計算裝置中的數據和表征

仔細分析二進制編碼數據與表征，就可以發現存在多種不同的情況：可以用二進制數據表征某個十進制的數據，如二進制數101表示存在5塊積木擋板；或者用二進制編碼的數據來表征特定的事物狀態，如某個位置有積木擋板，可以用數字1表示，某個位置沒有積木擋板，可以用數字0表示。本文給出的例子恰恰是反過來的，在計算的輸入過程中，用有積木擋板來代表1，沒有積木擋板來表示0。

可以發現，輸出部分的表征方式更為復雜，首先，以鼠婦遇到蘋果來表示1，沒有遇到表示0，4個蘋果接觸與否分別對應了4個一位的二進制數，在計算結束時，只有某一個特定的蘋果被鼠婦接觸，所以這4個二進制數只可能有一個數是1，從而表示其代表的十進制數是0、1、2、3中的某一個。這就是二進制獨熱碼的一種應用，下頁表中列出了解碼過程中這兩層不同的表征。

?

這個計算裝置的使用者不需要知道鼠婦行走的細節，只要知道輸入部分狀態和輸出部分狀態的含義，就可以利用它進行計算了。對設計者來說，所做的事情不只是提取事物共同屬性的抽象化，還需要為某種抽象過程能夠被自動執行而進行構造。被構造出來的裝置所做的事就是computing，對應“自動計算”，本文提到的“計算”都是指“自動計算”（為避免用詞混淆，筆者認為創造相應的新詞或許是有必要的，如可以將“自動計算”稱為“器算”，或可以借用舊詞“機算”）。

大衛·查默斯（D a v i d Chalmers）指出信息具有物理形式，他詳細說明了結構化信息和符號信息對于二進制編碼的數據表征事實的過程，舉例說，“110111”中存儲器（其物理形式是穿孔卡片上特定位置的孔）的某個特定的部分，才代表某人年齡是55歲。[3]在這里，存儲器中數據的位置是一種結構化信息，闡述哪個位置對應年齡是一種符號信息，然后才能使二進制序列串表征55歲的事實。在本文的例子中，獨熱碼是一種結構化信息，其具體的物理形式是鼠婦是否觸碰蘋果。而對于這種結構的解讀，也就是獨熱碼中1的位置怎樣對應十進制數，則是一種符號信息。為了構造某種自動的計算裝置，設計者需要關注結構化信息的物理形式以及對結構的解讀方式。

到目前為止，這個鼠婦計算裝置是不完備的，因為一個完整的計算實現（computing implementation）需要具備可級聯性、扇出性、布爾完備性這樣幾個特征[4]，這里重點圍繞可級聯性開展討論，如當前的這個裝置在輸出部分，采用鼠婦是否遇到蘋果的方式來表示0，這樣做存在一個缺陷——無法將計算結果為0和計算未完成這兩種情況區分開來，于是就無法正確地將計算結果傳遞給下一個系統。另一個問題是，用以表征輸入數據的事物狀態變化形式（有無擋板）和用以表征輸出數據的事物狀態變化形式（鼠婦有無觸碰蘋果）不一致，這樣就很難將此類計算裝置相互連接起來去構造出一個更復雜的計算裝置。

●改進的鼠婦計算裝置

接下來，針對上面存在的問題，對裝置進行改造。其中一個需要調整的地方，是對用以表征數據的材料也就是結構化信息的物理形式進行改造，使其具有一致的表征數據的狀態變化形式。假設輸入和輸出部分都使用擋板來表示，那么在級聯的過程中，就需要設計用鼠婦推動擋板的裝置，顯然，這很為難鼠婦，雖然說設置一個生物感應裝置并借助機械設備來吊裝積木擋板，也能夠實現目的，但這樣就太復雜了。相對而言，若將輸入和輸出都用鼠婦的行為來表征，則更為可行。例如，在圖5的例子中，在實現與邏輯運算的過程中，無論是輸入數據還是輸出數據，都是由是否存在觸碰蘋果的鼠婦來表示的。

圖5 一種用鼠婦行為表征輸入和輸出數據的與邏輯運算裝置

這個與邏輯運算的具體實現過程還是很容易想象出來的，左下角A和B兩個作為輸入的蘋果處，如果都沒有鼠婦，則右側輸出必然沒有鼠婦觸碰蘋果；如果只有一個鼠婦，則這個鼠婦會被困在墻角陷阱中，如果有兩個輸入，當其中一個鼠婦被困于墻角L形陷阱中后，另一個鼠婦觸碰障礙（畢竟另一個鼠婦也是障礙）拐彎，最終到達作為輸出的蘋果位置。這恰好對應與邏輯運算的規則。當然，只有虛擬的理想狀態下才能達到這樣的效果，現實中的鼠婦在幾次碰壁后是會從陷阱中逃脫的。以下各種方案都基于理想狀態下的鼠婦行為，不再一一說明。

當輸入和輸出的事物狀態變化形態統一后，就很容易采用各種簡單的組件相互連接搭建出復雜的系統，如上頁圖6所示的裝置的功能，是用兩個輸入數據進行與邏輯運算，再和第三個輸入數據進行與邏輯運算。

圖6 級聯的與邏輯運算的設計

要實現或運算，就稍微麻煩一些，需要引入一個叫做減速墊的裝置（如圖7）。當左下角A和B兩個作為輸入的蘋果處都只有一個鼠婦時，當然只會有一個鼠婦到達輸出的蘋果位置；如果有兩個輸入，因為減速墊的作用，B處的鼠婦因觸碰A處的鼠婦拐彎，從而無法到達輸出的蘋果位置，最終只會有一個鼠婦到達作為輸出的蘋果位置。

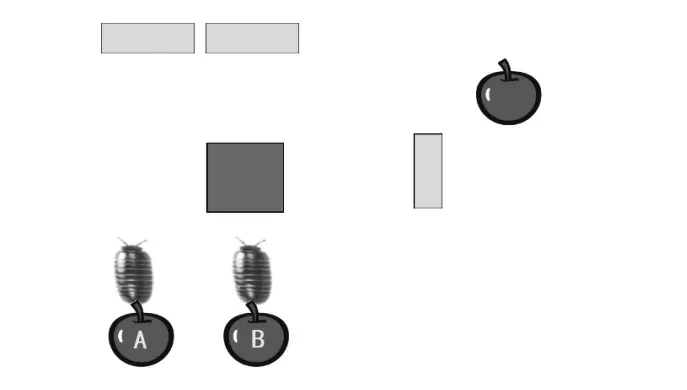
圖7 或邏輯運算的設計

怎樣用鼠婦來實現非邏輯的運算呢？可以引入一個鼠婦作為固定信號，如圖8所示，當輸入信號將這個固定信號攔截掉后，鼠婦就無法到達輸出端，如果沒有輸入信號，這個固定信號就會到達輸出端，于是對應了非邏輯運算。在圖8的例子中，也同時解決了另一個重要的問題，就是要能區分結果為0和尚無結果這兩種情況，解決的方法是再增加一個鼠婦作為計算是否已完成的時間信號，當這個時間信號鼠婦到達用圓圈表示的指定位置時，表示計算結果已經呈現。在這個時間信號的輔助下，可以確保鼠婦未能觸碰蘋果這一狀態，確實表達了計算后0的結果。

圖8 非邏輯運算的設計

借助時間信號和碰撞攔截，不僅可以實現非邏輯的運算，還可以實現其他邏輯運算，如果計算過程中，信號可以復制（假設鼠婦能在某種機構的作用下一分為二），那就能實現所有的邏輯運算功能。在一些生物計算機的設計中，就采用這種碰撞、攔截以及復制信號的方法來實現邏輯運算，限于篇幅這里不展開說明。自然界中許多事物天生具有可計算的特性，復雜的計算過程可以依賴非常簡單的規則和行為構建出來，和本文所列舉的僅存在于紙面上的理想實驗不同，有研究者已用螃蟹群的碰撞來實現了邏輯運算。[5]甚至于不需要生物，依靠無生命的實物如臺球，在理想的無摩擦的狀態下碰撞，也能夠構造出計算裝置。[6]這種現象，被稱為結構化信息的物理基底中立。

本文介紹的計算裝置很容易借助圖形化編程語言來實現，僅用鼠婦、擋板、蘋果、減速墊這些簡單的角色和行為規則，就能模擬出各種功能不同的計算過程，體現出用事物狀態的變化來表征數據的思想方法，希望這種規則簡單、構造和功能多樣的虛擬計算裝置能成為培養和考查計算思維的一種可供選擇的平臺。