分析學情　有序思考　提煉模型　提升素養

程峰　張林

【摘 要】 分析和調查學生在解答一道畫圖題時的困惑和思維盲點，有助于教師深入理解題目，挖掘題目，尋求適合學生解題思路和方法，并提煉出幾何模型，在發展學生思維能力的同時訓練了學生的幾何直觀能力、邏輯推理能力，從而提升學生的數學素養.

【關鍵詞】 思維盲點;幾何模型;問題本質

1 題目呈現

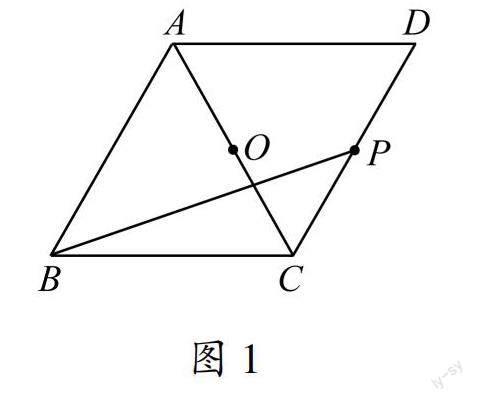
如圖1，在菱形ABCD中，P是CD的中點，O是對角線AC的中點，∠A=120°，連接BP，請僅用無刻度的直尺按要求完成以下畫圖（不寫畫法，保留作圖痕跡）.

（1）在圖1中畫出BC的中點M.

（2）在圖2中畫出線段BP繞點O順時針旋轉60°后的圖形.

本題是筆者所在學校一次模擬考試題.本題以常見的含120°（或60°）角的菱形為背景，圖形簡潔，主要考查旋轉作圖，考查圖形結構的內在邏輯關系，對學生的數學素養要求較高.本題第（2）問得分率很低，不到20％（注：本文主要討論第（2）問，第（1）問略），大部分學生不能確定B點旋轉后的位置.有很多學生憑主觀臆斷，胡亂畫出B點旋轉后的位置，也有很多學生直接畫出旋轉后的線段，沒有畫圖痕跡.

2 學情分析

在教學之前，筆者對學生的錯誤畫法進行了分析，然后隨機抽取不同層次的學生若干名，讓他們談談在考試過程中對于此題遇到的困難或思維盲點.經過交流和分析，筆者發現學生的困惑和思維盲點主要集中在以下三個方面：

（1）無方向：這道題圖形背景簡潔，但簡潔的同時，也給學生增加了難度，很多學生不知道往什么方向思考，毫無頭緒.

（2）無圖形：觀察圖形易知P點繞O點順時針旋轉60°到C點，△POC是等邊三角形，根據旋轉的性質，B點繞O點順時針旋轉后的對應點H，應是以OB為邊的等邊三角形的頂點，也就是畫出另一個等邊三角形，但是很多學生沒想到.

（3）無思路：有學生雖然想到要畫等邊三角形，但是這個等邊三角形如何畫出？B點繞O點順時針旋轉后的位置如何確定？大部分學生找不到畫圖思路.

3 教學實施

3.1 分析圖形特征，初步感知問題

如圖3，為了有效尋找圖形的內在邏輯結構，筆者提出問題：（1）菱形ABCD有什么特殊性質？如果連接OP，能確定△POC的形狀么？（2）你能確定點P繞O點順時針旋轉60°后的位置嗎？（3）你能確定點B繞O點順時針旋轉60°后的大概位置嗎？

教學分析 通過分析圖形特征，在問題串的解決過程中，學生自然發現和構造出符合要求的輔助線，通過思考與嘗試，學生發現∠ACP=60°，且OP=OC，所以首先能確定P點繞O點順時針旋轉60°到C點，△POC是等邊三角形，根據旋轉的性質，B點繞O點順時針旋轉后的對應點H，應是以OB為邊的等邊三角形的頂點.

3.2 轉化問題，尋求突破

問題 OH跟AB存在什么位置關系？

連接OB，由菱形的性質知∠AOB=90°，因此問題轉化為在∠AOB內部畫出以OB為邊，點O為頂點的60°角，即∠BOH=60°，又易知∠ABO=30°，所以∠OGB=90°，也就是OH⊥AB，如圖4，這樣問題又轉化為過點O畫線段OH⊥AB，垂足為點G.

3.3 繼續探究，確定思路

問題：如何確定點G的位置呢？又如何確定點H的位置呢？

要畫出垂線段OH，首先要確定點G的位置，猜想點G會是什么特殊點呢？如圖5，延長PO交AB于點E，則E點是AB的中點，OA=OE，易知∠BOE=∠OBE=30°，所以∠EOG=60°-30°=30°=∠AOG，所以點G是AE的中點（三線合一），這樣就確定了點G的位置.那么點H的位置又如何確定呢？如圖6，延長DA，OG，它們的交點即為點H.連接HE，易證四邊形OEHA，四邊形OEBK都是菱形，且菱形OEHA≌菱形OEBK，OH，OB分別是它們對應的對角線，所以OH=OB，且∠BOH=60°，所以△OBH是等邊三角形，即B點繞O點順時針旋轉60°得到點H.

教學分析 為了讓學生充分理解如何尋找點B旋轉后的位置，筆者將原問題分解成一連串相關問題，使學生從整體上把握問題的本質，獲得解題思路.

3.4 畫法生成，發展思維

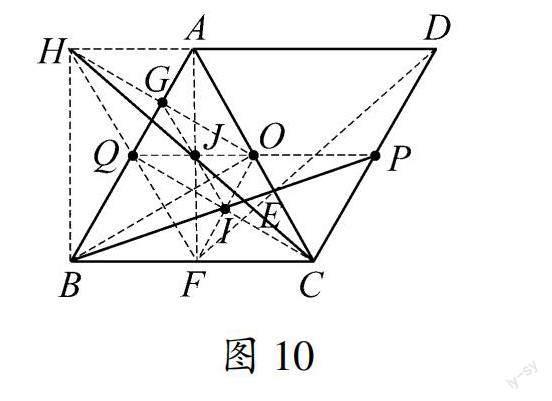
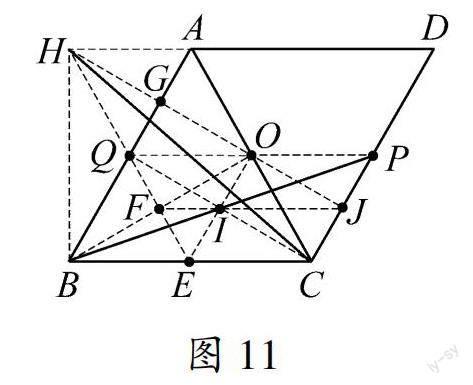
通過前面的思考和探究可知，只要畫出AE的中點，就能畫出B點旋轉后的對應點，那么僅利用無刻度的直尺如何畫出AE的中點呢？筆者放手讓學生合作探究，課堂上得出了以下六種畫法：如圖7—12，各圖中線段HC為線段BP繞O點順時針旋轉60°后的線段.

教學分析 通過循序漸進，抽絲剝繭的分析，最終得出只要畫出AE的中點，就能畫出B點旋轉后的對應點.在整個思考和探究的過程中，使學生知其然，更知其所以然，較好地發散了學生的思維，訓練了學生的幾何直觀能力，邏輯推理能力，從而提升了學生的數學素養.

3.5 提煉模型，理解本質

當旋轉后的線段HC畫出來后，筆者讓學生回顧考試時遇到的困難和思維盲點，哪一步沒想到？為什么沒想到？是知識點遺忘還是方法不當？現在有哪些領悟？你能發現圖7—12中都蘊含的一個模型圖嗎？如果發現了，把它畫出來.當筆者把圖7—12中部分線段隱藏起來，都只留下圖13，學生紛紛感嘆，原來就是特殊的“手拉手”模型圖，原來此題就是把圖13隱藏起來，讓我們畫出來即可.為了讓學生進一步理解圖13，筆者讓學生盡可能的說出圖13的性質：OP=OC，OB=OH，△OPC，△OBH都是等邊三角形，△BOP≌△HOC，BP=HC，BP與HC的夾角是60°，線段HC是由線段BP繞點O順時針旋轉60°得到.筆者把這種畫法形象地稱為“手拉手模型法”，并提醒學生今后在遇到有關線段旋轉的問題，首先可以考慮構造出“手拉手模型圖”.

教學分析 筆者讓學生進行反思，讓學生明白“為什么這樣畫”“怎么想到要這樣畫”等問題，這需要教師引導學生對解題思路的認識不能僅停留在直覺層面，而要上升到理性層面.從畫完后的圖形中提煉出“手拉手”模型，既讓學生發現問題的本質，又是思維上的一次升華.

3.6 運用模型，深化理解

為了進一步使學生理解和運用手拉手模型，筆者趁熱打鐵，提出以下幾道變式問題：

（1）畫出BP繞O點順時針旋轉120°的線段，如圖14所示HK；（筆者提醒學生還是畫等邊三角么？）

（2）畫出BP繞O點逆時針旋轉60°的線段，如圖15所示MH；

（3）畫出BP繞C點順時針旋轉60°的線段，如圖16所示AG；

（4）畫出BP繞A點順時針旋轉60°的線段，如圖17所示HF；

（5）畫出BP繞D點順時針旋轉60°的線段，如圖18所示MG.

教學分析 美國數學教育家G·波利亞曾說“好問題同某種蘑菇相像，它們都成堆地生長，找到一個以后，應當在周圍找一找，很可能附近就有好幾個”.因此，自然想到改變旋轉中心或旋轉角度對原問題進行變式探究，這樣可以達到舉一反三，觸類旁通的效果，讓學生再次感悟“變中有不變”，即問題變了而畫法沒變，仍然是構造“手拉手模型”.學生用已有的方法和經驗解決新問題時，可以進一步感悟畫圖思路，提升解題能力，進一步理解、把握問題本質.

3.7 節外生枝，殊途同歸

正當筆者要結束此題的教學時，一位畫法正確的學生站起來說他的畫法跟筆者講的畫法不同.該生的思路是把BP看作是平行四邊形BCPG的對角線，因此先畫出 圖19BCPG繞點O順時針旋轉60°后的HFCA，連接對角線HC，則HC就是BP繞點O順時針旋轉60°后的線段.如圖19所示.筆者表揚該生能在考試時間緊張的情況下想到旋轉平行四邊形的方法，體現了思維的靈活性、變通性，同時也體現了整體與部分的思想.當然，也可以看作是把△PGB（△PBC）旋轉到△CAH（△CHF）.從最后的畫出的圖形看，本質上還是“手拉手模型法”，用一個成語概括就是“殊途同歸”.

4 教學反思

4.1 分析學情，保障教學有的放失

學生解題時的困惑和思維盲點從某種意義上說也是教學的起點.筆者在教學之前對學生試卷上出現的錯誤予以分析并與若干名不同層次的學生進行交流，通過6個教學環節，層層推進，有序展開，在破除學生心中疑惑的同時成功突破本題的難點，達到了學生知其然更知其所以然的教學效果^[1].由此可見，只有建立在學生學情基礎上的備課，才是有針對性的備課，才是理解學生的備課；只有建立在學生學情上的教學，才能保障教學活動有的放矢.

4.2 有序思考，促進思維能力提升

從本題的各種畫法看，雖然最后畫出的圖形都是常見的手拉手模型，但是從學生的答題情況看，多數學生的思維障礙是難以確定旋轉后的位置，無法與手拉手模型建立聯系，無法將題中的條件進行整合，導致無法畫出旋轉后的圖形.這就需要教師在教學時給予學生充分暴露思維的機會，在思維盲點處加以點撥.教師要引導學生有效審題，有序思考，由“已知”想“可知”，由“未知”想“需知”，找到中間環節，構建思維通道，尋找內在聯系，從而理解問題的本質，最終實現學生思維能力的有效提升^[2].

4.3 提煉模型，揭示問題本質

解題教學要注重對數學模型的提煉.在教學中，充分利用“數學模型”，將學生難以理解的知識進行適當的模型處理，以他們能夠理解和接受的方式呈現出來，與他們的思維水平和已有的知識結構相融，學生就可以實現在最近發展區內對已有的知識的鞏固，同時提煉模型也有利于學生更好地理解問題本質，揭示問題本質.

4.4 變式探究，落實素養提升

變式探究，一方面可以幫助學生鞏固先前的所學知識和方法，另一方面可以拓展學生的視野，使學生更深刻地把握問題結構，理解問題本質.本節課幾個變式問題，既達到了鞏固練習的目的，又拓展了學生的思維；既培養了學生幾何直觀能力、邏輯推理能力，又落實了數學核心素養的提升.

參考文獻

[1]鄭金.貼近學情 提升能力 落實素養[J].中學數學教學參考（中旬）2022（8）；32-34.

[2]徐一鳴.夯基礎 長能力 促思考[J].中學數學教學參考（中旬）2019（4）；45-47.

作者簡介 程峰（1975—），男，中小學高級教師;主要研究初中數學教學.

張林（1985—），女，中小學一級教師;主要研究初中數學教學.