基于三維花卉模型的緯編提花織物設(shè)計(jì)

商林婧, 張愛(ài)軍, 張燕婷

(江南大學(xué) 針織技術(shù)教育部工程研究中心,江蘇 無(wú)錫 214122)

花型意匠圖的繪制是針織服裝設(shè)計(jì)中一個(gè)必不可少的過(guò)程。根據(jù)紋樣結(jié)合織物組織將花型放大并點(diǎn)繪在一定規(guī)格的意匠紙上的圖樣叫作意匠圖。傳統(tǒng)繪制意匠圖的方式都是人工手繪,不僅費(fèi)時(shí)費(fèi)力,而且對(duì)于一些沒(méi)有美術(shù)功底的工作人員來(lái)說(shuō),完成一幅美觀的意匠圖需要花費(fèi)大量的時(shí)間。

在針織意匠圖的設(shè)計(jì)過(guò)程中,花卉作為一種常用的提花圖案,由于其結(jié)構(gòu)復(fù)雜且種類(lèi)繁多,設(shè)計(jì)人員需要耗費(fèi)更長(zhǎng)的時(shí)間來(lái)繪制。因此,針對(duì)現(xiàn)有花卉類(lèi)型的針織意匠圖生成過(guò)程復(fù)雜、耗費(fèi)時(shí)間長(zhǎng)等問(wèn)題,本文提出了一種基于三維數(shù)據(jù)的針織意匠圖生成算法。即將二維的花卉圖片以3D模型的形式呈現(xiàn),再轉(zhuǎn)換為二維圖像自動(dòng)生成意匠圖,無(wú)需手工繪制,在一定程度上可以節(jié)省人力、提高工作效率。近年來(lái),國(guó)內(nèi)外許多學(xué)者針對(duì)基于圖像的花卉建模進(jìn)行了一系列的研究工作,主要是通過(guò)以下方式來(lái)獲取二維圖像缺失的深度信息,如引入幾何投影、用戶(hù)的手繪信息等。Ijiri等[1]將花朵的建模過(guò)程分為幾何編輯與結(jié)構(gòu)編輯兩部分,采用從局部到整體的建模方式組合生成結(jié)構(gòu)復(fù)雜的花朵模型。Xue等[2]采用平面幾何的方法來(lái)擬合物體,并利用物體的對(duì)稱(chēng)性對(duì)生成的點(diǎn)云進(jìn)行優(yōu)化處理。Yan等[3]假定花朵為一個(gè)三維圓錐,通過(guò)該圓錐擬合花朵生成一個(gè)花瓣模板模型,并將模型投影到二維圖像上,對(duì)每個(gè)花瓣進(jìn)行細(xì)節(jié)調(diào)整,重建出十分逼真的花朵模型。繆永偉等[4]通過(guò)交互式建模方法,在圖像上提取花卉的外圍輪廓,并利用鏡像對(duì)稱(chēng)原理求取二維輪廓的三維信息。林家賢[5]等通過(guò)編碼器—解碼器網(wǎng)絡(luò)結(jié)構(gòu)生成了花朵不同視角下的RGB圖和深度圖。何振邦等[6]對(duì)用戶(hù)手繪信息進(jìn)行預(yù)處理和分析,并結(jié)合植物學(xué)知識(shí)來(lái)恢復(fù)花朵的深度信息。殷悅等[7]采用SURF特征檢測(cè)算法和SIFT特征匹配算法將植物的二維數(shù)據(jù)轉(zhuǎn)化為三維坐標(biāo),從而得到逼真的三維植物模型。婁路等[8]采用深度卷積神經(jīng)網(wǎng)絡(luò)Mask-RCNN對(duì)植物莖葉進(jìn)行分割并提取其特征。綜上,基于圖像的花朵建模以圖像信息為出發(fā)點(diǎn),不僅獲取途徑多樣,而且可以捕捉到物體的真實(shí)形態(tài)。

本文首先以二維圖像為基礎(chǔ),根據(jù)正投影原理和鏡像對(duì)稱(chēng)原理,將花朵擬合為一個(gè)三維圓錐,求取二維圖像缺失的三維深度數(shù)據(jù),建立一個(gè)具有真實(shí)感的三維模型;其次在用戶(hù)繪制的二維橢圓基礎(chǔ)上,采用變換矩陣,將三維模型根據(jù)二維橢圓進(jìn)行相應(yīng)的變換,形成多角度的模型;最后生成針織意匠圖并織成相應(yīng)的織物。通過(guò)三維模型生成的針織意匠圖,不僅提高了工作效率,而且用戶(hù)可以根據(jù)自己的需求,調(diào)整模型的角度,生成多個(gè)針織圖案。

1 基于二維圖像的花卉三維模型建立

通過(guò)分析二維圖像中花朵的結(jié)構(gòu),將花朵擬合為一個(gè)具有一定傾斜度的三維圓錐來(lái)粗略估計(jì)花的幾何形狀及方向,假設(shè)圓錐體的頂端位于花的中心,花瓣大致位于圓錐體的表面,以此來(lái)求得花朵的深度信息。

1.1 用戶(hù)交互

本文以一個(gè)六瓣花朵的花卉為例,在花朵建模之前,用戶(hù)交互式描繪出二維圖像中每個(gè)花瓣的兩條輪廓曲線(xiàn)CL和CR,若第一條曲線(xiàn)CL的采樣點(diǎn)總數(shù)為10,則按照{(diào)P1,P1L,1,P1L,2,…,P1L,8,E1}的順序保存這條曲線(xiàn)上的離散采樣點(diǎn),如圖1(a)所示。后期需要將每個(gè)花瓣的一對(duì)對(duì)稱(chēng)二維曲線(xiàn)進(jìn)行三維深度值的恢復(fù),如圖1(b)所示。將每個(gè)花瓣的兩條邊緣曲線(xiàn)的共同起點(diǎn)設(shè)為P1、P2、P3、P4、P5、P6,存放入一個(gè)集合V1,再將兩條邊緣曲線(xiàn)的終點(diǎn)E1、E2、E3、…、E12存入另一個(gè)集合V2中。利用最小二乘法[9]將集合V1中的數(shù)據(jù)擬合出一個(gè)橢圓e1,其圓心為O1,該橢圓即為后期擬合出的三維圓錐底面圓在XOY平面上所得的投影。將V2中的數(shù)據(jù)采用同樣的方法擬合出橢圓e2,則e2的圓心視為二維圖像中花朵的花心,也是三維圓錐的頂點(diǎn)O2(圖1(c))。

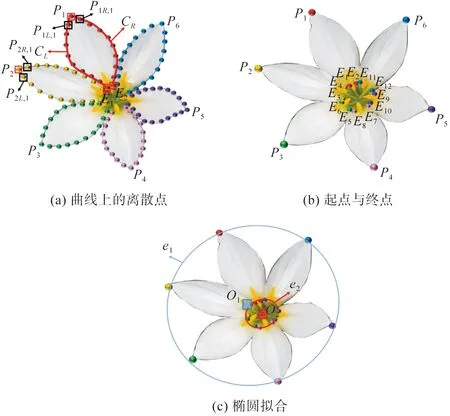
圖1 采樣點(diǎn)與橢圓擬合

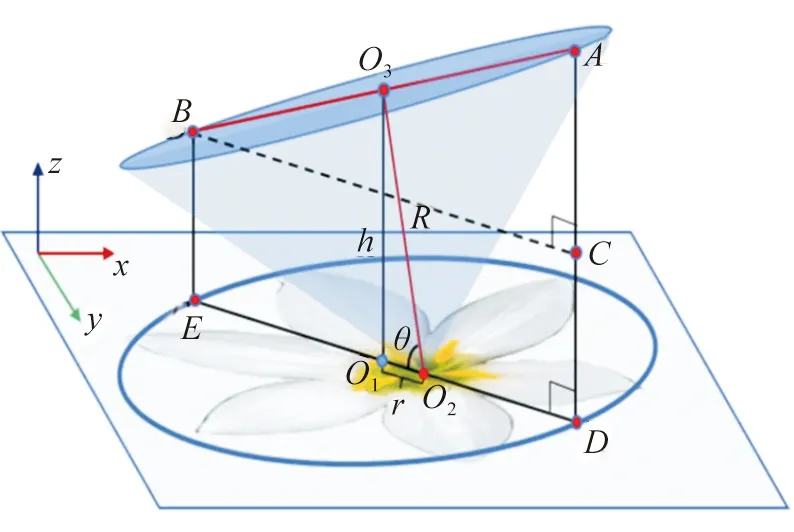
圖2 擬合圓錐

1.2 擬合三維圓錐

假定花朵模型為一個(gè)具有一定傾斜度的三維圓錐,并將上一步驟中由花瓣起點(diǎn)擬合得到的橢圓e1視為圓錐經(jīng)過(guò)平行投影得到的圖形,如圖2所示。橢圓e1的圓心為O1,該點(diǎn)也是三維圓錐底面圓的圓心O3在XOY面上的投影點(diǎn),由該橢圓也可得到其長(zhǎng)短軸a和b。由正投影原理可知,線(xiàn)段AB在XOY平面上的投影線(xiàn)為DE,并且圖2中三角形ABC與三角形O2O3O1相似,因此可以求得三維圓錐的高R與O2O1之間的長(zhǎng)度r的比值,如下式所示:

(1)

式中:AB為圓錐底面直徑,長(zhǎng)度等于橢圓e1的長(zhǎng)軸a,BC長(zhǎng)度等于橢圓e1的短軸b。

根據(jù)式(1)可以求出R,而三角形O2O3O1為直角三角形,因此也可求出圓錐的傾斜角度θ及圓錐底面圓心O3到XOY平面的垂直高度h。

1.3 求花瓣三維深度

1.3.1 求對(duì)稱(chēng)面法向量

絕大多數(shù)的花朵在結(jié)構(gòu)中會(huì)表現(xiàn)出一定的對(duì)稱(chēng)性,主要表現(xiàn)為兩側(cè)對(duì)稱(chēng)和輻射對(duì)稱(chēng)兩種方式[10]。將花朵的花瓣視為一個(gè)對(duì)稱(chēng)的物體,將二維圖片中每個(gè)花瓣的起點(diǎn)Pi在三維空間中對(duì)應(yīng)的點(diǎn)pi與圓錐底面圓心O3及花心O2組成的平面設(shè)為每個(gè)立體花瓣的對(duì)稱(chēng)面,如圖3所示。

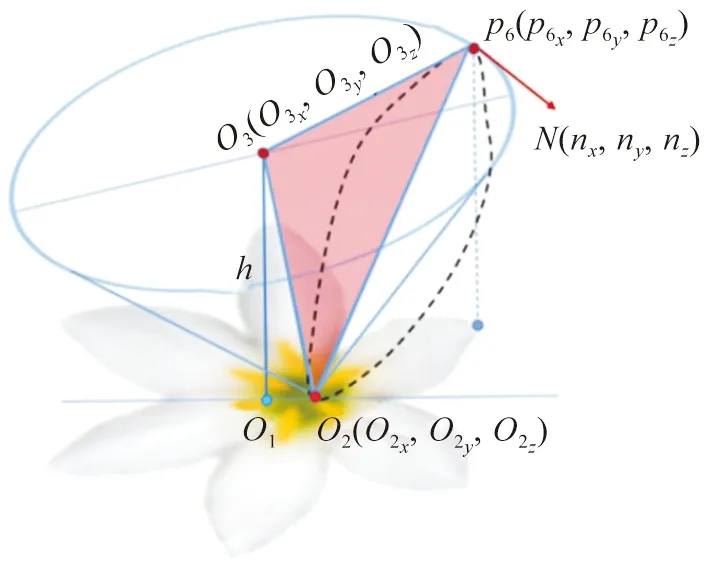
圖3 對(duì)稱(chēng)面和法向量

本文以第六片花瓣為例,其對(duì)稱(chēng)面為p6、O3、O2,設(shè)N為其對(duì)稱(chēng)面的法向量。由于點(diǎn)O2和O1都在XOY平面上,且O1為O3在XOY面上的投影點(diǎn),可知點(diǎn)O3的z坐標(biāo)值是點(diǎn)O2的z坐標(biāo)值與高度h的和。另外,由于點(diǎn)O2、O3、p6的x坐標(biāo)和y坐標(biāo)已知,O3、p6的z坐標(biāo)之差可由下式推導(dǎo)得出:

O3z-p6z=[(O3x-O2x)·(O3x-p6x)+(O3y-O2y)·(O3y-p6y)]/(-h)

(2)

因此該對(duì)稱(chēng)面的法向量N可由向量O2O3和p6O3叉乘求得。求出法向量N后,后續(xù)即可根據(jù)該法向量及二維圖形中的一對(duì)對(duì)稱(chēng)點(diǎn)坐標(biāo),并結(jié)合鏡像對(duì)稱(chēng)原理求得對(duì)稱(chēng)點(diǎn)的三維深度信息。

1.3.2 求三維深度

求出每個(gè)花瓣的對(duì)稱(chēng)面及相應(yīng)的法向量后,即可求得兩條對(duì)稱(chēng)曲線(xiàn)中每對(duì)對(duì)稱(chēng)點(diǎn)的三維深度,如圖4所示。

圖4 根據(jù)鏡像對(duì)稱(chēng)求深度值

根據(jù)關(guān)于鏡面對(duì)稱(chēng)的兩個(gè)特性,1) 兩點(diǎn)連線(xiàn)垂直于對(duì)稱(chēng)面,且兩點(diǎn)到對(duì)稱(chēng)面的距離相等;2) 兩點(diǎn)的垂直平分線(xiàn)垂直于對(duì)稱(chēng)面的法向量[9],可得:

(p6R,3+p6L,3)·N=0

(3)

(p6R,3-p6L,3)·N⊥=0

(4)

式中:p6L,3和p6R,3為三維空間中的一對(duì)對(duì)稱(chēng)點(diǎn),N為這兩點(diǎn)鏡像對(duì)稱(chēng)的對(duì)稱(chēng)面的法向量,N⊥為垂直于N的某一向量。

設(shè)p6L,3=(x1,y1,z1),p6R,3=(x2,y2,z2),N=(nx,ny,nz),N⊥=(-nz,0,nx),代入下式,可計(jì)算出p6L,3和p6R,3的z坐標(biāo):

(5)

(6)

將每對(duì)對(duì)稱(chēng)點(diǎn)代入式(5)(6),即可計(jì)算得到每?jī)蓷l對(duì)稱(chēng)曲線(xiàn)上對(duì)稱(chēng)點(diǎn)的三維深度,從而可以得到每個(gè)花瓣的邊緣曲線(xiàn)深度。

1.3.3 生成花瓣曲面

獲得花瓣的三維邊緣點(diǎn)之后,還需要生成花瓣曲面。由于花瓣并不是扁平的,花瓣中心具有一定的內(nèi)凹趨勢(shì),本文將花瓣的凹陷程度視為與之橫向長(zhǎng)度對(duì)應(yīng)的正弦函數(shù)。將每個(gè)花瓣中的兩條三維邊緣曲線(xiàn)重新采樣,兩兩相對(duì)的采樣點(diǎn)組成一對(duì)對(duì)稱(chēng)點(diǎn),進(jìn)行橫向的均勻插值,將這些插值點(diǎn)作為初步的花瓣網(wǎng)格模型頂點(diǎn),如圖5所示。

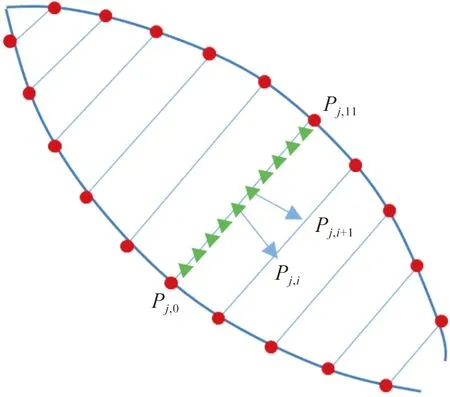
圖5 每對(duì)對(duì)稱(chēng)點(diǎn)之間進(jìn)行橫向均勻插值

本文改進(jìn)了濮群等[11]在二維平面中計(jì)算花朵內(nèi)凹趨勢(shì)的研究方法,直接在三維空間中將三角函數(shù)在一個(gè)周期內(nèi)的彎曲特性作為花瓣曲面中三維點(diǎn)的內(nèi)凹趨勢(shì),如圖6所示。

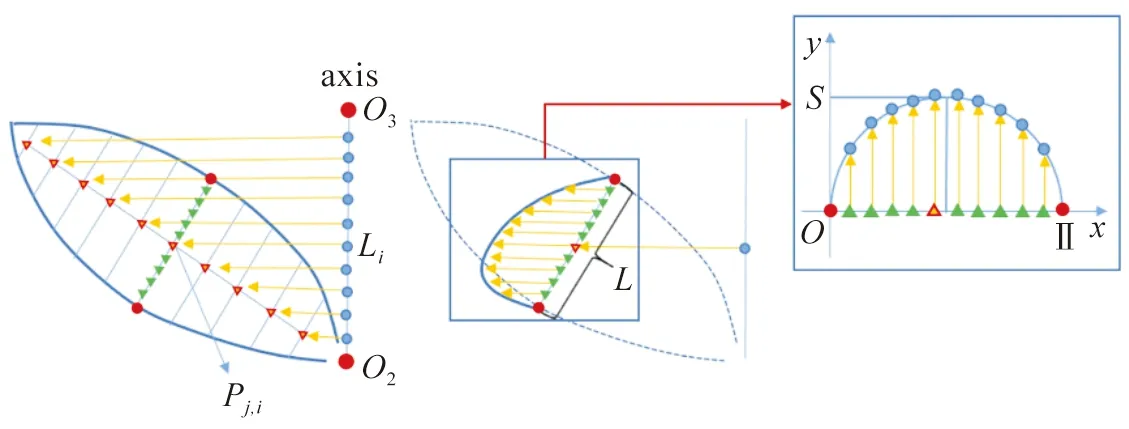
圖6 橫向采樣點(diǎn)移動(dòng)的方向和距離

首先計(jì)算出每對(duì)對(duì)稱(chēng)點(diǎn)之間的長(zhǎng)度L,依據(jù)先驗(yàn)知識(shí),蔥蘭花花瓣的內(nèi)凹趨勢(shì)并不明顯,因此可以將正弦函數(shù)的振幅S設(shè)為L(zhǎng)的20%～40%。將三角函數(shù)的周期t設(shè)為橫向采樣點(diǎn)的總個(gè)數(shù),計(jì)算如下式所示:

(7)

式中:i為橫向綠色三角形插值點(diǎn)的索引號(hào)。

對(duì)三維圓錐底面圓心O3和花心O2所連線(xiàn)段axis進(jìn)行采樣,該線(xiàn)段上的采樣點(diǎn)數(shù)目與三維邊緣曲線(xiàn)上的采樣點(diǎn)數(shù)目相等,如圖6所示。選取每條橫向采樣點(diǎn)點(diǎn)集中的中點(diǎn)Pj,i,將其與axis上對(duì)應(yīng)的藍(lán)色采樣點(diǎn)Li進(jìn)行連接,該向量即為橫向采樣點(diǎn)需要移動(dòng)的方向。每個(gè)橫向采樣點(diǎn)移動(dòng)的距離即為式(7)中對(duì)應(yīng)的y值。橫向采樣點(diǎn)移動(dòng)到新的位置后,將新的橫向采樣點(diǎn)按照Pj,i+1、Pj,i、Pj+1,i的順序依次連接,形成三角面片;然后再按Pj+1,i+1、Pj,i+1、Pj+1,i的順序?qū)⑷敲嫫a(bǔ)齊,形成完整的花瓣曲面,如圖7所示。

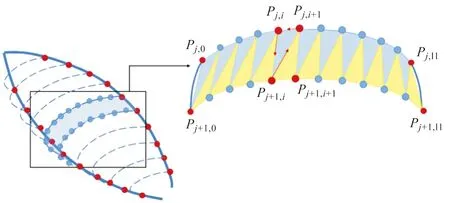
圖7 三角面片和花瓣曲面的生成

按照上述順序在花瓣的每?jī)山M對(duì)稱(chēng)點(diǎn)之間橫向插值,再依次生成三角面片,從而形成完整的花瓣模型。圖8為最終形成的三維花朵模型。

圖8 花朵模型

2 三維模型的空間變換

考慮到花瓣頂點(diǎn)構(gòu)成的圓在平面上的投影近似橢圓,本文制作了一個(gè)可供用戶(hù)繪制橢圓的界面。在該界面,用戶(hù)可通過(guò)鼠標(biāo)操作來(lái)控制橢圓的大小及位置,并且可以通過(guò)此二維橢圓來(lái)改變花朵形態(tài),從而生成多種角度的二維圖案。

2.1 橢圓繪制界面的制作

利用MFC制作一個(gè)可供用戶(hù)通過(guò)鼠標(biāo)操作來(lái)繪制橢圓的界面,如圖9所示。用戶(hù)首先通過(guò)鼠標(biāo)點(diǎn)擊來(lái)確定橢圓的中心位置C,確定橢圓位置后會(huì)自動(dòng)生成兩個(gè)坐標(biāo)點(diǎn)A和B。移動(dòng)A點(diǎn)和B點(diǎn)可以調(diào)整橢圓長(zhǎng)半軸a和短半軸b的具體長(zhǎng)度,從而通過(guò)改變橢圓的大小及傾斜度來(lái)改變花朵模型。

圖9 二維橢圓和三維模型

將(0,0)點(diǎn)設(shè)為視口的左下角坐標(biāo),將屏幕的長(zhǎng)cx和寬cy設(shè)為視口的右上角坐標(biāo)。根據(jù)A、B點(diǎn)及橢圓圓心C點(diǎn)在繪制橢圓界面上的像素坐標(biāo)點(diǎn),按式來(lái)計(jì)算A、B、C三點(diǎn)在屏幕中顯示的新坐標(biāo)點(diǎn)A′、B′、C′。

(8)

式中:i為A、B、C三點(diǎn)的索引號(hào)。

圖9為初始模型根據(jù)二維橢圓變換后的最終效果,即選取了三種不同大小及傾斜程度的橢圓進(jìn)行實(shí)驗(yàn),結(jié)果表明模型變換效果良好。圖9(a)為繪制界面中三種不同形狀的橢圓,圖9(b)為兩種花卉三維模型根據(jù)橢圓信息變換后的效果。

2.2 三維模型位置的初步調(diào)整

將本文中建立的花朵模型視為一個(gè)規(guī)則的三維圓錐,因此可以將每個(gè)花瓣的頂點(diǎn)所圍成的圖形視為一個(gè)規(guī)則的圓形,將該圓形的圓心O3與圓錐頂點(diǎn)O2的連線(xiàn)視為圓錐的中軸,如圖10所示。首先將該圓形平面平移,使得圓心O3與原點(diǎn)(0,0,0)重合,將向量O3O2歸一化,再將圓錐根據(jù)下式經(jīng)過(guò)旋轉(zhuǎn)變換,使其與Z軸平行。

z=(0,0,-1)

(9)

NR=O3O2×z

(10)

cosσ=O3O2·z

(11)

式中:NR為三維模型進(jìn)行初步旋轉(zhuǎn)的旋轉(zhuǎn)軸,σ為旋轉(zhuǎn)角度。

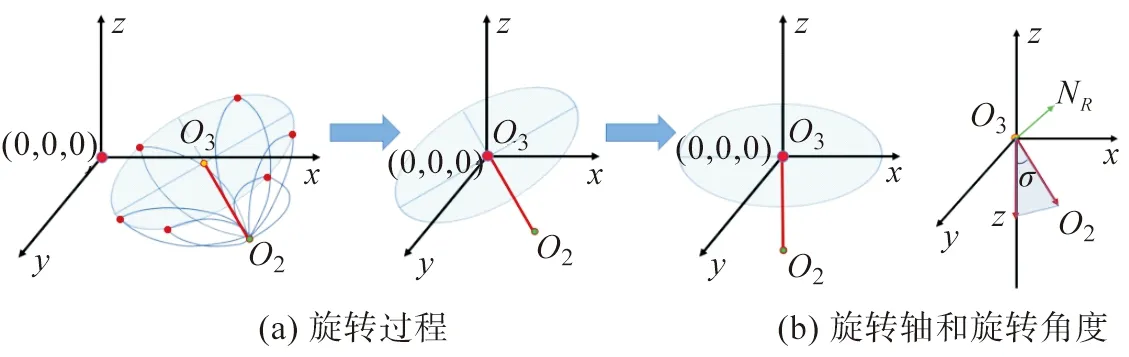
圖10 模型的初步變換

2.3 基于橢圓信息的模型變換

初步變換后的圓錐中軸O3O2與Z軸平行且底面圓心與原點(diǎn)重合,因此可將圓錐的底面圓所在平面視為用戶(hù)繪制橢圓的界面。底面經(jīng)過(guò)一定旋轉(zhuǎn),在XOY平面上的正交投影可變?yōu)榕c用戶(hù)繪制橢圓相近的形狀,如圖11(沿Z軸方向看,也可稱(chēng)為俯視圖)所示。首先根據(jù)A′、B′及橢圓圓心C′的坐標(biāo)計(jì)算出橢圓的長(zhǎng)半軸a與短半軸b,以及橢圓長(zhǎng)半軸a與圓半徑k的比值m。利用縮放矩陣,將模型沿著X軸、Y軸、Z軸同時(shí)縮放m倍。經(jīng)過(guò)縮放后的花朵模型中,花瓣頂點(diǎn)擬合出的圓形,其半徑與繪制橢圓的長(zhǎng)半軸大小相等。

(12)

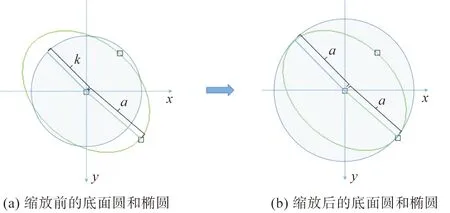
圖11 縮放模型

假設(shè)空間坐標(biāo)系水平向右為X軸正方向,垂直屏幕指向用戶(hù)為Z軸負(fù)方向,垂直向上為Y軸正方向。在XOY平面上的具有同樣大小和傾斜角度的橢圓,可以由中軸與Z軸平行的三維圓錐經(jīng)過(guò)4種不同的旋轉(zhuǎn)方式近似得到。本文以圖11中的橢圓為例,圓錐可按以下4種方式旋轉(zhuǎn):1) 若三維圓錐的中軸O3O2指向Z軸的正方向,將圓錐沿A′C′所在軸線(xiàn)順時(shí)針旋轉(zhuǎn)一定角度β,可得一中軸指向右上方的三維圓錐。2) 若三維圓錐的中軸O3O2指向Z軸的正方向,將圓錐沿A′C′所在軸線(xiàn)逆時(shí)針旋轉(zhuǎn)一定角度β,可得一中軸指向左上方的三維圓錐。3) 若三維圓錐的中軸O3O2指向Z軸的負(fù)方向,將圓錐沿A′C′所在軸線(xiàn)順時(shí)針旋轉(zhuǎn)一定角度β,可得一中軸指向左下方的三維圓錐。4) 若三維圓錐的中軸O3O2指向Z軸的負(fù)方向,將圓錐沿A′C′所在軸線(xiàn)逆時(shí)針旋轉(zhuǎn)一定角度β,可得一中軸指向右下方的三維圓錐。而在前文三維模型的初步變換中,選取的三維向量z(0,0,-1)指向Z軸的負(fù)方向,因此選擇第三種旋轉(zhuǎn)方式,如圖12所示。

圖12 旋轉(zhuǎn)模型

將縮放過(guò)后的模型沿著A′C′所在軸線(xiàn)進(jìn)行順時(shí)針旋轉(zhuǎn),旋轉(zhuǎn)角度為β,如圖12(b)所示。根據(jù)式(13～16)可計(jì)算出模型的旋轉(zhuǎn)軸L及旋轉(zhuǎn)角β。其中,由于旋轉(zhuǎn)軸L在XOY平面上,因此其z坐標(biāo)值為0。利用旋轉(zhuǎn)矩陣,將模型的每個(gè)三維點(diǎn)進(jìn)行旋轉(zhuǎn),旋轉(zhuǎn)后的三維花朵模型,花瓣頂點(diǎn)擬合出的圓在XOY平面上的正交投影形狀大致與用戶(hù)繪制的橢圓相近。

(13)

(14)

(15)

(16)

若在繪制界面中存在多個(gè)橢圓,且每個(gè)橢圓的大小及傾斜角度不一,需要將每個(gè)三維模型在原點(diǎn)經(jīng)過(guò)縮放、旋轉(zhuǎn)變換后,移動(dòng)到橢圓圓心即C′的坐標(biāo)位置,形成最終圖案。利用平移矩陣,再將模型的每個(gè)三維點(diǎn)進(jìn)行平移,如圖13所示。

圖13 平移模型

模型經(jīng)過(guò)上述三個(gè)步驟之后,就可以轉(zhuǎn)變?yōu)榕c二維橢圓大小、方向一致的三維模型。

(17)

3 生成針織意匠圖并上機(jī)織造

3.1 生成意匠圖

將繪制的橢圓圖案以三維模型代替后,由于每一朵三維花朵方向大小不同,與光源的相對(duì)位置不同,渲染后每朵花的明暗亦不同,渲染后為24位真彩色,而提花織物常用2色、3色提花,一般不超過(guò)5色,因此需要使用減色算法[12]將其減為合適的顏色數(shù)。

減色后的圖案由黑、白、灰三種顏色組成,對(duì)應(yīng)提花圖案中三種不同的層次,其中白色作為圖案的背景色,灰色作為過(guò)渡色,黑色作為花朵上邊緣處最深的陰影色。為了讓生成的意匠圖更具立體感,本文將圖案中占有較大面積且隨機(jī)分布的灰色進(jìn)行組織填充,填充為一隔一的過(guò)渡色,從而形成具有漸變效果的意匠圖(圖14)。圖14(a)為繪制的二維橢圓圖案,圖14(b)為根據(jù)橢圓生成的三維模型,圖14(c)為最終生成的意匠圖,其中上部的放大圖表示一隔一過(guò)渡色區(qū)域,下部的放大圖表示花朵邊緣最深的陰影色,即純黑色區(qū)域。

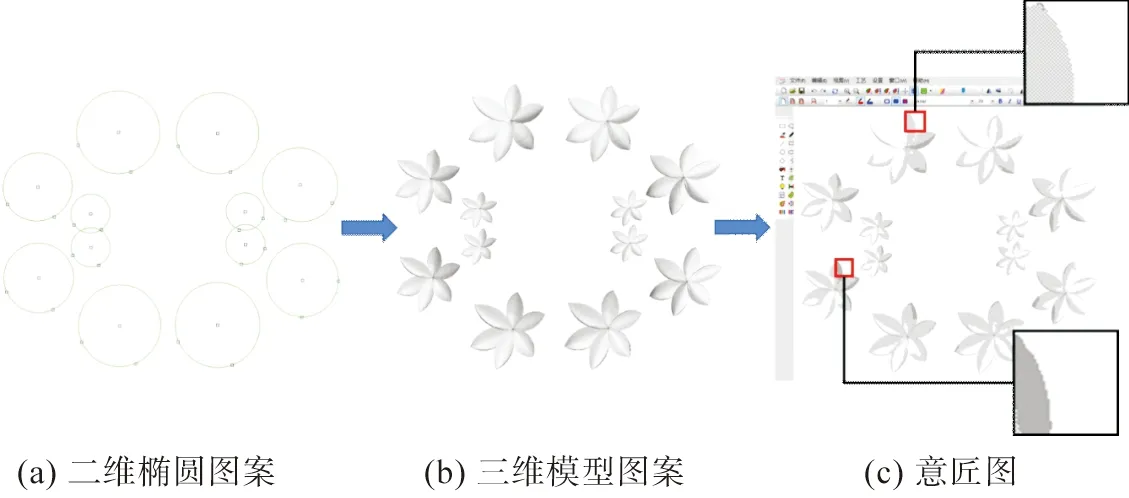
圖14 從模型到意匠圖的實(shí)現(xiàn)步驟

3.2 工藝反面設(shè)計(jì)和上機(jī)實(shí)驗(yàn)

經(jīng)過(guò)填色的花型意匠圖表示的是織物正面線(xiàn)圈形成的圖案,還不能直接用于生產(chǎn),這是因?yàn)樘峄椢锏墓に嚪疵婵椢锟赡艽嬖谳^長(zhǎng)的浮線(xiàn)。長(zhǎng)浮線(xiàn)會(huì)影響編織的連續(xù)進(jìn)行,并且在織物使用過(guò)程中浮線(xiàn)容易被勾斷從而縮短生命期限。為克服這一缺陷,在設(shè)計(jì)時(shí)可以在長(zhǎng)浮線(xiàn)區(qū)域間隔地配置成圈或集圈,讓浮線(xiàn)長(zhǎng)度變短。成圈組織會(huì)形成完整線(xiàn)圈,破壞正面提花效果,不是理想的選擇。集圈組織不會(huì)單獨(dú)形成完整線(xiàn)圈,其紗線(xiàn)懸掛在其他線(xiàn)圈的后面,因而不易在織物提花面顯露,是縮短浮線(xiàn)常用的方式。因此本文實(shí)驗(yàn)選擇在長(zhǎng)浮線(xiàn)區(qū)域間隔配置集圈組織。

集圈組織點(diǎn)一般在編織意匠圖上配置,編織意匠圖的高度為花型意匠圖高度和色紗數(shù)的乘積。集圈的排列方式和數(shù)量會(huì)關(guān)系到紗線(xiàn)的消耗、織物平方米質(zhì)量、延伸性等,需要合理配置。一般可以沿縱行方向和斜向配置集圈點(diǎn),其中斜向配置更加常見(jiàn)。對(duì)一般提花織物,將浮線(xiàn)長(zhǎng)度控制在3～4針即可有效減少鉤絲現(xiàn)象。實(shí)驗(yàn)使用的花型意匠圖上有大片的白色背景,該區(qū)域在織物反面相鄰路上的黑色紗線(xiàn)形成長(zhǎng)浮線(xiàn)。在每一路上隔3個(gè)浮線(xiàn)組織點(diǎn)配置一個(gè)集圈點(diǎn),并將集圈點(diǎn)逐路向右移動(dòng)一針。體現(xiàn)在織物上,上一橫列黑紗集圈點(diǎn)正好在下一橫列兩個(gè)黑紗集圈的中間,兩邊對(duì)稱(chēng),集圈點(diǎn)分布均勻,織物平整,如圖15(e)右側(cè)的局部放大圖所示。添加完集圈組織點(diǎn)的意匠圖即可導(dǎo)出上機(jī)文件在圓機(jī)上編織。

本文選取兩種不同的花型進(jìn)行模型的建立及實(shí)驗(yàn)編織,編織效果如圖15所示,織物的圖案清晰且具有一定立體感。圖15(a)為兩種花卉原始圖片,圖15(b)為兩種花卉對(duì)應(yīng)的意匠圖,圖15(c)為上機(jī)編織出的圓筒狀實(shí)物圖,圖15(d)為最終的兩款織物實(shí)物圖,圖15(e)左側(cè)圖為(d)中左側(cè)花卉的局部花瓣放大圖。

圖15 從意匠圖到織物的實(shí)現(xiàn)步驟

4 結(jié) 論

本文提出了一種基于三維數(shù)據(jù)的針織意匠圖生成算法。根據(jù)花朵的結(jié)構(gòu)特征,建立了基于正投影原理和鏡像對(duì)稱(chēng)原理的花朵三維模型;通過(guò)用戶(hù)繪制的二維橢圓,對(duì)已有模型進(jìn)行變換處理,生成了多角度的花朵三維模型;最后將三維模型生成圖案,轉(zhuǎn)換為提花圓機(jī)可用的花型意匠圖,并且在提花緯編機(jī)上織成了實(shí)物。本文提出的算法能夠在較短時(shí)間內(nèi)完成對(duì)花朵的模型建立,實(shí)現(xiàn)意匠圖的快速生成和上機(jī)使用,提高了工作效率,并且建立的模型可以重復(fù)利用,易于產(chǎn)品系列化設(shè)計(jì)的實(shí)現(xiàn)。

《絲綢》官網(wǎng)下載

中國(guó)知網(wǎng)下載