永磁同步電機模型預測轉矩控制客觀評價法綜述*

李耀華, 張鑫泉, 鄧益志, 童瑞齊, 劉晶郁

(長安大學 汽車學院,陜西 西安 710064)

0 引 言

永磁同步電機(PMSM)模型預測轉矩控制(MPTC)通過成本函數直接控制磁鏈和轉矩,選擇令成本函數最小的開關狀態作為下一時刻的輸出,受到了廣泛關注[1-5]。作為控制系統的核心,磁鏈和轉矩的重要性相當,但二者的量綱和數量級不同。因此,需要采用加權求和形式的成本函數,而權重系數設計和調整較為困難,尚無理論化的解決途徑[6-7]。權重系數可通過試驗法得到,但此方法需進行大量前期試驗。當控制變量和考慮影響因素增多,試驗次數呈指數型上升[8-9]。

為解決這一問題,文獻[10-13]采用模糊控制動態調節權重系數,但模糊規則的設定具有一定的主觀性,依靠設計者的先驗知識。文獻[14-15]采用粒子群算法和神經網絡算法調整權重系數,但需要構造大量訓練數據集且算法自身計算量較大。文獻[16]將磁鏈和轉矩轉換為相對誤差率,但如果含控制目標的參考值不確定,如:開關次數,仍需設計權重系數。文獻[17-18]對各控制變量獨立排序,成本函數為無量綱的排序位置,但排序計算量較大。文獻[19-20]將多目標成本函數加權求和形式轉換為單目標成本函數級聯形式,從而消除權重系數。

模型預測轉矩控制根據磁鏈和轉矩控制效果,從備選電壓矢量集合中選擇最優電壓矢量,本質屬于多目標最優決策方法。客觀評價法根據原始數據之間的關系通過一定的數學方法來選擇最優候選對象,結果不依賴于設計者的主觀判斷,可應用于多目標決策。本文將客觀評價法中的模糊決策法、VIKOR法、TOPSIS法、變異系數賦權法和熵值賦權法引入永磁同步電機模型預測轉矩控制中,通過仿真,驗證客觀評價法的可行性。

1 永磁同步電機模型預測轉矩控制

定子坐標系下,表貼式永磁同步電機定子磁鏈矢量與轉矩預測模型如式(1)和式(2)所示:

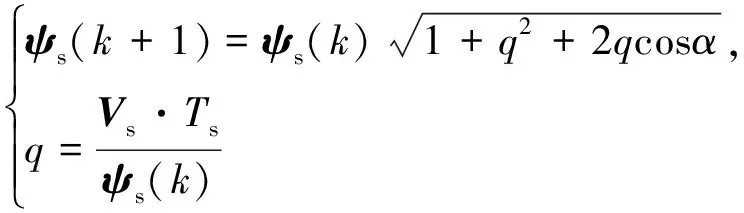
(1)

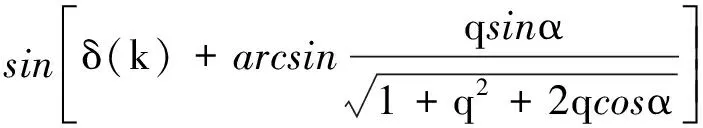
(2)

式中:ψs(k)、δ(k)和Te(k)分別為k時刻的定子磁鏈矢量、轉矩角和電磁轉矩;ψs(k+1)、δ(k+1)和Te(k+1)分別為k+1時刻的定子磁鏈矢量、轉矩角和電磁轉矩;Vs和α分別為施加電壓矢量幅值和施加電壓矢量與定子磁鏈的夾角[14];ψf為轉子永磁體磁鏈;p為電機極對數;Ld為電機d軸電感。

兩電平三相逆變器可產生7個備選電壓矢量,如式(3)所示,其中零電壓矢量可由開關狀態000或111生成,具體選擇遵循開關次數最小原則。

Vs∈{V0,V1,V2,V3,V4,V5,V6}

(3)

定義模型預測轉矩控制成本函數如式(4)所示:

g=gTe+λgψs

(4)

式中:λ為權重系數;gTe和gψs分別為轉矩控制項和磁鏈控制項。

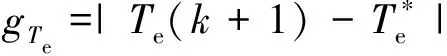
(5)

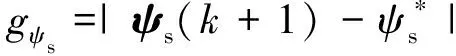
(6)

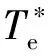
永磁同步電機模型預測轉矩系統框圖如圖1所示。

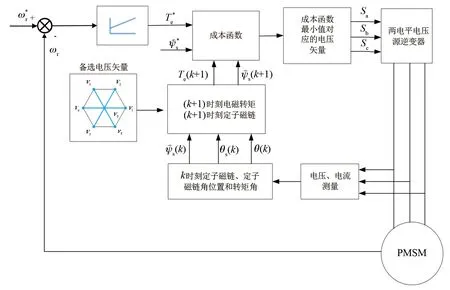
圖1 永磁同步電機模型預測轉矩系統

在MATLAB/Simulink中建立基于定子坐標系的表貼式永磁同步電機模型預測轉矩控制仿真模型。該仿真模型為離散模型,采樣時間為5×10-5s。參考轉速初始為500 r/min,2 s時階躍至-500 r/min;負載轉矩初始為10 N·m,1 s時階躍至-10 N·m,3 s時階躍至10 N·m。仿真總時長為4 s。仿真參數如表1所示。經試驗法確定權重系數λ=100,電機系統仿真波形如圖2～5所示。

表1 仿真系統參數

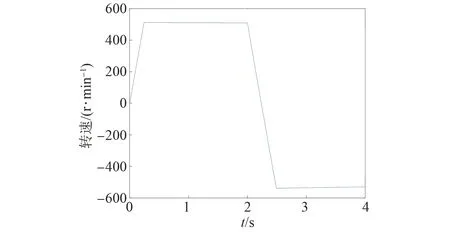
圖2 權重系數λ=100下的電機轉速

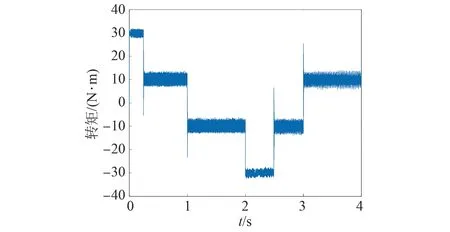
圖3 權重系數λ=100下的電機轉矩

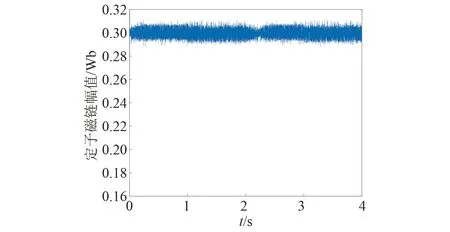
圖4 權重系數λ=100下的定子磁鏈幅值

轉矩脈動均方根誤差(RMSE)、磁鏈脈動均方根誤差和平均開關頻率的定義如式(7)～式(9)所示:

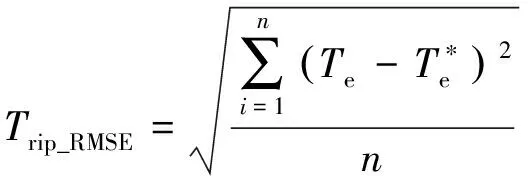
(7)

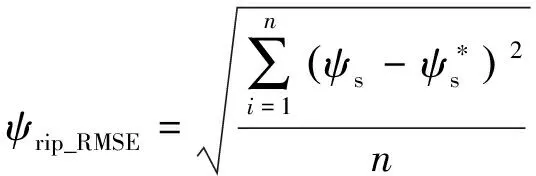
(8)

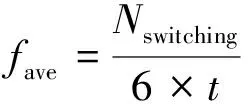
(9)

式中:n為采樣個數;Nswitching為逆變器上下橋臂開關總次數;t為仿真總時長。

永磁同步電機模型預測轉矩控制系統性能如表2所示。

表2 永磁同步電機模型預測轉矩控制系統性能

表3 基于模糊決策法的系統性能

2 基于客觀評價法模型預測轉矩控制

客觀評價法需要統一控制變量的數量級,將轉矩控制和磁鏈控制的成本函數標幺化,統一在[0,1]之間,如式(10)和(11)所示[21]:

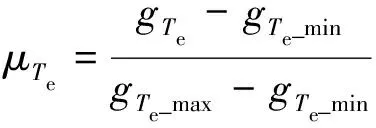
(10)

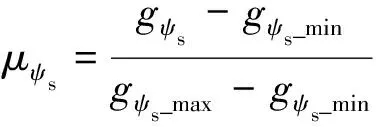
(11)

基于標幺化的成本函數如式(12)所示:

g=μTe+μψs

(12)

2.1 模糊決策法

模糊決策法采用模糊數學對目標模糊的對象系統進行定量決策,可應用于模型預測控制[22-23]。

采用最大隸屬度算子對標幺化的成本函數模糊化,如式(13)所示。下一時刻選擇電壓矢量為μD最小值對應的電壓矢量,如式(14)所示:

μD=max(μTe,μψs)

(13)

Vopt=arg minμD

(14)

基于模糊決策法的永磁同步電機模型預測轉矩控制仿真波形如圖5～7所示,控制性能如表4所示。

表4 基于VIKOR法的系統性能

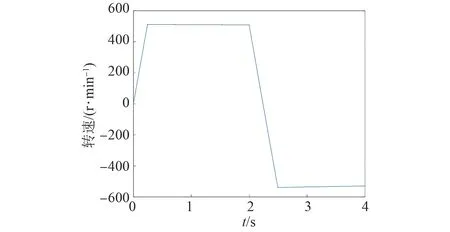
圖5 基于模糊決策法的電機轉速

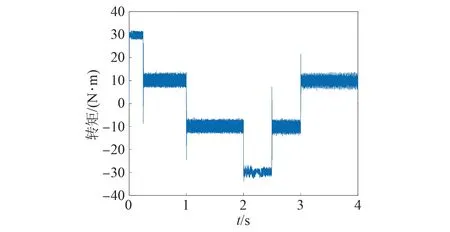
圖6 基于模糊決策法的電機轉矩

圖7 基于模糊決策法的電機定子磁鏈幅值

2.2 基于VIKOR法

多準則妥協解排序法(VIKOR)是一種多目標決策方法,其根據評估值與理想值的接近程度對排列優先順序進行客觀評價,可用于模型預測控制[24]。

基于VIKOR法的永磁同步電機模型預測轉矩控制算法步驟如下。

步驟一,確定標幺化的轉矩控制成本函數和磁鏈控制成本函數的群體效用值S與個體遺憾值R,如式(15)和式(16)所示:

S=0.5μTe+0.5μψs

(15)

R=max(0.5μTe,0.5μψs)

(16)

步驟二,計算折衷決策指標值Q,如式(17)所示:

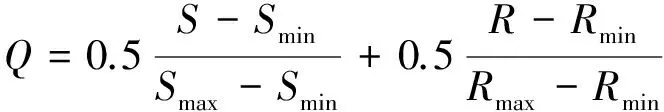
(17)

步驟三,選擇對應折衷決策指標值最小的電壓矢量作為輸出,如式(18)所示:

Vopt=arg minQ

(18)

基于VIKOR法的永磁同步電機模型預測轉矩控制仿真波形如圖8～10所示,控制性能如表4所示。

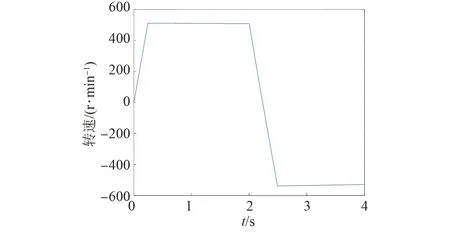
圖8 基于VIKOR法的電機轉速

圖9 基于VIKOR法的電機轉矩

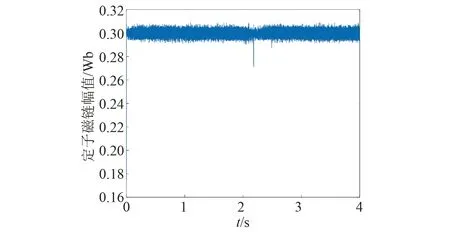
圖10 基于VIKOR法的電機定子磁鏈幅值

2.3 基于TOPSIS法

優劣解距離法(TOPSIS)是根據評價對象與理想目標的接近程度進行相對優劣評價的一種綜合評價方法,可用于模型預測控制[25]。

基于TOPSIS法的永磁同步電機模型預測轉矩控制算法步驟如下。

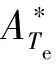
步驟二,計算備選狀態與最優解和最劣解之間的差距,如式(19)和(20)所示:

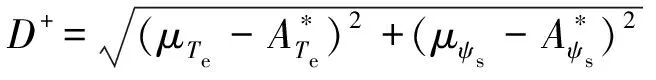
(19)

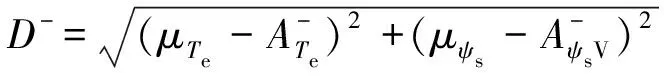
(20)

步驟三,計算接近系數,如式(21)所示:

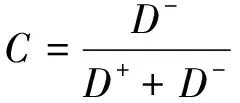
(21)

步驟四,選擇對應接近系數最大的電壓矢量作為輸出電壓矢量,如式(22)所示:

Vopt=arg maxC

(22)

基于TOPSIS法的永磁同步電機模型預測轉矩控制仿真波形如圖11～13所示,控制性能如表5所示。

表5 基于TOPSIS法的系統性能

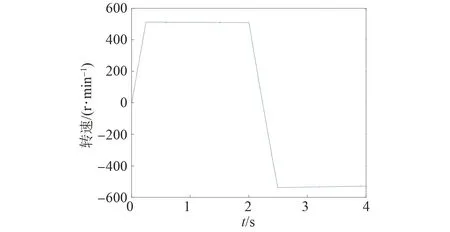
圖11 基于TOPSIS法的電機轉速

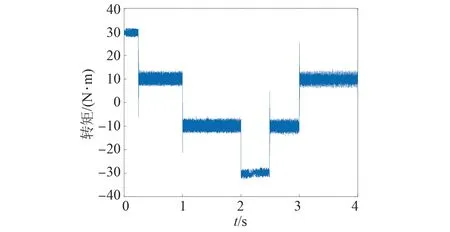
圖12 基于TOPSIS法的電機轉矩

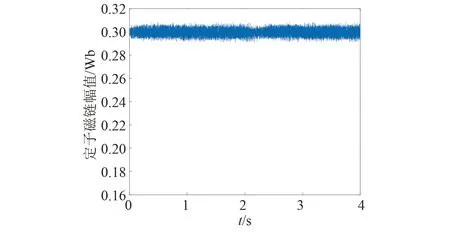
圖13 基于TOPSIS法的電機定子磁鏈幅值

2.4 基于變異系數賦權法

變異系數法是根據各項指標的信息計算得到離散程度與權重的客觀賦權方法,可用于模型預測控制權重系數的設計[26]。

基于變異系數賦權法的永磁同步電機模型預測轉矩控制算法步驟如下。

步驟一,計算標幺化后的轉矩控制和磁鏈控制成本函數的平均值和標準差,如式(23)～式(26)所示:

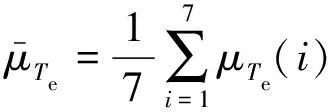
(23)

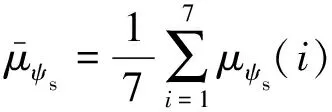
(24)

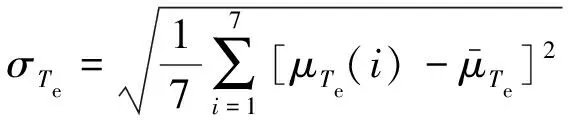
(25)

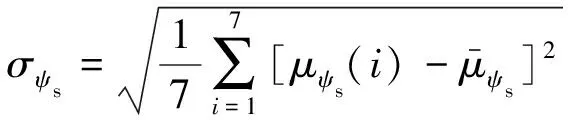
(26)

步驟二,根據平均值和標準差,計算變異系數,如式(27)和(28)所示:

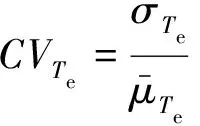
(27)

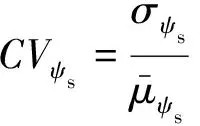
(28)

步驟三,得到基于變異系數賦權法的成本函數,如式(29)所示:

g=CVTe×μTe+CVψs×μψs

(29)

基于變異系數賦權法的永磁同步電機模型預測轉矩控制仿真波形如圖14～16所示,控制性能如表6所示。

表6 基于變異系數賦權法的系統性能

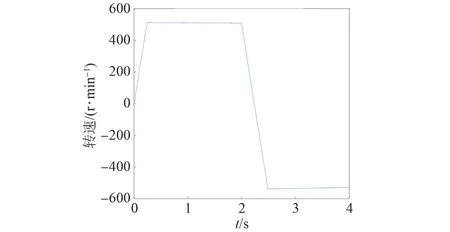
圖14 基于變異系數賦權法的電機轉速

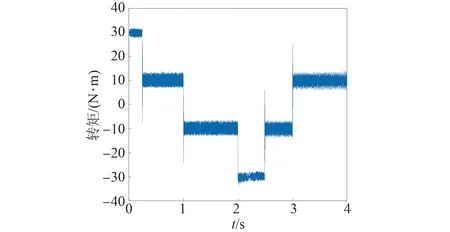
圖15 基于變異系數賦權法的電機轉矩

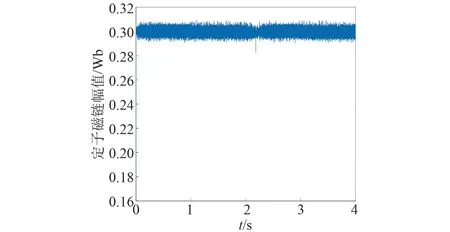
圖16 基于變異系數賦權法的電機定子磁鏈幅值

2.5 基于熵值賦權法

熵值賦權法是通過熵值判斷指標的離散程度與權重的客觀評價法,可用于權重系數設計[27]。

基于熵值賦權法的永磁同步電機模型預測轉矩控制算法步驟如下。

步驟一,計算標幺化后的各成本函數的比值,如式(30)和式(31)所示:

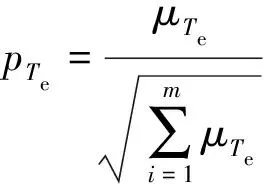
(30)

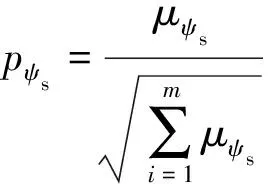
(31)

式中:m為備選電壓矢量數目,這里取m=7。

步驟二,求各指標的信息熵,如式(32)和式(33)所示:

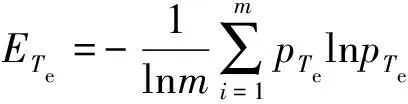
(32)

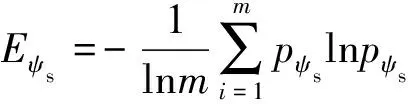
(33)

步驟四,計算信息冗余度,如式(34)和式(35)所示:

DTe=1-ETe

(34)

Dψs=1-Eψs

(35)

步驟五,得到基于熵值賦權法的成本函數,如式(36)所示:

g=DTeμTe+Dψsμψ

(36)

基于熵值賦權法的永磁同步電機模型預測轉矩控制仿真波形如圖17～19所示,控制性能如表7所示。

表7 基于熵值賦權法的系統性能

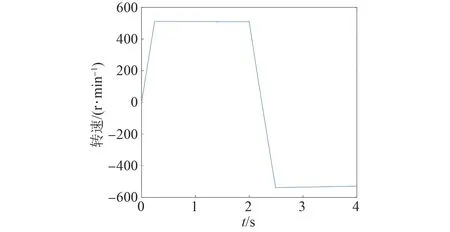
圖17 基于熵值賦權法的電機轉速

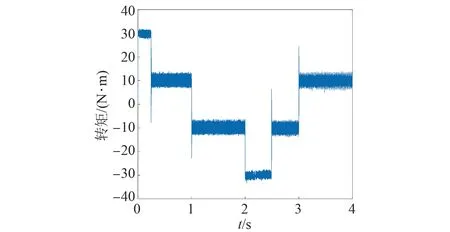
圖18 基于熵值賦權法的電機轉矩

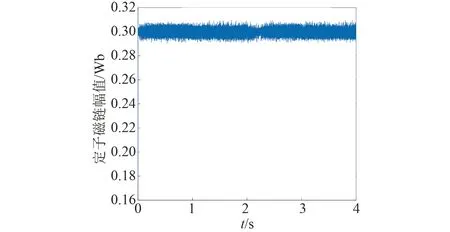
圖19 基于熵值賦權法的電機定子磁鏈幅值

綜上,不同控制策略下,永磁同步電機模型預測轉矩控制系統性能如表8所示。

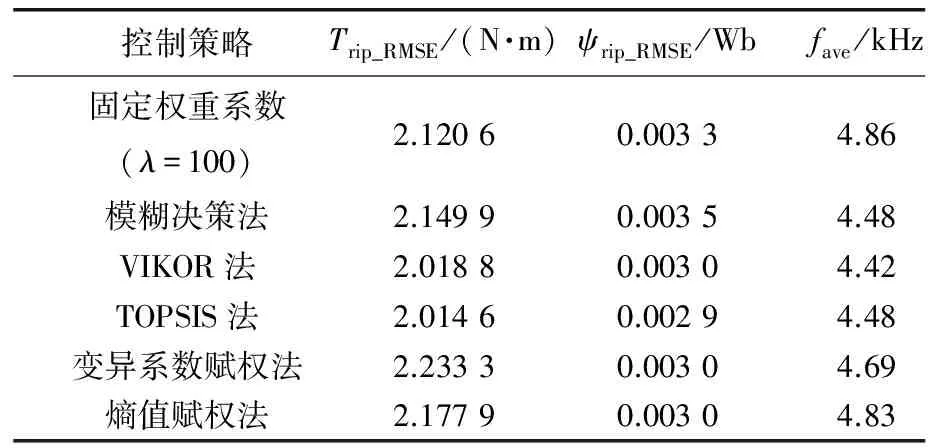
表8 永磁同步電機模型預測轉矩控制系統性能

對比不同策略的控制效果可知,基于客觀評價的永磁同步電機模型預測轉矩控制具有可行性。客觀評價方法均基于標幺化的獨立成本函數,模糊決策、VIKOR和TOPSIS為選擇折衷解,變異系數法和熵權法基于指標離散程度進行客觀賦權。不同策略的控制性能存在一定的差異,但整體基本相當。由綜合性能對比可知,TOPSIS的控制性能相對最優。

3 考慮開關次數控制的客觀評價法

將開關次數控制也作為控制目標之一,開關次數控制成本函數如式(37)所示:

gswitching=2×[|Sa(k+1)-Sa(k)|+

|Sb(k+1)-Sb(k)|+|Sc(k+1)-Sc(k)|]

(37)

式中:Sa(k)、Sb(k)和Sc(k)分別為當前時刻逆變器三相開關狀態;Sa(k+1)、Sb(k+1)和Sc(k+1)分別為下一時刻施加電壓矢量對應的開關狀態。

由于兩電平逆變器存在的開關狀態是確定且有限的,每個控制周期中對應開關狀態的開關切換次數也是確定的,如表10所示。其中零電壓矢量V0所對應的開關狀態有兩種,分別為000和111,當前開關狀態切換到V0的開關次數根據開關次數最小化原則確定。

3.1 基于標幺化法

對表9中的開關次數控制成本函數進行標準化,標準化的開關次數控制成本函數μswitching如表10所示。

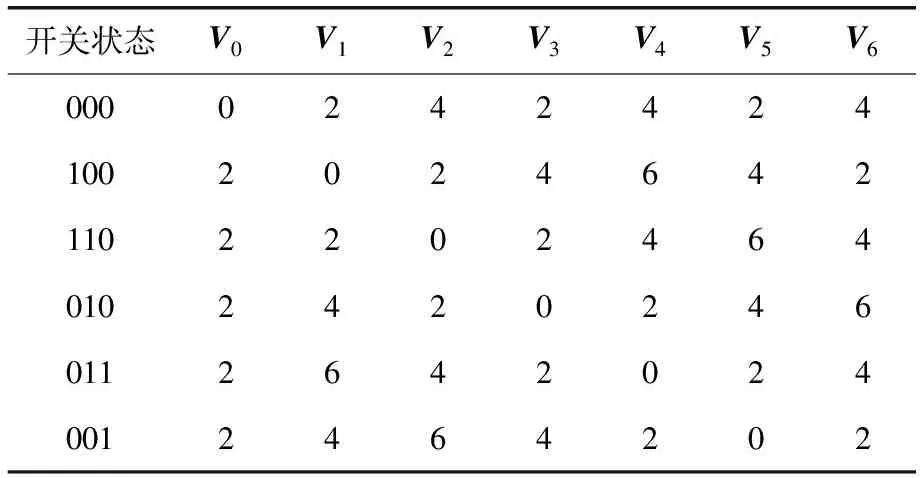
表9 開關次數控制的成本函數gswitching

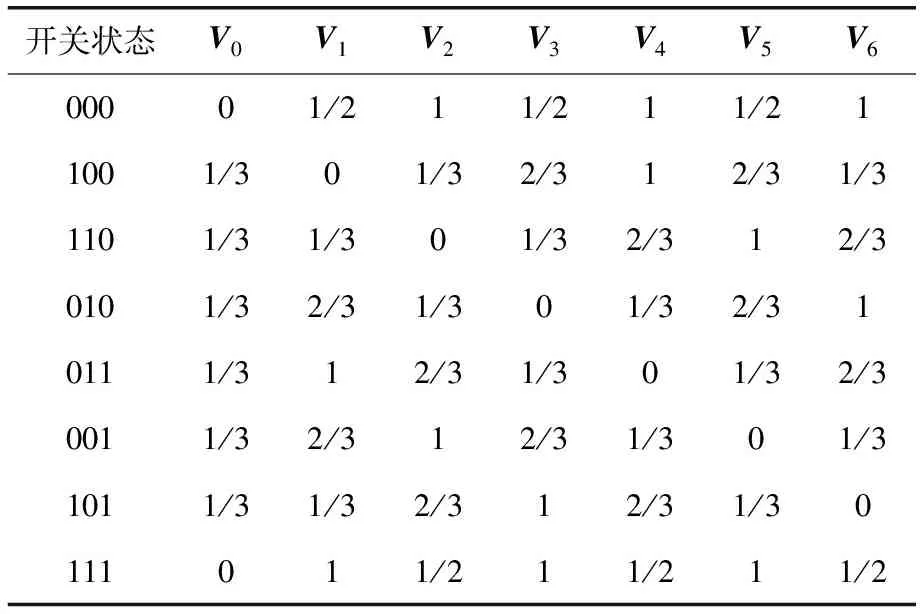
表10 標準化的開關次數控制成本函數μswitching

基于標幺化法的模型預測轉矩控制成本函數如式(38)所示:

g=μTe+μψs+μswitching

(38)

式中:μswitching為標幺化的開關次數控制成本函數。

基于標幺化法的永磁同步電機模型預測轉矩控制仿真波形如圖20～22所示。此時,系統控制性能較差[28]。

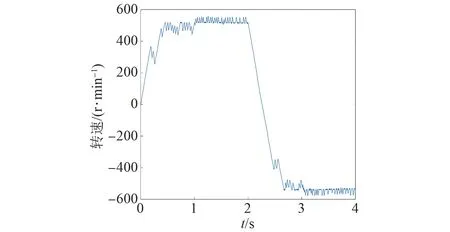
圖20 基于標幺化法的電機轉速

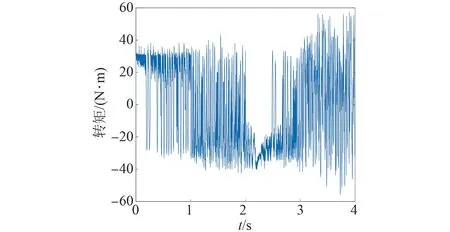
圖21 基于標幺化法的電機轉矩

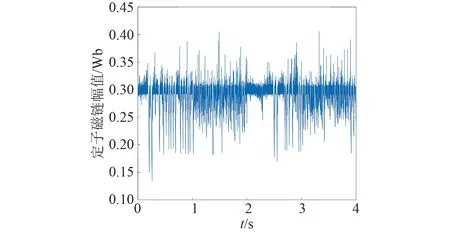
圖22 基于標幺化法的電機定子磁鏈幅值

3.2 基于模糊決策法

采用最大隸屬度算子對標幺化的成本函數進行模糊化,如式(39)所示。與上文相同,模糊決策法下一時刻輸出令μD最小值的電壓矢量即:

μD=max(μTe,μψs,μswitching)

(39)

基于模糊決策法的永磁同步電機模型預測轉矩控制仿真波形如圖23～25所示。此時,系統控制性能較差。

圖23 基于模糊決策法的電機轉速

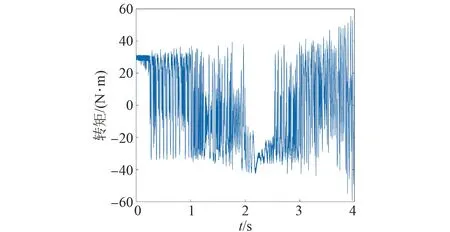
圖24 基于模糊決策法的電機轉矩

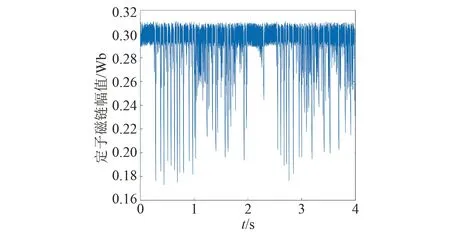
圖25 基于模糊決策法的電機定子磁鏈

3.3 基于VIKOR法

增加開關次數控制的VIKOR法群體效用值S與個體遺憾值R如式(40)和式(41)所示。與上文相同,VIKOR法輸出令折衷決策指標值最小的電壓矢量。

S=μTe+μψs+μswitching

(40)

R=max(μTe,μψs,μswitching)

(41)

基于VIKOR法的永磁同步電機模型預測轉矩控制仿真波形如圖26～28所示。此時,系統控制性能較差。

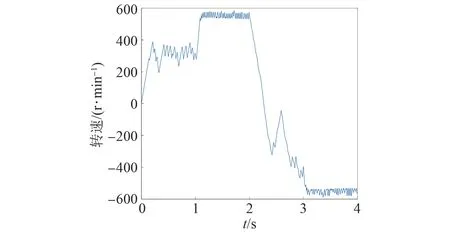
圖26 基于VIKOR法的電機轉速

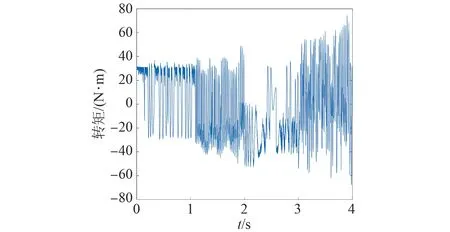
圖27 基于VIKOR法的電機轉矩

3.4 基于TOPSIS法

增加開關次數控制的TOPSIS法備選狀態與最優解和最劣解之間的差距,如式(42)和式(43)所示。與上文相同,TOPSIS法輸出令接近系數最大的電壓矢量。

D+=

(42)

D-=

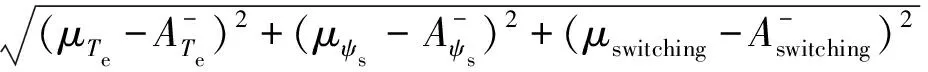
(43)

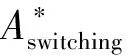
基于TOPSIS法的永磁同步電機模型預測轉矩控制仿真波形如圖29～31所示。此時,系統控制性能較差。

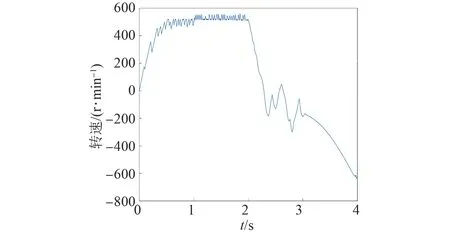
圖29 基于TOPSIS法的電機轉速

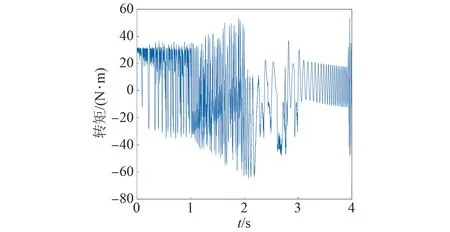
圖30 基于TOPSIS法的電機轉矩

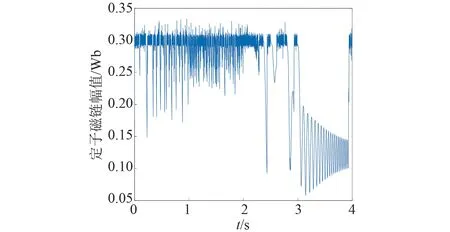
圖31 基于TOPSIS法的電機定子磁鏈幅值

3.5 基于變異系數賦權法

標幺化的開關次數控制成本函數的平均值、標準差和變異系數如表11所示。

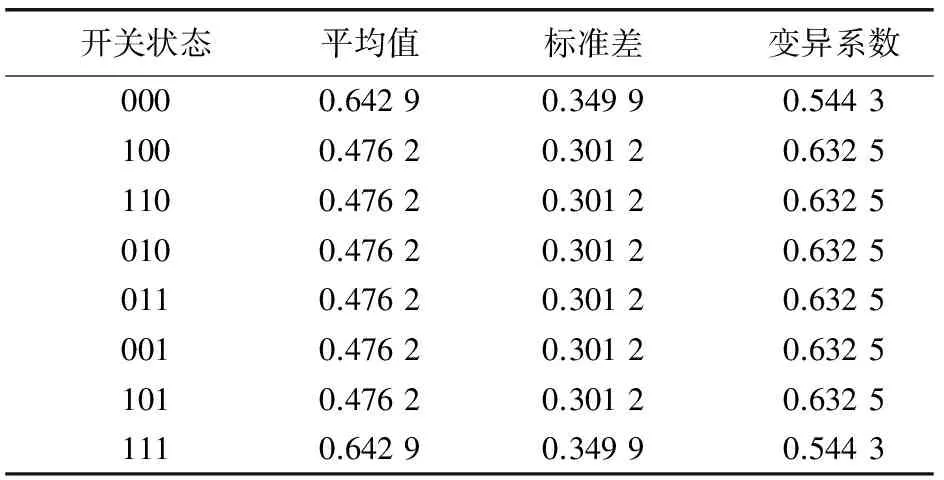
表11 開關次數控制成本函數平均值、標準差和變異系數

基于變異系數權重系數設計的成本函數如式(44)所示:

g=CVTe×μTe+CVψs×μψs+CVswitching×μswitching

(44)

式中:CVswitchig為開關次數控制成本函數的變異系數。

基于變異系數賦權法的永磁同步電機模型預測轉矩控制仿真波形如圖32～34所示。此時,系統控制性能較差。

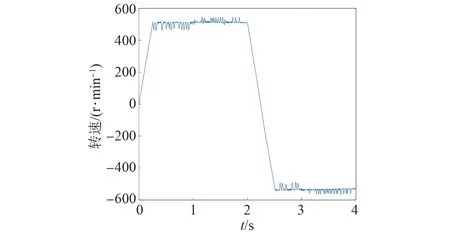
圖32 基于變異系數賦權法的電機轉速

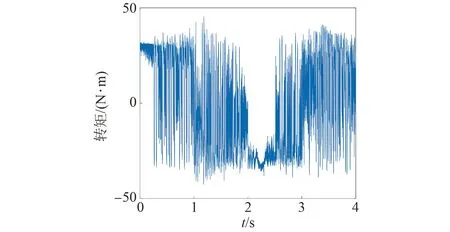
圖33 基于變異系數賦權法的電機轉矩

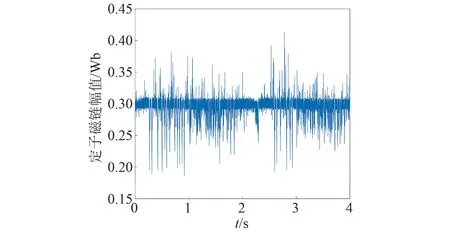
圖34 基于變異系數賦權法的電機定子磁鏈幅值

3.6 基于熵值賦權法

基于熵值賦權法的成本函數如式(45)所示:

g=DTeμTe+Dψsμψs+Dswitchingμswitching

(45)

式中:Dswitching為開關次數控制成本函數的信息冗余度。

基于熵值賦權法的永磁同步電機模型預測轉矩控制仿真波形如圖35～37所示。此時,系統控制性能較差。

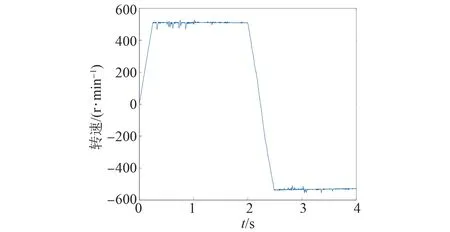
圖35 基于熵值賦權法的電機轉速

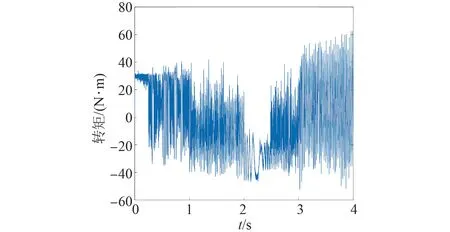
圖36 基于熵值賦權法的電機轉矩

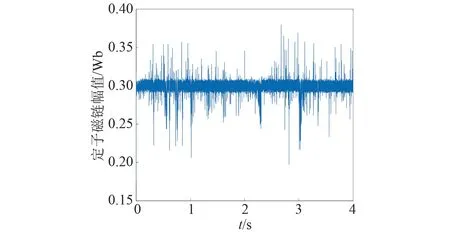
圖37 基于熵值賦權法的電機定子磁鏈幅值

由仿真結果可知,當控制目標為磁鏈、轉矩和開關次數時,模糊決策法、VIKOR法、TOPSIS法的電機系統控制性能較差[29-30]。變異系數賦權法和熵值賦權法基于離散程度對成本函數進行賦權,但指標離散程度與控制目標的重要性并不等價,無法改善系統控制性能。

4 結 語

對于僅考慮磁鏈和轉矩控制的永磁同步電機模型預測轉矩控制,模糊決策法、VIKOR法、TOPSIS法、變異系數賦權法和熵值賦權法等客觀評價法是可行的,無需權重系數,但在一定程度上增加計算負擔。不同策略的控制性能存在一定的差異,但整體基本相當。由綜合性能對比可知,TOPSIS法的控制性能相對最優。當控制目標增加開關次數控制,控制目標重要性并不相同,客觀評價方法效果并不明顯。