基于改進PLL的永磁同步電機ASMO無傳感器控制
孫旭霞, 吳 迪, 王若琪, 賀思俊, 韋明旸, 崔偉杰
(1.西安理工大學 自動化與信息工程學院,陜西 西安 710048;2.陜西省復雜系統控制與智能信息處理重點實驗室,陜西 西安 710048)
0 引 言
永磁同步電機(PMSM)有著結構簡單、效率高等優點,被廣泛應用在機床、新能源汽車等行業[1-2]。在高性能的PMSM控制系統中為準確獲取轉子位置,需在轉子上安裝機械傳感器。但傳感器精度受環境影響較大且會增加系統成本[3-4]。因此PMSM無位置傳感器控制技術成為國內外學者的研究熱點。
目前無傳感器控制算法有模型參考自適應算法,擴展卡爾曼濾波器算法,以及滑模觀測器算法(SMO)等[5]。穩定的滑模控制算法具有很強的魯棒性,使系統性能不受參數攝動及外部擾動影響[6-7]。因此在電機高速控制中,滑模觀測器算法得到研究者們的青睞,但SMO存在抖振,會降低位置觀測精度[8]。文獻[9]用sigmoid函數替換開關函數,并在sigmoid函數中引入狀態變量,根據狀態變量大小設計邊界層厚度可變的sigmoid函數來抑制滑模抖振,但會降低系統響應速度。文獻[10]利用二階廣義積分器(SOGI)的無靜差跟蹤特性代替低通濾波器,避免相位延遲;并在鎖相環中加入陷波器來濾除反電動勢低次諧波,但其反電動勢諧波模型和滑模觀測器模型不在同一坐標系下。
為解決上述問題,本文研究基于自適應滑模觀測器(ASMO)的表貼式永磁同步電機(SPMSM)無傳感器控制方法,主要由非奇異快速終端滑模面(NFTSMS)以及由SMO增益根據反電動勢大小自調整和新的滑模函數形成的新趨近律組成。并設計了改進鎖相環(PLL),在電機正反轉時能準確獲取轉子位置信息并解決反電動勢低次諧波干擾對位置估計精度影響的問題。
1 傳統滑模觀測器
1.1 SPMSM數學模型
假定SPMSM為理想的電機,而且滿足條件:(1)忽略電機鐵心的飽和;(2)不計電機中的渦流和磁滯損耗;(3)電機中三相電流為正弦波電流,則SPMSM在αβ兩相靜止坐標系中的電壓方程如式(1)所示:
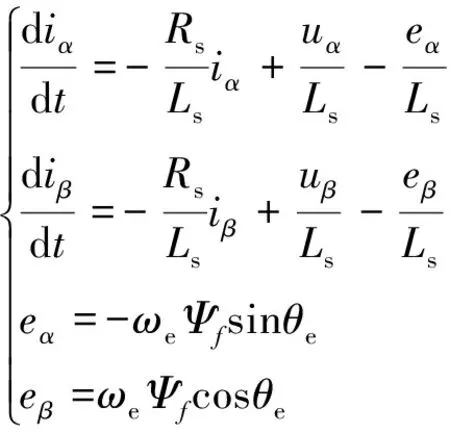
(1)
式中:iα、iβ分別為靜止坐標系下的定子電流;uα、uβ分別為靜止坐標系下的定子電壓;eα、eβ分別為反電動勢在αβ坐標軸上的分量;Rs、Ls分別為定子電阻和定子電感;ωe為電角速度;Ψf為永磁體磁鏈;θe為電角度。
由式(1)可知,反電勢中含有轉子位置信息和轉速信息,因此可使用SMO法獲得轉子位置和轉速信息。
1.2 傳統滑模觀測器
在傳統SMO中,采用開關函數對PMSM數學模型進行重構如式(2)所示:
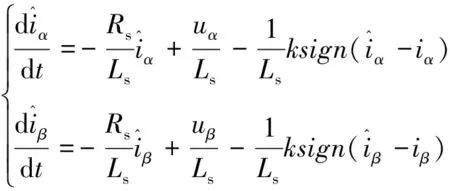
(2)
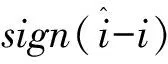
其中滑模面s可表示為
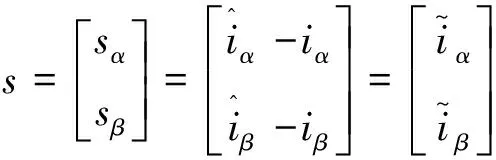
(3)
式(2)減去式(1)得電流誤差方程:
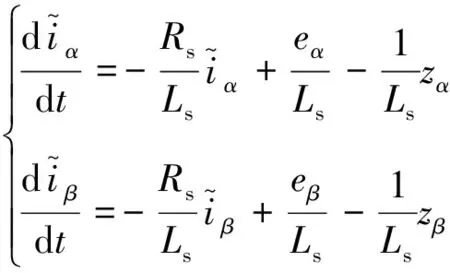
(4)
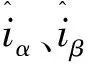
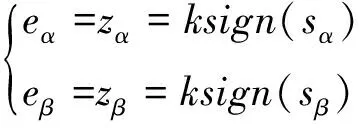
(5)
為了保證滑動運動的穩定性,SMO增益應足夠大,以滿足以下到達條件:
k>max (|eα|,|eβ|)
(6)
由式(2)可知,所設計的滑模觀測器能夠觀測PMSM反電動勢,得到轉子位置信息,傳統滑模觀測器控制框圖如圖1所示。
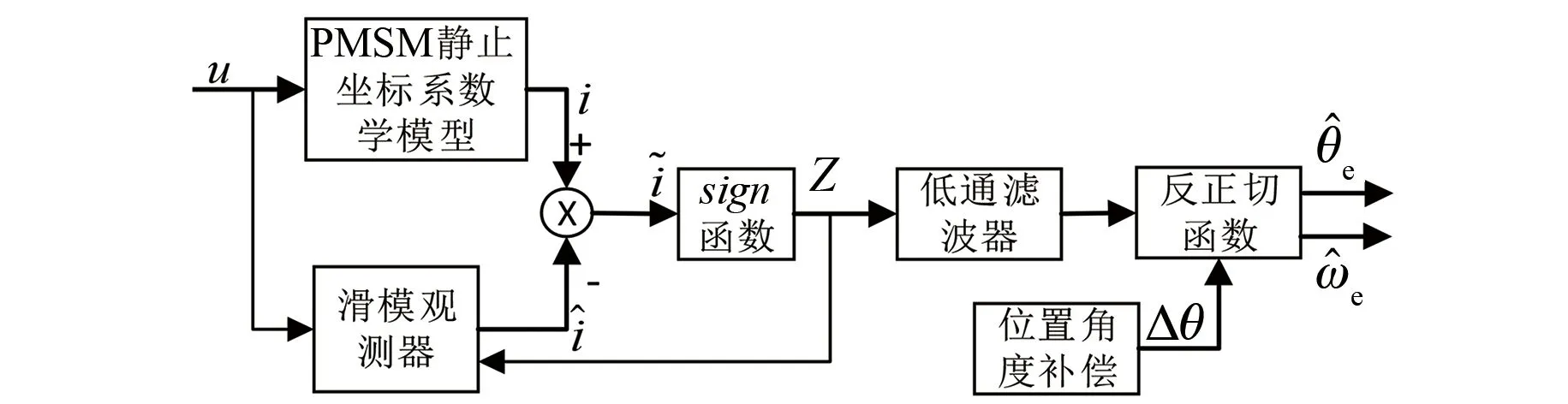
圖1 傳統滑模觀測器控制框圖
由圖1可知,觀測反電動勢經低通濾波器濾除由開關頻率產生的高次諧波,經反正切計算獲取轉子位置。但使用低通濾波器會導致相位延遲,而且位置補償角計算復雜。穩定的滑模控制算法要求滑模增益足夠大,但增益過大會導致控制系統產生抖振,故采用滑模增益自調整,可有效降低滑模抖振[11]。
2 自適應滑模觀測器
本文所設計的自適應滑模觀測器如圖2所示。
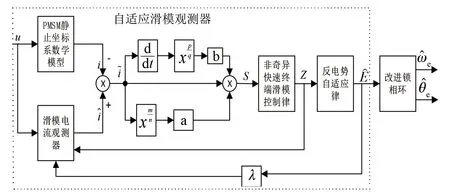
圖2 自適應滑模觀測器結構圖
2.1 非奇異快速終端滑模面
本文所使用的非奇異快速終端滑模面為[12]
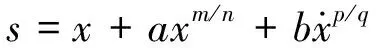
(7)
式中:a,b>0;m/n>1;p和q為正奇數且2>p/q>1,m/n>p/q;x為系統狀態誤差。
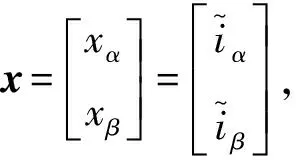
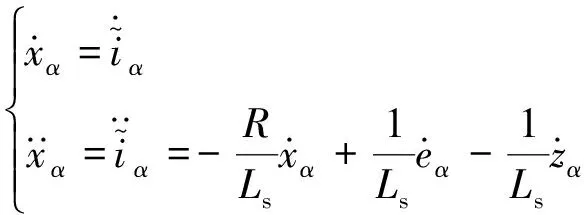
(8)
分析α軸,對式(7)進行求導并將式(8)代入得:
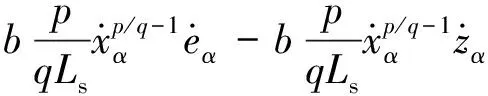
(9)
2.2 改進指數趨近律
本文所設計的改進指數趨近律為
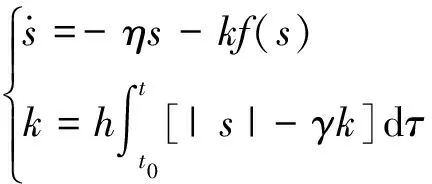
(10)
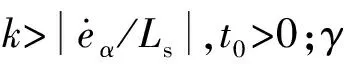
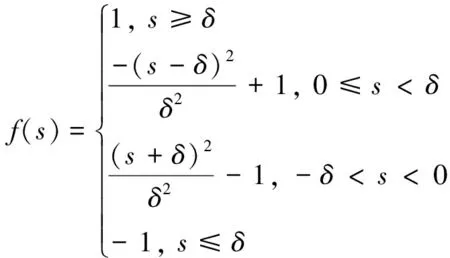
(11)
聯立式(9)和式(10),可得到帶有積分的控制律,即反電動勢觀測值zα:
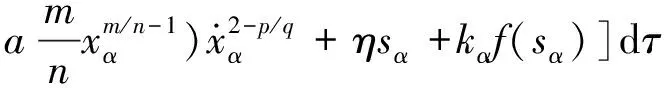
(12)
2.3 穩定性證明
選取Lyapunov函數為
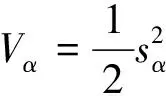
(13)
對式(13)求一階導數得:
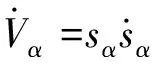
(14)
式(12)反電動勢觀測值zα代入式(9)得:
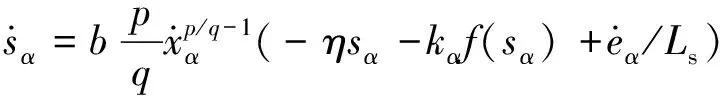
(15)
將式(15)代入式(14)得:
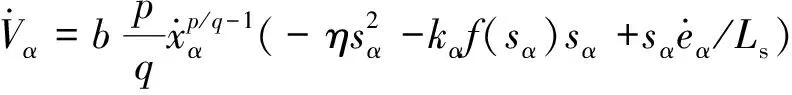
(16)
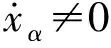
同理可得β軸反電動勢觀測值zβ,且系統漸近穩定。
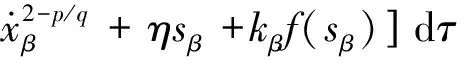
(17)
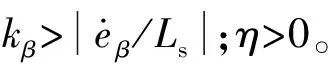
3 反電動勢自適應律
為加快系統響應速度,設計反電動勢自適應律為
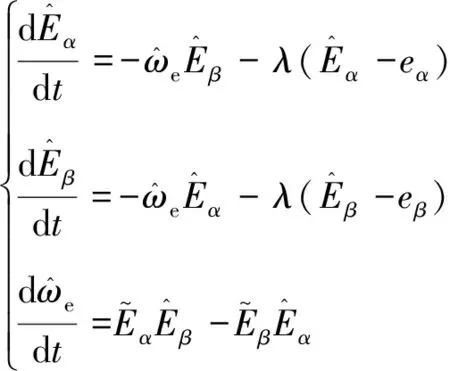
(18)
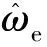
永磁同步電機反電動勢模型可以表示為:
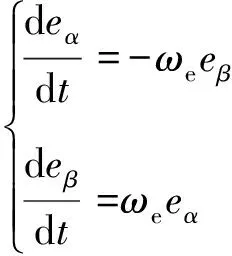
(19)
用式(18)減去式(19)得到反電動勢誤差方程,表達式為
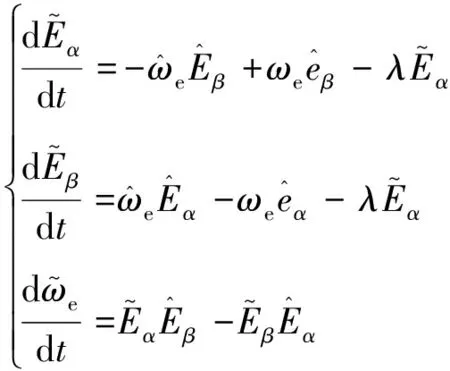
(20)
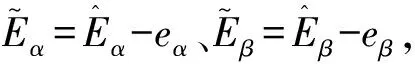
進行穩定性證明,選取李雅普諾夫函數為

(21)
對式(21)求導,并代入式(20)得:

(22)
式(22)滿足李雅普諾夫穩定性條件,故所設計的反電勢自適應律漸近穩定,可從更新后的反電動勢估計值中獲取電機轉子位置信息[13]。
4 改進鎖相環
使用反正切法計算轉子位置,位置補償角計算復雜且除法的存在會放大反電動勢高頻抖振,故采用鎖相環獲取轉子位置。
4.1 傳統鎖相環
傳統鎖相環的結構圖如圖3所示。
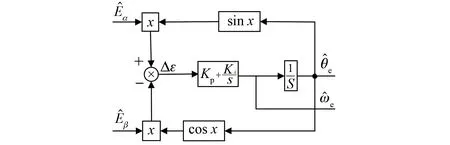
圖3 傳統鎖相環結構圖
圖中Kp和Ki分別為PI調節器的比例系數和積分系數。由圖3可以得到傳統鎖相環的誤差信號為
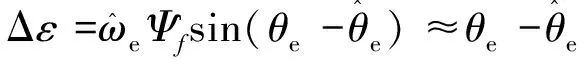
(23)
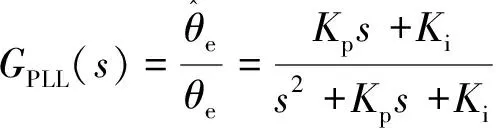
(24)
則其誤差傳遞函數EPLL(s)為
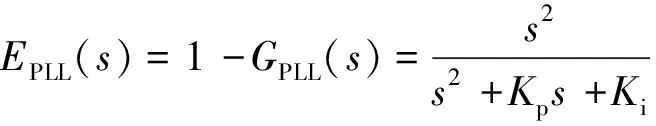
(25)
當輸入的θe(s)含有速度斜波ΔR,位置階躍Δθ和速度階躍Δω時,其表達式為
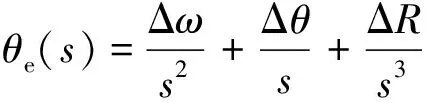
(26)
此時,其穩態誤差分別為
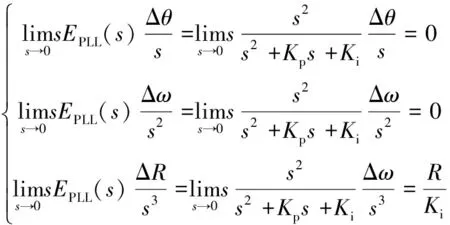
(27)
由式(27)得傳統鎖相環對Δθ,Δω的穩態誤差為0;但對ΔR具有穩態誤差,使得電機正反轉切換失敗[11]。
4.2 改進鎖相環鑒相器和環路濾波器
改進鎖相環結構圖如圖4所示。
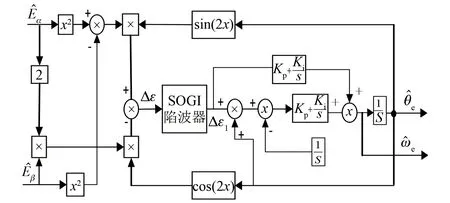
圖4 改進鎖相環結構圖
由圖4可得:
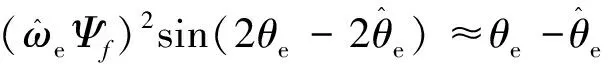
(28)
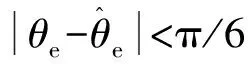
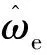
由于逆變器死區,開關管壓降和電機磁通諧波變化,導致電流中含有大量5次和7次諧波[14-15]。由于電機結構對稱型,反電勢中含有5次和7次諧波,影響位置觀測精度。
鑒于此,本文利用SOGI的無靜差跟蹤特性及陷波功能濾除5次和7次諧波。SOGI的結構圖如圖5所示。
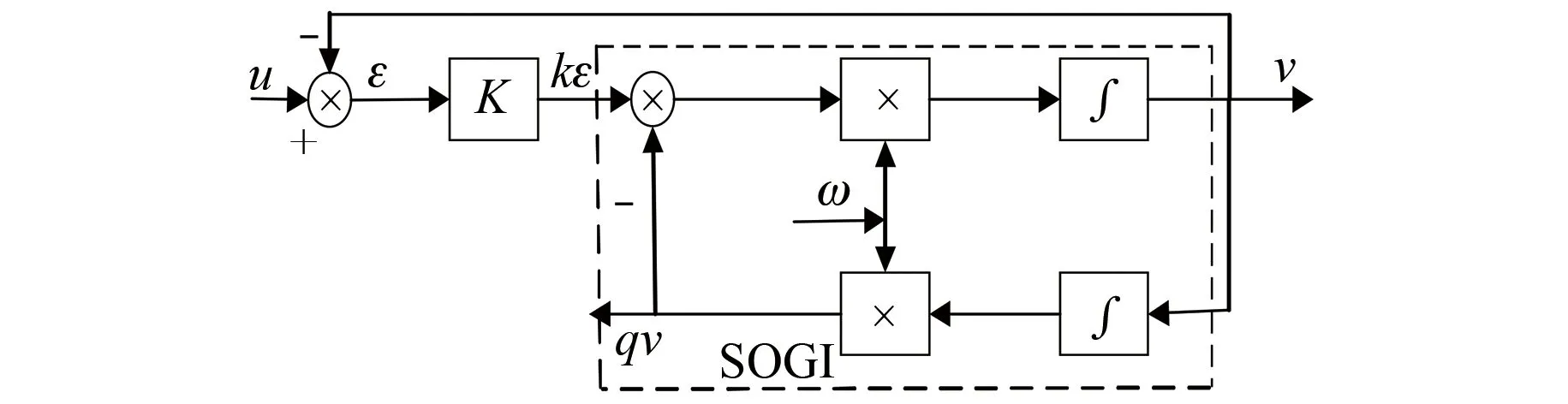
圖5 二階廣義積分器SOGI結構圖
由圖5可得如下傳遞函數:
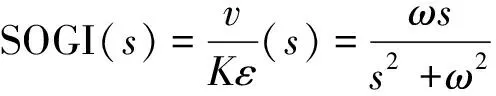
(29)
(30)
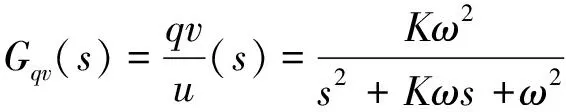
(31)
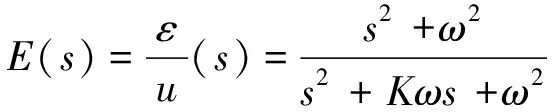
(32)
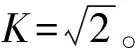
將逆變器三相電壓諧波經Clark變換后,得到5次和7次反電勢諧波eαh和eβh,其在αβ軸下的表達式如式(33)所示:
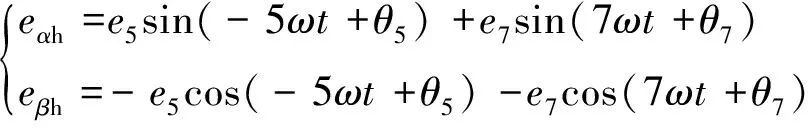
(33)
式中:e5和e7分別為5次和7次諧波反電動勢幅值;θ5和θ7分別為5次和7次諧波反電動勢初始相位。
2E5E7sin(θ5+θ7)
(34)
由式(34)得,此時eαh,eβh中的5次和7次諧波都轉化為Δε中的12次諧波,可利用SOGI陷波器無靜差跟蹤特性抑制12次諧波,且不影響鎖相環位置估計。經陷波器處理后,系統等效閉環傳遞函數GzPLL(s)為
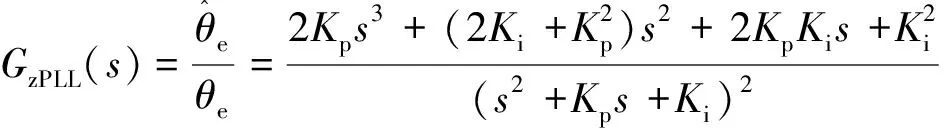
(35)
則其誤差傳遞函數EzPLL(s)為
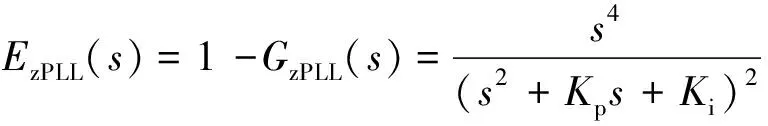
(36)
在輸入信號θe(s)下,此時系統穩態誤差為
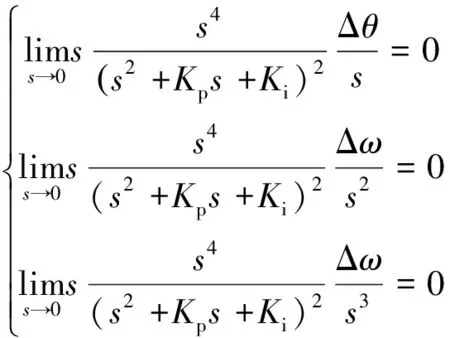
(37)
由式(37)得改進鎖相環對Δθ,Δω和ΔR的穩態誤差皆為0。改進后可準確獲取電機正反轉時的位置信息,使電機直接進行正反轉。
5 仿真結果
為驗證所研究控制算法可行性,本文采用id=0的矢量控制方案,在MATLAB/Simulink上搭建仿真模型,如圖6所示。仿真所用的SPMSM具體參數見表1,ASMO和改進PLL具體參數見表2。轉速環PI參數:Kp=0.95,Ki=28.5;電流環PI參數:Kp=Ls×2 000,Ki=Rs×2 000。方法一,傳統SMO結合傳統PLL;方法二,基于NFTSMS的SMO結合PLL;以及本文提出的方法三,ASMO結合改進PLL三種控制策略進行仿真試驗。
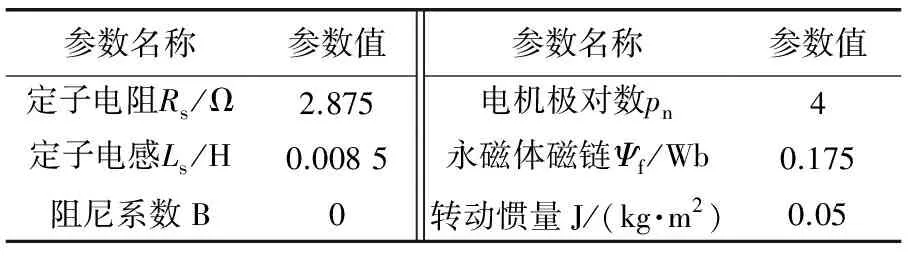
表1 SPMSM主要參數
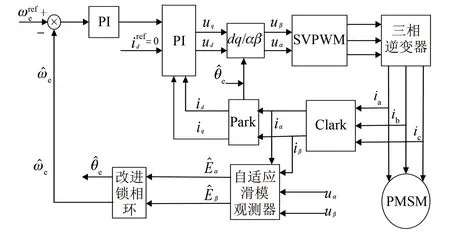
圖6 基于改進鎖相環的PMSM自適應滑模觀測器無位置傳感器控制框圖
5.1 轉速跟蹤
工況一:空載且給定轉速1 000 r/min,圖7為此工況下三種控制策略下的仿真結果,可知三種控制策略下估計轉速均能跟蹤電機實際轉速,穩態時轉速穩態誤差范圍分別為[-40,40]、[-0.06,0.06]、[-0.018,0.018]。分析可得本文所提的ASMO結合改進PLL控制策略轉速穩態誤差最小。
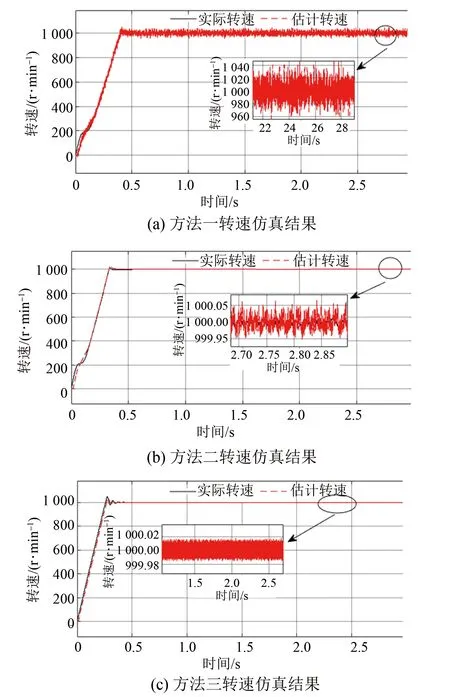
圖7 空載且轉速為1 000 r/min時轉速仿真結果
工況二:在0.9秒電機轉速由800 r/min突變至1 200 r/min且在1.6秒負載由1突變至3。圖8為此工況三種控制策略下的仿真結果,可得在三種控制策略下,當轉速為800 r/min時,轉速穩態誤差范圍分別為[-40,40]、[-0.08,0.08]、[-0.016,0.02];負載突變時0.1秒回到穩態,帶載能力良好;當轉速為1 200 r/min時,轉速穩態誤差范圍分別為[-40,40]、[-0.07,0.07]、[0.02,0.02]。分析可得本文所提ASMO結合改進PLL控制策略轉速穩態誤差最小。
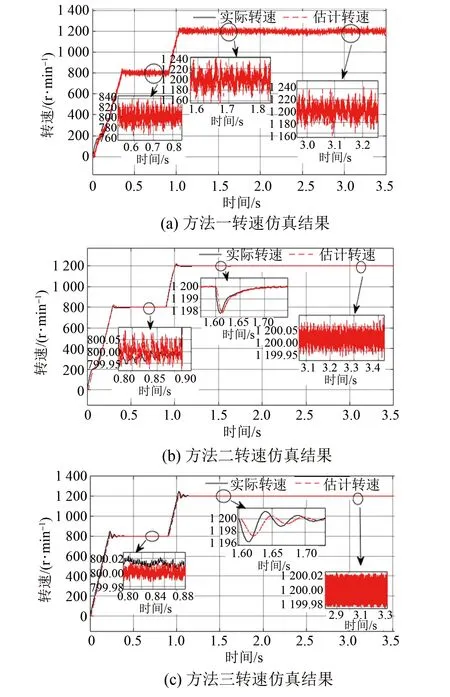
圖8 0.9 s電機轉速由800 r/min突變至1 200 r/min且1.6 s負載由1突變至3時轉速仿真結果
工況三:在0.9秒電機轉速由800 r/min突變至-1 000 r/min且在1.8 s負載由0突變至2。圖9為此工況方法三控制策略下的仿真結果,可知本文所提ASMO結合改進鎖相環控制策略在轉速為800 r/min時,轉速穩態誤差范圍為[-0.016,0.002],負載突變時0.1秒回到穩態,在-1 000 r/min時轉速穩態誤差范圍為[-0.018,0.016]。在電機反轉時本文所提ASMO結合改進鎖相環控制策略依舊有良好的轉速跟蹤性能。
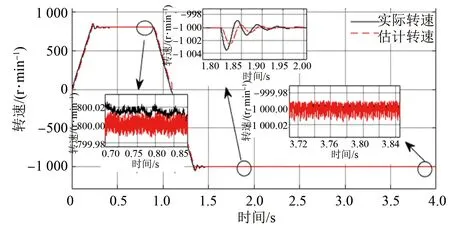
圖9 0.9 s電機轉速由800 r/min突變至-1 000 r/min且1.8 s負載由0至2時方法三轉速仿真結果
5.2 轉子位置跟蹤
在工況一下,由圖10得轉子初始位置跟蹤時間和跟蹤延遲時間在三種控制策略下分別為0.12 s,0.014 5 s;0.108 s,0.013 5 s;0.087 85 s,0.000 45 s。分析可得本文所提ASMO結合改進鎖相環控制策略位置跟蹤及延遲時間最小,初始位置跟蹤波動小。
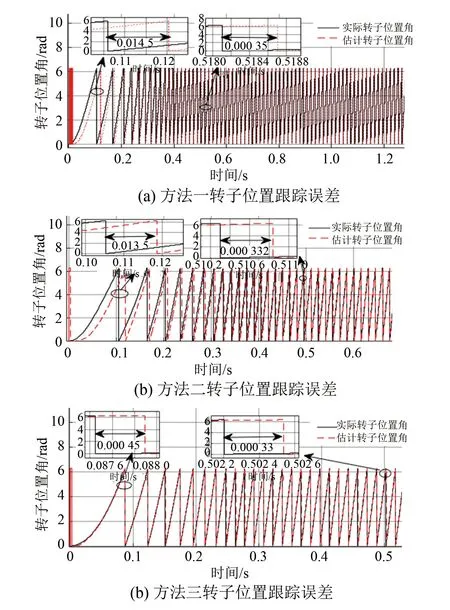
圖10 空載且給定轉速1 000 r/min時轉子位置
5.3 反電動勢諧波及兩相旋轉電流
在工況一下,前20個周期內由圖11得反電動勢諧波在三種控制策略下分別為466.35%,388.18%,170.09%。由圖12得穩態時方法一電流波動最大,方法二和三電流波動范圍相差不大,方法三起動電流小。分析可得本文所提ASMO結合改進鎖相環控制策略的反電動勢諧波最小,驗證所設計改進鎖相環的有效性。
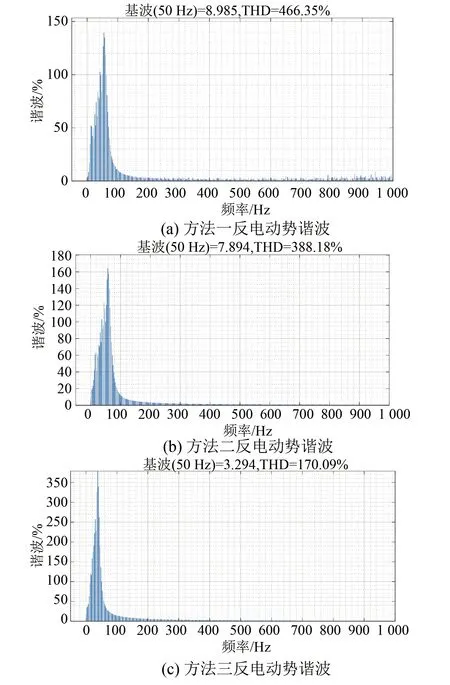
圖11 空載且給定轉速1 000 r/min時反電動勢諧波
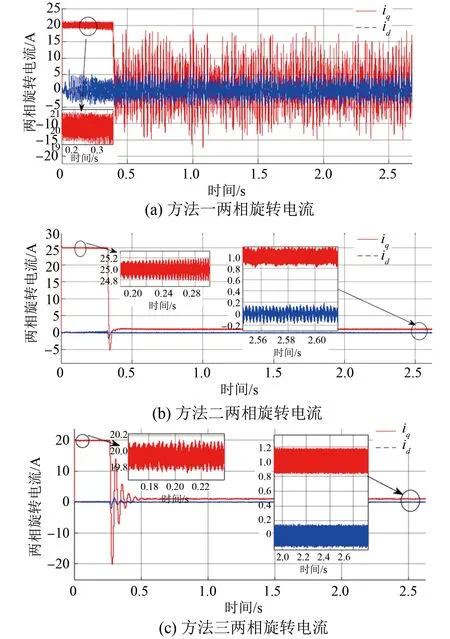
圖12 空載且給定轉速1 000 r/min時兩相旋轉電流
6 結 語
針對滑模抖振問題,設計了一種新的基于ASMO的SPMSM無傳感器控制方法。使用李雅普諾夫法證明算法穩定性,通過MATLAB進行仿真驗證,得出以下結論。
(1) 采用NFTSMS,引入SMO增益值根據反電動勢自調整,推導得出新的控制律,能顯著降低滑模抖振。相比傳統SMO既避免相位延遲,又減小了位置跟蹤延遲時間。
(2) 設計改進PLL,同時引入二階廣義積分器對反電動勢低次諧波進行抑制,不僅能在電機正反轉時準確獲取轉子位置,還能提高轉子位置估計精度,使轉速穩態誤差降至0.02 r/min。

