永磁同步直線電機單齒切向電磁力分析

劉津成, 夏加寬, 馬功臣

(沈陽工業大學 電氣工程學院,遼寧 沈陽 110870)

0 引 言

近年來,隨著電機行業的不斷發展,永磁同步直線電機(PMSLM)得到了更加廣泛的應用,比如PMSLM驅動的物料輸送機、起重設備、空氣壓縮機以及各種電動門等[1]。由于PMSLM具有特殊的直線結構,不存在繞組端部,憑借更高的功率因數、效率、推力密度及定位精度,在高度集成化、輕量化的應用場合受到越來越多的關注[2-4]。

在旋轉電機中,引起分數槽繞組永磁電機振動的激振源分別為徑向電磁力和切向電磁力[5],切向電磁力分為全局切向電磁力和局部切向電磁力即單齒切向電磁力。現有研究中,大多數學者關注的都是徑向電磁力和全局切向電磁力又稱磁阻力[6]。國內外許多學者對磁阻力進行了分析計算。文獻[7]通過解析法,精確計算并歸納邊端力與齒槽電磁力的一般規律,合理設置了補償器參數。文獻[8]研究了端部齒相對次級永磁體不同位置時對磁阻力的影響,通過優化端部齒來削弱端部力。文獻[9]提出初級鐵心齒開虛擬槽結構,對比分析四種不同虛擬槽型,最后得出矩形槽對齒槽力的抑制效果最顯著。文獻[10]指出直線電機的邊端力并非理想的正弦波,存在奇、偶次諧波,提出利用有限元來分析邊端力,對其幅值和相位進行快速傅里葉變換,確定最佳初級長度,并反復迭代以提高最佳初級鐵心長度的精度。由于直線電機存在邊緣效應,初級端部和中部的齒的受力情況也不盡相同[11]。

分數槽電機單齒切向電磁力通過電機初級齒部的杠桿效應引起軛部振動,振動方向為法向,在低頻段單齒切向電磁力引起的振動和徑向電磁力引起的振動對電機性能的影響幾乎具有同等貢獻[12]。因此,對電機單齒切向電磁力進行分析研究很有必要。

本文以PMSLM為研究對象,利用麥克斯韋方程組建立了單齒切向電磁力模型,并對電機氣隙磁密進行仿真計算,分析了單齒切向電磁力產生振動的原因,利用ANSYS Workbench平臺對電機的模態和振動加速度進行計算,為PMSLM的設計和振動優化提供了參考。

1 PMSLM模型的設計與分析

研究表明,當直線電機的極數和槽數互為質數時,可以有效減小電機推力波動從而提高電機效率[13],因此本文的PMSLM采用11極12槽的極槽配合。

在旋轉電機中,首先需要根據主要尺寸關系式來確定電機中有效電磁部分的主要尺寸,PMSLM同樣也需要根據關系式來確定主要尺寸[14]。電磁推力與主要尺寸計算關系式如式(1)所示:

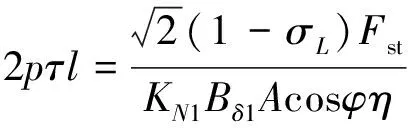
(1)

式中:p為極對數;τ為電機極距;l為永磁體縱向長度;(1-σL)為壓降系數;Fst為電機電磁推力;KN1為繞組系數;η為電機效率;A為電機線負荷;Bδ1為氣隙磁密基波幅值;cosφ為功率因數。

PMSLM的初級繞組分為隔齒繞組和全齒繞組,本文所設計的電機采用的是全齒繞組形式,可以有效提高鐵心材料利用率,提高電機性能[15]。同時考慮到電機實際制造過程中的繞線問題,還需在初級兩端加輔助齒,使電機的設計與分析更加合理[16]。

電機的氣隙磁密基波幅值與電磁推力的大小都會隨著永磁體磁化方向長度的增加而增大[17]。因此電機永磁體尺寸可根據式(2)確定:

(2)

式中:Ks為外磁路飽和系數;Kδ為氣隙系數;bm0為預估永磁體的空載工作點;δ為氣隙長度;σ0為空載漏磁系數;μr為相對磁導率。

本文建立的PMSLM模型如圖1所示,其主要結構參數如表1所示。

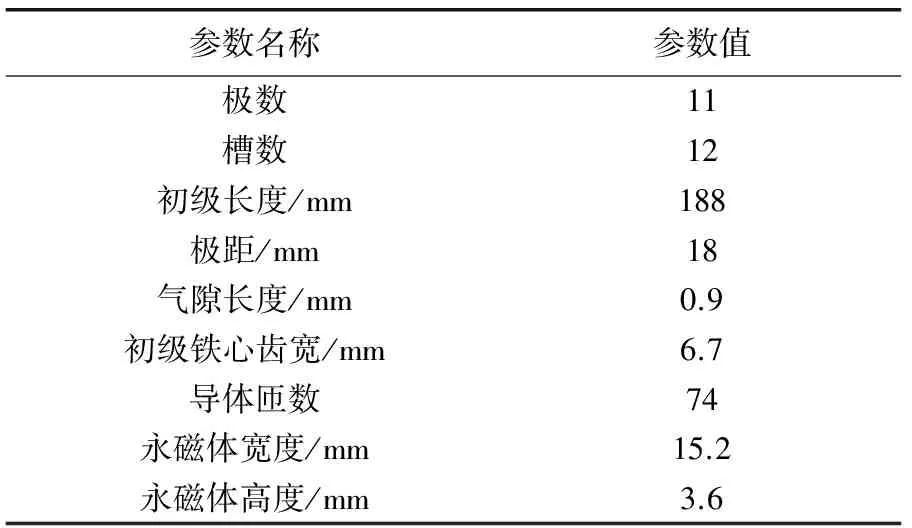
表1 PMSLM主要結構參數

圖1 PMSLM模型

PMSLM模型的磁密云圖和空載反電勢波形如圖2和圖3所示。由圖可知,電機初級齒部磁密最大處為1.5 T,空載反電勢三相對稱,電機設計基本合理。

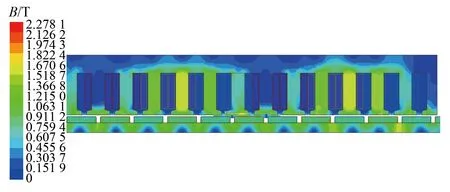
圖2 PMSLM磁密云圖

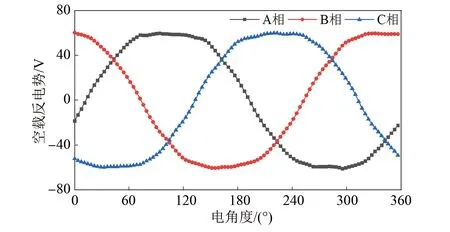
圖3 PMSLM空載反電勢波形

2 PMSLM單齒切向電磁力模型

為了便于分析,本文所采用的PMSLM忽略邊緣效應,只考慮初級中部齒的受力情況。在旋轉電機中,作用在定子齒上的電磁力分為徑向電磁力和切向電磁力[18],而在PMSLM中,初級和次級的耦合磁場在初級齒上產生的電磁力波分為法向電磁力波和切向電磁力波,其解析表達式與旋轉電機類似。根據麥克斯韋應力方程可知,其法向電磁力密度和切向電磁力密度的解析表達式如式(3)所示:

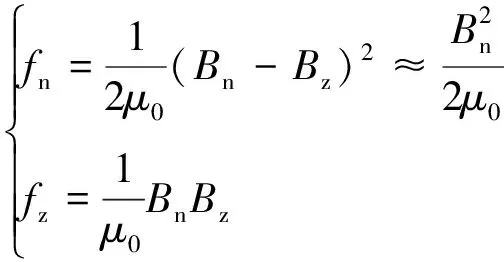
(3)

式中:fn、fz分別為法向和切向電磁力密度;Bn、Bz分別為法向和切向磁密;μ0為真空磁導率。

圖4 選取的初級齒A示意圖

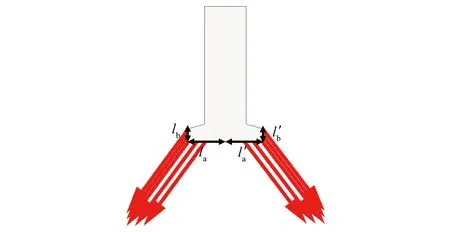
圖5 初級齒A所受電磁力密度示意圖

由于初級齒部的杠桿效應,PMSLM的單齒切向力會引起軛部產生法向振動,即單齒切向力波作用在齒靴頂部的邊緣位置時,初級齒部會產生局部齒槽電磁力波動,引起軛部產生法向振動。所以局部齒槽電磁力波動是單齒切向力產生振動的主要原因。局部齒槽電磁力由作用于初級齒靴兩側的切向力合力引起,左、右兩側齒靴所受到的切向集中力解析表達式如式(4)所示:

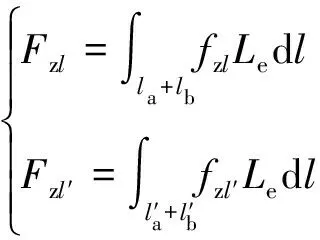
(4)

式中:Le為電機電樞長度。

由于左、右兩端齒靴頂部所受切向集中力的方向相反,因此單齒切向電磁力大小可以由二者的差值確定,如式(5)所示:

ΔFz=Fzl-Fzl′

(5)

3 PMSLM單齒切向電磁力產生振動的原因

利用有限元仿真軟件,計算PMSLM一對極下的氣隙磁密,并對該結果進行快速傅里葉變換(FFT),計算結果如圖6所示。由圖可知,氣隙磁密主要分為三個部分:I、II和III區域。其中,I區域是永磁體所對應的氣隙磁密,波形接近平頂波;II區域是由于電機初級開槽而導致的氣隙磁密,氣隙磁密呈現先減小后增大的變化趨勢,變化范圍是0.65 T至0.9 T;III區域是永磁體之間的極間區域對應的氣隙磁密,其值經過零點呈正負波動。在這三個區域,區域III的波動幅度最大,即極間區域所對應的氣隙磁場畸變最明顯。由FFT結果可知,基波磁密為最大值,奇數次諧波整體要大于相鄰的偶數次諧波。

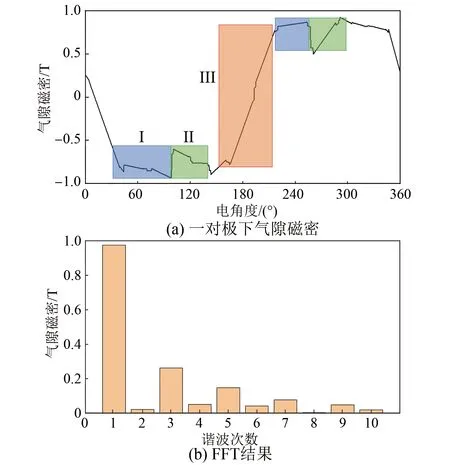
圖6 PMSLM一對極下氣隙磁密及其FFT結果

由于PMSLM的初級是運動的,所以需要對各個時刻齒A齒靴頂部的切向集中力受力情況進行分析計算,仿真計算結果如圖7所示。可知,當齒A左右兩側所受切向電磁力相等時,切向集中力為0;當齒A左右兩側所受切向電磁力不相等時,切向集中力正負變化,產生局部齒槽電磁力波動。

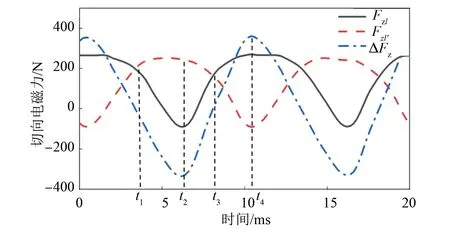
圖7 PMSLM單齒切向集中力曲線

再對齒A所受的局部齒槽電磁力進行仿真計算,結果如圖8所示。可以看出,切向集中力與局部齒槽電磁力的變化趨勢基本一致,因此可認為,切向集中力的變化趨勢可以用來體現局部齒槽電磁力的變化趨勢,為進一步分析建立基礎。

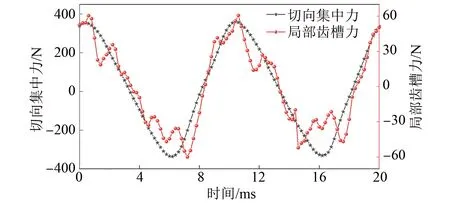
圖8 PMSLM局部齒槽電磁力曲線

在圖7中,將一個周期內的切向電磁力分為t1～t4四個時間結點,其對應的電磁力值分別為0、最小值、0和最大值,圖9為上述各個時刻初級齒A所受電磁力密度的分布圖,可以得到如下結論。

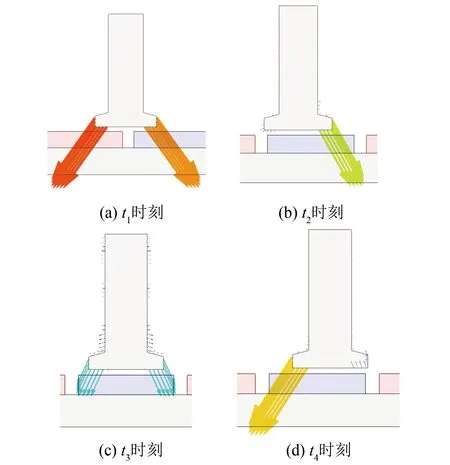
圖9 不同時刻初級齒表面所受電磁力分布

(1)t1時刻,齒A經過永磁體之間的極間區域,齒靴頂部兩端同時受到電磁力作用,且該電磁力關于齒中心線對稱,齒A所受局部齒槽電磁力為0。

(2)t1～t2時間段,PMSLM向右移動,齒靴頂部兩端受到的電磁力不對稱,局部齒槽電磁力在數值上逐漸減小。

(3)t2時刻,Fzl減小到0,齒靴頂部表面電磁力密度主要集中在l′側,齒部受到的局部齒槽電磁力處于波谷位置。

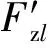
(5)t3時刻,齒中心線和永磁體中心線相重合,齒靴頂部兩端同時受到電磁力作用,且該電磁力關于齒中心線對稱,齒部所受的局部齒槽電磁力為0。

(6)t3～t4時間段,隨著PMSLM的向右移動,齒靴頂部兩端受到的電磁力不對稱,Fzl增大,齒部所受的局部齒槽電磁力變大。

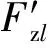
綜上所述,局部齒槽電磁力波動是單齒切向力產生振動的主要原因。當PMSLM初級齒中心線與永磁體中心線或永磁體之間的極間區域中心線相重合時,齒靴頂部兩端所受單齒切向電磁力的合力為0,局部齒槽電磁力也為0;當二者不重合時,齒部磁場畸變,齒靴頂部兩端所受單齒切向電磁力的合力不為0,局部齒槽電磁力也不為0,其值正負波動。

4 PMSLM振動分析

結構系統受到外界激勵產生運動時,將按特定頻率發生自然振動,這個特定的頻率被稱為結構的固有頻率[19]。對于無阻尼單自由系統而言,固有頻率定義如下:

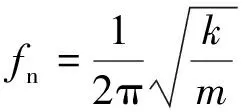
(6)

式中:k為物體的勁度系數;m為物體的質量。

利用ANSYS Workbench仿真平臺,對PMSLM初級的模態進行仿真計算,其結果如圖10所示。

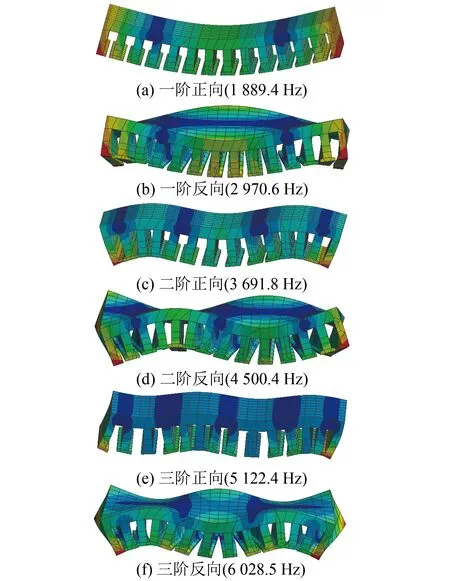
圖10 PMSLM初級模態振型圖

當電機特定階次電磁力波某一頻率分量等于或者接近初級相應模態固有頻率時,初級會發生共振現象[20]。在額定工況下,低頻范圍內的初級各階固有頻率與相應電磁力頻率相差較遠,因此,不會發生共振現象。

空載時,電機在不同電磁力作用下關鍵頻率點的振動加速度如圖11所示。可以看出,兩種電磁力對振動的貢獻既有疊加關系也有抵消關系,僅考慮法向電磁力的作用并不能完全反應電機的振動特性。其次,切向電磁力對振動的貢獻基本可以與法向電磁力比擬[21],因此,切向電磁力也是重要的激振源。

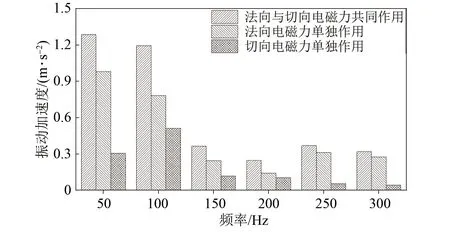
圖11 空載下樣機關鍵頻率點振動加速度仿真結果對比

5 結 語

本文構建了PMSLM模型,根據麥克斯韋應力方程建立了PMSLM單齒切向電磁力數學模型,并對單齒切向電磁力產生振動的原因進行了分析。利用ANSYS Workbench平臺對電機的模態和振動加速度進行計算。結果表明,切向集中力的變化趨勢可以體現局部齒槽電磁力的變化趨勢,局部齒槽電磁力波動是單齒切向電磁力產生振動的主要原因。因此,通過合理調整電機初級齒部磁場分布,能夠有效減小電機的電磁振動,為PMSLM的振動優化提供了參考。