分數槽集中繞組感應電機非主導極次諧波磁動勢抑制方法*

孫春陽, 駱 皓,2, 吳 剛, 胡盛來, 翟長春

(1.南京工程學院 電力工程學院,江蘇 南京 210013;2.江蘇省配電網智能技術與裝備協同創新中心,江蘇 南京 211167)

0 引 言

分數槽集中繞組(FSCW)感應電機憑借其體積小、耗銅量少、轉矩密度大以及能量傳遞效率高等優點,廣泛應用于各個領域。但由于其獨特的繞組排布結構,導致其諧波含量豐富,除去較高繞組系數的主導極次諧波外,部分非主導極次諧波同樣具有較大繞組系數。電機工作時,非主導極次諧波使轉子損耗增大,轉矩脈振增大,極大地影響了FSCW感應電機正常工作時的性能。因此,研究分數槽集中繞組感應電機諧波抑制方法有著十分重要的意義[1-4]。

國內外專家學者對FSCW感應電機諧波抑制方法進行了大量研究,總體可分為內置磁障技術、改變繞組移相技術、改變定子齒槽結構和改變繞組分布效應四個方面[5]。文獻[6-7]提出通過在FSCW定子鐵心中添加磁通屏障以及改變FSCW定子鐵心相鄰兩槽匝數的不等匝繞組結構,有效地減少了低次諧波,但是輸出轉矩受到了影響。文獻[8]通過改變FSCW定子槽口結構有效地抑制了一階繞組次諧波,但其結構局限性較大,難以批量生產。文獻[9-10]通過對Y-Δ混合連接繞組結構的12槽10極永磁電機進行研究,結果表明該結構可有效抑制1次、11次、13次諧波,但對其他次諧波的抑制效果并不理想。相比上述方法,通過添加補償繞組可以抑制特定次諧波,且工藝更簡單,集中繞組結構也更有利于電機模塊化生產。

本文以定子24槽,轉子18槽FSCW繞線式感應電機為例,首先,對FSCW產生的各次諧波磁動勢的分布情況及特點進行分析;然后,分別通過直接補償和移相補償兩種方式添加補償繞組,對電機性能影響較大的7次和5次諧波磁動勢進行抑制;最后,通過理論分析并結合有限元仿真,驗證了所提諧波抑制方法的可行性及有效性。

1 FSCW理論與諧波分析

分數槽集中繞組是指每極每相槽數q小于1,且繞組節距為1的繞組,即:

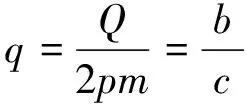
(1)

式中:m為原電機相數;Q為繞組槽數;p為電機極對數;b/c為不可約分的真分數。

若Q與p之間存在最大公約數t,即Q/p=tQ0/tp0,且Q0為相數m的整數倍,則稱槽數為Q0極對數為p0的電機為單元電機,Q槽p極原電機由t個Q0槽p0極單元電機組成[11]。

原電機與其所對應的單元電機具有相同的繞組排布規律與磁動勢分布規律,因此分析Q槽p極感應電機繞組合成磁動勢分布可簡化為分析Q0槽p0極單元電機磁動勢分布規律。

在理想情況下,若定子鐵心齒槽寬度比為1,匝數為Nc的線圈均勻地繞制在單個齒上,通入大小為Im=imcos(ωt)的電流激勵,其在該齒上產生的徑向脈振磁動勢在圓周[-π,π]上的分布可表示為

Fc(θ,t)=

(2)

式(2)經過Fourier極數分解后可表示為

(3)

式中:v為諧波次數;Fam.ν為Nc匝線圈在單個齒上產生的v次諧波磁動勢幅值最大值。

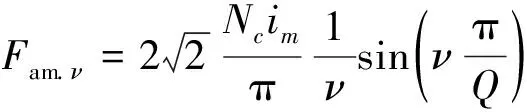
(4)

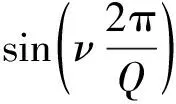
圖1為t=0時刻,單個齒上Nc匝線圈產生的v(v=1,5,7,11)次諧波磁動勢空間分布情況。

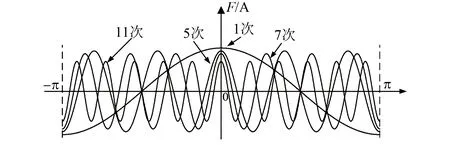
圖1 Nc匝線圈v次諧波磁動勢空間分布

根據式(3)和式(4)可得,t時刻,繞制在單個齒上的Nc匝線圈在圓周上產生的v次諧波磁動勢大小Fc.v(θ,t)為

Fc.v(θ,t)=Fam.vcos(νθ)cos(ωt)

(5)

則單相繞組v次諧波合成磁動勢幅值Fmc.v(θ,t)為

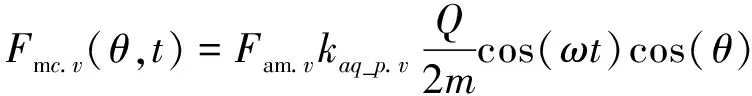
(6)

式中:kaq_p.v為Q槽p極FSCW所產生的v次諧波合成磁動勢的分布系數。

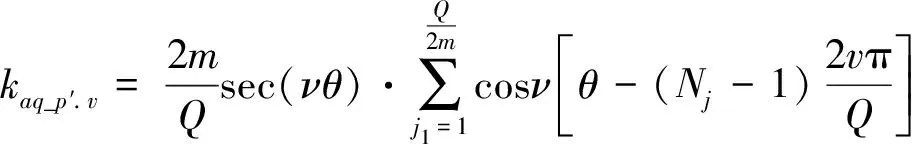
(7)

式中:Nj為相帶劃分后單相繞組對應的齒號。

對于Q槽p極FSCW,各極次諧波磁動勢分布系數按照槽數Q呈周期性分布。對于偶數槽FSCW,不含2k和3k次諧波,且對于v=nQ/2+l和v=nQ/2-l次諧波有著相同的分布系數,即:

kaq.v=nQ/2+l1=kaq.v=nQ/2-l1

(8)

式中:l1=0,1,2,…,(Q-2)/2;n=0,1,2,…。

對于奇數槽FSCW,其諧波磁動勢中不含3k次諧波,且其諧波分布系數滿足:

kaq.v=n(Q+1)/2+l2=kaq.v=n(Q-1)/2-l2

(9)

式中:l2=0,1,2,…,(Q-3)/2;n=0,1,2,…。

FSCW槽數與極數的配合關系滿足:

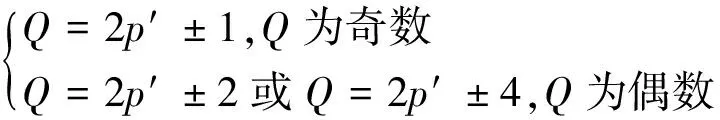
(10)

式中:p′為主導極對數,與諧波次數相對應,p′成對出現且每對p′次諧波的分布系數相同。

當FSCW采用p′次諧波作為基波并確定為極對數時,該次諧波所產生的繞組系數較大。根據式(8)可知,FSCW分布系數成對出現,繞組系數呈周期性變化且逐漸衰減,主導極次諧波合成磁動勢所對應的繞組系數最大。

進一步根據解析法[12]可得三相對稱FSCW在三相對稱激勵下產生的v次諧波合成磁動勢Fm_v.ABC(θ,t)為

Fm_v.ABC(θ,t)=

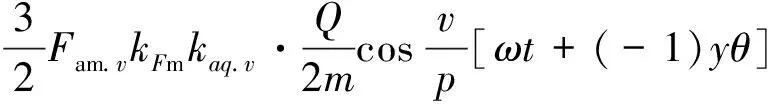
(11)

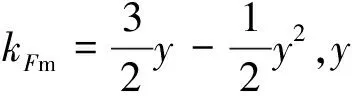
2 特定非主導極次諧波抑制方法

2.1 相帶劃分與空間諧波分布

對于定子24槽轉子18槽的感應電機(24s18r11p),定子24槽的FSCW槽極配合關系滿足Q=2p′±2,其主導極為11和13;轉子18槽的FSCW槽極配合關系滿足Q=2p′±4,其主導極為7和11。定子繞組所產生的11次諧波磁場與轉子繞組產生的11次諧波磁場發生強耦合,作為感應電機的主磁場。24槽定子產生的13次、7次以及其他非主導極次諧波磁場與18槽轉子產生的13次、7次以及其他非主導極次諧波磁場相較于11次諧波磁場產生弱耦合。這些產生弱耦合的磁場是影響電機性能的主要原因,其中13次與7次諧波磁場對電機性能的影響最大[13-14]。

由于定子24槽FSCW中11次和13次為一對主導極對數,具有相同的繞組排布規律以及分布系數,難以單純地抑制13次諧波磁動勢并增強或保持11次諧波磁動勢不變;同理對于18槽定子來說,7和11均為主導極對數,具有相同的繞組排布規律以及分布系數,難以單純地抑制18槽7次諧波磁動勢并增強或保持11次諧波磁動勢不變。

根據三相合成磁動最大原則進行相帶劃分,可以得槽數Q為24,極對數p分別為11、7和5下的相帶分布,如表1所示。本文規定FSCW感應定子24槽p極1號齒中線位置處為機械角0°位置,齒號增大的方向為機械角的正方向。

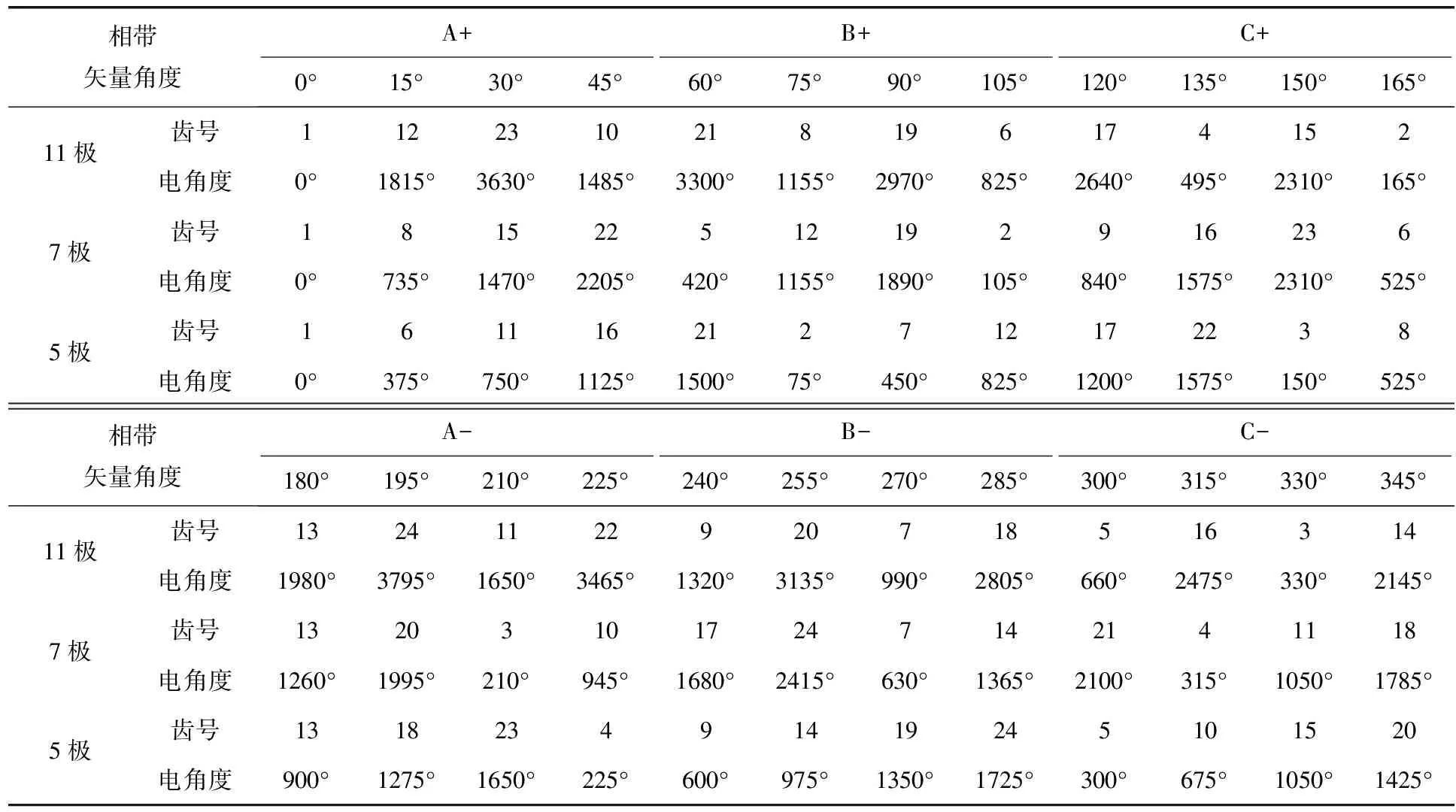
表1 定子24槽相帶劃分

在表1所確定的相帶分布情況下的各相繞組磁動勢星型圖如圖2所示。其中定子24槽FSCW的槽極配合關系滿足Q=2p′±2,每二分之一相槽數為Q/2m,其為偶數,根據槽動勢星型圖的單相繞組磁動勢矢量合成可知,其軸線位置在兩齒之間的槽中線位置處[15]。

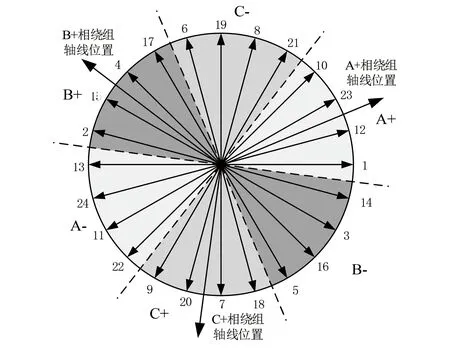
圖2 定子24槽11極FSCW相帶分布與軸線位置

對于轉子18槽FSCW槽極配合關系滿足Q=2p′±4,每二分之一相槽數為Q/2m,其為奇數,根據槽動勢星型圖的單相繞組磁動勢矢量合成可知,其軸線位置在齒中線位置處,如圖3所示。

圖3 轉子18槽7極FSCW相帶分布與軸線位置

根據式(6)可得A相繞組在不同極對數下v次諧波合成磁動勢在圓周上的分布為

FA_p.v(θ,t)=

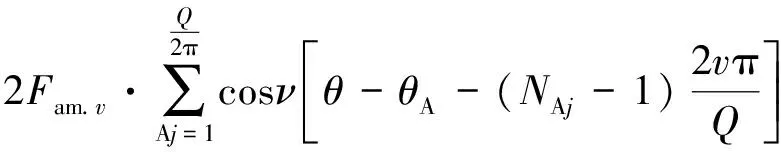
(12)

式中:θA為A相繞組機械角度下的軸線位置;NAj為按照p=11、7、5進行相帶劃分后的A相繞組第Aj個齒所對應的齒號。

同理可得B相,C相所對應的v次諧波合成磁動勢為

FB_p.v(θ,t)=

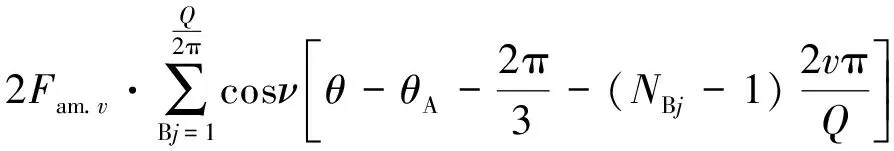
(13)

FC_p.v(θ,t)=

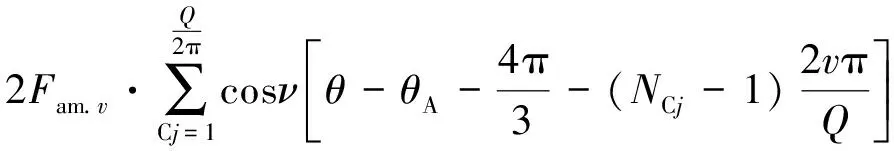
(14)

根據式(12),可得定子24槽不同極對數下單相繞組各次(v=1,5,7,11)諧波磁動勢分布情況如圖4所示,根據式(8)可知,槽數Q為24時,11次和13次諧波的分布系數相同,即其在軸線位置處時,均同時處于波峰或者波谷位置。同理,7次與17次諧波、5次與19次諧波、1次與23次諧波均具有相同規律,故本文只畫出極對數為1,5,7,11時的諧波磁動勢分布[16-17]。

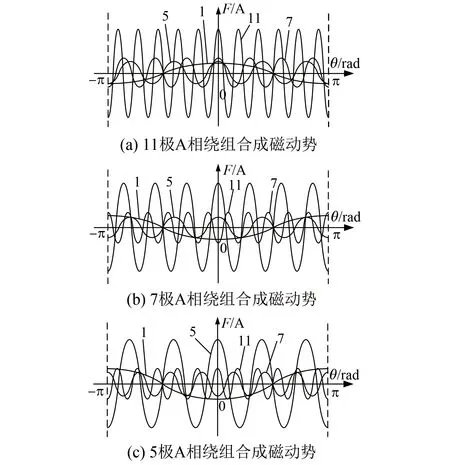
圖4 定子24槽不同極數下各極次諧波分布

根據圖4(a)與式(12)可知,定子24槽11極FSCW,在軸線位置各次(v=11,7,5,1)諧波磁動勢隨時間的變化時均同時處于波峰或波谷位置;同理根據圖4(b)和式(12)可知,定子24槽7極FSCW在軸線位置處11次和5次諧波磁動勢隨時間變化時,均同時處于波峰或波谷位置,與7次和5次諧波磁動勢在波形圖中的位置相反。定子24槽7極FSCW和轉子18槽FSCW各極次諧波在軸線位置處的分布情況同理。

根據式(6)和式(11)可知,無論分數槽集中繞組感應電機極對數為多少,其定子繞組產生的各次諧波三相合成磁動勢的角頻率以及各相繞組上各次諧波磁動勢的脈振頻率相同。進一步可得當采用Q槽p極分數槽集中繞組排布方式時,其p次諧波磁動勢的繞組系數最大,將其作為補償繞組便可以最少的耗銅量抑制該次諧波磁動勢。

2.2 直接補償法

若以24槽11極FSCW為原繞組,其中11次和13次諧波產生的次合成磁動勢最大。且在軸線位置處,11極和7極諧波磁動勢均同時處于波峰或波谷;以24槽7極FSCW為補償繞組,其軸線位置處11極和7極諧波磁動勢分別處于波峰和波谷位置。

若原繞組相帶分布以及各相繞組排布確定,通過調整補償繞組和原繞組各相軸線相對位置,即可對特定次諧波進行抑制,原繞組與補償繞組各相軸線位置滿足關系:

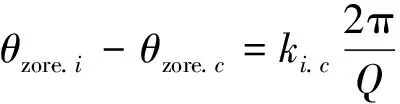
(15)

式中:θzore.i為原繞組各相繞組軸線位置的機械角度;θzore.c為補償繞組與原繞組所對應的同相繞組的軸線位置的機械角度,ki.c=0,1,2,…,Q。

若原繞組和補償繞組的各相繞組串聯,當ki.c取12時,原繞組7次諧波磁動勢的抑制效果最好,耗銅量最少,且可以適當增強原繞組11次諧波磁動勢。此時原繞組和補償繞組的各相軸線位置相差180°機械角度,即原繞組A+、B+、C+三相位置與補償繞組A-、B-、C-三相軸線位置在機械角度上相同。所對應的原繞組和補償繞組的繞組磁動勢星型圖[18]如圖5所示。

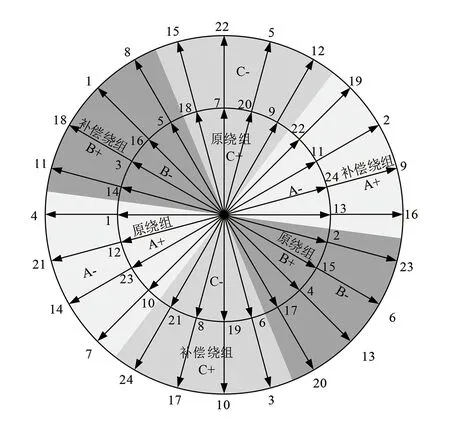
圖5 直接法補償繞組與原繞組磁動勢星型圖

結合式(12)、式(13)和式(14)可知,若要通過補償繞組將原繞組所產生的7次諧波磁動勢完全抑制,各相繞組均應滿足條件:

|FA_com.7(θ,t)|-|FA_in.7(θ,t)|≈0

(16)

進一步可由式(16)得原繞組和補償繞組的各繞組線圈匝數比kcom.v為

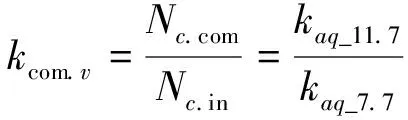
(17)

式中:Nc.in為原繞組線圈匝數;Nc.com為補償繞組線圈匝數。

由于繞組線圈匝數必須為整數,故當原繞組匝數一定時,補償繞組線圈匝數需取與其匝數比和原繞組匝數乘積相鄰的整數。

2.3 移相補償法

根據圖4可知,定子24槽11極FSCW與24槽5極FSCW在任意時刻所產生11次諧波槽動勢和5次諧波槽動勢在軸線位置處均同時處于波峰或波谷位置,而對于直接補償法,當采用補償繞組抑制5次諧波時,其原繞組11次諧波合成磁動勢必然會受到抑制。

FSCW感應電機各相繞組在t=0時刻所產生的11次諧波磁動勢各波峰與和5次諧波磁動勢各波谷之間的電角度之差θΔ_11pe.5t為

(18)

同理,在t=0時刻所產生的11次諧波磁動勢各波谷與5次諧波磁動勢各波峰之間的電角度之差θΔ_11t.5pe為

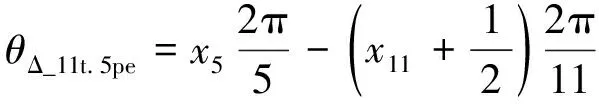
(19)

式(18)和式(19)所得數值的正負表示11和5次諧波磁動勢各個波峰波谷間的超前或滯后關系,且兩式絕對值的最小值滿足關系:

|θΔ_5pe.11t|min=|θΔ_11pe.5t|min

(20)

按照表1相帶劃分繞制的11極原繞組在機械角度上的軸線位置為θzore.main,5極補償繞組機械角度上的軸線位置為θzore.com1。根據圖4(b)可知,24槽5極FSCW所產生的各次諧波磁動勢在θzore.com1±π區間內,關于θ=θzore.com1軸對稱,關于θzore.com1±π/2中心對稱。在[0～2π]機械角度中存在四個位置使得24槽5極FSCW所產生的11次諧波磁動勢的各波峰或波谷的位置與5次諧波磁動勢的波谷或波峰的位置電角度之差的絕對值最小,且這四個位置關于軸線位置對稱。

24槽5極FSCW從正方向計算產生的11次諧波磁動勢波峰與5次諧波磁動勢波谷的電角度之差的絕對值最小時的峰谷角度差θ+Δ_11pe.5t為

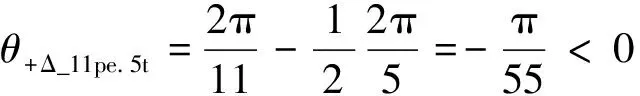
(21)

根據式(21)可知,沿其軸線位置正方向,11次諧波磁動勢的波峰超前5次諧波磁動勢的波谷。并且其正方向上第一次出現θ+Δ_11p.5t絕對值最小的位置滿足:

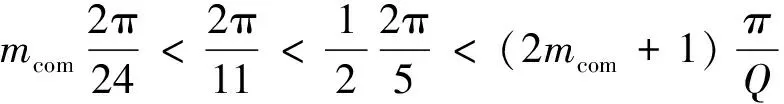
(22)

式中:mcom(2π/24)為各定子鐵心槽中線位置的機械角度;(2mcom+1)π/Q為各定子齒中線位置的機械角度;mcom=0,1,2,…,Q為齒數系數,當mcom等于2時,式(22)成立。

若采用兩組繞線方式和線圈匝數完全相同的24槽5極FSCW共同組成補償繞組,第一組24槽5極FSCW稱為補償繞組com1,第二組24槽5極FSCW稱為補償繞組com2。當補償繞組com1與補償繞組com2軸線在正方向位置上同相軸線位置θzore.com相差的槽數為2mcom時,補償繞組com1和補償繞組com2所合成的v次諧波合成磁動勢的軸線位置θzore.com相較于補償繞組com1軸線位置θzore.com1在正方向上移動了mcom(2π/24)。即通過兩組完全相同的補償繞組可將單組補償繞組軸線位置從兩相鄰齒對稱中線位置處移至單個齒中線位置處,且不會破壞集中繞組的各繞組線圈間高獨立的優點。

當mcom等于2時對應的添加雙組補償繞組com1和com2的磁動勢星型圖如圖6所示,雙組補償繞組com1與com2合成的11次諧波磁動勢與5次諧波磁動勢在t=0時刻的空間分布情況如圖7所示。

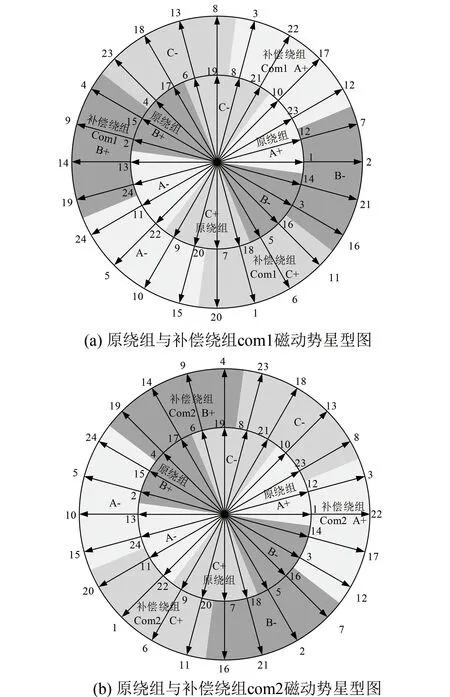
圖6 移相法補償繞組磁動勢星型圖

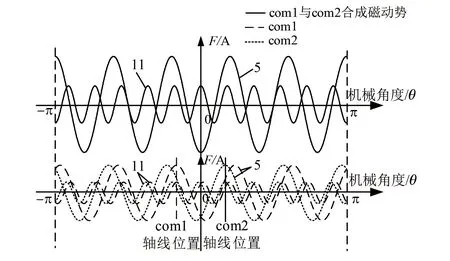
圖7 補償繞組com1和com2合成磁動勢分布

雙補償繞組合成磁動勢的A相繞組,其軸線位置為

(23)

雙組補償繞組產生的主導極次諧波和擬抑制極的諧波在其軸線位置處分別處于波峰位置和波谷位置。

其雙組補償繞組產生的v次諧波合成的單相繞組磁動勢在圓周上的分布為

Fm.com.v(θ,t)=

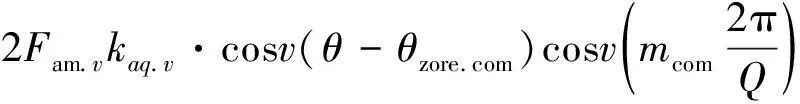
(24)

進一步可知,存在mcom使得t=0時刻在雙補償繞組軸線位置處11次合成磁動勢為正值,且擬被抑制的7次諧波合成磁動勢幅值為負的最小值,此時當原繞組與雙組補償繞組各相軸線位置對齊時,即可通過最少的耗銅量在盡可能抑制7次諧波合成磁動勢的同時,適當地增強11次諧波合成磁動勢。

此時原繞組和雙組補償繞組所產生的5次諧波合成磁動勢滿足關系:

|FA_11.5(θ,t)|-|FA_com.5(θ,t)|≈0

(25)

由式(25)可得雙組補償繞組的匝數Nc.com為

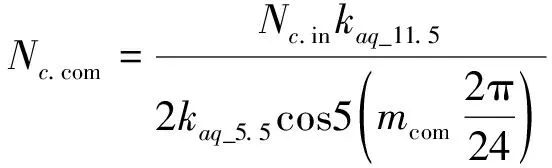
(26)

3 仿真分析

本文以一臺定轉子均為分數槽集中繞組的感應電機為研究對象利用Maxwell軟件建立有限元二維模型,其基礎參數設置如表2所示。根據2.2節直接補償法(直接法)與2.3節移相補償法(移相法)分別在定子24槽11極原繞組的基礎上設置補償繞組,原繞組和補償繞組的參數如表3所示,其中補償繞組與原繞組的連接方式均為串聯,添加補償繞組后控制控制方式不變。

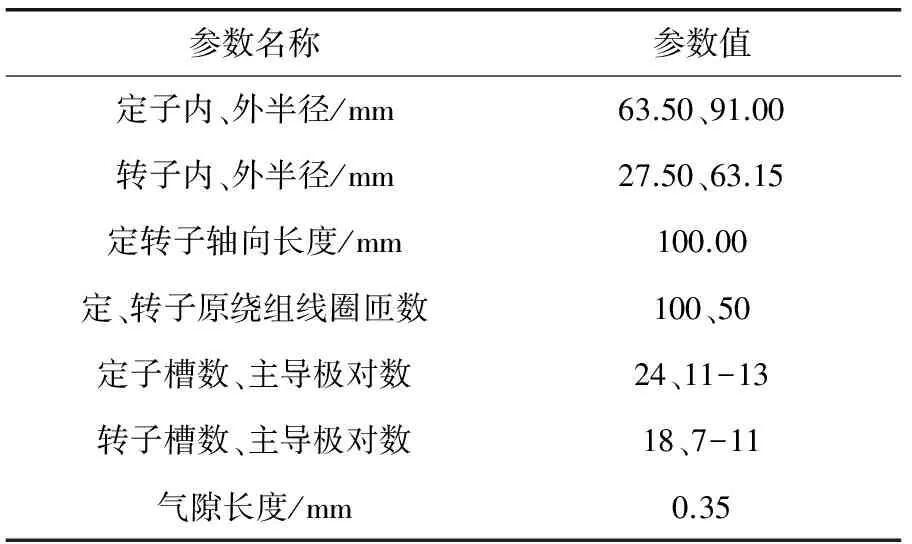
表2 定轉子分數槽集中繞組感應電機參數

表3 原繞組與補償繞組參數

3.1 氣隙磁密分析

分別對定子24槽11極原繞組和添加補償繞組后的繞組施加50 Hz三相對稱電流激勵,其表達式為

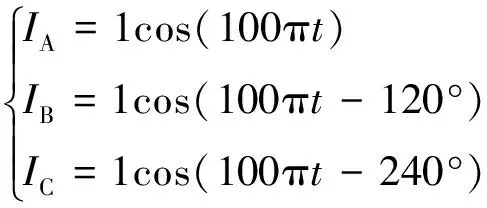
(27)

當轉子側無激勵且轉速為零時,不同情況下得到氣隙磁密如圖8所示。

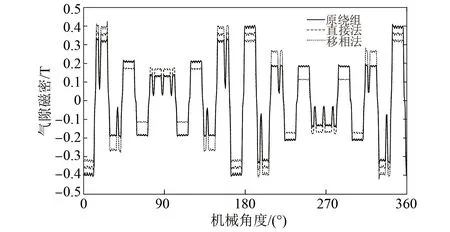
圖8 不同諧波抑制方法下氣隙磁密

對圖9中不同繞組下的氣隙磁密進行FFT頻譜分析,由于偶數槽三相對稱FSCW所產生的3k和2k極次諧波磁動勢在空間上相互抵消為零,且各次諧波周期性分布逐漸減小,根據式(8)可知v=nQ/2+1和v=nQ/2-1次諧波具有相同的分布系數,因此圖9中只展示了v=1,5,7,11,13,17,19,23次諧波下的頻譜分析結果。

圖9 氣隙磁密頻譜分析

根據圖8可知,針對7次和5次諧波進行抑制的補償繞組,對11次諧波均有增強作用。采用直接法補償繞組抑制7次諧波,氣隙磁密所含的7次諧波減少了78.22%,11次諧波增強了3.19%;采用移相法添加補償繞組抑制5次諧波,氣隙磁密所含的5次諧波磁密減少了96.52%,主導極11次諧波磁密增加了2.22%。

3.2 轉子感應電動勢

FSCW感應電機定轉子間感應電動勢角頻率關系可以表示為

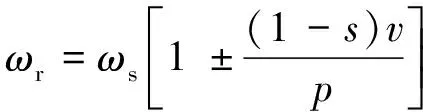
(28)

式中:ωr為轉子感應電動勢頻率;ωs為定子電流激勵角頻率,這里取值為50;s為轉差。

將轉子轉速設置成轉差為0.3時所對應的轉速,測量18槽轉子側不同繞線方式下的A相感應電動勢,結果如圖10所示。

圖10 不同諧波抑制方法下轉子電動勢

對原繞組、按照直接法和移相法添加補償繞組后轉子轉速在0.3轉差下的感應電動勢進行FFT頻譜分析,取未添加補償繞組的原繞組中轉子感應電動勢幅值最大的前五次諧波分量,如圖11所示,依次為72.72、15、91.36、53.18、34.09 Hz。

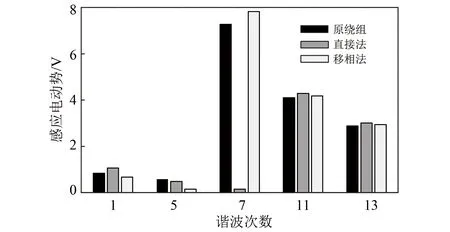
圖11 轉子感應電動勢諧波分析

根據式(28)可知,轉子側感應電動勢頻譜分析所得感應電動勢幅值最大的五次諧波分量分別為7,11,13,1,5次。對于24槽定子側原繞組,由于18槽轉子主導極對數為7和11,且7極繞組系數大于11極繞組系數,故轉子側繞組7極感應磁動勢分量最大。定子側11對極和13對極為主導對數,繞組系數最大,故轉子側產生11級和13極的感應電動勢僅低于7極感應電動勢。

3.3 電磁轉矩

保持24槽定子三相對稱電流激勵不變,對轉子施加三相對稱電壓激勵,幅值為50 V,頻率為15 Hz,將轉子轉速設置成轉差為0.3時所對應的轉速,得到原繞組、按照直接法和移相法添加補償繞組后的轉矩如圖12所示。

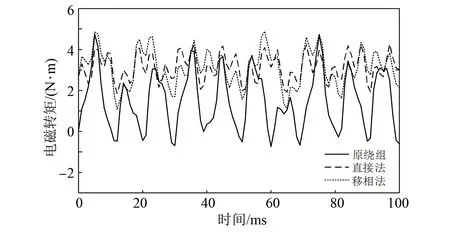
圖12 轉子感應電動勢諧波分析

原繞組和添加補償繞組后的轉矩脈動與平均轉矩如表4所示。由圖12和表4可知,直接法和移相法均可有效提高轉矩且減小轉矩波動。其中直接法對原繞組產生的7次諧波進行抑制,平均轉矩提高了53.5%,轉矩波動減少了56.2%;移相法對原繞組產生的5次諧波進行抑制,平均轉矩提高了53.4%,轉矩波動減少了30.3%。由于原繞組中7次諧波繞組系數大于5次諧波繞組系數,故通過直接法抑制7次諧波對改善電機轉矩波動的效果更明顯。

表4 原繞組與補償繞組平均轉矩與轉矩波動 N·m

3.4 耗銅量與諧波抑制效果

通過直接法抑制7次諧波,在0.3轉差的轉速下轉子側7次感應電動勢下降了97.98%,相較于未添加補償繞組的原繞組,耗銅量提高了22%;通過移相法抑制5次諧波,在0.3轉差的轉速下轉子側5次感應電動勢下降了73.82%,相較于未添加補償繞組的原繞組,耗銅量提高了14%。通過直接法與移相法抑制非主導極次諧波效果與相對于未設置補償繞組的原繞組耗銅增加量如表5所示。

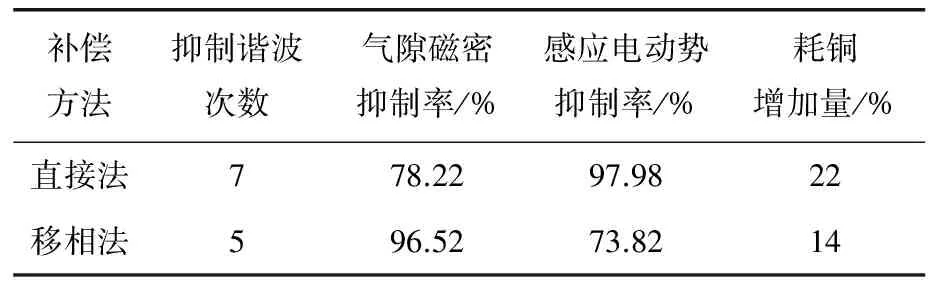
表5 補償繞組諧波抑制效果與耗銅量

通過表5可知,直接法和移相法均對非主導極次諧波有抑制效果,其中直接法適用于軸線位置處主導極次諧波與擬抑制的諧波空間相位差為0°的情況;移相法適用于軸線位置處主導極次諧波與擬抑制的諧波空間相位差為180°的情況。

若電機原繞組槽滿率相對較低,電機繞組槽內空間留有一定裕度時,可考慮直接法添加補償繞組;若電機原繞組槽滿率相對較高,槽內剩余空間較小,此時需要根據實際情況在保證原繞組與補償繞組的匝數比保持在最佳匝數比附近的前提下適當地減少原始繞組匝數和補償繞組匝數來減少總匝數,雖然減少原繞組匝數不可避免會導致主導極次諧波的幅值減小,但是相對應地諧波后電機整體性能會有所提升。

以原繞組和補償繞組均采用線徑0.74 mm的導線為例,在保持原繞組匝數不變和總匝數不變兩種情況下諧波電動勢含量以及槽滿率對比如表6所示。

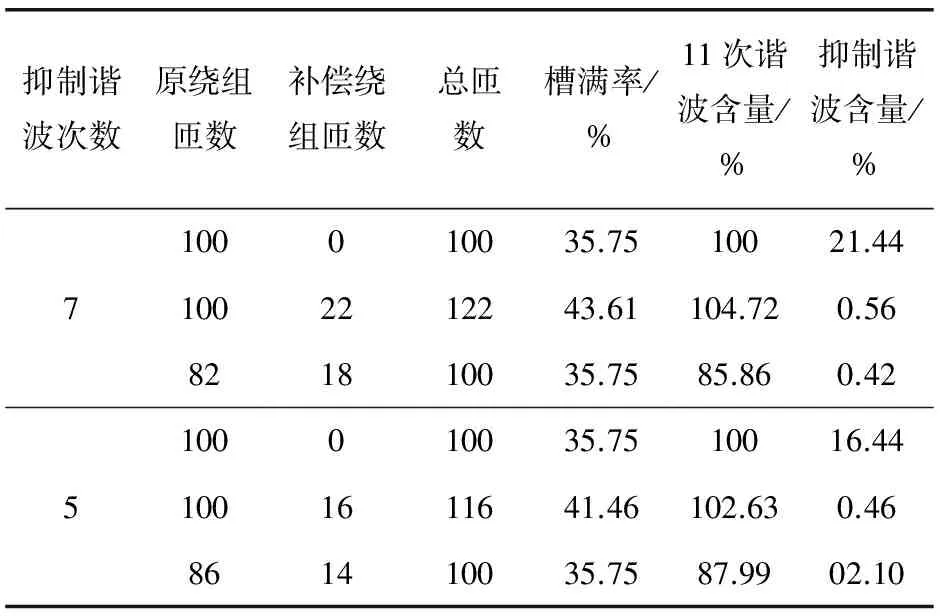
表6 不同槽滿率下諧波抑制效果

4 結 語

本文以一臺定子24槽11極,轉子18槽7極FSCW感應電機為例分析了其定子側FSCW產生的各極次諧波分布規律,并設計了直接補償法和移相補償法兩種添加補償繞組的方法,用以抑制高分量非主導極次諧波,通過理論分析和有限元仿真驗證了兩種方法的有效性與可行性。分析表明:

(1) 直接補償法適用于槽數一定的FSCW,極對數分別為主導極和擬抑制諧波次數時各繞組軸線位置處任意時刻產生的主導極次諧波磁動勢與擬抑制的諧波磁動勢不同時為波峰值或波谷值的情況。該方法可以在抑制非主導極次諧波磁動勢的同時適當地增加主導極次諧波磁動勢的幅值。

(2) 移相補償法適用于槽數一定的FSCW,極對數分別為主導極和擬抑制諧波次數時各繞組軸線位置處任意時刻產生的主導極次諧波磁動勢與擬抑制的諧波磁動勢同時為波峰值或波谷值的情況。該方法可以在抑制非主導極次諧波磁動勢的同時適當地增加主導極次諧波磁動勢的幅值。

(3) 添加補償繞組的方法可以有效抑制FSCW產生的非主導極次諧波并適當增加主導極次諧波含量,減小轉矩脈動,但是在一定程度上增加了耗銅量,同時增加了電機槽滿率,當原始電機繞組槽滿率較高時,需要適當減少原始電機繞組匝數來保證槽內有足夠空間添加補償繞組。

(4) 補償繞組仍采用FSCW結構與原繞組串聯,可保持集中繞組高齒間獨立性的優點,加工制造難度與原FSCW感應電機難度基本相同。