不同注漿壓力下采空區漿液擴散規律研究

程立朝，路 濱，李新旺，郝云德，龍 杭，王海璇

（1.河北工程大學礦業與測繪工程學院，河北邯鄲 056038；2.河北工程大學 河北省高校煤炭資源開發與建設應用技術研發中心，河北 邯鄲 056038；3.河北工程大學 邯鄲市煤基固廢規模化利用技術創新中心，河北 邯鄲 056038）

0 引 言

煤炭開采規模的不斷擴大，導致地表形成大面積的沉陷區，地表生態環境出現破壞[1]。采空區充填注漿是近年發展起來的生態保護性開采技術，采空區注漿加固治理是一種通過地面打孔滲透注漿實現采空區沉降改善的治理工藝[2-3]。通過將特定性質的材料配制成漿液，借由地面提前鉆孔布設的注漿管，在一定的壓力下將漿液注入采空區地基矸石堆體內，通過漿液的滲透實現采空區充填。隨后，漿液經過膠凝或固化處理，促使地基的物理力學性質得到改善，從而達到加固采空區地表地基的目的。滲透注漿作為一種有效的施工方法，在工程領域具有廣泛的應用前景。

在對采空區滲透注漿擴散規律的相關研究中，國內外學者已經進行了大量的工作。楊志全[4]等基于賓漢姆流體漿液時變性的流變方程和滲流運動過程，得到了漿液時變性對注漿擴散半徑的影響規律；阮文軍[5]通過大量的試驗研究，建立了不同流形漿液的粘度時變性方程，在此基礎上獲得了穩定的水泥漿液注漿擴散模型；李術才[6]等研究了基于黏度時變性的雙液漿液擴散運移機制；黃河飛[7]利用COMSOL 探究了水灰比、注漿壓力等對漿液擴散滲透規律的影響；尚宏波[8]等利用COMSOL 構建了地面下含水層帷幕注漿漿液擴散物理模型，討論了在動水條件下漿液擴散范圍影響因素；劉洋[9]等通過COMSOL 建立在巖石裂隙中注漿擴散模型，研究了粘度及裂隙粗糙度對擴散半徑的影響；錢自衛[10]等基于達西定律推算出全新的滲透注漿漿液擴散半徑公式；張宏圖[11]等基于COMSOL 中流固耦合模塊，研究了不同注漿壓力下瓦斯抽采水泥砂漿封孔注漿擴散模型，討論了砂漿黏度變化對注漿影響；王慶磊[12]等基于滲濾效應的多孔介質探究了低滲透率賓漢姆漿液滲透擴散規律；Maghous 等[13]分析了水泥漿液在多孔介質中徑向流動時出現的過濾現象；楊文才研究獲得了基于漿液自重的牛頓、賓漢姆和冪律流體的球形滲透注漿理論[14]；朱明聽[15]利用CFD 中的COMSOL 軟件，在單一裂隙注漿擴散為背景下，采用理論分析與數值模擬相結合的方法，通過控制變量包括注漿壓力、注漿速度和裂隙開度等，模擬了漿液擴散運移和注漿壓力在不同流場下的分布規律。這些學者的研究工作豐富了采空區滲透注漿擴散規律的理論基礎。他們通過試驗、理論推導和數值模擬等手段，對不同類型的注漿流體和工程情況進行了深入的研究。這些研究成果對于優化滲透注漿工程的設計參數、預測注漿效果，以及提高工程施工質量，具有重要意義。通過進一步深入研究和探索，能夠更好地理解和應用采空區滲透注漿擴散規律，提升了采空區治理的效果和安全性。

當前國內外學者在注漿漿液擴散規律方面展開了大量的研究，但多以Magg 球狀擴散理論和達西定律為主，對于在淺埋深大面積采空區注漿工程中，注漿在雜亂矸石堆中擴散規律鮮有研究。因此，本文旨在以賓漢姆粉煤灰漿液為研究基礎，考慮賓漢姆粉煤灰漿液的黏度特性、流動性以及與土層矸石堆的相互作用等因素，對其在采空區內復雜的流動擴散規律進行研究，以提供一定的理論基礎來指導實際的注漿工程。

1 采空區內滲透注漿漿液擴散物理模型

1.1 水泥粉煤灰漿液流變方程

在對采空區內水泥粉煤灰漿液滲透擴散機理進行研究時，可對采空區提出以下假設。

（1）注漿治理的采空區內被注煤矸石和冒落巖石散體是一種均勻和各向同性的多孔介質，被注散體各個方向性質相同。

（2）水泥粉煤灰漿液可被視為不可壓縮的流體，同時其自身也是均質且各向同性。此外，漿液粘度隨時間發生變化，這種變化關系可以用指數函數來描述。而在整個注漿過程中，水泥粉煤灰漿液的屈服應力整體上保持不變。

（3）采用填壓法進行注漿，通過注漿管口將水泥粉煤灰漿液注入采空區被注介質內。

（4）漿液流動速度較小，除了在注漿孔周圍局部區域，漿液的流態呈現紊流狀態外，其余部分表現為層流。

以Brinkman 方程為研究基礎，認為水泥粉煤灰漿液遵循賓漢姆流體流動特性，滿足流變方程：

式中：τ 為剪切應力，Pa；τ0為屈服應力，Pa；μn為塑性粘度，Pa·S；γ 為剪切速率（γ=-），S-1。

水泥粉煤灰漿液的粘度時變性規律為：

式中：μno為水泥粉煤灰漿液初始粘度值，Pa·s；μn為漿液時變粘度值，Pa·S；k 為粘度時變系數；t為注漿時間，S。

式（1）、式（2）聯立可得水泥粉煤灰漿液考慮粘度時變性狀況下的流變方程：

1.2 賓漢姆流體滲流擴散規律

當研究賓漢姆流體在圓管中的層流流動時，可以考慮在圓管內取一段以管軸為對稱軸的流體柱，其長度取dl，半徑取r＜r0，r0為圓管半徑，如圖1所示。

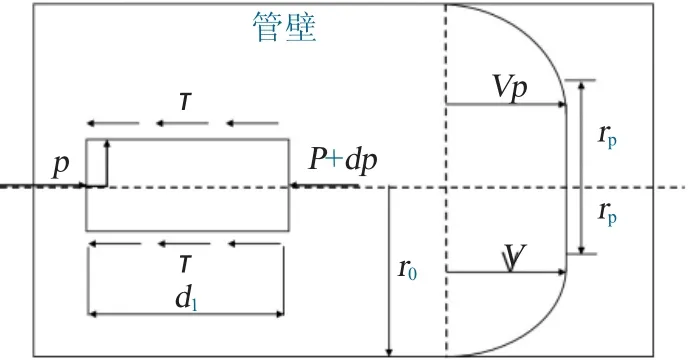
圖1 水泥粉煤灰漿液在圓管中的流動示意Fig.1 Flowdiagram of cement fly ash slurry in circular tube

在不考慮重力對其流動影響下，該流體柱力學平衡公式為：

流體柱微元部dl 兩端的壓力分別為p+dp 和p，兩端壓差為dp。流體柱元素表面上受剪切應力為τ，其方向向左與流速方向相反。可以得到剪應力τ：

在柱元素表面上，剪切應力τ 與柱元素半徑r和壓力梯度dp/dl 的乘積成正比，但符號相反。將上式帶入賓漢姆流變方程可得水泥粉煤灰漿液的滲流運動方程為：

式中：v 為水泥粉煤灰漿液滲流速度，m/s；K 為地層滲透系數；α 為水的滲透系數。

由v=q/A 可得：

積分可得：

根據邊界條件p=p1時，l=l0；p=p0時，l=l0可以計算出漿液擴散半徑：

2 采空區注漿漿液擴散數值模擬

2.1 控制方程

采空區注漿漿液擴散過程本質上是水泥粉煤灰漿液驅替其他物質的過程。采空區內有大量冒落的矸石和其他巖體，其松散堆積體可以視為多孔介質，孔隙率一般都比較大，故選擇COMSOL 中的Brinkman 方程對采空區內漿液擴散效果進行模擬。

（1）運動控制方程。

Brinkman 方程是一種在多孔介質流動中考慮滲流和粘流耦合效應的方程。該方程描述了在多孔介質中流動的動量守恒和連續性。第一項表示速度的散度，第二項表示速度的擴散，第三項表示速度的粘性耗散，第四項表示壓力梯度，最后一項表示外部施加的力場。

式中：εp為孔隙率；K 為滲透系數；Qm為流量。

2.2 模型建立及邊界設定

以邯邢地區淺埋深煤層采空區為研究背景，數值模擬模型設定為100 m×100 m×4 m，工作面平均厚度為4 m，注漿管直徑為10 cm，注漿管位于模型的中心位置，整個模型采取自由形三角形單元進行劃分，為了提高計算的精確度，在注漿管口處網格進行加密處理。網格劃分如圖2 所示。

圖2 模型概圖Fig.2 Model overview

模型的四周邊界均為無滑移，入口邊界設定為壓力入口，注漿壓力為p_in=0.2 MPa，出口邊界為p=0，冒落矸石堆孔隙率為0.302 6，水泥粉煤灰的密度為1 342 kg/m3，數值模擬參數見表1。

表1 計算參數Table 1 Calculation parameters

水泥粉煤灰漿液的時變性曲線如圖3 所示。

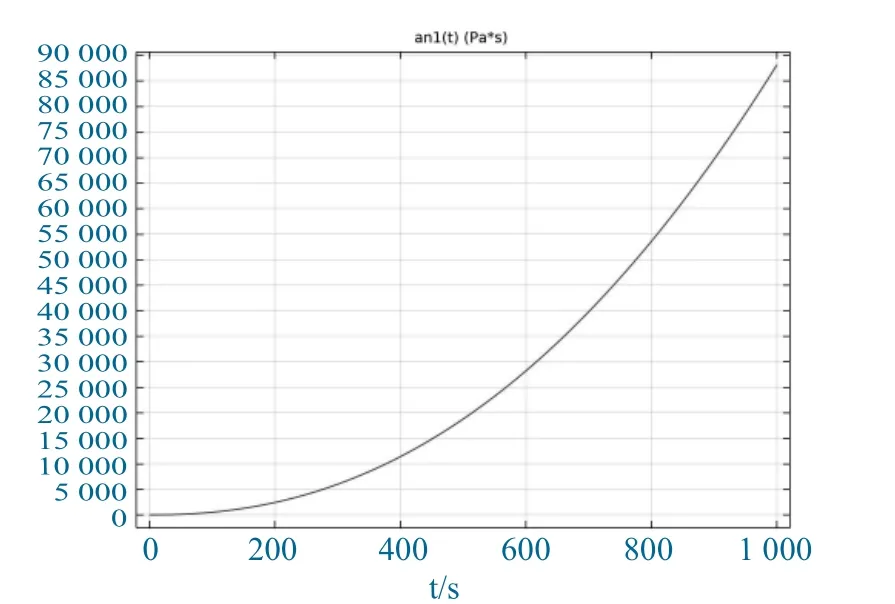
圖3 粘度時變性曲線Fig.3 Viscosity time-varying curve

2.3 漿液擴散數值模擬結果和分析

在用COMSOL MULTIPHYSICS 模擬水泥粉煤灰漿液在采空區冒落矸石堆中流動擴散規律時，可以用濃度指標來表示注漿漿液的擴散范圍，可以認為濃度達到0.1 以上時，漿液可以到達這些地方，即為漿液擴散區域。

2.3.1 注漿時間對擴散半徑的影響

在進行注漿時，由于水泥粉煤灰漿液具有黏度時變性，故研究漿液擴散隨時間變化的趨勢，截取不同時間點的擴散形態圖，其它參數保持不變。模擬結果如圖4 所示。

圖4 注漿時間對漿液擴散距離的影響Fig.4 Effect of grouting time on slurry diffusion distance

觀察結果表明，水泥粉煤灰漿液在模擬實驗中以注漿管為中心以圓狀進行擴散，這可以歸因于對被注入的矸石堆采用各向同性假設。根據這個假設，漿液從注漿孔流出后在各個方向上的擴散距離是相等的，因此導致了漿液以相同速率擴散至各個方向。在以下描述中，圓形區域表示了漿液在采空區內的擴散距離：對于注漿時間為2 h 的情況（圖4a），漿液的擴散距離達到了6.93 m；對于注漿時間為4 h 的情況（圖4b），擴散距離增至8.27 m；對于注漿時間為6 h 的情況（圖4c），漿液的擴散距離為9.15 m；在注漿時間為8 h 的情況下（圖4d），漿液的擴散距離擴展至9.95 m。

上述數據可以整理成圖5，顯示了不同注漿時間下漿液擴散距離的變化趨勢。這一趨勢清晰地展示了漿液擴散隨著注漿時間變化的關系。

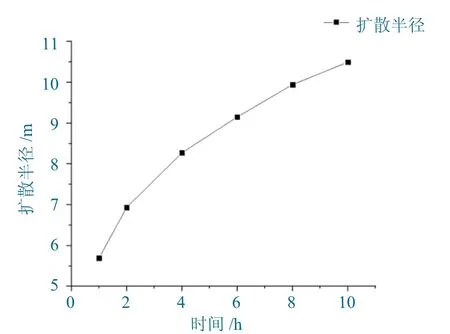
圖5 擴散距離與時間的關系Fig.5 The relationship between diffusion distance and time

由圖5 可知：

（1）在進行采空區注漿加固的初期，由于采空區內孔隙率較大，隨著注漿時間的增大，水泥粉煤灰漿液擴散半徑也隨之增加。

（2）漿液的流動擴散速度隨著漿液擴散的位置越遠而逐漸減小，這是因為漿液的粘度隨著時間的增加而增大，到一定時刻，漿液的粘度無限大后，漿液停止流動。因此對于采空區注漿加固來說，注漿時間對于水泥粉煤灰漿液擴散半徑的影響主要取決于漿液何時凝固。

2.3.2 注漿壓力對擴散半徑的影響

注漿壓力是指在注漿過程中施加到漿液上的力，使漿液能夠克服地下介質的阻力，滲透進入孔隙或裂縫中。注漿壓力的大小對注漿效果具有重要影響，過低的壓力可能導致漿液無法充分滲透，而過高的壓力則可能引起地下介質的破壞或漿液四溢，造成漿液浪費。查閱有關規定，此次模擬注漿壓力主要選取0.2～1 MPa。

在保證其他條件不變的情況下，改變注漿壓力。模擬結果如圖6 所示。

圖6 注漿壓力對漿液擴散距離的影響Fig.6 Effect of grouting pressure on slurry diffusion distance

圖6（a）展示了在0.2 MPa 注漿壓力下，漿液的擴散情況，結果顯示漿液最終的擴散范圍達到10.01 m；而圖6（b）呈現了在0.5 MPa 注漿壓力下，漿液在介質中的擴散情況，相應擴散距離為14.51 m；圖6（c）呈現了在1 MPa 注漿壓力下漿液的擴散狀況，漿液最終的擴散距離達到18.96 m。圖中圓圈內區域為漿液的最大流速區域，而圓圈外區域則代表漿液流速為零的區域。

由圖6 可以看出：

（1）在相同的注漿材料、冒落矸石堆孔隙率下，不同情況的漿液擴散半徑隨著注漿壓力增大而增大。

（2）注漿壓力的增加會導致漿液的初始流動速度增大。當水泥粉煤灰漿液在采空區內矸石堆孔隙流動時，克服孔隙水壓力和顆粒之間的阻力等會導致漿液動能損失，從而引起流速逐漸減小。當漿液的初始流動速度較大時，這種流速減緩的趨勢較為緩和，因此在采空區內的擴散半徑越大。

為研究在注漿過程中，不同區域壓力的變化，在離注漿管口1、2、3 m 的高度布設3 條注漿壓力測線，線上均勻布設監測點，如圖7 所示。不同距離壓力變化如圖8 所示。

圖7 監測點布設Fig.7 layout of monitoring spot

圖8 不同距離壓力變化Fig.8 Pressure variation at different heights

從圖8 可以看出，在同一深度，壓力值在注漿管中心位置，同一高度壓力在注漿管中心附近壓力值最大，壓力隨著水泥粉煤灰漿液擴散范圍的增大而向邊界遞減，在深度越大的位置，注漿滲透壓力的值越小，變化幅度越小，距離注漿管越遠的地方壓力增加速度越慢，說明注漿壓力對距離越遠的測點影響越弱。

3 結 論

（1）水泥粉煤灰漿液屬于賓漢姆流體，在注漿過程中其粘度存在時變性，粘度隨時間發生指數型變化。

（2）水泥粉煤灰漿液在采空區內擴散形態最初呈球體變化至圓柱體；漿液擴散半徑隨著注漿時間增加而增大，且變化速度隨著漿液粘度的增大而減小。

（3）注漿擴散距離隨著時間的增大而增加，由于粘度時變性的影響，擴散速度隨之減少。注漿壓力對漿液擴散范圍影響較為明顯，隨著注漿壓力的增大，漿液擴散距離隨之增大，可以得出，在前期注漿的時候可以提供較小的壓力，可適當地提高注漿壓力來提高注漿效率。