深部軟巖巷道圍巖變形機理研究

焦若珂

（潞安化工集團有限公司 古城煤礦，山西 長治 046000）

0 引 言

隨著我國經濟的持續發展，煤炭資源的需求日漸增多，礦井深部開采已成為當前煤炭開采的主流[1-2]。在深部開采條件下，高溫、高壓帶來的圍巖劇變、蠕變等特征日益明顯[3-4]，淺埋煤炭支護已經無法滿足礦井的安全生產要求，因此需要對深埋條件下巷道圍巖變形機理進行深入研究，制定有效的巷道圍巖支護形式，實現深部圍巖變形控制[5-6]。國內外眾多學者對深部軟巖巷道進行深入研究，取得重要的研究成果。張國寶[7]等人以常村礦3107 工作面回風巷為工程背景，通過對原支護參數、圍巖變形失穩特征及采動因素分析，提取剝除淺層破碎圍巖后錨網索補強支護等方案，從而實現巷道圍巖的變形控制；高鳳偉[8]等人基于深部開采高應力，復合頂板、大斷面、采動影響等特點提出全斷面高預緊力錨索支護技術，并通過數值模擬和現場工業性實驗等方法，研究確定技術方案等對圍巖變形控制的有效性，減少了巷道的二次返修頻率；王文才[9]等人基于耦合支護理論，提出“錨桿（索）+錨網+注漿”等的支護方案，實現工作面頂底板和兩幫的有效控制。上述研究豐富了深部圍巖控制的內容，但是多注重技術應用的研究，對深部礦井變形的內在機理研究較少，本文以古城煤礦北二2 號回風大巷為研究背景，通過圍巖變形機理研究，確定巷道變形影響因素，為礦井變形控制提供依據。

1 概 況

北二2 號回風大巷布置在3 號煤層中，3 號煤層位于山西組下部，屬穩定型煤層，煤層厚3.35～9.65 m，平均6.05 m，含0.2 m 厚泥巖、炭質泥巖夾矸，煤層平均傾角為0～18°，埋深平均655 m。巷道頂底板巖性如圖1 所示。

2 彈塑性區理論解析

基于彈塑性力學理論，假設半徑為Ro 的圓形巷道，在埋深H≥20 Ro 條件下，巷道處于理想受力狀態，將模型簡化為平面應變問題，忽略巷道圍巖蠕變因素，巷道圍巖變形破壞符合摩爾庫倫模型。依據模型，巷道圍巖由淺入深可分別劃分為破碎圍巖區、塑性圍巖區、彈性圍巖區和原巖應力圍巖區，具體如圖2 所示。基于圖示力學模型分別進行彈性圍巖區和塑性圍巖區的力學及位移數值解析。

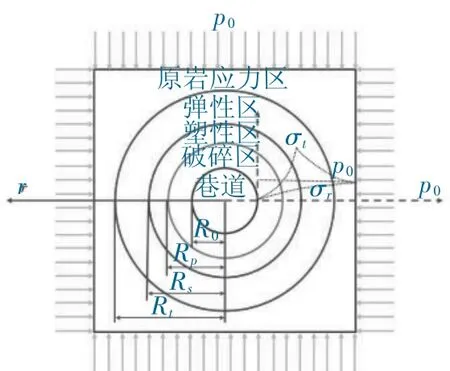
圖2 巷道圍巖力學模型Fig.2 Mechanical model of roadway surrounding rock

2.1 基本方程

極限平衡區靜力平衡方程：

極限平衡條件為：

式中：σt、σr分別為切向應力與徑向應力，MPa：φ為巖體內摩擦角，（°）；C為巖體內聚力，MPa；R 為極限平衡區內所研究點的半徑，m。

將式（2）代入式（1）中，變形整理得到彈性區與塑性區方程。

2.2 彈性區應力方程

徑向應力為：

式中：pO為原巖應力，MPa；pi為支護阻力，MPa：RO為巷道半徑，m；C 為巖體內聚力，MPa；φ為巖體內摩擦角，（°）。

2.3 塑性區應力方程

徑向應力為：

切向應力為：

塑性區半徑為：

周邊位移為：

式中：G 為剪切彈性模量，GPa。

在采動應力影響下，巷道圍巖變形加劇，由于采動應力無法直接量化，但可通過圍巖所受集中應力情況間接反映采動應力變化情況，因此通過施加應力增量，即在原巖應力基礎上增加（1+K）po，則巷道圍巖在采動條件下的Rs和u 分別為：

基于礦壓理論并結合式（4）和式（5）分析，巷道圍巖彈性狀態下受力可由R表示，同時圍巖塑性破壞后，破碎圍巖體內產生的應力變化可由表示。需要注意的是，彈性區范圍內的圍巖變形受到塑性區范圍內破碎巖的抑制，若清理破碎圍巖，則巷道尺寸增加，同時釋放彈性區圍巖變形，增加塑性區的破壞范圍，不利于巷道圍巖的變形控制。

分析式（9）可知，塑性區半徑RS、位移u受到地應力po、支護阻力pi、巖體內摩擦角φ與內聚力C等因素的影響，因此為了進一步研究各個因素的影響程度，故接下來進行不同因素下對巷道塑性區發育狀況的影響研究。

3 不同因素對巷道影響研究

從定量角度出發分析地應力p0、巖體內摩擦角φ、內聚力C與塑性區半徑、周邊位移的關系。當巷道未采取支護措施時，認為pi=0；當巷道采取支護措施時，認為pi≠0，同時針對每個因素進行數值模擬驗證。

3.1 不同埋深對巷道變形影響

巷道圍巖地應力p。通過其巖體的垂直應力體現，而巖體的垂直應力與巷道埋深有直接的關系，通過改變煤層埋藏深度分析地應力對巷道變形程度的影響。北二2 號回風大巷部分范圍處于不穩定圍巖環境，其巷道圍巖主要為泥巖和煤，因此分析不穩定圍巖對確定巷道影響因素十分必要。分析處于100～800 m 埋深條件下的回采巷道塑性區半徑及其周邊位移，為方便計算取pi=0。

在200、400、600、800、1 000 m 等不同埋深條件下進行巷道塑性區模擬，如圖3 所示。

圖3 不同埋深巷道塑性區分布Fig.3 Distribution of plastic zone in roadway with different buried depth

分析圖3 可知，在埋深200～600 m 時，塑性區變化明顯，當埋深大于600 m 后，塑性區變化范圍基本相同，但在局部范圍塑性區有所擴大，同時隨著埋深的增加，巷道當前正在破壞區域逐漸增加，當埋深處于200 m 時，巷道圍巖過去發生破壞而當前未繼續發生破壞，為圖中淺色區域，當埋深增加至400 m 時，深色區域逐漸增加，尤其是巷道中部和兩底角位置，說明當前巷道圍巖不僅過去發生過破壞，當前仍在繼續破壞，當埋深大于600 m時，巷道圍巖基本被深色區域覆蓋，說明當前巷道圍巖極不穩定，而且塑性區有進一步縱深擴展的可能，需要注意的是，在埋深超過800 m 后，巷道淺部圍巖已完全發生破壞，其中頂板和兩底角區域縱深范圍較高，兩幫區域較小。

3.2 不同內摩擦角對巷道變形影響

分析巖體的強度參數內摩擦角φ影響巷道圍巖的變形程度，并分析其對巷道塑性區半徑及周邊位移的影響，取pi=0。

軟巖巖體中，內摩擦角變化較小，設置內摩擦角變化范圍為30°～35°，其他地質參數與上述相同，內聚力取2.0 MPa。本文分別模擬了30°、31°、32°、33°、34°和35°內摩擦角塑性區分布圖，具體如圖4 所示。

圖4 不同內摩擦角下巷道塑性區分布圖Fig.4 Distribution of plastic zone in roadway under different internal friction angles

分析圖4 可知，隨著內摩擦角的逐漸增大，巷道圍巖塑性區范圍逐漸減小，當內摩擦角由30°增加至32°時，巷道淺部圍巖區域變化不大，但頂板深部圍巖塑性區范圍逐漸減小，當內摩擦角繼續增加至33°時，巷道圍巖塑性區范圍明顯減小，其中尤其是淺色表示區域，即過去發生破壞，當前仍繼續發生破壞減小明顯，深色區域，即過去發生破化，當前不再發生破壞，有所增加，當內摩擦角增加至34°時，巷道圍巖范圍持續減小，同時淺色區域基本消失，當內摩擦角繼續增加至35°時，巷道淺部圍巖完整性進一步提高，頂板和兩幫區域破壞范圍較小，但是在底角區域破壞仍較為明顯。

3.3 不同粘聚力對巷道變形影響

分析巖體的強度參數內聚力C共同影響巷道圍巖的變形程度，分析其對巷道塑性區半徑及周邊位移的影響，取pi=0。

軟巖內聚力一般在0～ 5 MPa，基于前述地質參數，取北二2 號回風大巷平均埋深為655 m，巷道半徑4.2 m，巖體容重25 kN/m3，泊松比為0.25，剪切模量為2.35 GPa；內摩擦角為35.14°，本文分別模擬了1、2、3、4、5 MPa 粘聚力塑性區分布圖，具體如圖5 所示。

圖5 不同粘聚力下巷道塑性區分布圖Fig.5 Dstribution of plastic zone in roadway under different cohesion

分析圖5 可知，粘聚力對巷道塑性區發育有一定限制作用，但限制效果不明顯，當粘聚力由1 MPa 增加至4 MPa 時，巷道圍巖塑性區范圍減小不明顯，當粘聚力繼續增加至5 MPa 時，塑性區范圍降低，同時深色區域，過去發生破壞，當前未繼續發生破壞的區域逐漸增加，塑性區未破壞區域擴大，因此，若需要對圍巖塑性區發育進行限制，需要保持粘聚力在較高水平。

綜上所述，基于不同埋深、粘聚力和內摩擦角等不同因素對軟巖巷道影響性分析，確定在埋深一定情況下，增加圍巖粘聚力、內摩擦角度，對巷道塑性區變形都具有一定的控制作用，其中巷道粘聚力以2.5 MPa 為拐點，內摩擦角以33°為拐點，繼續增加后對塑性區控制效果降低。

4 結 論

本文通過理論分析、數值模擬等方法進行深部軟巖巷道圍巖變形機理研究，獲得如下結論。

（1）基于彈塑性力學理論建立圍巖彈性區力學模型，確定塑性區半徑和位移受地應力、支護阻力、圍巖內摩擦角和內聚力等影響。

（2）通過數值模擬確定在埋深確定情況下，粘聚力在2.5 MPa 范圍內和內摩擦角在33°范圍內對巷道塑性區變形有一定控制作用，繼續增加后對塑性區控制效果降低。