面向大區域碳衛星數據的分布式Kriging插值算法優化
周小華,王學志,周園春,孟 珍
(1.中國科學院計算機網絡信息中心,北京 100083;2.中國科學院大學,北京 100049)
1 引言
因碳排放增加導致的全球氣候變暖問題日益突出,正對人類現在及未來的社會經濟活動產生深遠影響。2016年全世界178個締約方共同簽署了《巴黎協定》,呼吁國際社會共同努力將全球溫度上升幅度控制在2 ℃以內。我國也于2020年提出了2030年碳達峰與2060年碳中和的目標[1]。通過碳衛星檢測碳排放的方式具有連續、穩定、大范圍、不受地形限制等優點,為全球各個區域在不同時期的碳排放量化評估提供了重要的技術手段。
近年來,中國、美國、加拿大及日本等國家相繼發射多顆碳衛星,目前仍在軌運行的有OCO-2(美國,2014年)、TANSAT(中國,2016年)、GOSAT-2(日本,2018年)、OCO-3(美國,2018年)、DQ-1(中國,2022年)等[2]。大部分碳衛星基于自身運行軌道以線性散點的形式采集并存儲探測數據,在進行大區域CO2濃度分布量化評估時,需要通過空間插值來彌補缺失區域值。
在上述衛星中,OCO-3衛星時空覆蓋范圍更廣,數據經過嚴格的校準處理,具有更高的測碳精度,且所有數據均可公開訪問,是目前進行全球碳排放檢測與研究的重要數據源[3-5]。因此,本文以OCO-3衛星數據為例進行面向碳衛星數據的Kriging插值算法的優化研究。
2 相關工作
空間插值是指利用周圍已知樣本點基于擬合函數,對未知點的值進行預測的方法。常用的空間插值方法從原理上可分為2大類:確定性方法和地學統計方法。確定性方法基于已知點的相似度或曲面的平滑程度來預測未知點的值,如反距離權重法、徑向基函數插值法等;地學統計方法則通過量化樣本數據點之間的空間自相關性,構造空間結構模型,進而對未知點的值做出預測,如Kriging插值法[6]。
Kriging插值算法可以給出最優線性無偏估計BLUP(Best Linear Unbiased Prediction),在插值時綜合考慮了距離及空間自相關性等因素,具有較高的插值精度[7]。Kriging算法根據前提條件與應用場景的不同又可分為普通Kriging算法、泛Kriging算法、協同Kriging算法及析取Kriging算法等。其中普通Kriging算法是ArcGIS推薦使用的默認插值算法,應用最為廣泛,為此本文將基于普通Kriging算法對OCO-3數據的大區域尺度插值進行研究。
Kriging插值過程比較復雜:在插值前需要計算所有樣本點兩兩之間的距離與協方差,然后擬合得到半變異函數模型,進而對未知點進行插值預測,其中包含矩陣乘積和矩陣求逆等耗時操作。假設有n個數據點和m個未知點,Kriging插值的整體時間復雜度為O(m·n3),在大區域尺度上直接應用Kriging算法進行空間插值計算量很大[8]。
以OCO-3數據為例,覆蓋中國區域的約有150萬個數據點,假設已知樣本點占一半,即75萬個點,僅計算這75萬個點中任意兩點之間的距離與協方差需要約5 000億次運算,基于普通配置的單臺服務器完成上述運算需要30天左右,耗時難以接受。
目前針對Kriging插值算法的并行加速優化方案主要有2種。一種是在高性能計算環境中改造Kriging算法,利用眾核處理器、超高速網絡等硬件優勢對其進行加速。文獻[9,10]在單機多核服務器上采用OpenMP實現了并行Kriging插值;文獻[11-13]基于MPI、MKL等技術結合Cholesky分解法、Gauss-Jordan消元法等矩陣優化算法實現了支持多達512核的并行Kriging插值加速;文獻[14]解決了空間分布不均勻的待插值數據在多核CPU上的負載均衡問題。近年來,隨著GPU核數的不斷攀升以及共享顯存的持續擴大,GPU的并行計算能力已遠超主流CPU的,并在科學計算領域取得了廣泛應用。文獻[15-17]介紹了基于OpenCL、CUDA等技術在GPU上實現并行Kriging插值的方法;文獻[18-20]進一步研究了基于CPU-GPU協同的Kriging并行插值的實現途徑與方法。
以上工作均取得了較高的加速比,顯著提升了Kriging插值效率,但由于對特殊硬件設備及編程環境的依賴,存在使用成本高、開發編程難等問題,而且普遍缺乏容錯機制,水平擴展能力差[21]。
另一種方案是基于目前較成熟的分布式計算框架(如Spark、Hadoop等)在多臺機器上實現Kriging插值的并行加速。分布式計算框架采用計算向數據遷移、分布式內存、懶計算等技術提升海量數據的處理效率,同時具有較強的容錯能力,可在大規模集群上實現快速可靠的并行計算。文獻[22,23]在 Hadoop上實現了分布式Kriging并行插值,與基于CUDA-GPU的方式相比,雖然效率較低,但水平擴展能力強,且具有更好的可靠性和易用性。文獻[24]介紹了基于Spark實現分布式Kriging并行插值的技術方案,并就處理時間、CPU內存利用率等與Hadoop進行了對比,其整體效率達到了Hadoop的5倍左右。以上方案本質上均是基于MapReduce架構對數據分塊然后進行分布式插值,數據分塊一般采用固定空間區域或滑動窗口等方式。固定空間區域會使邊界附近的未知點因近鄰樣本點選擇不全而導致插值結果不準。滑動窗口方式雖然可以在一定程度上避免這一問題,但會因不同子數據塊空間區域重疊而產生大量的重復計算,影響整體計算效率。
文獻[25]將所有待插值數據看作一個整體,優化了Kriging插值過程中的矩陣求逆乘積運算,在Spark上實現了面向大矩陣的分布式Kriging插值。OCO-3數據插值所采用的近鄰點一般不會超過50個,對應矩陣規模較小,求逆乘積等速度非常快,沒必要進行矩陣運算的分布式加速。
此外,OCO-3原始數據按照國家空間站ISS(International Space Station)航線采集,是一種線性時空數據,在通過Kriging插值生成最終的CO2濃度分布數據時,還需要一些特殊的空間操作,如坐標重投影、并行時空檢索、矢量結果柵格化等,而Hadoop、Spark等針對這類空間操作的加速效果并不理想[26]。
本文綜合以上問題,提出另一種方案:將過程復雜、計算量大的Kriging插值過程重構為可多步執行的DAG結構的工作流,并基于具體的數據特征對其中的復雜計算環節進行優化;然后將計算任務進一步拆分,細化插值粒度,形成可在分布式環境下并行執行的計算任務,在底層通過一個雙層架構的分布式工作流調度引擎對拆分后的插值任務進行并行加速。與其他方案相比,本文方案對硬件環境無特殊要求,插值任務調度執行效率高,且架構靈活易實現,可根據空間區域尺度和待插值數據量動態調整集群規模,具有較強的可擴展性。
3 數據統計特征分析
OCO-3衛星數據中包含多項與CO2相關的指標,最常用的是XCO2,即二氧化碳柱濃度,單位為PPM(Parts Per Million volume),其數據覆蓋空間為[-180,-52,180,52],平均采樣分辨率約為2.5 km*2.5 km,采集軌道如圖1所示。

Figure 1 OCO-3 satellite data collection track圖1 OCO-3衛星數據采集軌道
基于Kriging算法對OCO-3數據進行插值包含2個步驟:(1)分析OCO-3數據的統計特征并對其空間相關關系進行建模;(2)基于構建的空間模型進行插值。針對未知點p的插值公式如式(1)所示:
(1)

λ應當是一組使得p點預估值與真實值誤差最小的權重系數,據此構造目標函數f(λ)如式(2)所示:
(2)
將式(1)代入式(2),結合普通Kriging插值的應用條件,使用拉格朗日乘數法可得λ的求解公式[27],如式(3)所示。
(3)
其中,rij是基于距離求得的半變異函數值;樣本點個數n由樣本點密度與半變異函數模型決定,通常控制在20~100內,太少會使部分相關性強的點不能參與插值,太多會讓過多無關點參與插值,二者都會導致插值結果不準。
半變異函數模型基于近鄰樣本點的距離與協方差通過最小二乘法擬合得到。常見的半變異函數模型有球形模型、圓形模型、指數模型、高斯模型及線性模型等。本文隨機選取100個樣本點,并分別計算與其相鄰的500個數據點的距離與協方差,然后以5 km為區間計算協方差的平均值,得到各個樣本點對線性模型的擬合度分布,如圖2所示。
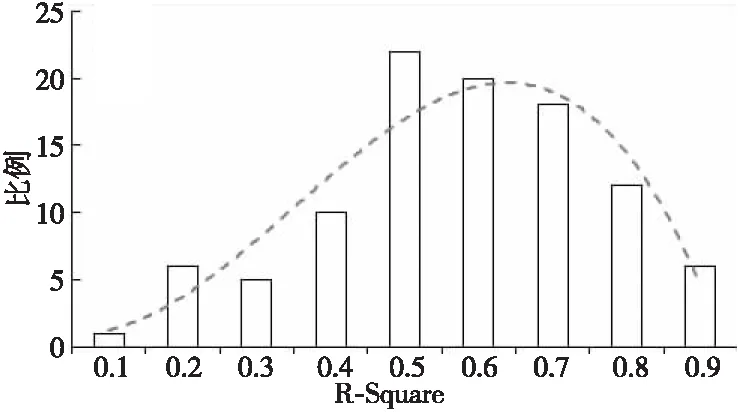
Figure 2 Distribution of linear model fitting圖2 線性模型的擬合度分布
由圖2可知,擬合度超過0.5的數據點占比接近80%,因此本文選取線性模型作為OCO-3數據的插值函數模型。
4 整體概述
基于以上分析,本文設計并實現如圖3所示的分布式Kriging插值加速框架。該框架以用戶指定的時空范圍及目標分辨率為輸入,輸出結果為柵格化的XCO2濃度分布影像,插值過程分為2個階段:Kriging插值工作流構建和工作流任務的分布式并行加速。在工作流構建階段,將串行的Kriging插值過程細化拆分為多個相對獨立的任務模塊,并根據其輸入輸出的依賴關系確定不同任務的執行時序;然后根據數據特征與計算模式將每個獨立的任務模塊進一步拆分為可并行執行的子任務;最后由底層面向DAG工作流的分布式調度引擎負責加速執行。

Figure 3 Distributed Kriging interpolation framework for OCO-3 data圖3 面向OCO-3數據的分布式Kriging插值框架
底層的分布式調度引擎基于管理與計算分離的雙層架構實現。第1層主要負責控制整個工作流任務按序向前推進。第2層負責工作流中具體子任務在分布式環境中的調度執行。
基于上述結構劃分,下文將首先介紹Kriging插值工作流的構建細節及其中關鍵步驟的優化方法;然后介紹如何將Kriging插值工作流轉換為可在分布式環境中并行執行的任務以及面向該任務的分布式調度引擎的設計與實現。
5 插值工作流的構建與優化
結合OCO-3衛星數據特征構建Kriging插值工作流,如圖4所示。
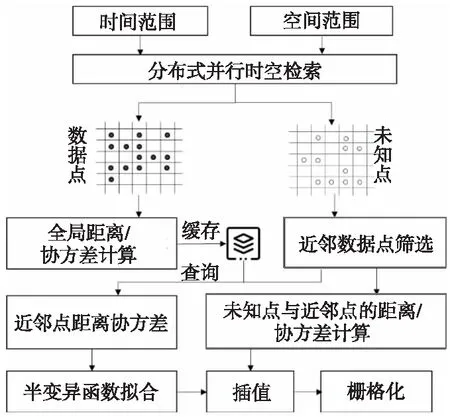
Figure 4 Workflow of Kriging interpolation for large region圖4 面向大區域尺度的Kriging插值工作流
整個工作流包含3個主要模塊:(1) 數據解析處理:通過時空檢索得到指定時空范圍內的原始線性排列的散點數據,將其網格化,然后計算并緩存所有數據網格之間的距離與協方差;(2) 網格遍歷插值:逐個遍歷所有未知網格,基于其近鄰網格之間的距離與協方差擬合半變異函數模型,以此對未知網格進行插值;(3) 插值結果匯總:整合所有數據網格與插值網格,結合空間位置信息,將其柵格化為XCO2濃度分布影像。
在上述工作流中,時空檢索、近鄰點篩選以及全局距離協方差計算是比較耗時的3個環節,為此本文基于網格剖分、數據分鏈等方式對其進行了有針對性的優化,使整體插值效率得到顯著提升,具體優化細節如下文所述。
5.1 分布式并行時空檢索
直接基于大尺度不規則的空間區域進行檢索十分耗時,為此,本文在對原始OCO-3數據點構建空間索引(RTree)的基礎上,進一步將空間檢索范圍由中心點進行遞歸網格化拆分,將單個不規則大區域的空間相交查詢轉換為多個矩形網格的并行相交查詢。算法偽代碼如算法1所示。
算法1基于網格的并行時空檢索算法
輸入:最小網格G(w,h),空間查詢范圍R。
輸出:與R相交的OCO-3數據點集合RST。
//計算R的外包矩形
x0,x1=min(R.coords[:,0]),max(R.coords[:,0]);
y0,y1=min(R.coords[:,1]),max(R.coords[:,1]);
//調整外包矩形使其為G的整數倍
a,b,c,d=align(x0,y0,x1,y1);
grids=[[a,b,c,d]];
G1=[];//位于R內部的網格
G2=[];//位于R邊界的網格
whilenotgrids.empty():
g=grids.pop();
ifR.contains(g)://g位于R內部
G1.append(g);
elseifR.intersects(g)://g位于R邊界
ifg.area()≤Smin:
G2.append(g);
else:
//以G為單位將g近似等分為4個子網格
subgrids=quad_split(g,G);
forsginsubgrids:
grids.append(sg);
endfor
endif
endif
endif
endwhile
rst1=parallel(query_by_extent,G1);
rst2=parallel(query_by_intersect,G2);
RST=merge(rst1,rst2);
returnRST;
算法1中的query_by_extent通過直接比較數值大小的方式獲得目標數據,query_by_intersect則先通過數值比較的方式快速縮小搜索空間,然后通過精確空間相交判斷獲得目標數據。parallel是將以上2個函數分布到不同服務器節點并行執行的方法。
圖5是基于以上算法對新疆省邊界進行網格化拆分后的效果。
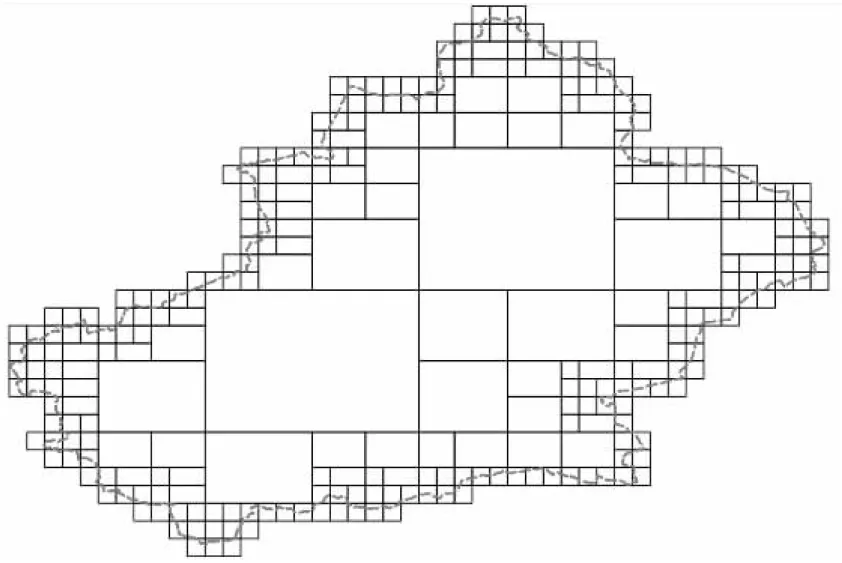
Figure 5 Illustration of grid dividing of spatial range圖5 空間范圍網格拆分示意圖
對空間區域網格化后,所有網格都可獨立地由不同節點上的計算進程進行查詢。大部分數據可以基于內部少量大網格通過query_by_extent快速查詢得到,剩余數據則基于邊界小網格通過query_by_intersect查詢得到,小網格雖然數量多,但網格面積大大縮小,查詢速度也有顯著提升。
采用上述方法分別檢索中國大陸、新疆、陜西及北京等4個不同大小區域的OCO-3數據,與直接基于單個大區域的查詢方式的耗時對比如表1所示。
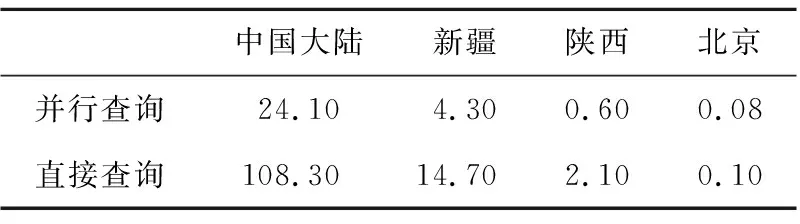
Table 1 Comparison of spatial retrieval time in different regions表1 不同區域尺度的空間檢索耗時對比 s
由表1可知,上述基于網格拆分的并行時空檢索優化方法可以顯著提升檢索效率,且空間范圍越大,速度優勢越明顯。
檢索到原始數據后按照目標分辨率對其進行網格化處理:取處于同一個網格的所有樣本點的均值作為該網格的XCO2值,網格位置用中心點表示,同時對所有網格按照行列進行編號。網格編號規則如式(4)所示:


(4)
其中,gm為行編號;gn為列編號;(px,py)為網格的中心點坐標;dt為用戶指定的分辨率,即網格邊長。
5.2 近鄰數據點篩選
KDTree是常用的近鄰數據點篩選方法,但其在查詢時,每次都要回溯到根節點,且效率會隨著樣本數據量的增加大幅下降。另一種思路是基于空間填充曲線將待索引空間分為多級網格,并對每個網格賦予一個帶有位置信息的編號,進而將二維空間的坐標點映射到一維空間,基于該特性可以快速得到處于同一空間區域的數據點。GeoHash、Google S2等都是基于該思路的空間索引算法,空間填充曲線雖然在一維空間里盡可能地維持了空間本地性,但仍有一定的”跳躍”,即部分編號相鄰的網格實際相距較遠,直接通過編號前綴獲得的候選節點并不全部準確。
考慮到OCO-3樣本數據網格化后分布比較均勻,本文設計并實現了更快的近鄰搜索算法,如圖6所示。

Figure 6 Illustration of neighbor search based on grids圖6 網格化近鄰搜索示意圖
圖6中,gx為待插值網格,網格編號為(rx,cy);sr為近鄰搜索的最大距離;dt為網格邊長;ceil為向上取整函數;floor為向下取整函數。在圓形區域內部及邊界的數據網格即為所求近鄰數據網格,具體篩選步驟如下:
(1)計算圓形區域的外包矩形范圍:Ro= [ox0,oy0,ox1,oy1],計算公式見圖6;
(2)計算圓形區域的內接正方形范圍:Ri=[ix0,iy0,ix1,iy1],計算公式見圖6,該范圍內的所有數據網格均為待插值點的近鄰數據網格;
(3)逐個遍歷介于Ro與Ri之間的數據網格,篩選出所有與gx距離小于sr的網格;
(4)匯總步驟(2)與(3)的結果,即為gx的所有近鄰數據網格。
步驟(1)通過外包矩形快速鎖定一個較小的候選網格范圍。步驟(2)則通過內接矩形直接確定了大部分近鄰數據網格。以上2個步驟都是基于簡單的公式計算完成,時間復雜度為O(1)。介于Ro與Ri之間的數據網格需要逐個遍歷,但數量較小,不會對整體耗時產生明顯影響。
5.3 全局距離協方差計算
Kriging插值的核心步驟是計算未知點近鄰數據網格兩兩之間的距離和協方差,進而以此擬合得到用于插值的半變異函數模型。由于相鄰未知網格的近鄰數據網格重疊度較高,本文采用預先計算并緩存的方式來避免重疊區域的重復計算。此外,考慮到插值只用近鄰數據,為此在執行計算時,只采用一定范圍內的數據網格,范圍大小由目標分辨率與數據分布特征確定。
直接計算所有數據網格兩兩之間的距離與協方差計算量太大(如圖7a所示),耗時無法接受,而且由于交叉太多,難以并行加速。分塊計算再合并的方式(如圖7b所示)可以實現并行加速,但合并過程比較復雜,且難以應用距離限制計算量。針對以上問題,本文采用如圖8所示的分行鏈式結構對數據進行重新組織,以實現分布式環境下的全局距離與協方差的并行計算。
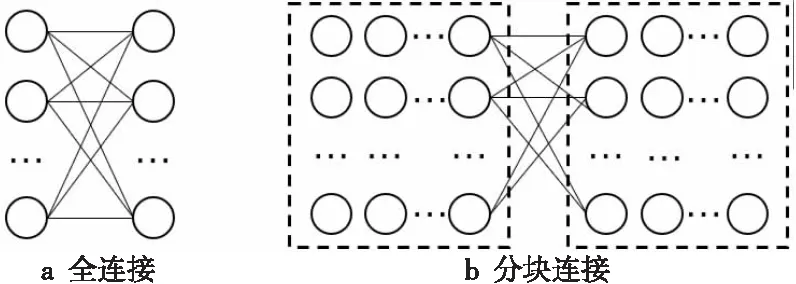
Figure 7 Two modes of global distance and covariance computation圖7 2種全局距離協方差計算模式

Figure 8 Linked structure of data samples圖8 樣本數據點的鏈式組織結構
圖8中,xn表示數據網格的橫坐標,y(n,i)表示數據網格的縱坐標,v(n,i)為XCO2值。距離基于位置(xn,y(n,i))計算,協方差基于v(n,i)計算,采用當前行向右,跨行由中間向兩側的遍歷策略進行計算(如圖9所示)。算法偽代碼如算法2所示。

Figure 9 Illustration of distance and covariance computation between neighbor data points圖9 相鄰數據點距離協方差計算示意圖
算法2相鄰數據網格距離協方差計算
輸入:行列號為(M,N)的數據網格G。
輸出:相鄰數據網格之間的距離與協方差字典DVS。
forginnext(M,N)://行內向右遍歷
//距離、協方差計算
d,v=dist(g,G),cov(g,G);
ifd>MAXDIST:
break;
endif
DVS[(G,g)]=(d,v);
endfor
m,n=G.M+1,G.N;//開始逐行向下遍歷
whilem forginnext(m,n)://行內向右遍歷 d,v=dist(g,G),cov(g,G); ifd>MAXDIST: break; endif DVS[(G,g)]=(d,v); endfor forginpre(m,n)://行內向左遍歷 d,v=dist(g,G),cov(g,G); ifd>MAXDIST: break; endif DVS[(G,g)]=(d,v); endfor m+=1; endwhile 其中,MAXDIST為限定相鄰網格的距離常量,根據待插值區域的樣本點分布設置;DVS的主鍵為(m0,n0,m1,n1),m,n為數據網格編號,且滿足:(m0 本節介紹如何將上述Kriging插值工作流以及優化算法轉換為可并行執行的任務模塊,并基于不同任務模塊之間輸入輸出的依賴關系確定調度執行的順序,最后通過一套雙層架構的分布式調度引擎實現上述工作流任務的并行加速。 整個工作流分為5個主任務:并行時空檢索(T1)、全局距離/協方差計算(T2)、近鄰點篩選(T3)、半變異函數擬合并插值(T4)和插值結果柵格化(T5),如圖10所示。 Figure 10 Kriging interpolation workflow for distributed environment圖10 面向分布式環境的Kriging插值工作流 主任務T1基于時間范圍區間劃分及空間范圍網格化拆分為m個可分布式并行執行的子任務,T1的輸出結果為網格化的數據點。主任務T2以T1的輸出作為輸入,基于分行鏈式存儲結構拆分為n個可分布式并行執行子任務,T2的結果以鍵值對的形式緩存至Redis內存數據庫。主任務T3并行遍歷待插值網格,基于5.2節描述的算法獲取每個待插值網格的近鄰數據網格集合。主任務T4以該近鄰數據網格集合以及Redis緩存為輸入完成最終的半邊異函數擬合與插值,T4的輸出結果最終通過主任務T5柵格化為GeoTIFF文件進行存儲。主任務的執行時序如圖11所示。 Figure 11 Executing sequence of main tasks圖11 主任務執行時序 圖11中,主任務T2、T3為并行執行,其他主任務均為串行執行,執行到具體某個主任務時,主任務內部的子任務可通過獨立調度在分布式環境下并行執行。 基于6.1節所述的工作流任務特點,本文設計并實現如圖12所示的雙層任務調度框架。第1層為唯一的主調度器,負責主任務的調度管理與時序控制;第2層包含多個分調度器,每個分調度器管理一個或多個計算節點,并具體負責子任務的調度執行,分調度器由主調度器管理,接受并執行主調度器發送過來的調度命令并向其匯報自己的狀態。 Figure 12 Framework of double-tier scheduling engine for Kriging interpolation workflow圖12 面向Kriging插值工作流的雙層任務調度框架 所有主任務按照依賴關系與執行順序生成一個DAG結構的任務流,其任務節點以任務記錄的形式存入主任務隊列。任務記錄中包含任務標識(id)、前序任務(pre)、后續任務(next)、狀態(status)、輸入(input)、輸出(output)、執行時間(timestamp)等信息。主調度器遍歷該任務隊列,取出所有滿足條件(無前序依賴,且輸入條件已滿足)的主任務交給分調度器執行,分調度器將主任務對應的子任務通過分布式任務調度引擎將其分發到計算集群上并行執行,并實時監控其運行狀態。當前主任務執行結束后,分調度器向主調度器匯報,主調度器據此更新主任務隊列中相關的任務狀態、前序依賴、輸入輸出等信息,并繼續調度執行符合條件的主任務。 為了實現任務狀態快速更新,降低任務調度開銷,主調度器與分調度器均采用C++開發實現,并對圖10所示的工作流進行拓撲排序形成任務隊列,然后將其以鍵值對的形式存儲至有序字典中。其中key為任務標識,value為包含執行該任務的函數名稱、參數以及前后任務等信息。 位于底層計算節點的任務執行模塊基于Dask實現。Dask打破了Python中GIL(Global Interpreter Lock)的限制,支持多核并行計算與核外計算,且具有不亞于OpenBLAS的矩陣運算效率[28]。 考慮到OCO-3樣本點總數量在10億以內,內存占用不超過50 GB,為了提升數據訪問效率,不同計算節點之間的數據共享通過內存數據庫Redis實現。 分調度器在執行任務分配時,優先將同一主任務的子任務分配到相同計算節點上,以盡可能降低任務調度管理以及跨節點數據傳輸等帶來的額外開銷。計算節點根據自身可用的計算資源設置任務并發數上限,當某個節點負載接近上限時,再由分調度器將待執行任務分配到其他節點。 在上述框架中,主調度器、分調度器與任務執行等各模塊相對獨立,各個模塊之間的任務調度、運行狀態、啟停命令等消息傳遞則基于ProtoBuf序列化協議實現,該協議與XML、JSON相比,序列化速度更快、數據體積更小[29]。 根據處理級別與數據內容的不同,OCO-3衛星數據產品分為18種類型。其中,OCO3_L2_Standard V10r為官方推薦數據集,自2019/08/05持續更新至今。截至2021/12/31,已發布了11 380個數據文件,共包含109 315 194數據點,發布的數據產品采用NetCDF-4/HDF5格式存儲。為方便后續分析,本文將原始數據中的時間、位置、XCO2等信息以四元組(timestamp,longitude,latitude,xco2)形式進行重新組織,重組后的數據存入關系型數據庫PostgreSQL中。 為測試和評估本文所提出的優化算法與計算框架的性能效率,選取了2021年的OCO-3數據進行實驗分析,測試環境為6臺相同配置(如表2所示)的服務器搭建的集群,服務器之間的網絡帶寬為1 Gbps。其中,5臺服務器用于搭建計算集群,每臺服務器的計算任務并發上限數為16,另外1臺用作Redis數據庫服務器,所有服務器掛載均基于MooseFS搭建的分布式文件系統。 為測試不同區域尺度下的插值效率,本文選取了中國大陸、新疆、陜西、北京等4個邊界不規則且大小不同的測試區域,如圖13所示。 Figure 13 Interpolation regions of different sizes圖13 不同大小的插值區域 基于5.1節介紹的并行時空檢索方法得到以上4個區域的原始數據后,按0.1度分辨率對原始樣本點數據進行網格化,并取平均值作為該網格的XCO2數值。以上4個區域包含的原始樣本數據點個數、數據網格數、未知網格數如表3所示。 Table 3 Size of test data表3 測試數據量 由表3可知,OCO-3數據在不同區域的分布并不均勻,新疆的數據覆蓋比例比陜西的高20%左右,以上4個區域的數據分布情況如圖14所示。 Figure 14 Data coverage of 4 different regions圖14 4個不同區域的數據覆蓋情況 Figure 15 Images rendered from interpolation results of four regions圖15 4個區域的插值結果渲染圖 基于上述環境,采用本文所述方法框架得到的插值結果如圖15所示。完成以上4個區域插值的整體耗時如圖16所示。 Figure 16 Comparison of time consumed by interpolation in four different regions圖16 4個不同區域的插值耗時對比 由圖16可知,雖然陜西與北京的面積、待插值數據量相差20倍左右,但耗時僅相差3倍左右,數據量的增加并未導致耗時等比例增加。主要是因為北京區域的數據規模較小,插值時不能完全利用已有的計算資源,當有少量的數據增加時,更多未被利用的資源開始參與計算,因此陜西相對北京的插值耗時增加不明顯。但是,當網格數據量增加到15 638且待插值網格達到2 368時,單臺服務器的計算資源已難以支撐,更多的計算節點開始參與插值,耗時顯著增加,但增加幅度仍遠小于數據量的增長幅度。當區域尺度由新疆擴大到全國時,網格數據量增加了4倍左右,待插值網格增加了10倍左右,但耗時僅增加了5倍左右,說明本文所設計的方法框架針對大區域尺度的插值具有良好的并行加速效果。 以上4個地區在不同任務階段的耗時對比如圖17所示。4個區域最終的柵格化(T5)都沒有超過0.1 s,與其他階段耗時差異太大,故未在圖17上展示該階段的耗時。由圖17可知,4個階段耗時最多的是T2階段,該階段需要計算相鄰數據點兩兩之間的距離和協方差并緩存至Redis,時間復雜度約為O(n2),計算量大且有較多的I/O開銷;T3與T4階段主要操作對象為待插值網格,其數量少于數據網格,且其中近鄰篩選與插值可以通過簡單計算或緩存查詢直接完成,時間復雜度約為O(n),因此耗時均小于相同區域的T2階段的。 Figure 17 Comparison of time consumed at different stages in four test regions圖17 4個測試區域在不同階段的耗時對比 本文選取Spark作為對比框架。Spark是一種基于分布式內存的大數據分析處理框架,支持交互式的數據查詢與大批量任務的并行執行,GeoSpark對Spark進行了擴展,使其具有了大規模時空數據處理能力[30]。圖18展示了GeoSpark與本文所用網格化方法在時空數據檢索階段(T1)的效率對比。由圖18可知,本文所采用的方法在4個區域上的檢索效率均高于GeoSpark的,而且區域越大,本文所述方法的效率優勢越明顯。 Figure 18 Comparison of time consumed between GeoSpark and the proposed method圖18 GeoSpark與本文并行時空檢索方法耗時對比 考慮到基于矩陣的批量插值模式需要大內存的支持且不適合不規則的大區域,所以基于Spark的插值依然采用先計算距離/協方差并緩存然后逐點插值的流程。全局距離/協方差計算(T2)、近鄰點篩選(T3)和半變異函數擬合并插值(T4)3個階段在Spark上的實現方式如圖19所示。 Figure 19 Flow of Kriging interpolation based on Spark圖19 基于Spark的Kriging插值流程 Spark主要通過數據分區后獨立并行計算來提升計算效率,而距離/協方差計算需要大量交叉運算,難以直接分成獨立的數據塊。為此在計算之前,本文將所有數據網格通過兩兩組合的形式形成圖19b所示的四元組;然后再由Spark進行并行計算,后續的近鄰查詢、半變異函數擬合與插值仍采用本文所述的方法,具體的子任務由Spark負責調度執行。基于Spark完成以上操作的耗時如圖20所示。 Figure 20 Comparison of time consumed between Spark and the proposed method圖20 本文方法與Spark插值耗時對比 由圖20可知,在大區域尺度上,本文方法相對Spark具有明顯的效率優勢,原因主要有2個:(1)在計算距離協方差時,本文采用的分行鏈式存儲結構可以有效地結合距離范圍限制參與計算的數據量,而Spark的分塊計算模式難以利用該條件;(2)在后續Kriging插值階段,Spark自身的內存計算、彈性數據集等技術難以對逐點插值的計算流程進行加速,而其內部復雜的任務調度、監控等操作增加了任務之外的額外開銷。 碳衛星數據是進行碳排放和碳追蹤研究的重要數據源,但在大區域尺度上基于Kriging算法進行插值時計算量很大,而且難以直接進行并行加速。為此,本文以常用OCO-3衛星數據為例,設計了一種DAG結構的Kriging插值工作流,并實現了可對其并行加速的雙層分布式調度引擎,通過調整插值過程、細化插值粒度以及優化其中的近鄰查詢、距離/協方差計算等關鍵環節使該工作流可以在分布式環境下快速執行。實驗結果表明,本文方法框架可以高效完成不同區域尺度上的OCO-3快速插值,在大區域尺度上,相對Spark也具有明顯的速度優勢。后續將進一步探索更多碳衛星觀測數據,研究不同碳衛星數據的融合方法,形成一套更加準確高效的碳衛星觀測數據插值融合框架。6 插值任務的分布式并行加速
6.1 工作流任務模塊劃分


6.2 分布式調度執行與時序控制
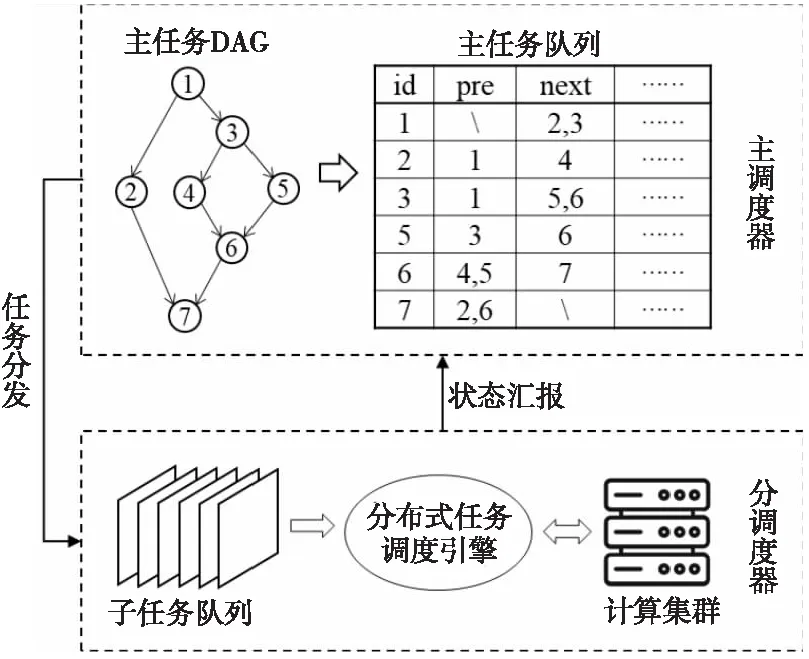
7 實驗與結果分析









8 結束語

